VP记录:Codeforces Round 865 (Div. 2) A~C
传送门:CF
难受了,本来想写到D题的,但是D题是一道交互题,只能作罢,提前润了
A题:A. Ian Visits Mary
简单的数学题,发现只要控制矩阵的宽为1就不可能在途中经过格点,直接实现即可(具体看代码)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {int T=read();while(T--) {int a=read(),b=read();cout<<2<<endl;cout<<a-1<<" "<<1<<endl;cout<<a<<" "<<b<<endl;}return 0;
}
B题:B. Grid Reconstruction
一道构造题.需要找一下性质.
首先发现首尾必然应该放最大的两个数字,也就是2n,2n-1,原因显然.
我们需要让最小值最大.观察一下样例以及优美的平均思想,不难发现我们只需将所有的 2 ∗ k − 1 , 2 ∗ k 2*k-1,2*k 2∗k−1,2∗k填在斜对角即可(并且一大一小的进行填),举个栗子,也就是:
10 1 7 3 5
2 8 4 6 9
为什么这样干是正确的呢,首先我们显然需要将小的数填在减的位置,然后将大的数字放在加的位置,这样才能保证最大.所以我们一大一小的进行填.
假设现在我们现在处于1的位置,我们有两个选择,可以走右边,也可以走下面,诶,此时我们发现走右边比走下面小加了一个1,但是我们此时又会发现走右边的话接下来走3又会少减了1,这样就平均了.这个证明可能不太严谨,但是这就是平均的优美之处!!,严谨证明应该也不难证明,但是限于篇幅此处暂略(\doge)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x = 0, w = 1;char ch = getchar();for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') w = -1;for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';return x * w;
}
#define maxn 1000000
const double eps = 1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int ans[3][maxn];
int main() {int T = read();while (T--) {int n = read();ans[1][1]=2*n;ans[2][n]=2*n-1;int l=1,r=2*n-3;for(int j=2;j<=n;j++) {if(j&1) {ans[1][j]=r;r-=2;}else {ans[1][j]=l;l+=2;}}l=2,r=2*n-2;for(int j=1;j<=n-1;j++) {if(j&1) {ans[2][j]=l;l+=2;}else {ans[2][j]=r;r-=2;}}for(int i=1;i<=2;i++) {for(int j=1;j<=n;j++) {printf("%d ",ans[i][j]);ans[i][j]=0;}printf("\n");}}return 0;
}
C题:C. Ian and Array Sorting
诶,又是一道大胆猜测的题目.
我们可以将连续的两个数加一或者减一.简单把玩一下就会发现存在这样的一个性质.假设我们有三个数 a , b , c a,b,c a,b,c连续,我们可以将 a − 1 , c + 1 a-1,c+1 a−1,c+1或者 a + 1 , c − 1 a+1,c-1 a+1,c−1这两种操作是由尚需操作转化而来的,证明显然.
我们需要将原来的序列转化成一个不下降的序列,贪心的来想就需要将前面的数字改的小一点就行,也就是对于每一位数字来说,我们都要在满足大于其前面的所有数字的前提下尽量的变得更小.诶,此时我们大胆猜测,我们直接使用上述两种操作,将前面的数字都改为 0 0 0(当然可以是任意一个数,不一定为0).也就是对于第 i i i位来讲,假设对于第 i i i位之前的所有数字我们都是0,我们此时将 a [ i ] a[i] a[i]也变为0,将差值使用前面的转化方法加到 a [ i + 2 ] a[i+2] a[i+2]上.这样的话,我们最终数列就变成了这样的一个数列,前 n − 2 n-2 n−2项都是0,最后两项是所有的奇数项之和以及所有的偶数项之和.所以此时只需要判断这两个数即可.因为对于相邻的两个数来说我们并不能改变他们的差值(仅当n为偶数时).
但是对于n为奇数的情况就不同了,我们可以将前 n − 1 n-1 n−1同时减小,这样就可以小于最后一个数了.也就是对于n为奇数的时候必然是满足题意的.
赛场上直接猜就完了,但是写博客不就是为了让别人知道为什么这样做是对的吗,所以此处简单证明一下:
基于上述的结论,考虑使用反证法来证明当n为偶数时,当前仅当所有奇数位和<=偶数位和时有解.那么假设当n为偶数时,当前仅当所有奇数位和>偶数位和时依旧存在解.为了方便起见将最终满足题意的奇数位记为 a 1 , a 2 , a 3 , a 4.... a k a1,a2,a3,a4....ak a1,a2,a3,a4....ak,偶数位记为 b 1 , b 2 , b 3... b k b1,b2,b3...bk b1,b2,b3...bk
并且我们此时有 ∑ a i > = ∑ b i \sum{a_i}>=\sum{b_i} ∑ai>=∑bi,根据题意还应该有:
a 1 < = b 1 < = a 2 < = b 2 < = . . . < = a k < = b k a1<=b1<=a2<=b2<=...<=ak<=bk a1<=b1<=a2<=b2<=...<=ak<=bk,显然我们会发现 ∑ a i < = ∑ b i \sum{a_i}<=\sum{b_i} ∑ai<=∑bi,与已知矛盾.所以证毕.
上述证明了必要性,至于充分性应该显然,此处就不在赘述了.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
signed main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) {a[i]=read();}if(n&1) {puts("YES");continue;}int sum1=0,sum2=0;for(int i=1;i<=n;i++) {if(i&1) sum1+=a[i];else sum2+=a[i];}if(sum1<=sum2) puts("YES");else puts("NO");}return 0;
}
相关文章:
 A~C)
VP记录:Codeforces Round 865 (Div. 2) A~C
传送门:CF 难受了,本来想写到D题的,但是D题是一道交互题,只能作罢,提前润了 A题:A. Ian Visits Mary 简单的数学题,发现只要控制矩阵的宽为1就不可能在途中经过格点,直接实现即可(具体看代码) #include <bits/stdc.h> using namespace std; typedef long long ll; #de…...

智能学习 | MATLAB实现PSO-SVM多输入单输出回归预测(粒子群算法优化支持向量机)
智能学习 | MATLAB实现PSO-SVM多输入单输出回归预测(粒子群算法优化支持向量机) 目录 智能学习 | MATLAB实现PSO-SVM多输入单输出回归预测(粒子群算法优化支持向量机)预测效果基本介绍模型原理程序设计参考资料预测效果 基本介绍 MATLAB实现PSO-SVM多输入单输出回归预测(粒…...
Java后端:html转pdf实战笔记
目录 1、htmltopdf有什么用? 2、什么是wkhtmltopdf 3、wkhtmltopdf 参数介绍 4、示例项目 5、预览效果 1、htmltopdf有什么用? htmltopdf 是一款基于wkhtmltopdf技术的html转pdf文档java类库,支持html转pdf和url转pdf。 2、什么是wkhtmltopdf…...

设计模式-适配器模式
适配器模式 文章目录 适配器模式1、什么是适配器模式2、为什么要用适配器模式2.1、封装有缺陷的接口设计2.2、统一多个类的接口设计2.3、替换依赖的外部系统2.4、兼容老版本接口2.5、适配不同格式的数据 3、如何使用适配器模式1、类适配器2、对象适配器 总结 1、什么是适配器模…...
一款支持全文检索、工作流审批、知识图谱的企事业知识库
一、项目介绍 一款全源码,可二开,可基于云部署、私有部署的企业级知识库云平台,一款让企业知识变为实打实的数字财富的系统,应用在需要进行文档整理、分类、归集、检索、分析的场景。 获取方式q:262086839 为什么建立知识库平台&…...
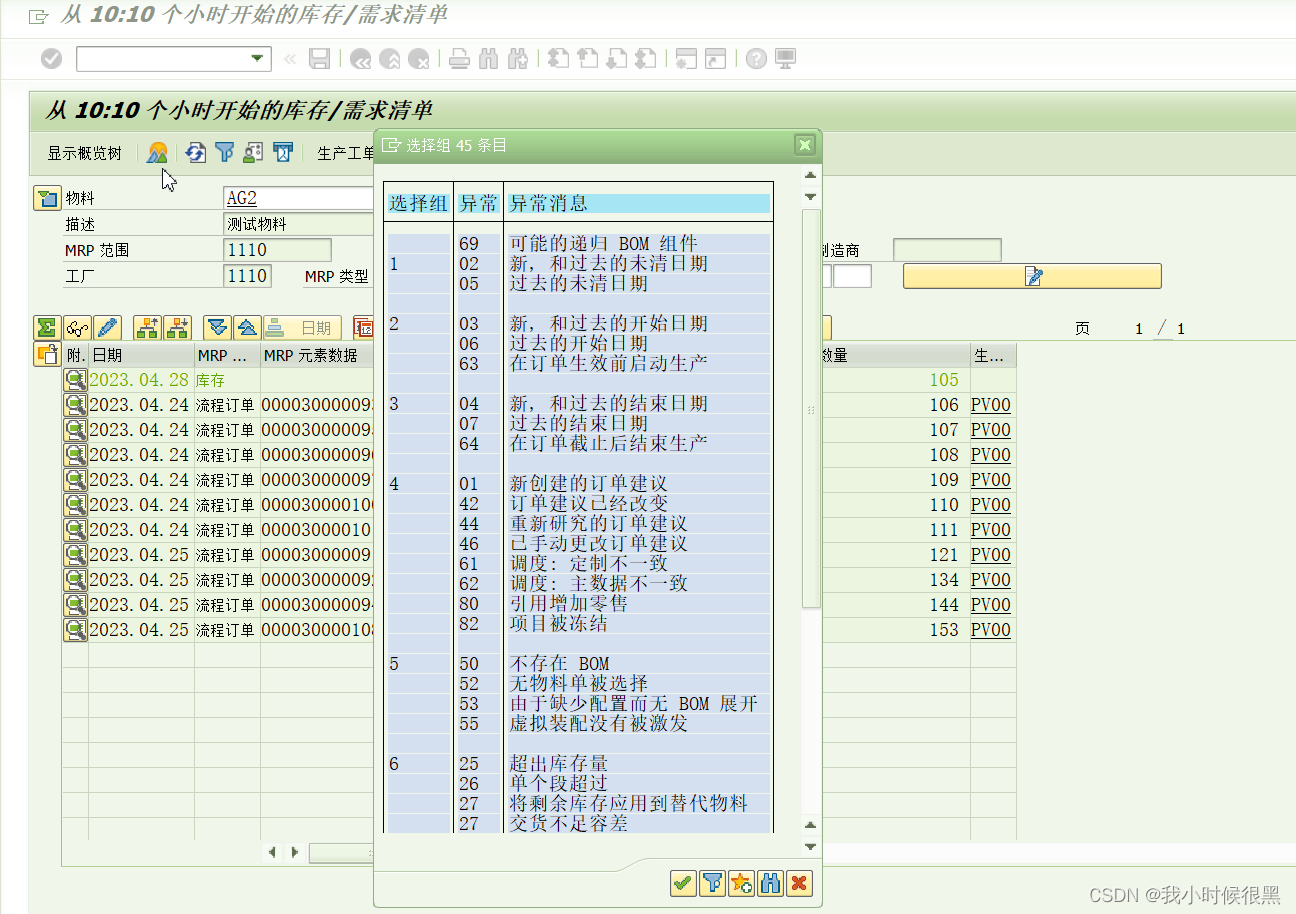
SAP MRP例外信息解释
SAP中MRP的例外信息,一共分为八类,下面是所有例外信息的解释 第一类: 69:BOM组件可能是递归的,即自己的子集中包括了自己。 02:订单创建日期在过去,可能是没有及时处理,这个建议表…...

广义的S变换
广义的S变换 S变换中窗函数是高斯函数 1 2 π σ e − 1 2 σ t 2 \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{1}{{2\sigma }}{t^2}}} 2π σ1e−2σ1t2,它的形状由方差 σ 1 f \sigma\frac{1}{f} σf1控制。许多研究表明,S变换中窗函数的…...

python异常及其捕获
文章目录 异常的捕获异常是可传递的 异常的捕获 1.为什么要捕获异常? 在可能发生异常的地方,进行捕获。当异常出现的时候,提供解决方式,而不是任由其导致程序无法运行。 2.捕获异常的语法? try: 可能要发生异常的语句 except 异常名 as 别…...

mysql实现存在则保存,不存在则更新
方式1 ON DUPLICATE KEY UPDATE 使用前提:表必须配置唯一键或者主键,且保存的字段中包含该键【重点】 原理: ON DUPLICATE KEY UPDATE如果配合主键,存在数据a,新插入b,如果主键不冲突,会保存b…...
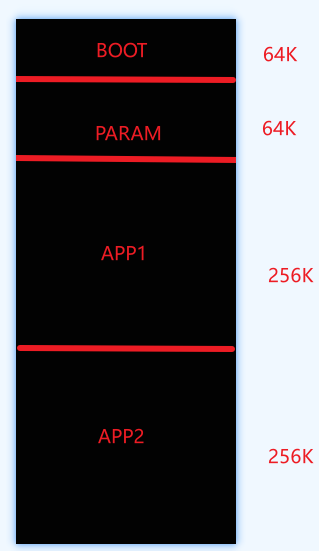
MCU固件升级系列1(STM32)
本系列将从升级流程、boot代码编写、APP代码编写以及固件打包来介绍,硬件选用STM32F407ZGT6(手里只有),来完成这系列教程。 前言 为什么需要固件升级: 功能更新:随着产品的迭代和用户需求的变化,可能需要…...
)
ImageJ 用户手册——第五部分(菜单命令Window)
. 菜单命令32. Window32.1 Show All32.2 Put Behind32.3 Cascade32.4 Tile 33. Help33.1 ImageJ Website33.2 ImageJ News33.3 Documentation33.4 Installation33.5 Mailing List33.6 Dev. Resources33.7 Plugins33.8 Macros33.9 Macro Functions33.10 Update ImageJ33.11 Refr…...

利用css实现视差滚动和抖动效果
背景: 前端的设计效果,越来越炫酷,而这些炫酷的效果,利用css3的动画效果和js就可以实现,简单的代码就能实现非常炫酷的效果。 原理: 利用 js监控scrollTop的位置,通过 top定位图片的位置&#x…...
)
以桨为楫 修己度人(一)
目录 1.人工智能开创的新时代 2.使命开启飞桨一春独占 3.技术突破奠定飞桨品牌一骑绝尘 4.行业应用积淀飞桨品牌一枝独秀 5.生态传播造就飞桨品牌一众独妍 6.深度学习平台的现状和未来思考 7月28日,2022全球数字经济大会“人工智能驱动未来产业论坛”在京召开&…...
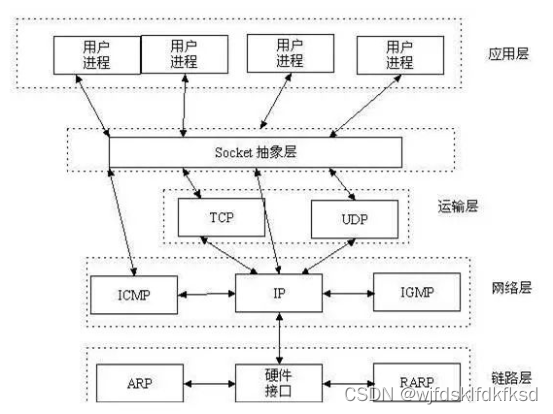
网络编程之简单socket通信
一.什么是Socket? Socket,又叫套接字,是在应用层和传输层的一个抽象层。它把TCP/IP层复杂的操作抽象为几个简单的接口供应用层调用以实现进程在网络中通信。 socket分为流socket和数据报socket,分别基于tcp和udp实现。 SOCK_STREAM 有以下…...
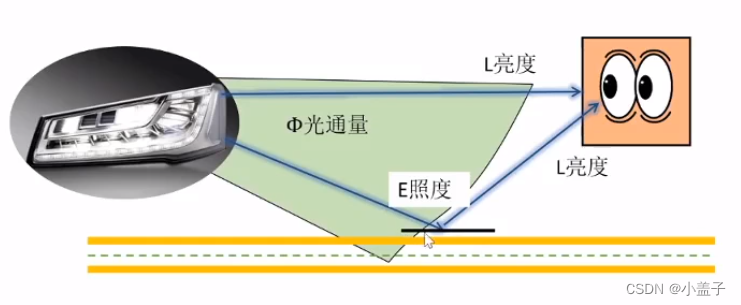
计算机图形辐照度学、光度学
文章目录 前言:一、什么是辐照度学二、什么是光度学 前言: 在计算机图形学中是把辐射(Radiance)等概念和亮度(Luminance)等概念不做区分的。辐射是辐照度学的概念,而亮度则是光度学上的概念。 辐照强高度并不意味着亮度就强,就比如…...
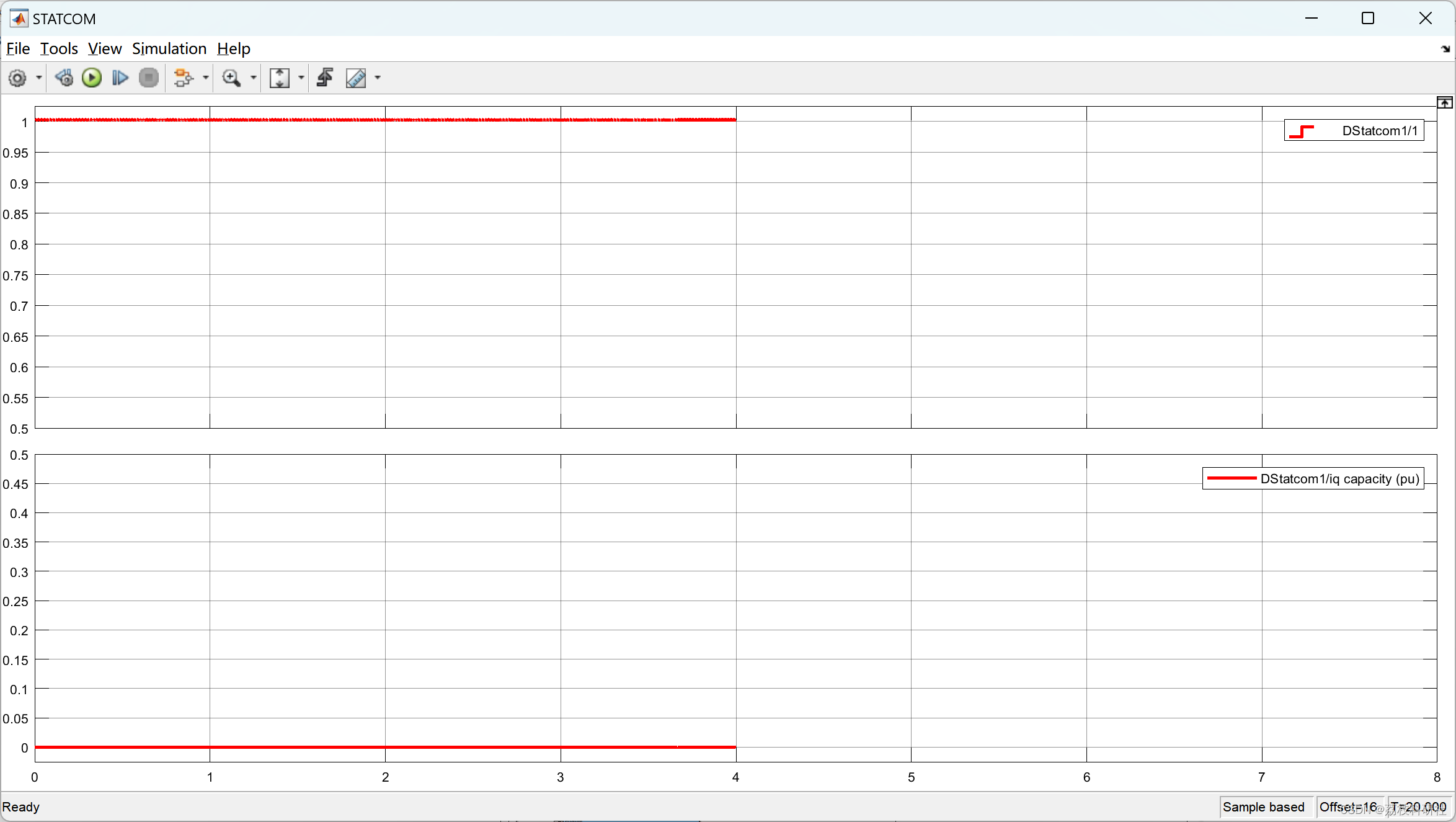
【无功功率控制】连接到无限电网的小型风电场的无功功率控制(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用pandas、xlrd、openpyxl读取Excel
首先创建一个示例Excel文件example.xlsx,其中包含以下数据: NameAgeGenderAlice28FemaleBob35MaleCharlie42MaleDave29MaleEve31Female 安装 pip install pandas pip install xlrd pip install openpyxl方法一:使用Pandas库 使用Pandas库来…...

Java面试题接口
Collection接口 List接口 迭代器 Iterator 是什么? Iterator 接口提供遍历任何 Collection 的接口。我们可以从一个 Collection 中使用迭代器方法来获取迭 代器实例。迭代器取代了 Java 集合框架中的 Enumeration,迭代器允许调用者在迭代过程中移…...
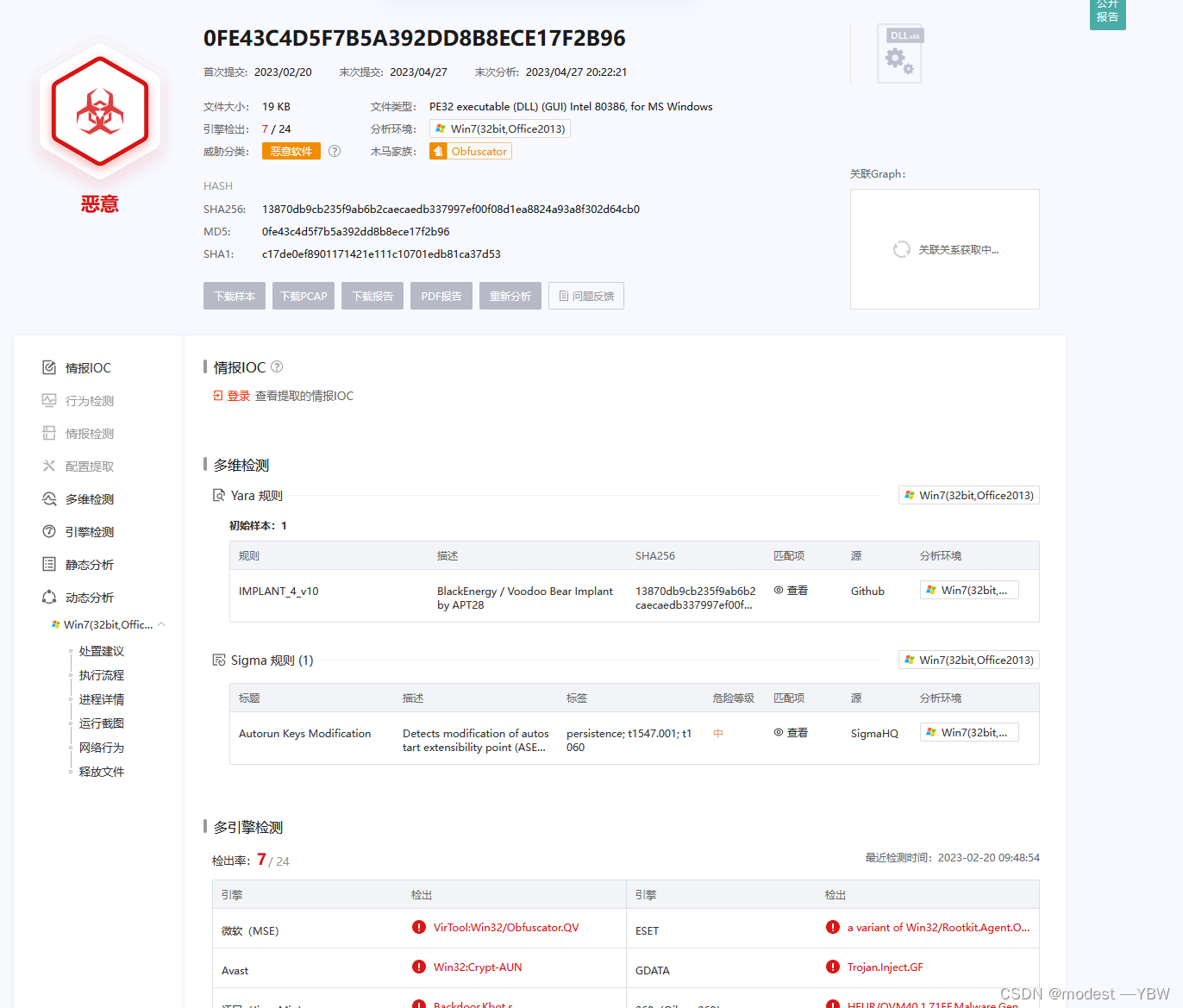
内存取证小练习-基础训练
这是题目和wolatility2.6的链接 链接:https://pan.baidu.com/s/1wNYJOjLoXMKqbGgpKOE2tg?pwdybww 提取码:ybww --来自百度网盘超级会员V4的分享 压缩包很小,题目也比较简单基础,可以供入门使用 1:Which volatility…...
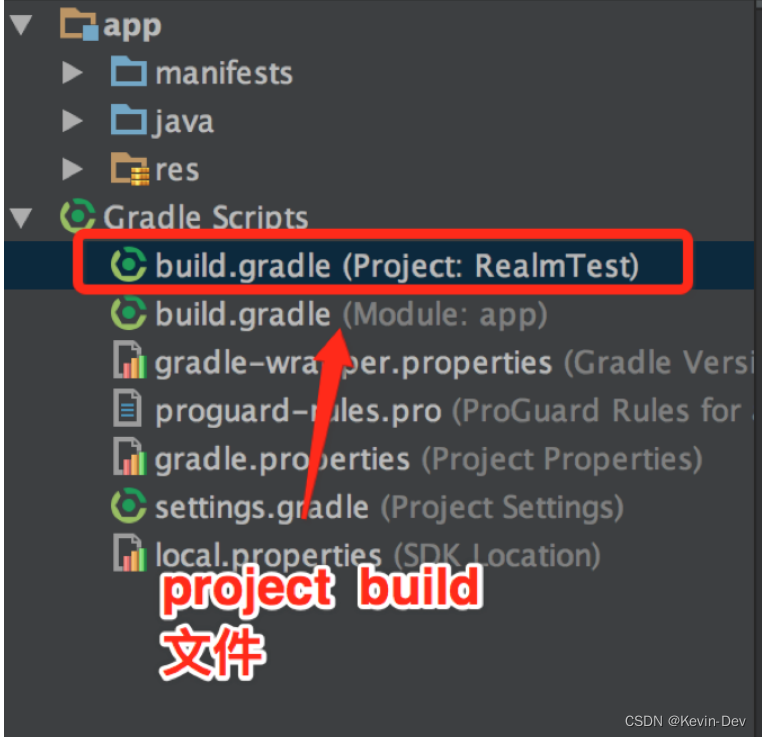
【Android -- 开源库】数据库 Realm 的基本使用
简介 Realm 是一个 MVCC (多版本并发控制)数据库,由Y Combinator公司在2014年7月发布一款支持运行在手机、平板和可穿戴设备上的嵌入式数据库,目标是取代 SQLite。Realm 本质上是一个嵌入式数据库,他并不是基于 SQLit…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
