低频量化之 可转债 配债数据及策略 - 全网独家
目录
历史文章
可转债配债数据
待发转债（进展统计）
待发转债（行业统计）
待发转债（5证监会通过，PE排序）
待发转债（5证监会通过，安全垫排序）
待发转债（5证监会通过，1手党）
待发转债（4发审委通过，PE排序）
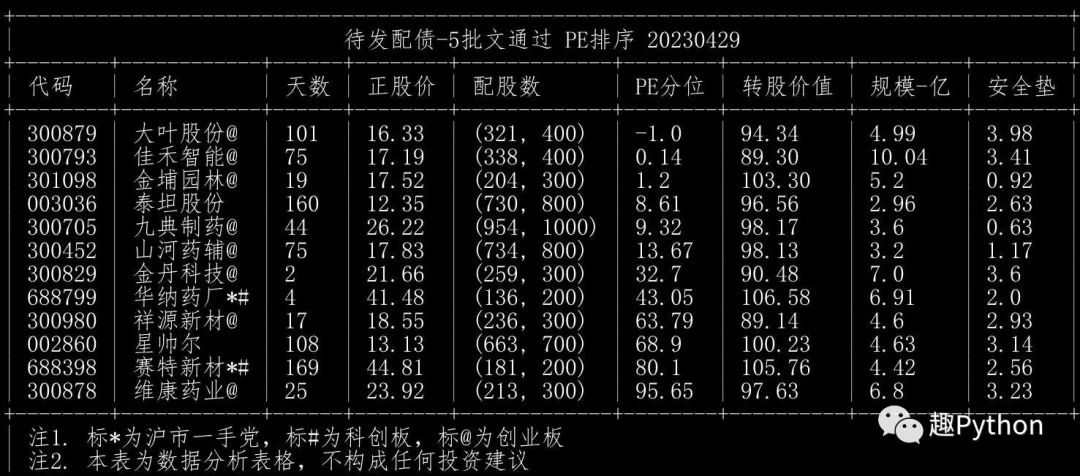
待发转债（4发审委通过，1手党）
待发转债（3证监会受理，按PE排序）
待发转债（3证监会/交易所受理，1手党）
待发转债（2股东大会通过，PE排序）
待发转债（2股东大会通过，1手党）
待发转债（1董事会通过，PE排序）
待发转债（1董事会通过，1手党）
待发转债（行业：银行）
待发转债（行业：半导体）
待发转债（行业：光学光电子）
待发转债（行业：专用设备）
待发转债（小规模<5亿）
可转债策略数据
低价格策略
低溢价策略
双低策略
四因子策略
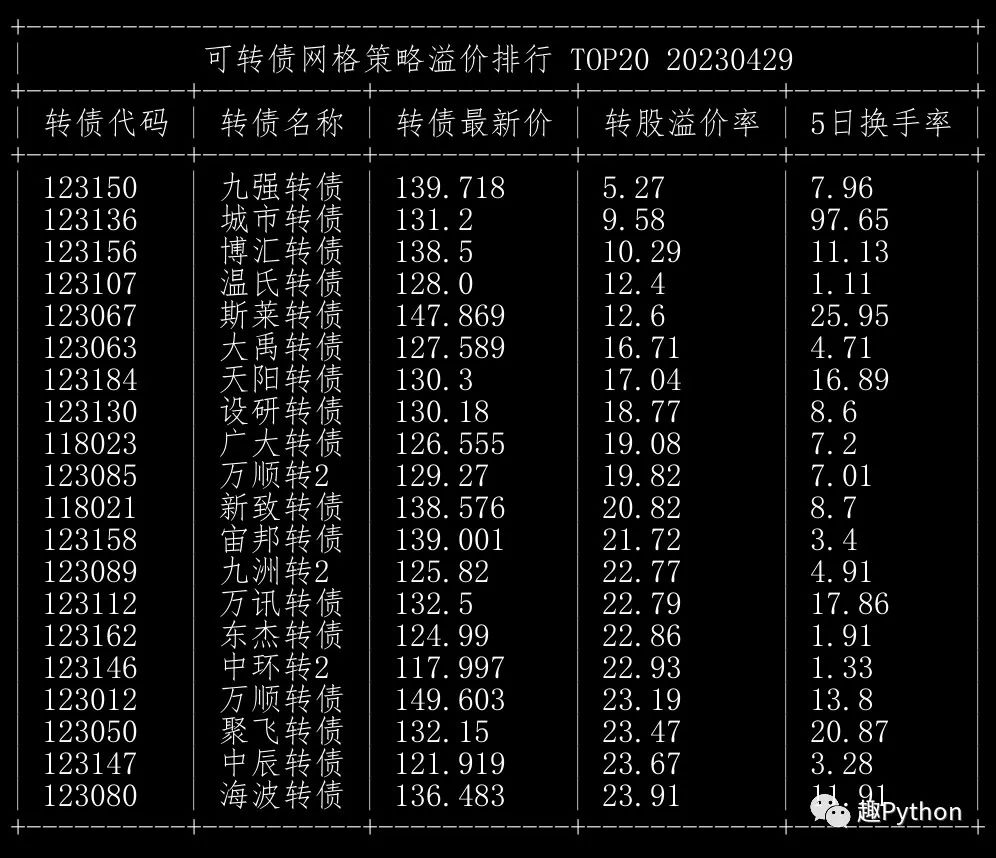
网格策略
最后
历史文章
股票系列
(策略)股票明日涨停预测
可转债系列
(打新)小白也可以科学的在股市里捡钱
(策略)小白也能懂的可转债上市价格预测
(策略)小白也能懂的可转债及可转债配债
(策略)小白也能懂的可转债配债价格计算
(策略)小白也能懂的可转债策略合集
可转债配债数据
待发转债（进展统计）
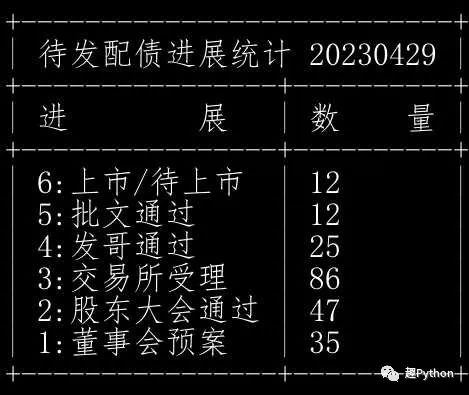
待发转债（行业统计）
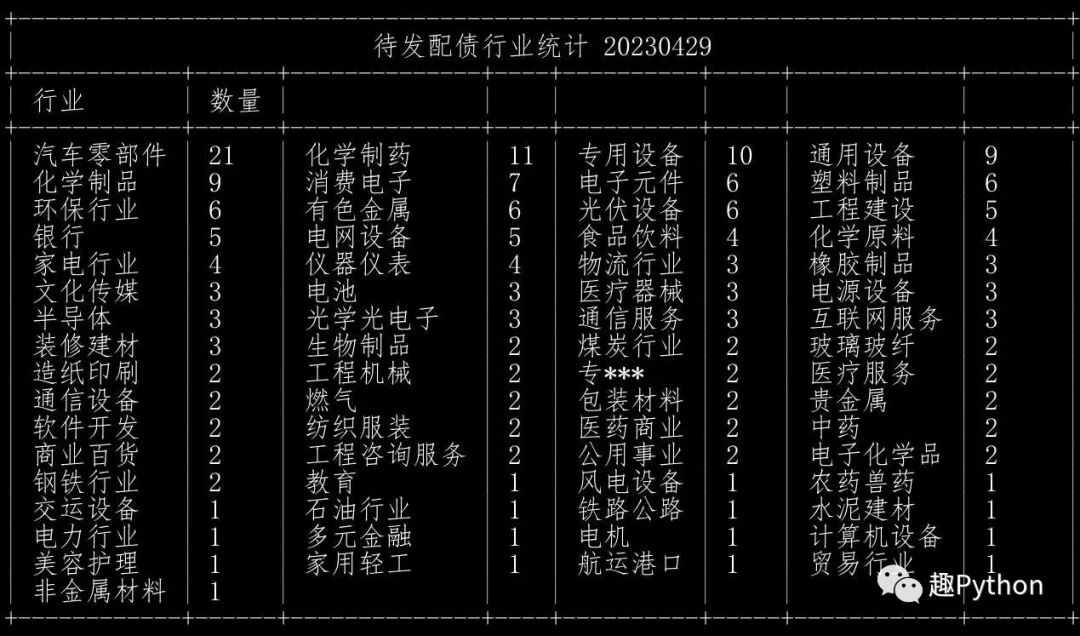
待发转债（5证监会通过，PE排序）
待发转债（5证监会通过，安全垫排序）
待发转债（5证监会通过，1手党）
待发转债（4发审委通过，PE排序）
待发转债（4发审委通过，1手党）
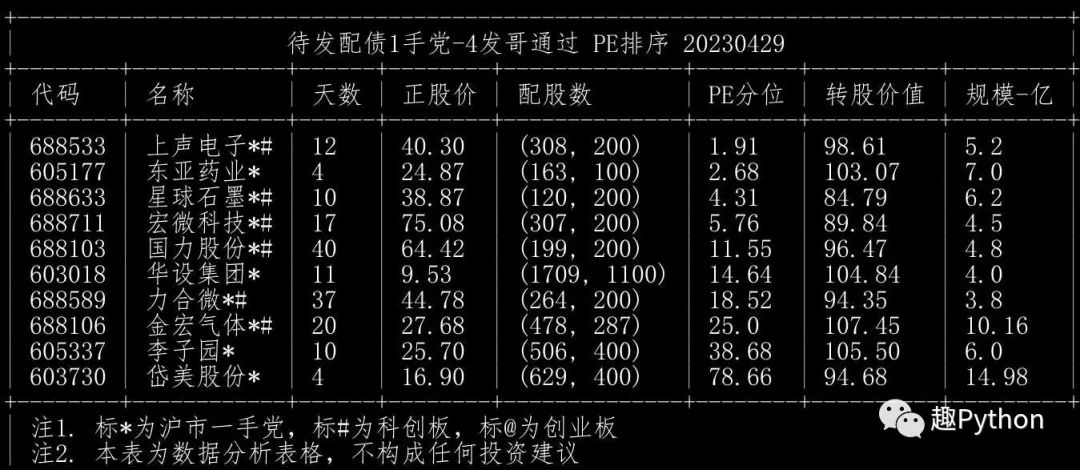
待发转债（3证监会受理，按PE排序）
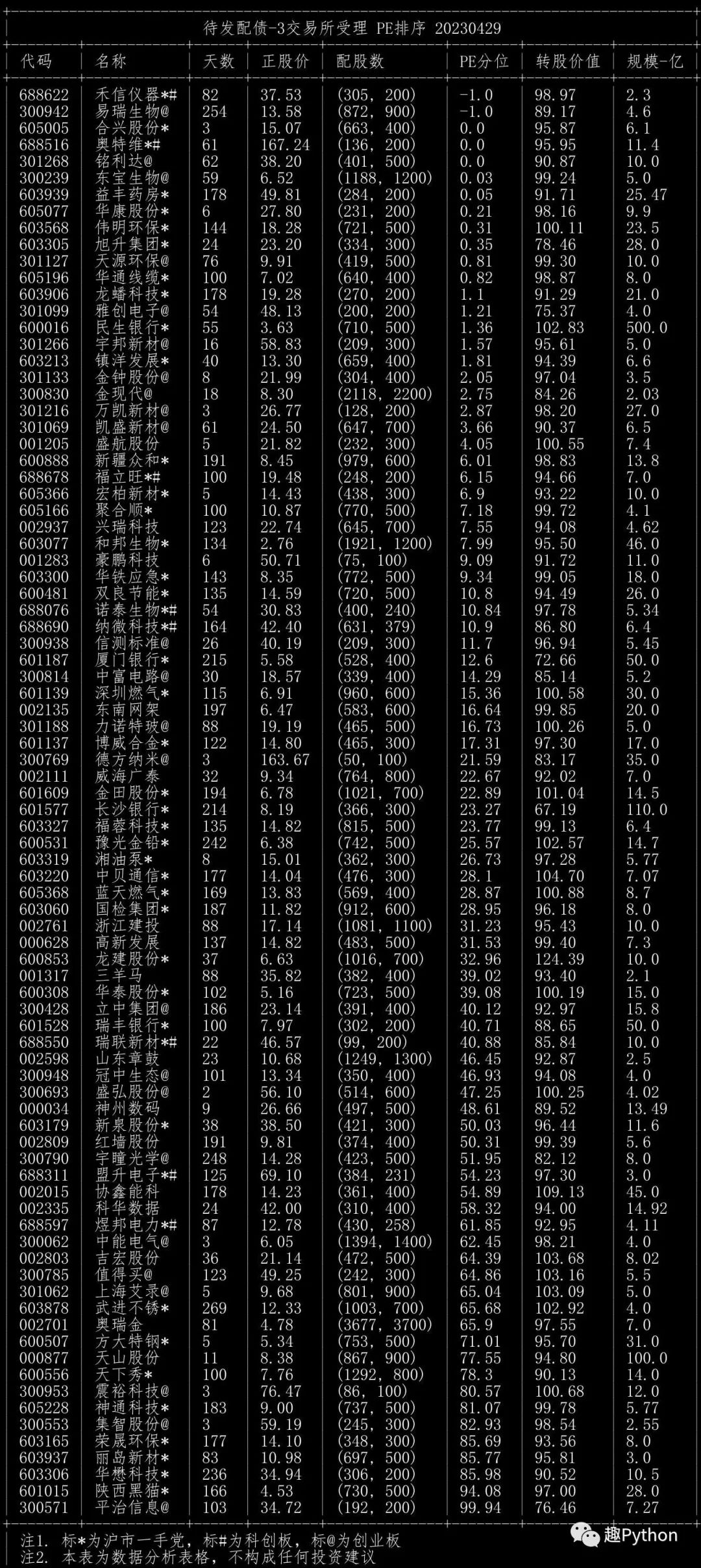
待发转债（3证监会/交易所受理，1手党）
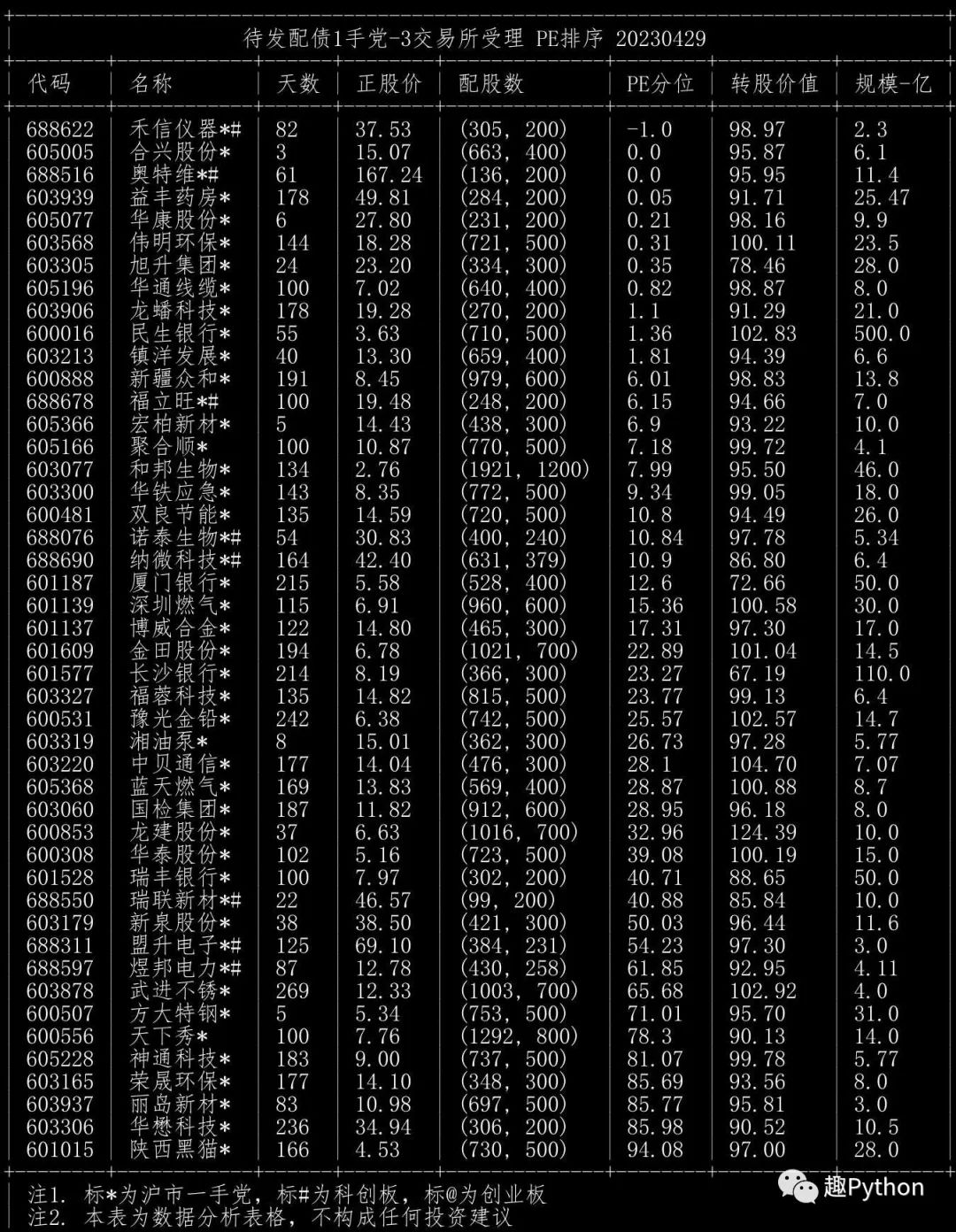
待发转债（2股东大会通过，PE排序）
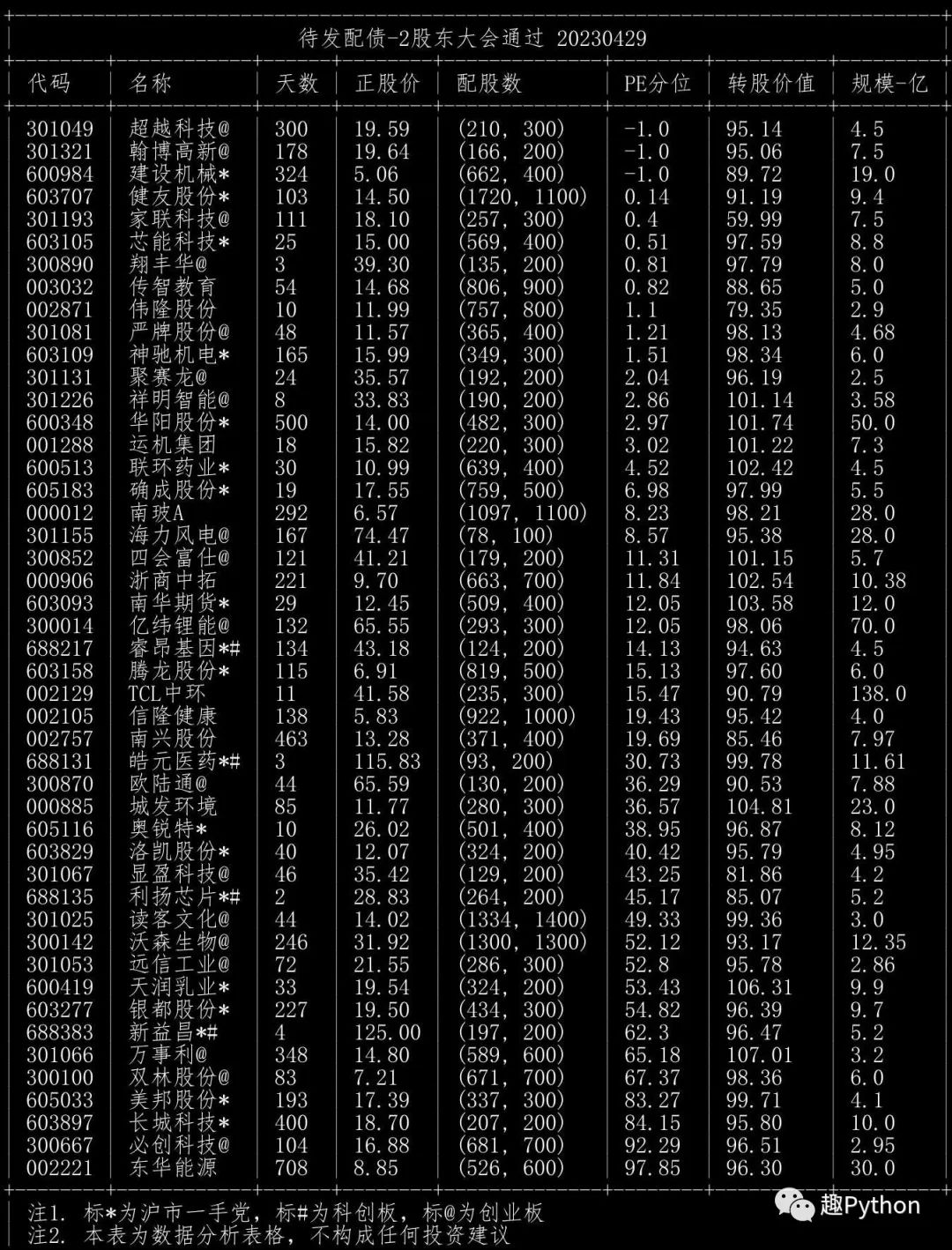
待发转债（2股东大会通过，1手党）
待发转债（1董事会通过，PE排序）
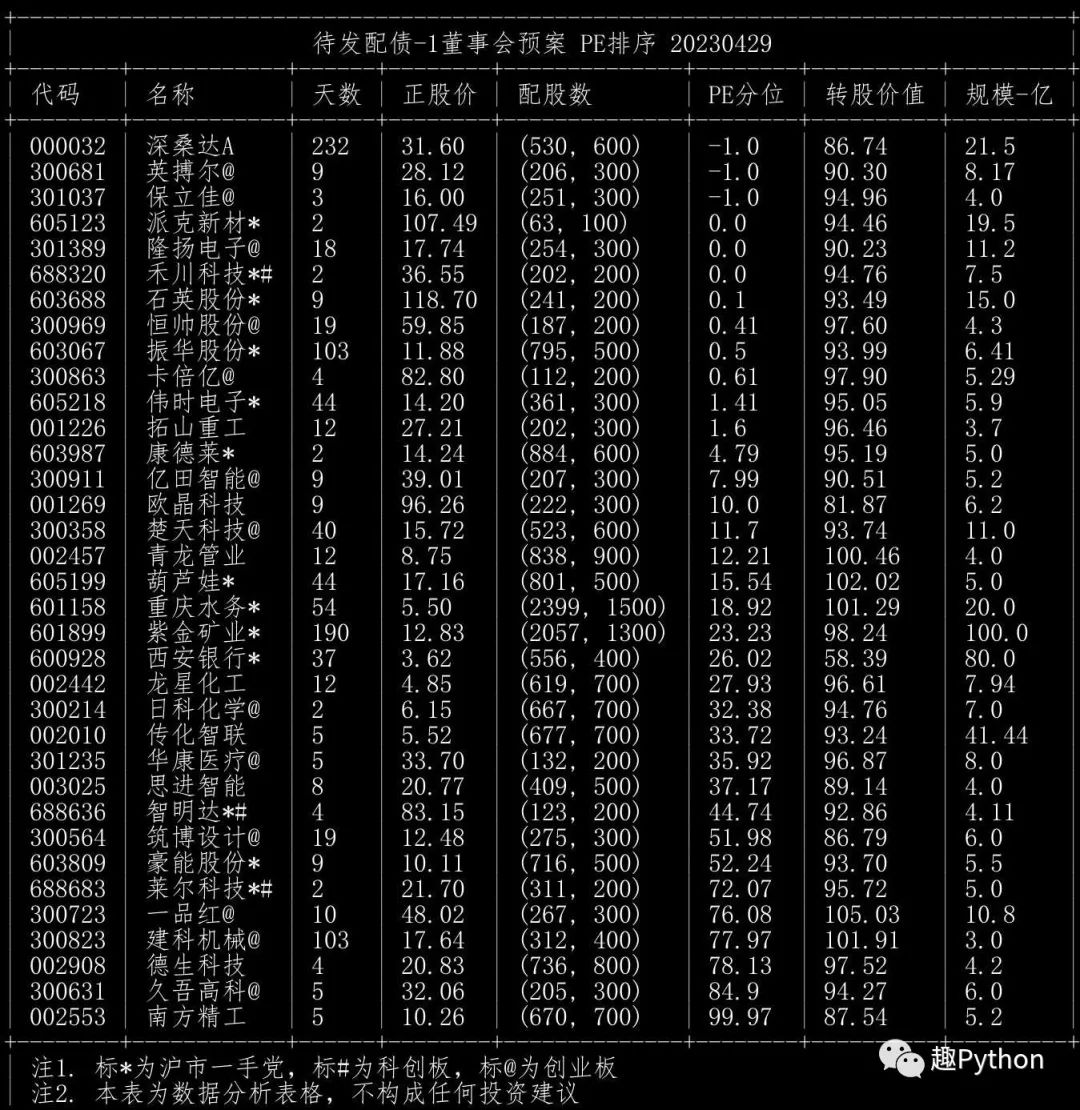
待发转债（1董事会通过，1手党）
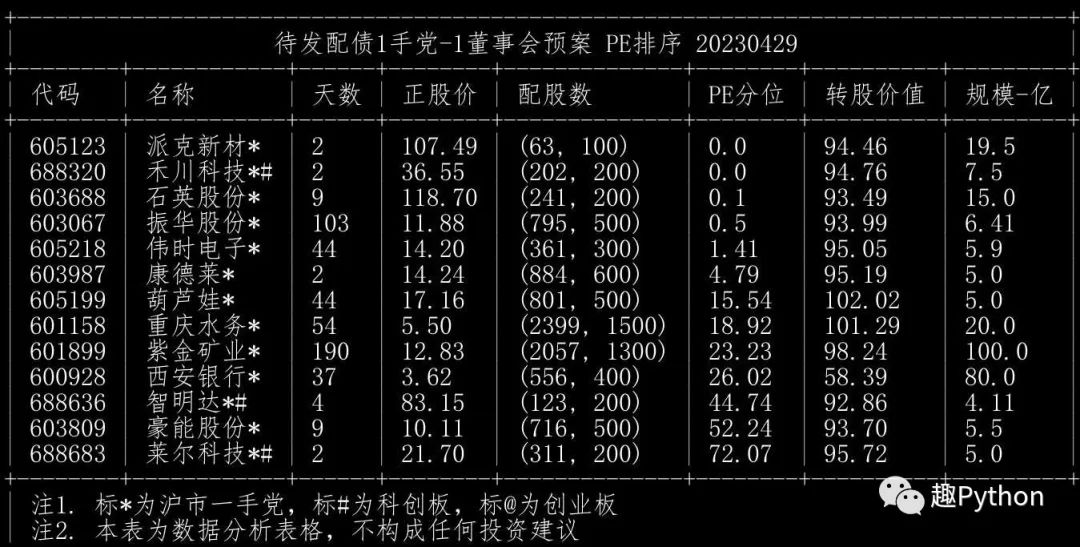
待发转债（行业：银行）
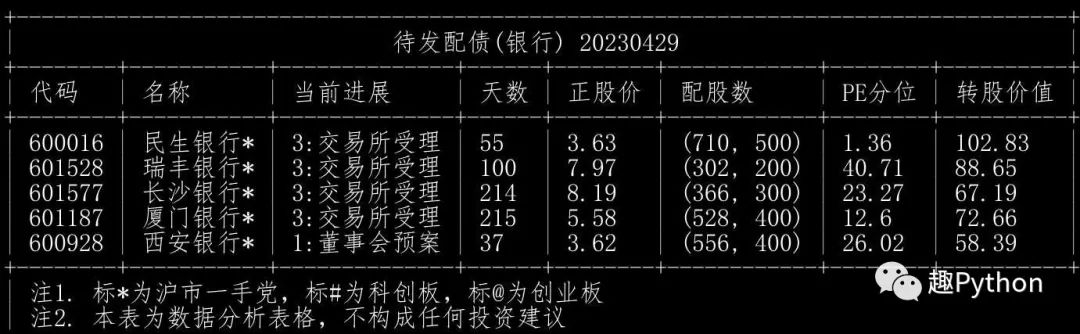
待发转债（行业：半导体）
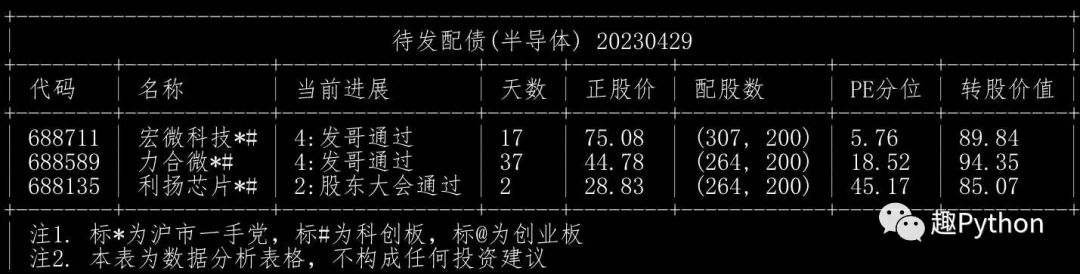
待发转债（行业：光学光电子）
待发转债（行业：专用设备）
待发转债（小规模<5亿）
可转债策略数据
低价格策略
低溢价策略
双低策略
双低值 = 可转债价格 + 转股溢价率 * 100
四因子策略
策略依据：
可转债价格 + 转股溢价率 * 50
换手率（>2%）
剩余规模（<5亿）
去除公告强赎的可转债
网格策略
策略依据：
价格低（< 150）
溢价低（< 41）
波动大（科创+创业）
换手率高
去除公告强赎的可转债
最后
本文，
包括本文所有数据图表均由作者Python程序而来，实属不易！~~
请帮忙点赞，分享和在看，谢谢！~
如有低频量化的交流，请留言，谢谢！~
相关文章：
低频量化之 可转债 配债数据及策略 - 全网独家
目录 历史文章可转债配债数据 待发转债（进展统计）待发转债（行业统计）待发转债（5证监会通过，PE排序）待发转债（5证监会通过，安全垫排序）待发转债（5证…...
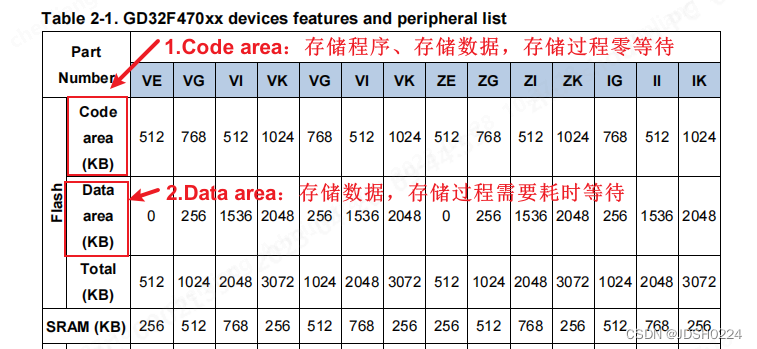
Code area 和Data area的区别
Code Area FLASH ：程序在这个flash运行时，几乎没有延时， 运行速度以时钟设置为准。 Data Area FLASH： 程序在这段flash运行时，每条语句都有延时， 最后的速度可能是以10M为时钟（举例）…...
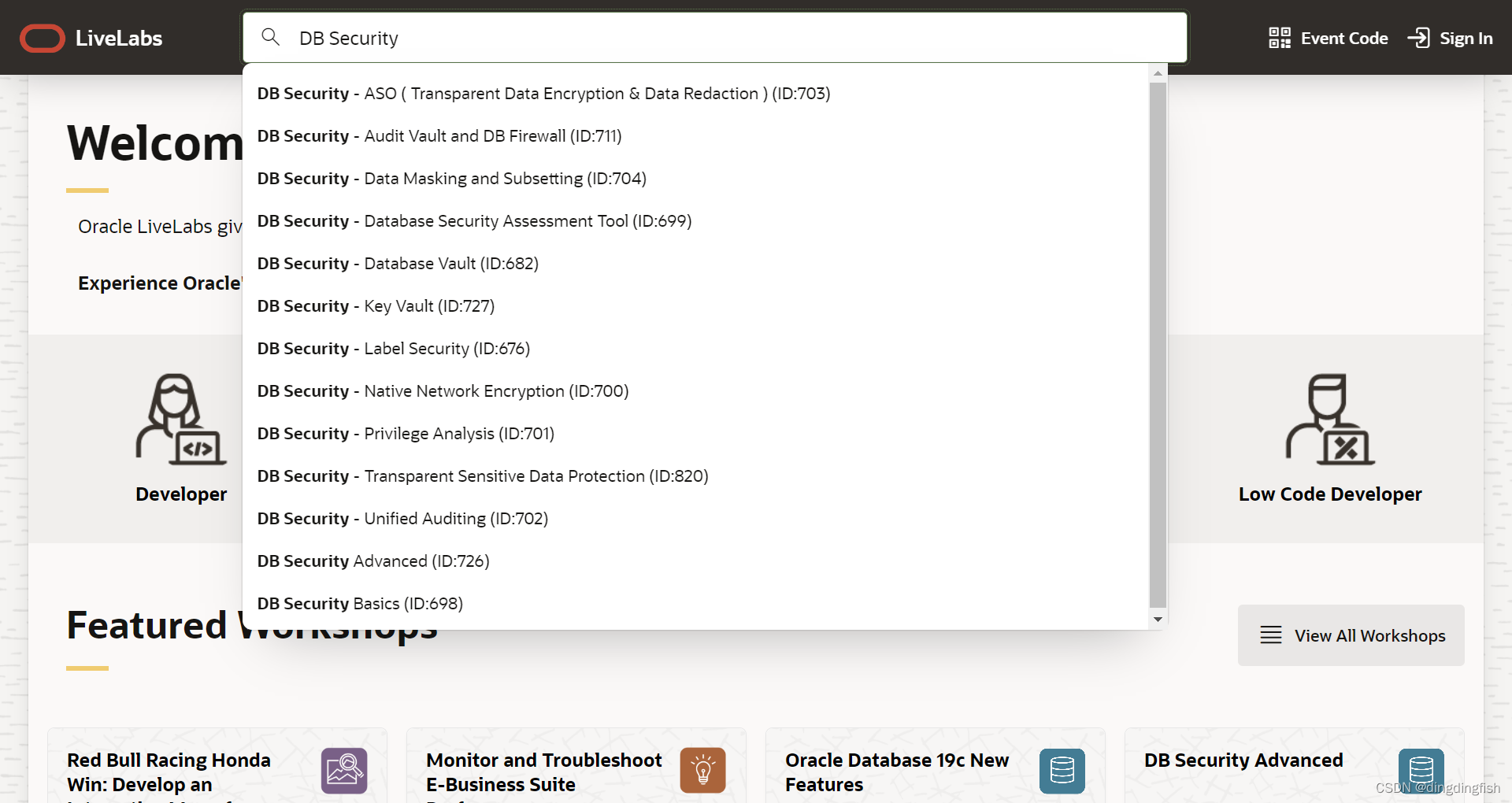
Oracle LiveLabs DB Security （数据库安全）实验汇总
在Oracle LiveLabs中，和数据库安全相关的实验分为2个系列，共12个实验。 Oracle数据库安全架构如下图： 这些实验涉及了Oracle安全相关的特性，企业版选件，独立产品和服务。 关于Oracle安全产品的中文主页可见&#…...
PAT A1012 The Best Rank
1012 The Best Rank 分数 25 作者 CHEN, Yue 单位 浙江大学 To evaluate the performance of our first year CS majored students, we consider their grades of three courses only: C - C Programming Language, M - Mathematics (Calculus or Linear Algrbra), and E -…...
“我和AI抠图网站的秘密情缘“
在浏览器里面意外发现了一个AI抠图工，了解了一下，AI抠图基于深度学习框架，结合智能检测识别技术，目前已能够实现高精视，秒级全自动主体、场景像素级识别等的分割能力。 一款好的抠图工具，可以把照片变得更加…...
最多能打多少场比赛呢
凌乱的yyy / 线段覆盖 题目背景 快 noip 了，yyy 很紧张！ 题目描述 现在各大 oj 上有 n n n 个比赛，每个比赛的开始、结束的时间点是知道的。 yyy 认为，参加越多的比赛，noip 就能考的越好（假的&#x…...
鸿蒙Hi3861学习二-程序烧录与日志输出
一、准备事项 开发板：BearPi-Hm Nano windows工具：HiBurn.exe https://pan.baidu.com/s/18OQD1_BvjNKD_J2e2iX3qg?pwdadrs 提取码：adrs windows工具：MobaXterm和RaiDrive 把ubuntu文件夹映射到windows本地。可以参考如下链接&am…...
typescript Awaited＜Type＞教程用法
typescript Awaited教程用法 文章目录 typescript Awaited<Type>教程用法 ts4.5发布了Awaited，但是很多人不明白Awaited的用法。 首先看一下官方的说明：这种类型旨在模拟函数await中的操作async，或 s.then()上的方法——特别是它们递归…...
AES硬件运算单元
功能描述 AES单元主要功能如下: 支持解密密钥扩展 支持128bit/192bit/256bit的密钥长度支持ECBCBCCTRM支持DMA进行自动数据传输 支持GF(2^128)域下的乘法，支持GMAC 工作模式 AES有4种工作模式，通过配置MODE1:0]寄存器设置。 模式1:用存储在AES KEYRx寄存…...
)
mulesoft MCIA 破釜沉舟备考 2023.04.28.26 (易错题)
mulesoft MCIA 破釜沉舟备考 2023.04.28.26 （易错题） 1. According to MuleSoft, what is a major distinguishing characteristic of an application network in relation to the integration of systems, data, and devices?2. An integration team follows MuleSoft’s r…...
k210单片机定时器的应用
定时器应该是一个单片机的标准配置，所以k210也是有的，拥有3个定时器，具体的使用方法我们往下看： 分步介绍： 首先是相关模块的使用 构造函数： machine.Timer(id,channel,modeTimer.MODE_ONE_SHOT,period100…...
linux0.12-7-1
[272页] 第7章 初始化程序 1、main.c主要内核初始化工作。 2、如果能完全理解这里调用的所有程序，那么看完这张内容后应该对Linux内核有了大致的了解。 3、 有一定的C语言知识 4、 需要GNU gcc手册在身边作为参考，因为在内核代码很多地方使用gcc的扩展…...
设置 文本框 自动填充背景颜色 为白色
关于autofill伪类的 兼容性： 在现代浏览器中，包括Chrome、Safari、Firefox等，都支持:autofill伪类，但在使用时必须加上浏览器前缀-webkit-，即:-webkit-autofill。 在旧版的浏览器中，可能不支持:autofill伪…...
Bitmap引起的OOM问题
作者：向阳逐梦 1.什么是OOM？为什么会引起OOM？ 答：Out Of Memory(内存溢出)，我们都知道Android系统会为每个APP分配一个独立的工作空间，或者说分配一个单独的Dalvik虚拟机，这样每个APP都可以独立…...
【JavaEE初阶】认识线程（Thread）
目录 🌾 前言 🌾 了解线程 🌈1.1 线程是什么？ 🌈1.2 一些基本问题 🌾2、创建线程的方式 🌈 2.1 继承Thread类 🌈 2.2 实现Runnable接口并重写run()方法 🌈 注意…...
自动化运维工具一Ansible Roles实战
目录 一、Ansible Roles概述 1.1.roles官方的目录结构 1.2.Ansible Roles依赖关系 二、Ansible Roles案例实战 2.1.Ansible Roles NFS服务 2.2 Roles Memcached 2.3 Roles-rsync服务 一、Ansible Roles概述 之前介绍了 Playbook 的使用方法，对于批量任务的部…...
json 中有递归parentId节点转 c#实体类时如何处理
如果您有一个具有递归parentId节点的JSON数据，并且您需要将其转换为C#实体类，则可以使用以下方法： 创建一个类来表示JSON对象的节点，包括它的属性和子节点。 public class Node {public int Id { get; set; }public string Name …...
给大家介绍几个手机冷门但好用的小技巧
技巧一：拍照识别植物 手机的拍照识别植物功能是指在使用手机相机时，可以通过对植物进行拍照，并通过植物识别技术，获取植物的相关信息和资料。其主要优点如下： 方便实用：使用拍照识别植物功能，…...
2.3 定点乘法运算
学习目标： 如果我要学习定点乘法运算，我会按照以下步骤进行学习： 确定学习目标：明确学习定点乘法运算的目的和重点，以便有针对性地进行学习。 掌握基础知识：首先需要了解定点数和定点乘法的基础知识&…...
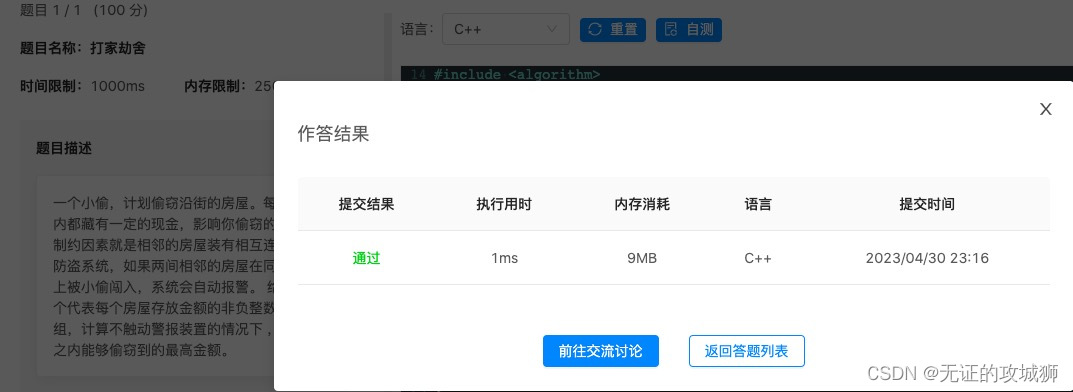
C++每日一练：打家劫室（详解动态规划法）
文章目录 前言一、题目二、分析三、代码总结 前言 这题目出得很有意思哈，打劫也是很有技术含量滴！不会点算法打劫这么粗暴的工作都干不好。 提示：以下是本篇文章正文内容，下面案例可供参考 一、题目 题目名称： 打家…...
8k长序列建模，蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂（如抗体、抑制肽）在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上，高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术，但这类方法普遍面临资源消耗巨大、研发周期冗长…...
华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
unix/linux，sudo，其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化，本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来，让我们拨开时间的迷雾，一同探寻 sudo 那波澜壮阔（也颇为实用主义）的发展历程。 历史背景：su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前，Unix 系统管理员和需要特权操作的…...
Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
根据万维钢·精英日课6的内容，使用AI（2025）可以参考以下方法：
根据万维钢精英日课6的内容，使用AI（2025）可以参考以下方法： 四个洞见 模型已经比人聪明：以ChatGPT o3为代表的AI非常强大，能运用高级理论解释道理、引用最新学术论文，生成对顶尖科学家都有用的…...
【HarmonyOS 5 开发速记】如何获取用户信息（头像/昵称/手机号）
1.获取 authorizationCode： 2.利用 authorizationCode 获取 accessToken：文档中心 3.获取手机：文档中心 4.获取昵称头像：文档中心 首先创建 request 若要获取手机号，scope必填 phone，permissions 必填 …...
管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
AI病理诊断七剑下天山，医疗未来触手可及
一、病理诊断困局：刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断"，医生需通过显微镜观察组织切片，在细胞迷宫中捕捉癌变信号。某省病理质控报告显示，基层医院误诊率达12%-15%，专家会诊…...
Mysql8 忘记密码重置，以及问题解决
1.使用免密登录 找到配置MySQL文件，我的文件路径是/etc/mysql/my.cnf，有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持：CMake支持多种操作系统和编译器，使用同一份构建配置可以在不同的环境中使用 简化配置：通过CMakeLists.txt文件，用户可以定义项目结构、依赖项、编译选项等，无需手动编写复杂的构建脚本…...