C++每日一练:打家劫室(详解动态规划法)
文章目录
- 前言
- 一、题目
- 二、分析
- 三、代码
- 总结
前言
这题目出得很有意思哈,打劫也是很有技术含量滴!不会点算法打劫这么粗暴的工作都干不好。
提示:以下是本篇文章正文内容,下面案例可供参考
一、题目
题目名称:
打家劫舍
题目描述:
一个小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组,计算不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
输入描述:
输入一个正整数n代表房屋的数量(n≤100),接着输入n个非负整数代表每间房屋的现金数量
输出描述:
小偷能偷取的最大金额。
示例1
输入
4
1 2 3 1
输出
4
二、分析
我们假设只有三个房间,事情就很简单了。做为专业小偷,我们知道,房屋编号是从0开始的,只能偷1号房屋或0号+2号房屋。为了取得最大战果,我们分别去看了看每个房屋能偷到多少。出门比较一下,就知道结果了。
我们逛完了三个房屋,现在站在第2号房屋门口来思考一下,就是选择0和2,或选1的问题。
我们把0+2能偷到的钱先记在2号房屋门上,把1号能偷到的钱记在1号门上,然后去看看3号房屋有多少钱可偷。这样1、2、3号房屋又成了一个同样的选择…
我们不停的在门上记录能偷到的钱,不停的用同样的方法选择。
拿示例来说,我们在1号房屋门上记上2毛,2号房屋门上记上4毛(0号加2号),然后和3号房屋来比较,显然4毛大于1号的2毛加3号的1毛。侦察完成,就偷0号加2号了!
再找个长点的例子:
1 2 3 2 9 1 2
同样先在1号房屋门上记上2毛,2号房屋门上记4毛(0号+2号),侦察完3号房屋后,就成了:
2 4 2 9 1 2
继续侦察下一家:
4 4 9 1 2
4 (13) 1 2
(13) 5 2
5 (15)
(15)
最后偷得15毛!
三、代码
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <algorithm>using namespace std;int solution(int n, std::vector<int>& vec){int result=0;// TODO:vector<int> tmp={vec[0], max(vec[0], vec[1])};if(n==1) return tmp[0];if(n==2) return tmp[1];for (int i=2; i<n; ++i){tmp[i] = max(tmp[i-1], tmp[i-2]+vec[i]);}result = tmp[n-1];return result;
}int main() {int n;std::vector<int> vec;std::cin>>n;std::string line_0, token_0;getline(std::cin >> std::ws,line_0);std::stringstream tokens_0(line_0);while(std::getline(tokens_0, token_0, ' ')){vec.push_back(std::stoi(token_0));}int result = solution(n,vec);std::cout<<result<<std::endl;return 0;
max(vec[0], vec[1])这一句解决了前二个房屋的选择,因为第二个房屋我们必须选前两个中最大的。如果0号是最大的,就把1号变成0号一样,再来继续选择。
举例来看:
7 1 1 2
侦察前二个房屋后就是:
7 7 1 2
然后7 8 2
最后9
如果是这样的:
1 7 2 1
侦察前二个后就还是:
1 7 2 1
所以初始化的时候一定要考虑清楚!
总结
所谓动态规划:就是将问题划分为一系列子问题,求各子问题的最优解,然后以自底向上的方式递归地从子问题的最优解构造出整个问题的最优解。
在本例中,我们把n个房屋不停的当作三个房屋来处理。所以我们设计了一个tmp数组来存储过程数据。
动态规划和分治法有点像,都是把复杂问题分解成简单的小问题。
不过动态规划的子问题之间不是独立的,子问题的解往往会在下一个选择中被使用。
而分治法,一般会把一个复杂的问题分解成若干个独立的子问题,求解子问题后再合成本问题的解。今天的 “小艺照镜子” (本专栏的另一篇文章有详解)就是用分治法解的。
相关文章:

C++每日一练:打家劫室(详解动态规划法)
文章目录 前言一、题目二、分析三、代码总结 前言 这题目出得很有意思哈,打劫也是很有技术含量滴!不会点算法打劫这么粗暴的工作都干不好。 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目 题目名称: 打家…...

Wireshark使用
Capture Filters 语法 <Protocol name><Direction><Hosts><Value><Logical operations><Expressions> e.g 1.tcp src port 443 只抓取来源端口是443的tcp数据 2.not arp 不获取arp数据 3.port 80 获取端口是80的数据,不指…...

这才是 SpringBoot 统一登录鉴权、异常处理、数据格式 的正确姿势
本篇将要学习 Spring Boot 统一功能处理模块,这也是 AOP 的实战环节 用户登录权限的校验实现接口 HandlerInterceptor WebMvcConfigurer 异常处理使用注解 RestControllerAdvice ExceptionHandler 数据格式返回使用注解 ControllerAdvice 并且实现接口 Response…...
Java面试题总结 | Java面试题总结6-MYSQL模块(持续更新)
Mysql 文章目录 Mysql关系型数据库和非关系型数据库的区别什么是ORM?-**mybatis**如何评估一个索引创建的是否合理?Count函数执行效果上:执行效率上:count(主键)和count(列名) 数据库的三大范式Mysql中char和varchar的区别数据库设计或者功能…...
)
Linux命令集(Linux文件管理命令--mv指令篇)
Linux命令集(Linux文件管理命令--mv指令篇) Linux文件管理命令集(mv指令篇)2. mv(move)1. 文件移动2. 递归移动目录3. 文件目录重命名4. 强制移动5. 备份覆盖的目标文件6. 试探性移动7. 显示移动进度8. 补集操作9. 修改文件的权限…...

不一样的 Git 之间 | GitLab vs GitHub vs Gitee vs GitCode
Git仓库对比:GitLab vs GitHub vs Gitee vs GitCode 在软件开发中,版本控制是必不可少的工具之一。Git作为目前最为流行的版本控制系统,也逐渐成为了开发者们的标配。但是,如何选择一个合适的Git仓库来存储您的代码呢?…...

海尔牵头IEEE P2786国际标准通过Sponsor投票并连任工作组主席
01 海尔牵头IEEE P2786国际标准 通过Sponsor投票 并连任工作组主席 海尔牵头制定的全球首个服装物联网国际标准IEEE P2786《Standard for General Requirements and Interoperability for Internet of Clothing》通过Sponsor投票,标志着该国际标准草案得到了行业…...
倾斜摄影超大场景的三维模型的顶层合并的纹理压缩与抽稀处理技术分析
倾斜摄影超大场景的三维模型的顶层合并的纹理压缩与抽稀处理技术分析 倾斜摄影超大场景的三维模型的顶层合并需要对纹理进行压缩和抽稀处理,以减小数据量和提高数据的传输和展示性能。以下是一种常用的纹理压缩和抽稀处理技术: 1、纹理图集 纹理瓦片化…...

linux命令之iostat详解
iostat 监视系统输入输出设备和CPU的使用情况 推荐Linux命令在线工具:linux在线查询工具 补充说明 iostat命令 被用于监视系统输入输出设备和CPU的使用情况。它的特点是汇报磁盘活动统计情况,同时也会汇报出CPU使用情况。同vmstat一样,ios…...

【C++】程序员必备知识:认识类与对象
【C】程序员必备知识:认识类与对象 ①.面向过程和面向对象②.类的引入③.类的定义Ⅰ.定义方式Ⅱ.命名规则建议: ④.类的访问限定符及封装Ⅰ.访问限定符Ⅱ.封装 ⑤.类的作用域⑥.类的实例化⑦.类的对象大小计算Ⅰ.如何计算?Ⅱ.类对象存储方式Ⅲ…...
python基础实战5-python基本结构
1 if语句 if语句是用来进行判断的,其使用格式如下 if 要判断的条件: 条件成立时,要做的事情 案例一: age 30 print("------if判断开始------") if age > 18:print("我成年了") print("------if判断…...
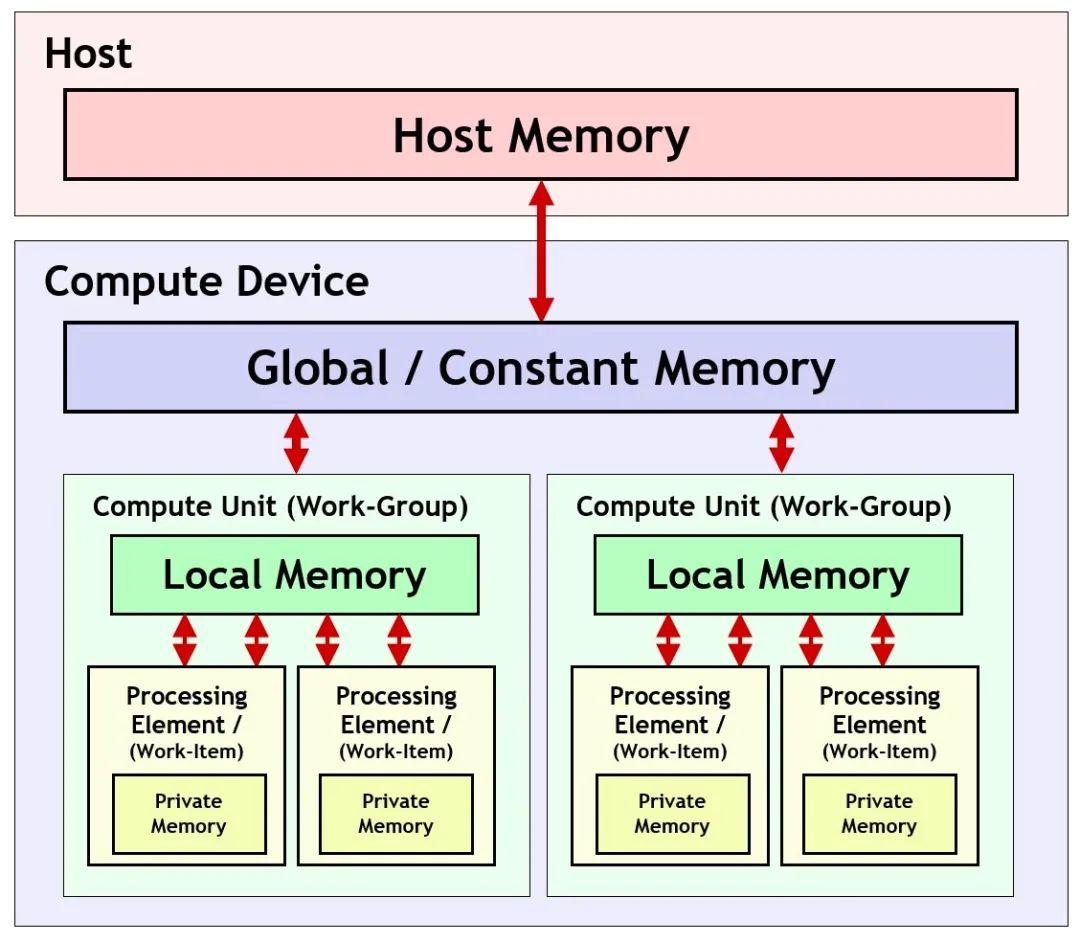
移动端异构运算技术 - GPU OpenCL 编程(基础篇)
一、前言 随着移动端芯片性能的不断提升,在移动端上实时进行计算机图形学、深度学习模型推理等计算密集型任务不再是一个奢望。在移动端设备上,GPU 凭借其优秀的浮点运算性能,以及良好的 API 兼容性,成为移动端异构计算中非常重要…...
)
QString类方法和变量简介(全)
QString类方法和变量简介 操作字符串(|append|insert|sprintf|QString::arg()|prepend|replace|trimmed|simplified)查询字符串(startsWith|endsWith|contains|localeAwareCompare|compare)字符串转换 标准C提供了两种字符串:一种是C语言风格的以"\0"字符…...
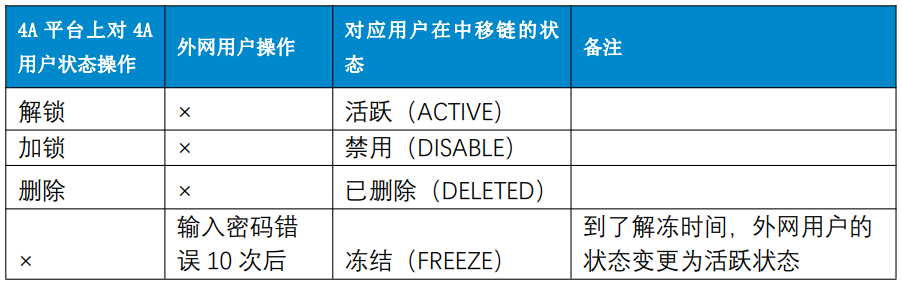
中移链控制台对接4A平台功能验证介绍
中移链控制台具备单独的注册登录页面,用户可通过页面注册或者用户管理功能模块进行添加用户,通过个人中心功能模块进行用户信息的修改和密码修改等操作,因业务要求,需要对中移链控制台的用户账号进行集中管理,统一由 4…...

必知的Facebook广告兴趣定位技巧,更准确地找到目标受众
在Facebook广告投放中,兴趣定位是非常重要的一环。兴趣定位不仅可以帮助我们找到我们想要的目标受众,还可以帮助我们避免一些常见的坑。今天,就让我们一起来看看必知的Facebook广告兴趣定位技巧,更准确地找到目标受众。 1.不要只关…...
)
【MySQL】慢查询+SQL语句优化 (内容源自ChatGPT)
慢查询SQL语句优化 1.什么是慢查询2.优化慢查询3.插入数据优化5.插入数据底层是什么6.页分裂7.页合并8.主键优化方式10.count 优化11.order by优化12.group by 优化13.limit优化14.update 优化15.innodb 三大特征 1.什么是慢查询 慢查询是指执行SQL查询语句所需要的时间较长&a…...

HashMap底层源码解析及红黑树分析
HashMap线程不安全,底层数组链表红黑树 面试重点是put方法,扩容 总结 put方法 HashMap的put方法,首先通过key去生成一个hash值,第一次进来是null,此时初始化大小为16,i (n - 1) & hash计算下标值&a…...

科技云报道:一路狂飙的ChatGPT,是时候被监管了
科技云报道原创。 即使你过去从不关注科技领域,但近期也会被一个由OpenAI(美国的一家人工智能公司)开发的人工智能聊天机器人“ChatGPT”刷屏。 与上届“全球网红”元宇宙不同,这位新晋的“全能网友”似乎来势更加凶猛。 互联网…...

第四十四章 管理镜像 - 传入日记传输率
文章目录 第四十四章 管理镜像 - 传入日记传输率传入日记传输率镜像数据库状态 第四十四章 管理镜像 - 传入日记传输率 传入日记传输率 在备份和异步成员的镜像成员状态列表下方,自上次刷新镜像监视器以来日志数据从主服务器到达的速率显示在该成员的传入日志传输…...
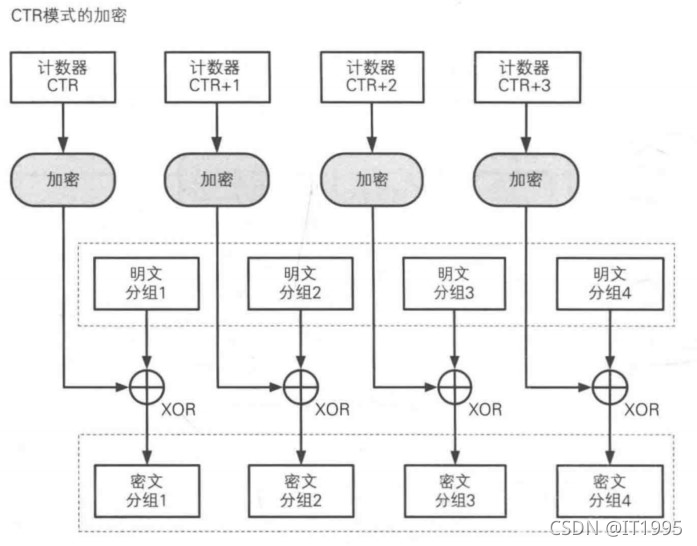
加密解密学习笔记
加密种类 对称加密,分组对称加密算法 加密算法 AES(Advanced Encryption Standard)高级加密标准 DES(Data Encryption Standard)数据加密标准 3DES/Triple DEA (Triple Data Encryption Algorithm) 三重数据加密算…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
