通达信顾比倒数线指标公式,信号不漂移
顾比倒数线是由技术派大师戴若·顾比发明的,该指标利用三个重要的价格来判断入场或离场时机,可用于盘后制定下一个交易日的操作计划。此外,顾比倒数线还可以用于补充验证其他指标。
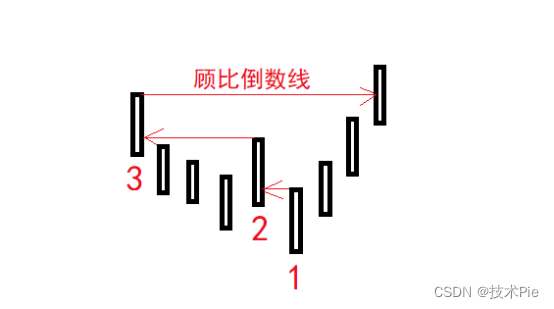
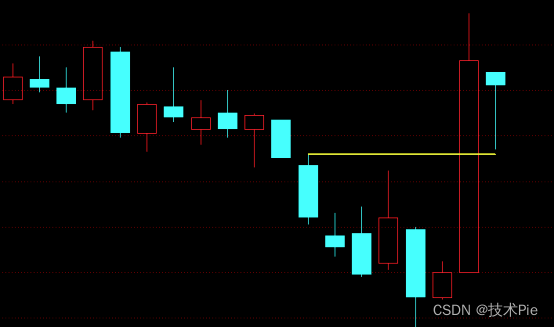
在编写顾比倒数线选股公式之前,需要先了解顾比倒数线的画法。以低点为例(如下图):
1、找到最低点对应的K线,这是第1根重要K线;
2、从第1根重要K线向左倒数,出现最高价高于第1根重要K线的最高价,这是第2根重要K线;
3、从第2根重要K线向左倒数,出现最高价高于第2根重要K线的最高价,这是第3根重要K线;
4、从第3根重要K线最高价画一条直线,这就是“顾比倒数线”。
一、CONST函数
编写公式需要使用CONST函数。
含义:CONST(X),取X的最后一天的值为常量
举例:LLV(L,10)表示10日最低价的最低值,CONST(LLV(L,10))就表示取10日最低价的最低值的最后一天的值为常量。太拗口了,直接看例子吧。
A1:LLV(L,10);
A2:CONST(LLV(L,10));
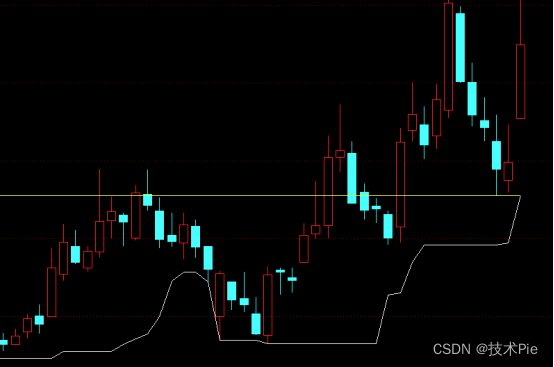
A1:LLV(L,10);如下图白线所示,结果会随着行情的发展而不断变化,显示的是动态的结果。
A2:CONST(LLV(L,10));如下图黄水平线,CONST(LLV(L,10))跟着LLV(L,10)的最新值变化,比如LLV(L,10)今天的值是15,CONST(LLV(L,10))就是以15画一条水平线;明天LLV(L,10)的值变成16,CONST(LLV(L,10))就以16画一条水平线。A2:CONST(LLV(L,10));显示的是静态的结果。
举个不太恰当的例子,A1:LLV(L,10);相当于你在看视频,A2:CONST(LLV(L,10));就相当于把视频暂停了,你看到的暂停画面。
二、顾比倒数线主图指标公式
思路:
1、计算第1根重要K线的最高价。首先,定位最低点。用眼睛看图,很容易看出波段低点,但是量化没这么简单。本例取10日最低点,这个参数可以自行修改。用BARSLAST计算第1根重要K线(10日最低点)距离现在的周期数,然后用REF函数返回到第1根重要K线,取其最高价,得到第1根重要K线的最高价。用CONST把这个最高价定格住,不然没法和之前的最高价比较。
T1:=BARSLAST(L=LLV(L,10));
H1:CONST(REF(H,T1));
2、计算第2根重要K线的最高价。用REF函数返回到第1根重要K线,再用BARSLAST函数计算第2根重要K线(最高价高于第1根重要K线的最高价)距离第1根重要K线的周期数,再把周期数加起来,得到第2根重要K线距离现在的周期数。用REF函数返回到第2根重要K线,取其最高价,得到第2根重要K线的最高价,用CONST定格住这个最高价。
T2:=REF(BARSLAST(H>H1),T1+1)+T1+1;
H2:CONST(REF(H,T2));
3、计算第3根重要K线的最高价,和第2根过程类似,就不详细解释了。
T3:=REF(BARSLAST(H>H2),T2+1)+T2+1;
H3:CONST(REF(H,T3));
经过以上计算,三根重要K线对应的高点画出三条水平线,如下图。
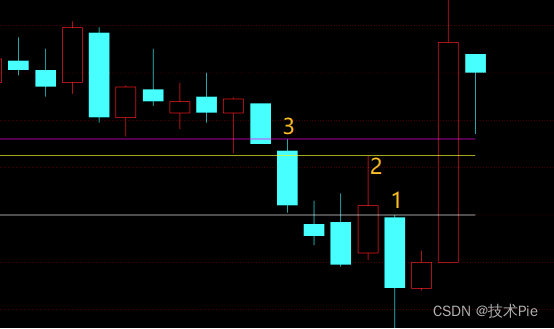
第3根重要K线对应的最高价画线就是顾比倒数线,用DRAWSL函数可以画出来。
顾比倒数线主图公式:
T1:=BARSLAST(L=LLV(L,10));
H1:=CONST(REF(H,T1));
T2:=REF(BARSLAST(H>H1),T1+1)+T1+1;
H2:=CONST(REF(H,T2));
T3:=REF(BARSLAST(H>H2),T2+1)+T2+1;
H3:=CONST(REF(H,T3));
DRAWSL(ISLASTBAR,H3,0,T3,1),LINETHICK2,COLORYELLOW;{从最后一个周期往左到第3根重要K线画线};
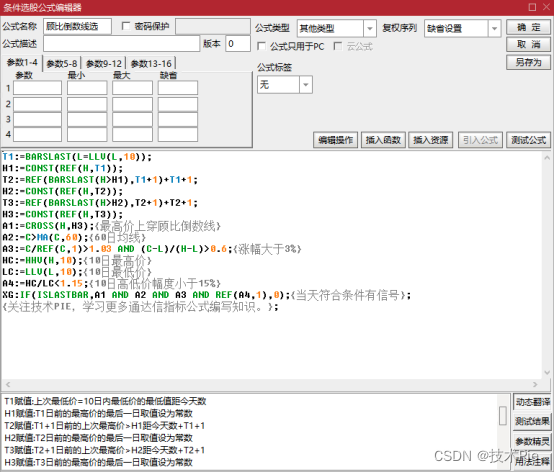
三、顾比倒数线选股公式
T1:=BARSLAST(L=LLV(L,10));
H1:=CONST(REF(H,T1));
T2:=REF(BARSLAST(H>H1),T1+1)+T1+1;
H2:=CONST(REF(H,T2));
T3:=REF(BARSLAST(H>H2),T2+1)+T2+1;
H3:=CONST(REF(H,T3));
A1:=CROSS(H,H3);{最高价上穿顾比倒数线}
A2:=C>MA(C,60);{60日均线}
A3:=C/REF(C,1)>1.03 AND (C-L)/(H-L)>0.6;{涨幅大于3%}
HC:=HHV(H,10);{10日最高价}
LC:=LLV(L,10);{10日最低价}
A4:=HC/LC<1.15;{10日高低价幅度小于15%}
XG:IF(ISLASTBAR,A1 AND A2 AND A3 AND REF(A4,1),0);{当天符合条件有信号};
四、注意点
1、顾比倒数线选股公式仅仅是举例,简单做了筛选。其实顾比倒数线应该像文章开头所说,结合其他指标使用,可以作为其他指标的触发信号,用来判断进场时机。
2、CONST函数通达信虽然没有标注为未来函数,但是有未来函数的性质,不当使用可能会导致信号漂移。漂移的原因从之前的举例就可以看出来,比如X今天的值是15,CONST(X)就是以15画一条水平线;明天X的值变成16,CONST(X)就以16画一条水平线。也就是说历史的CONST(X)值会变化的,这个过程会导致原来不满足条件的情况变成满足条件。本文的公式利用ISLASTBAR函数把历史信号屏蔽了,这样就不会有漂移的问题。不过因为用了CONST、ISLASTBAR,主图公式、选股公式只有最近一次产生信号。
3、如何判断信号会不会漂移呢?可以通过通达信的沙盘推演、训练模式这两个功能,通过行情的不断发展,查看行情变动过程中信号是否会漂移。本文的公式因为只显示最近一次,随着行情发展,之前的信号会消失,但这和信号漂移有本质区别,不要搞错了。
顾比倒数线公式代码不长,寥寥几行,其中蕴含的我的思考过程却是复杂而丰富的,编写不易啊!
关注技术Pie,学习更多通达信指标公式编写知识。
友情提醒:本文仅供学习交流技术指标公式,不构成任何投资建议。投资有风险,入市需谨慎!
相关文章:

通达信顾比倒数线指标公式,信号不漂移
顾比倒数线是由技术派大师戴若顾比发明的,该指标利用三个重要的价格来判断入场或离场时机,可用于盘后制定下一个交易日的操作计划。此外,顾比倒数线还可以用于补充验证其他指标。 在编写顾比倒数线选股公式之前,需要先了解顾比倒…...

网络安全: CIDR无类别路由
网络安全: CIDR无类别路由 CIDR是无类别路由,出现CIDR的原因是因为ipv4的地址被使用完客,CIDR的出现暂缓了ipv4用完的速度。 原本的ipv4很刻板,网络号分成8位,16位,24位作为掩码,也就是 xxx.0…...

NetMQ | 发布订阅时使用含通配符的Topic
NetMQ | 发布订阅时使用含通配符的Topic 文章目录 NetMQ | 发布订阅时使用含通配符的Topic前言通配符如何使用通配符通配符的作用结束语 前言 今天我来介绍一下NetMQ发布订阅时如何使用含通配符的Topic,让我们能够更加灵活地订阅消息。 什么是Topic? 在NetMQ中&am…...

行为型模式-模板方法模式
模板方法模式 概述 在面向对象程序设计过程中,程序员常常会遇到这种情况:设计一个系统时知道了算法所需的关键步骤,而且确定了这些步骤的执行顺序,但某些步骤的具体实现还未知,或者说某些步骤的实现与具体的环境相关…...
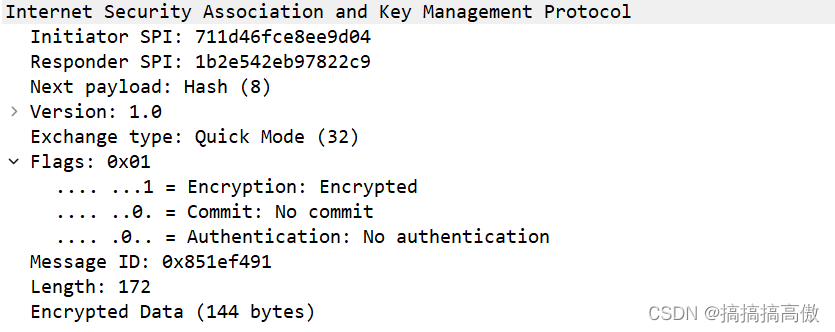
IPsec中IKE与ISAKMP过程分析(快速模式-消息1)
IPsec中IKE与ISAKMP过程分析(主模式-消息1)_搞搞搞高傲的博客-CSDN博客 IPsec中IKE与ISAKMP过程分析(主模式-消息2)_搞搞搞高傲的博客-CSDN博客 IPsec中IKE与ISAKMP过程分析(主模式-消息3)_搞搞搞高傲的博客…...

PostgreSQL 数据类型转换
各种数据类型(日期/时间、integer、floating point和numeric)转换成格式化的字符串及反过来从格式化的字符串转换成指定的数据类型,在实际操作中经常遇到。下面总结了一些常用的函数。 日期操作函数 函数返回类型描述实例to_char(timestamp…...

【Java笔试强训 1】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🦾🦾🦾 目录 一、选择题 二、编程题 🔥组队竞…...

你买票了吗?五一火车票发售量创历史新高,车票总发售2209万张票
五一劳动节已经成为了除春节国庆节外最隆重的节日,是全国性的庆祝节日。在这个节日里,人们可以通过旅游、购物、娱乐等方式来放松身心,充满活力地迎接新的挑战。同时,五一假期也成为了国内外客流量最大的旅游黄金周之一࿰…...

DiffUtil的使用
RecyclerView的DiffUtil用于计算并更新RecyclerView中数据集的变化。通过使用DiffUtil,我们可以避免完全重新加载整个列表,并且只会更改必要的视图。 以下是DiffUtil的基本用法: 创建一个继承自DiffUtil.Callback的类来计算差异。在这个类中…...

【Python】【进阶篇】18、Django初始化项目环境精讲
目录 18、Django初始化项目环境精讲1. 完成数据库迁移2. PyMySQL模块的使用3. migrate与makemigrations命令详解1) makegrations生成数据库迁移文件2) migrate执行数据库迁移命令3) 完成数据库迁移总结 18、Django初始化项目环境精讲 上一节中,我们完成了对 settin…...

Web前端基础
一.说明 如果你要了解web前端领域,那么三种语言是你必须要了解的,即html5、CSS、Javascript是你必须要了解的,通过前面的专栏内容你一定对html标记语言非常熟悉,那么其他两种语言是什么,他们怎么和html联系在一起&…...

ACM 1007 | 分段函数求值
文章目录 0x00 前言 0x01 题目描述 0x02 问题分析 0x03 代码设计 0x04 完整代码 0x05 运行效果 0x06 总结 0x00 前言 C 语言网不仅提供 C 语言,还包括 C 、 java 、算法与数据结构等课程在内的各种入门教程、视频录像、编程经验、编译器教程及软件下载、题解博…...

ChatGPT技术原理 第十四章:未来发展方向
目录 14.1 多模态对话生成 14.2 跨语言对话生成 14.3 增量学习 14.4 深度强化学习...

大型水利投资集团,打造数智财资管理新范式
随着我国城市化进程的不断推进,城市基础设施在国民经济中的作用愈加重要,其建设水平直接影响一个城市的竞争力。国有城投、水投等企业作为城市基础设施建设的主要参与者,其重要性不言而喻。随着国家、地方对基础设施重要性认识的加深以及政府…...
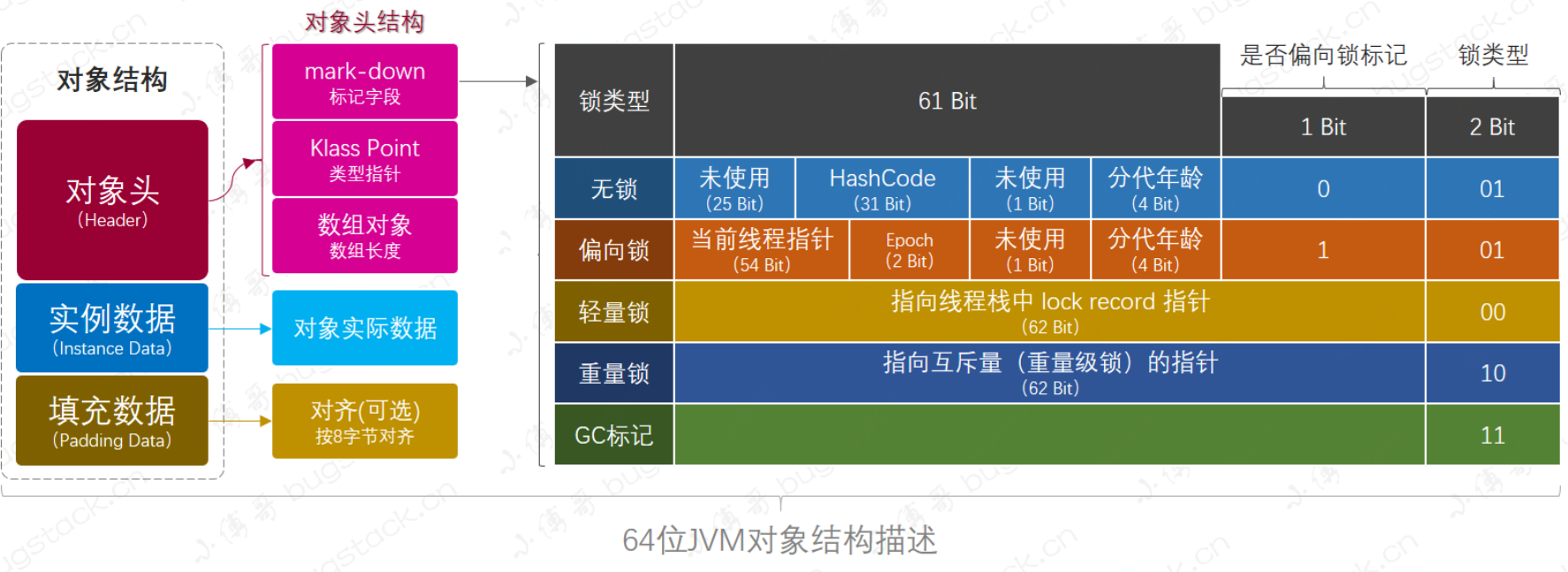
【java】彻底剖析 Synchronized
文章目录 前言对象结构Monitor 对象Synchronized特征原子性可见性有序性可重入锁 锁升级的过程 前言 源码级别剖析Synchronized 对象结构 Synchronized是Java中的隐式锁,它的获取锁和释放锁都是隐式的,完全交由JVM帮助我们操作,在了解Sync…...

有反爬机制就爬不了吗?那是你还不知道反反爬,道高一尺魔高一丈啊
文章目录 一、从用户请求的Headers反爬虫二、基于用户行为反爬虫(1)方法1(2)方法2 三、动态页面的反爬虫四.总结 不知道你们在用爬虫爬数据的时候是否有发现,越来越多的网站都有自己的反爬机制,抓取数据已经…...

手把手教你本地CPU环境部署清华大模型ChatGLM-6B,利用量化模型,本地即可开始智能聊天,达到ChatGPT的80%
大家好,我是微学AI,今天教你们本地CPU环境部署清华大ChatGLM-6B模型,利用量化模型,每个人都能跑动大模型。ChatGLM-6B是一款出色的中英双语对话模型,拥有超过62亿个参数,可高效地处理日常对话场景。与GLM-1…...

FFmpeg 自定义IO CONTEXT实现音频解码,以及seek函数
对于从音频流buffer中解码的场景中,我们需要实现自己的io context 去从buffer中解码,参考ffmepg官方实例:doc/examples/avio_reading.c 关于是否要实现avio context中的seek函数,需要看需要解码什么格式,大部分格式不…...
)
技能升级(2023寒假每日一题 13)
小蓝最近正在玩一款 RPG 游戏。 他的角色一共有 N N N 个可以加攻击力的技能。 其中第 i i i 个技能首次升级可以提升 A i A_i Ai 点攻击力,以后每次升级增加的点数都会减少 B i B_i Bi。 ⌈ A i / B i ⌉ ⌈A_i/B_i⌉ ⌈Ai/Bi⌉(上取整&a…...

低频量化之 可转债 配债数据及策略 - 全网独家
目录 历史文章可转债配债数据 待发转债(进展统计)待发转债(行业统计)待发转债(5证监会通过,PE排序)待发转债(5证监会通过,安全垫排序)待发转债(5证…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
