Python多元线性回归预测模型实验完整版
多元线性回归预测模型
实验目的
通过多元线性回归预测模型,掌握预测模型的建立和应用方法,了解线性回归模型的基本原理
实验内容
多元线性回归预测模型
实验步骤和过程
(1)第一步:学习多元线性回归预测模型相关知识。
一元线性回归模型反映的是单个自变量对因变量的影响,然而实际情况中,影响因变量的自变量往往不止一个,从而需要将一元线性回归模型扩展到多元线性回归模型。
如果构建多元线性回归模型的数据集包含n个观测、p+1个变量(其中p个自变量和1个因变量),则这些数据可以写成下方的矩阵形式:
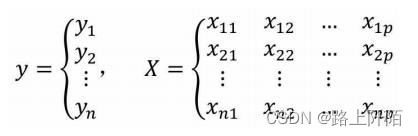
其中,xij代表第个i行的第j个变量值。如果按照一元线性回归模型的逻辑,那么多元线性回归模型应该就是因变量y与自变量X的线性组合,即可以将多元线性回归模型表示成:
y=β0+β1x1+β2x2+…+βpxn+ε
根据线性代数的知识,可以将上式表示成y=Xβ+ε。
其中,
β为p×1的一维向量,代表了多元线性回归模型的偏回归系数;
ε为n×1的一维向量,代表了模型拟合后每一个样本的误差项。
回归模型的参数求解
在多元线性回归模型所涉及的数据中,因变量y是一维向量,而自变量X为二维矩阵,所以对于参数的求解不像一元线性回归模型那样简单,但求解的思路是完全一致的。为了使读者掌握多元线性回归模型参数的求解过程,这里把详细的推导步骤罗列到下方:
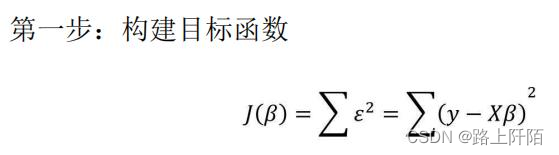
根据线性代数的知识,可以将向量的平方和公式转换为向量的内积,接下来需要对该式进行平方项的展现。


经过如上四步的推导,最终可以得到偏回归系数β与自变量X、因变量y的数学关系。这个求解过程也被成为“最小二乘法”。基于已知的偏回归系数β就可以构造多元线性回归模型。前文也提到,构建模型的最终目的是为了预测,即根据其他已知的自变量X的值预测未知的因变量y的值。
回归模型的预测
如果已经得知某个多元线性回归模型y=β0+β1x1+β2x2+…+βpxn,当有其他新的自变量值时,就可以将这些值带入如上的公式中,最终得到未知的y值。在Python中,实现线性回归模型的预测可以使用predict“方法”,关于该“方法”的参数含义如下:
predict(exog=None, transform=True)
exog:指定用于预测的其他自变量的值。
transform:bool类型参数,预测时是否将原始数据按照模型表达式进行转换,默认为True。
多元线性回归模型是一种统计分析方法,用于研究多个自变量对一个因变量的影响。它是线性回归模型的一种扩展,可以用于解决多个自变量对因变量的影响问题。 在多元线性回归模型中,我们假设因变量 y y y 与 k k k 个自变量 x 1 , x 2 , . . . , x k x_1, x_2, ..., x_k x1,x2,...,xk 之间存在线性关系,即: y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β k x k + ϵ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_k x_k + \epsilon y=β0+β1x1+β2x2+...+βkxk+ϵ 其中 β 0 , β 1 , β 2 , . . . , β k \beta_0, \beta_1, \beta_2, ..., \beta_k β0,β1,β2,...,βk 是模型的系数, ϵ \epsilon ϵ 是随机误差项。我们的目标是通过样本数据来估计模型的系数,从而建立预测模型。 多元线性回归模型的建立可以分为以下几个步骤:
收集数据:收集 n n n 组样本数据,每组数据包括因变量 y y y 和 k k k 个自变量 x 1 , x 2 , . . . , x k x_1, x_2, ..., x_k x1,x2,...,xk 的取值。
数据预处理:对数据进行清洗、缺失值处理、异常值处理等预处理工作,以保证数据的质量。
模型建立:利用最小二乘法等方法,对样本数据进行拟合,求出模型的系数 β 0 , β 1 , β 2 , . . . , β k \beta_0, \beta_1, \beta_2, ..., \beta_k β0,β1,β2,...,βk。
模型评估:通过各种统计指标,如 R 2 R^2 R2、均方误差等,对模型进行评估,判断模型的拟合效果。
模型应用:利用建立好的模型进行预测或分析,得出实际应用价值。 总之,多元线性回归模型是一种重要的统计分析方法,可以用于解决多个自变量对因变量的影响问题,是各种实际问题中常用的建模方法之一。
(2)第二步:数据准备,数据来源于课本例题。
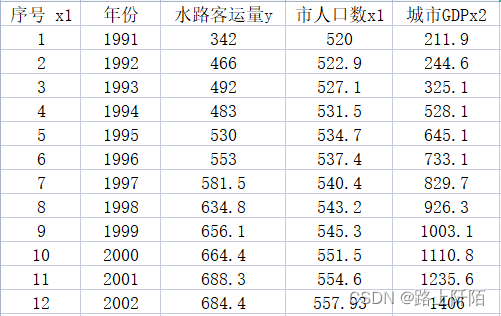
序号 x1 年份 水路客运量y 市人口数x1 城市GDPx2
1 1991 342 520 211.9
2 1992 466 522.9 244.6
3 1993 492 527.1 325.1
4 1994 483 531.5 528.1
5 1995 530 534.7 645.1
6 1996 553 537.4 733.1
7 1997 581.5 540.4 829.7
8 1998 634.8 543.2 926.3
9 1999 656.1 545.3 1003.1
10 2000 664.4 551.5 1110.8
11 2001 688.3 554.6 1235.6
12 2002 684.4 557.93 1406
(3)第三步:使用 Python 编写实验代码并做图。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取Excel文件
data = pd.read_excel('E:\\File\\class\\数据挖掘\\test2.xlsx')
X = data[['市人口数x1', '城市GDPx2']]
y = data['水路客运量y']
# 训练模型
model = LinearRegression()
model.fit(X, y)
# 预测未来水路客运量
x_new = [[560, 1546]]
y_pred = model.predict(x_new)
print("预测未来水路客运量为:", y_pred[0])
print(X)
print(X['市人口数x1'])
# 绘制图像
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
# ax.scatter(X[:, 0], X[:, 1], y)
ax.scatter(X['市人口数x1'], X['城市GDPx2'], y)
# x1, x2 = np.meshgrid(X[:, 0], X[:, 1])
x1, x2 = np.meshgrid(X['市人口数x1'], X['城市GDPx2'])
y_pred = model.predict(np.array([x1.flatten(), x2.flatten()]).T).reshape(x1.shape)
ax.plot_surface(x1, x2, y_pred, alpha=0.5, cmap='viridis')
ax.set_xlabel('市人口数x1')
ax.set_ylabel('城市GDPx2')
ax.set_zlabel('水路客运量y')
plt.title('多元线性回归预测模型案例')
plt.show()代码解释:
上面代码使用了Python中的pandas、numpy、scikit-learn和matplotlib库,实现了一个多元线性回归预测模型的案例。代码的主要功能是读取一个Excel文件中的数据,利用多元线性回归模型对数据进行拟合和预测,最后可视化结果。 具体代码解释如下:
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
首先导入所需的库,包括pandas、numpy、scikit-learn和matplotlib库。其中,LinearRegression类用于实现多元线性回归模型,Axes3D类用于绘制三维图形。
#读取Excel文件
data = pd.read_excel(‘E:\File\class\数据挖掘\test2.xlsx’)
利用pandas库中的read_excel方法读取Excel文件中的数据。
X = data[[‘市人口数x1’, ‘城市GDPx2’]]
y = data[‘水路客运量y’]
将读取到的数据按照自变量和因变量的关系进行划分,X表示自变量,y表示因变量。
#训练模型
model = LinearRegression()
model.fit(X, y)
利用scikit-learn库中的LinearRegression类进行多元线性回归模型的训练,fit方法用于拟合数据。
#预测未来水路客运量
x_new = [[560, 1546]]
y_pred = model.predict(x_new)
print(“预测未来水路客运量为:”, y_pred[0])
利用训练好的模型对新的数据进行预测,predict方法用于预测。输出预测结果。
print(X)
print(X[‘市人口数x1’])
输出自变量的数据。
#绘制图像
fig = plt.figure()
ax = fig.add_subplot(projection=‘3d’)
#ax.scatter(X[:, 0], X[:, 1], y)
ax.scatter(X[‘市人口数x1’], X[‘城市GDPx2’], y)
#x1, x2 = np.meshgrid(X[:, 0], X[:, 1])
x1, x2 = np.meshgrid(X[‘市人口数x1’], X[‘城市GDPx2’])
y_pred = model.predict(np.array([x1.flatten(), x2.flatten()]).T).reshape(x1.shape)
ax.plot_surface(x1, x2, y_pred, alpha=0.5, cmap=‘viridis’)
ax.set_xlabel(‘市人口数x1’)
ax.set_ylabel(‘城市GDPx2’)
ax.set_zlabel(‘水路客运量y’)
plt.title(‘多元线性回归预测模型案例’)
plt.show()
这一部分是绘制一个三维图形,其中fig是一个Figure对象,ax是一个Axes3D对象。首先用scatter方法绘制出原始数据点的三维散点图,然后用meshgrid方法将自变量的取值进行网格化,用predict方法预测出因变量的取值,最后用plot_surface方法绘制出三维图形。常用的参数有:alpha表示透明度,cmap表示颜色映射,set_xlabel、set_ylabel和set_zlabel分别表示三个坐标轴的标签,title表示图形的标题。最后调用show方法显示图形。
(4)第四步:实验结果。
绘图和预测当市人口数x1为560以及城市GDPx2为1546时的水路客运量y。
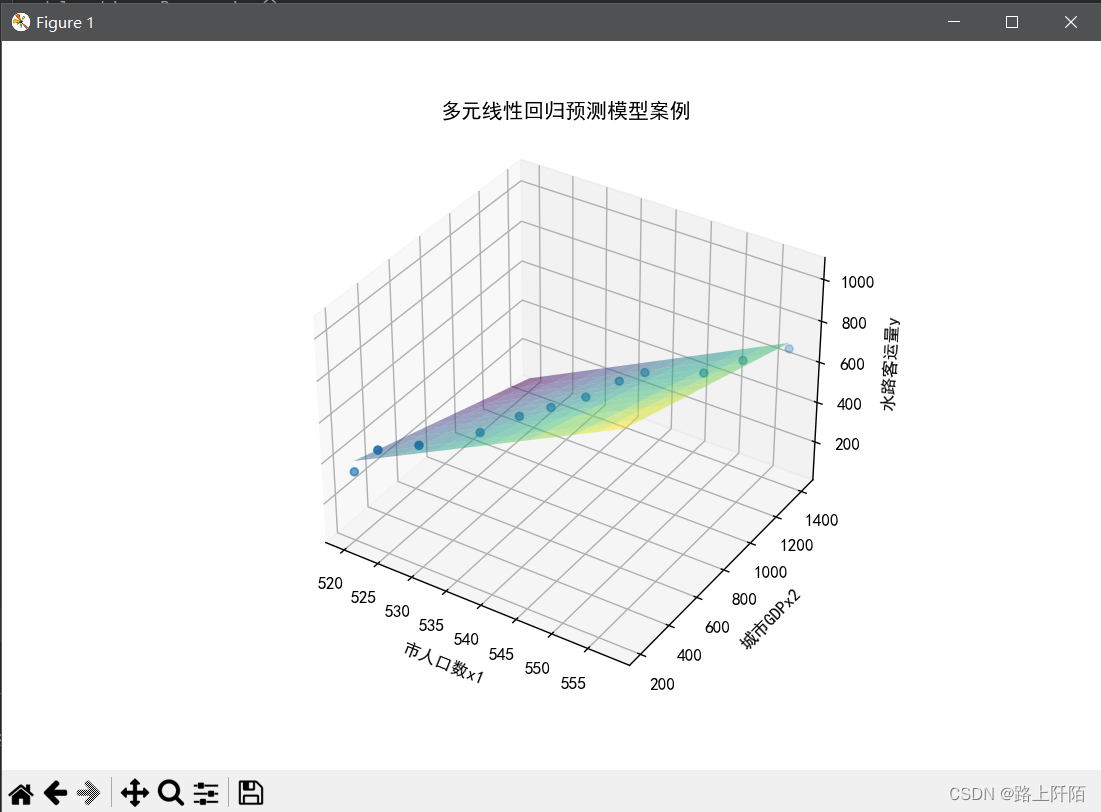
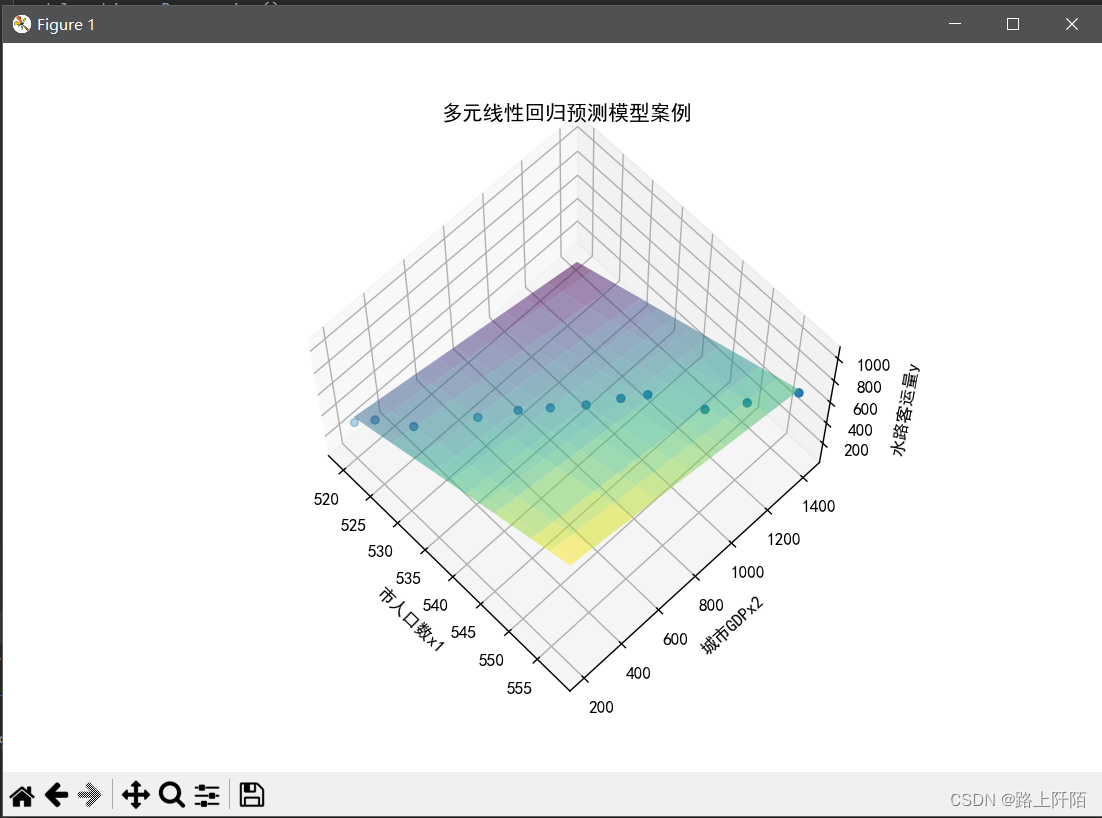

这里的预测结果为:711.2940429652463
实验总结
通过本次实验,我学习了多元线性回归预测模型的基本原理和建立方法,了解了如何使用Python编程实现预测模型。同时,我们也使用水路客运量预测实例,对线性回归模型进行了实际应用和分析。在实验中,我掌握了数据预处理、模型训练和结果评估等关键技术,对于今后的数据分析和预测工作将有很大的帮助。同时在这个过程之中也出现了一些问题,但通过查阅相关资料最终这些问题都得以解决。在这个过程中我的动手实践能力的到提升,也让我明白了实际动手操作的重要性,在实际操作中可以发现很多平时发现不了的问题,通过实践最终都得以解决。
相关文章:

Python多元线性回归预测模型实验完整版
多元线性回归预测模型 实验目的 通过多元线性回归预测模型,掌握预测模型的建立和应用方法,了解线性回归模型的基本原理 实验内容 多元线性回归预测模型 实验步骤和过程 (1)第一步:学习多元线性回归预测模型相关知识。 一元线性回归模型…...

C#基础 变量在内存中的存储空间
变量存储空间(内存中) // 1byte 8bit // 1KB 1024byte // 1MB 1024KB // 1GB 1024MB // 1TB 1024GB // 通过sizeof方法 可以获取变量类型所占的内存空间(单位:字节) 有…...

你最关心的4个零代码问题,ChatGPT 帮你解答了!
作为人工智能(AI)新型聊天机器人模型 ChatGPT,刚上线5天就突破100万用户,两个多月全球用户量破亿,不愧为业界最炙热的当红炸子鸡。 ChatGPT 是一种语言生成模型,由 OpenAI 开发和训练。它是基于 Transform…...

linux的环境变量
目录 一、自定义变量和环境变量的区别 二、自定义变量 三、环境变量 四、查看所有变量(自定义变量、环境变量) 五、记录环境变量到相关的系统文件 (1)为什么要这样做? (2)环境变量相关系统…...
openQA----基于openSUSE部署openQA
【原文链接】openQA----基于openSUSE部署openQA (1)下载 openqa-bootstrap 脚本并执行 cd /opt/ curl -s https://raw.githubusercontent.com/os-autoinst/openQA/master/script/openqa-bootstrap | bash -x(2)配置apache proxy…...
正则表达式基础一
BRE(basic regular expression):匹配数据流中的文本字符 普通文本匹配 特殊字符 正则表达式存在一些特殊字符,如需当成普通文本来匹配,必须加上转义,即反斜杠\,如下所示 .*[]^${}?|() 指定出现位置的字符 ^ 指定行首…...

Java中的内存泄露、内存溢出与栈溢出
内存泄露、内存溢出与栈溢出 1、概述2、内存泄漏、内存溢出和栈溢出2.1、内存泄漏2.2、内存溢出2.3、栈溢出 2、总结 1、概述 大家好,我是欧阳方超。本次就Java中几个相似而又不同的概念做一下介绍。内存泄漏、内存溢出和栈溢出都是与内存相关的问题,但…...

时序预测 | Matlab实现SSA-GRU、GRU麻雀算法优化门控循环单元时间序列预测(含优化前后对比)
时序预测 | Matlab实现SSA-GRU、GRU麻雀算法优化门控循环单元时间序列预测(含优化前后对比) 目录 时序预测 | Matlab实现SSA-GRU、GRU麻雀算法优化门控循环单元时间序列预测(含优化前后对比)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现SSA-GRU、GRU麻雀算法…...

Java+springboot开发的医院HIS信息管理系统实现,系统部署于云端,支持多租户SaaS模式
一、项目技术框架 前端:AngularNginx 后台:JavaSpring,SpringBoot,SpringMVC,SpringSecurity,MyBatisPlus,等 数据库:MySQL MyCat 缓存:RedisJ2Cache 消息队列&…...

【前端面经】Vue-Vue中的 $nextTick 有什么作用?
Vue.js 是一个流行的 JavaScript 框架,它提供了许多实用的功能,其中之一就是 $nextTick 方法。 在 Vue.js 中, $nextTick 方法可以确保我们在更新 DOM 之后再去执行某些操作,从而避免由于 DOM 更新而导致的问题。这个方法非常实用…...
基于STATCOM的风力发电机稳定性问题仿真分析(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

如何写出高质量的代码
背景说明: 你是否曾经为自己写的代码而感到懊恼?你是否想过如何才能写出高质量代码?那就不要错过这个话题!在这里,我们可以讨论什么是高质量代码,如何写出高质量代码等问题。无论你是初学者还是资深开发人…...
15.基于主从博弈的智能小区代理商定价策略及电动汽车充电管理
说明书 MATLAB代码:基于主从博弈的智能小区代理商定价策略及电动汽车充电管理 关键词:电动汽车 主从博弈 动态定价 智能小区 充放电优化 参考文档:《基于主从博弈的智能小区代理商定价策略及电动汽车充电管理》基本复现 仿真平台&#…...

ChatGPT实现多语种翻译
语言翻译 多语种翻译是 NLP 领域的经典话题,也是过去很多 AI 研究的热门领域。一般来说,我们认为主流语种的互译一定程度上属于传统 AI 已经能较好完成的任务。比如谷歌翻译所采用的的神经机器翻译(NMT, Neural Machine Translation)技术就一度让世人惊…...

volatile关键字原理的使用介绍和底层原理解析和使用实例
文章目录 volatile关键字原理的使用介绍和底层原理解析和使用实例1. volatile 关键字的作用2. volatile 的底层原理3. volatile 的使用案例4. volatile 的原子性问题5. 如何解决 volatile 的原子性问题6. volatile 的实现原理7. 小结8. volatile的最佳实践9. 案例:使用volatile…...
【软件下载】换新电脑记录下下载的软件时所需地址
1.idea https://www.jetbrains.com/zh-cn/idea/download/other.html 2.oracle官方(下载jdk时找的) https://www.oracle.com/ 3.jdk8 https://www.oracle.com/java/technologies/downloads/ 下拉找到jdk8 切换windows (需要注册个oracle账…...

【10.HTML入门知识-CSS元素定位】
1 标准流(Normal Flow) 默认情况下,元素都是按照normal flow(标准流、常规流、正常流、文档流【document flow】)进行排布 从左到右、从上到下按顺序摆放好 默认情况下,互相之间不存在层叠现象 1.1…...

LeetCode_贪心算法_简单_455.分发饼干
目录 1.题目2.思路3.代码实现(Java) 1.题目 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的…...

HashMap
目录 HashMap是什么? 为什么要使用HashMap? HashMap存储元素原理(put⽅法) 扰动函数 前置知识 异或运算 &运算 为什么使用扰动函数 实验验证扰动函数 常见问题 HashMap的默认长度是多少? HashMap是先扩…...
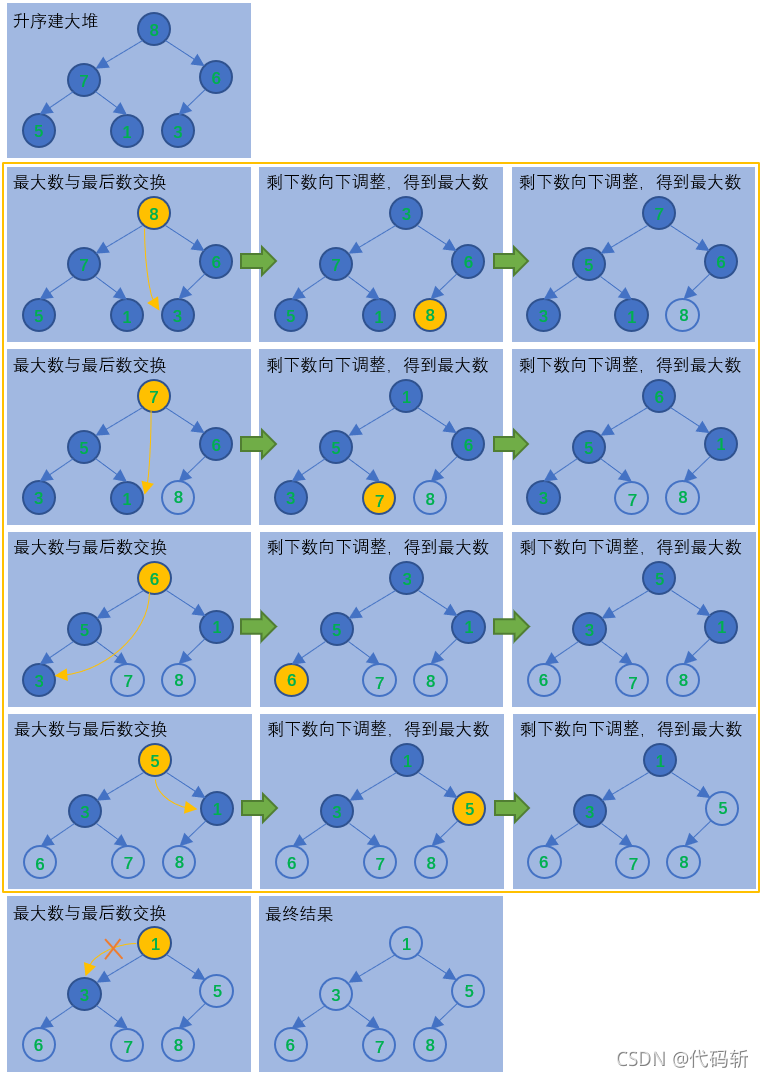
数据结构初阶 —— 树(堆)
目录 一,堆 堆的概念 向下调整法(数组) 向上调整法(数组) 堆的创建(建堆) 堆的实现 一,堆 堆的概念 如有个关键码的集合K{,,,...…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
