《程序员面试金典(第6版)面试题 16.09. 运算
题目描述
请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。
你的实现应该支持如下操作:
- Operations() 构造函数
- minus(a, b) 减法,返回a - b
- multiply(a, b) 乘法,返回a * b
- divide(a, b) 除法,返回a / b
示例:
Operations operations = new Operations();
operations.minus(1, 2); //返回-1
operations.multiply(3, 4); //返回12
operations.divide(5, -2); //返回-2
提示:
- 你可以假设函数输入一定是有效的,例如不会出现除法分母为0的情况
- 单个用例的函数调用次数不会超过1000次
解题思路与代码
-
这道题属实是一道中等难度的题。需要你有一定的思考量,才可以做出来。
-
题目的要求是,
不允许我们使用位运算符,除了 + 法以外的算术运算符,去实现两个数之间的减法,乘法,除法函数。 -
也就是说,我们可以使用 + 法运算符,关系运算符(==, <= , >=, < , >)还有逻辑运算符 ( ! , && , ||)去实现这些函数。
-
这道题建议大家不要抖机灵,使用各种没有意义的库函数来简便运算。还有这道题也不要去使用vector这种数据结构。因为,
vector的模板类在实现时涉及到位运算符和减法运算符的。
接下来,其实我们就要思考一个问题。乘法,除法的本质是什么?
- 那其实是不是就是加法(乘法的本质是加法)与减法(除法的本质是减法)呢?
- 那也就是说,要实现除法函数,首先得实现减法函数。
那我们,在来思考一个问题,减法的本质是什么?
- 那是不是加上一个相反数呢?
- 所以要实现减法函数,首先我们还需要去实现一个取反函数。
其实这道题还有一个隐藏的条件,那就是提示:单个用例的函数调用次数不会超过1000次。
- 也就是说,这道题,出题人不想你太容易去解决这个问题。问你如何优化流程,也就是缩短时间复杂度。
- 假如说我们要用累加去实现取反过程,你想想时间复杂度是不是O(n),那有没有一种办法可以优化累加的时间复杂度呢?
- 当然有。我们可以通过事先创建两个数组,分别去存储正负2的多少次方的值是多少。到时候,我们可以用循环的方式,去累加预定值,这样是不是就将时间复杂度O(n)缩短到O(logn)了呢?
OK,这道题讲到这里,大家应该心里很有谱了才对。做这道题,首先,我们要创建两个内置数组,去存储可能出现的2的次方值。然后先实现取反函数。再实现减法函数,再实现乘法函数,最后实现除法函数。
实现的过程中,需要大家注意溢出问题。因为虽然题目给的值的范围不会超过int的最大最小范围。但是两个数相减,相乘,相除的过程中,如果处理不好,是会发生溢出问题的。
具体的实现请看代码:
class Operations {int posN[31]; // 放正数2的n次方int negN[31]; // 放负数2的n次方//取相反数函数int oppN(int num){if(!num) return 0;int res = 0;if(num > 0){ // 从2^30次方开始检查for(int i = 30; i >= 0; i += (-1)){if(num + negN[i] < 0) continue;num += negN[i];res += negN[i];}}else{ // 从 - 2^30次方开始检查for(int i = 30; i >= 0; i += (-1)){if(num + posN[i] > 0) continue;num += posN[i];res += posN[i];}}return res;}
public:Operations() {int p = 1;int n = -1;posN[0] = p;negN[0] = n;// 初始化次方数组for(int i = 1; i < 31; ++i){p += p;posN[i] = p;n += n;negN[i] = n;}}int minus(int a, int b) {return a + oppN(b);}int multiply(int a, int b) {if(!a || !b) return 0;if(a == 1) return b;if(b == 1) return a;if(b < 0) return oppN(multiply(a,oppN(b))); // 统一b的正负int res = a;int count = 1;while(count < posN[30] && count + count <= b ){res += res;count += count;}res += multiply(a,minus(b,count));return res;}int divide(int a, int b) {if(!a) return 0;int res = 1;if(a > 0){if(b == INT_MIN) return 0;if(b < 0) return oppN(divide(a,oppN(b))); // 统一a,b的正负if(a < b) return 0;int count = b;while(count < posN[30] && a >= count + count){res += res;count += count;}res += divide(minus(a,count),b);}else{if(b == 1) return a;if(b > 0) return oppN(divide(a,oppN(b)));if(a > b) return 0;int count = b;while(count >= negN[30] && a <= count + count){res += res;count += count;}res += divide(minus(a,count),b);}return res;}
};
复杂度分析
下面是这个代码中各个函数的时间复杂度和空间复杂度分析:
-
oppN(int num):时间复杂度为 O(log(num)),因为它在最坏情况下需要遍历数组 posN 或 negN 中的所有元素(共 31 个),这与输入数字的二进制表示长度成正比。空间复杂度为 O(1),因为它使用了固定数量的额外存储空间。
-
Operations() 构造函数:时间复杂度为 O(1),因为它只需要遍历 31 个元素并执行一定数量的操作。空间复杂度为 O(1),因为它只使用了固定大小的 posN 和 negN 数组。
-
minus(int a, int b):时间复杂度为 O(log(b)),因为它调用了 oppN 函数。空间复杂度为 O(1),因为它没有使用额外的存储空间。
-
multiply(int a, int b):时间复杂度为 O(log(a) * log(b)),因为它使用递归实现,每次递归调用都会减小 b 的值,递归深度为 O(log(b)),而每次递归调用都会调用 minus 函数,时间复杂度为 O(log(a))。空间复杂度为 O(log(b)),因为递归深度与空间复杂度成正比。
-
divide(int a, int b):时间复杂度为 O(log(a) * log(b)),因为它也是使用递归实现,每次递归调用都会减小 a 的值,递归深度为 O(log(a)),而每次递归调用都会调用 minus 函数,时间复杂度为 O(log(b))。空间复杂度为 O(log(a)),因为递归深度与空间复杂度成正比。
总的来说,这个实现的时间复杂度主要取决于输入数字的二进制表示长度,而空间复杂度主要取决于递归深度。
总结
-
这道题的意义在于考察编程能力、逻辑思维和对基本运算的理解。 -
它要求我们在限制条件下(仅使用加法运算符和逻辑运算符)实现整数数字的减法、乘法和除法运算。这种问题有助于锻炼思考能力,强化对计算机基本原理的理解,以及提高解决问题的灵活性。
-
同时,这种问题也有助于理解计算机是如何处理基本的算术运算的,以及为什么某些优化方法(例如位运算)是有效的。通过解决这种问题,你可以加深对计算机科学和编程原理的理解。
-
最后的最后,如果你觉得我的这篇文章写的不错的话,请给我一个赞与收藏,关注我,我会继续给大家带来更多更优质的干货内容。
相关文章:

《程序员面试金典(第6版)面试题 16.09. 运算
题目描述 请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。 你的实现应该支持如下操作: Operations() 构造函数minus…...

asp.net基于web的校园美食派送配送系统
1.系统登录:系统登录是用户访问系统的路口,设计了系统登录界面,包括用户名、密码和验证码,然后对登录进来的用户判断身份信息,判断是管理员用户还是普通用户。 2.系统用户管理:不管是…...

【JAVA】#详细介绍!!! 文件操作之File对象(1)!
本文内容不涉及文件内容操作,主要是对指定文件元信息的获取,以及通过java代码如何创建一个文件或者删除文件 目录 文件操作的File对象 File对象的基本操作方法 得到文件(夹)对象的信息元 1.getParent 2. getName 3.getPath 4…...

Vue基本的内置指令
前言 除了常见的v-bind,v-for,v-if,v-on.v-model等,本次学习一些vue提供的其他内置指令 1 v-text 给标签插入文本,类似于插值语法 它会把全部的字符串当成文本去解析,不会当成标签的,哪怕写的是标签结构 效果和插值语法是一样的 插值语法比v-text更加…...

华为孟晚舟当值首秀:2030年AI算力将增长500倍!
作者 | 范智林 来源 | 华商观察 微信号:HuashangGC 孟晚舟当值首次亮相。 4月19日,华为副董事长、轮值董事长、CFO孟晚舟在华为第20届全球分析师大会上进行演讲,这是她当值华为轮值董事长以来的首次公开亮相。 按照华为内部规定,…...

关于python异常的总结
Python异常是在程序执行时发生的错误,可能会导致程序终止运行。 在Python中,异常处理是一种机制,它允许开发人员在程序发生异常时捕获、处理和报告这些异常,以便程序可以继续运行或在出现异常时进行优雅的退出。 在Python中&…...
基于Java+SpringBoot+vue学生学习平台详细设计实现
基于JavaSpringBootvue学生学习平台详细设计实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方式 文章目…...

【云原生网关】Kong 使用详解
目录 一、前言 二、Kong介绍 三、Kong核心组件 3.1 kong组件介绍 3.1.1 Kong Server 3.1.2 Apache Cassandra/PostgreSQL 3.1.3 Kong dashboard 3.2 传统网关与Kong工作模式对比 四、Kong网关特征与架构 4.1 kong网关特征 4.1.1 可扩展性 4.1.2 模块化 4.1.3 在任…...

浅谈之Java多线程
Java多线程是Java语言中一个非常重要的特性,它允许程序同时执行多个任务。通过多线程,程序可以同时处理多项任务,从而缩短程序的执行时间。另外,多线程也有助于利用多核处理器,更好地发挥计算机硬件的性能。 那我们在…...

【Vue3学习笔记1】一个清单应用帮你入门Vue.js
Vue 目前已经是国内最流⾏的前端框架之⼀,Vue 3 带来的诸多优化更是让前端圈迎来了新的潮流,比如: 基于 Proxy 的全新响应式实现; Composition API <script setup> 组织代码的更优方式; 更有料的 TypeScript 支…...

go破冰之旅·8·go函数基本实践及各种玩法
一次5-10分钟即可搞定,以干货效率的学习方式带你更直观的玩转各种玩法! 行文不易,一字一句纯手打创造,倾注了不少精力,感谢支持。 目录 什么是函数?有哪些元素? 函数参数、返回值 小程序&…...
Qt - 从零到壹的 打地鼠 游戏
❤️🔥欢迎收看西北风的blog,好男人就是我,我就是西北风。✨ Gitee 地址 W_A_Mole NTC_jason/cc语言 - 码云 - 开源中国 (gitee.com) 目录 🟥一:创建一个主窗体 🟣二.:添加主窗口背景图片…...
代码自动发布系统
之前是jenkins发现gitlab代码更新了就自动获取直接部署到服务器 现在是jenkins自动获取Code之后打包成镜像上传到仓库然后通知docker去拉取更新的镜像 分析 旧∶ 代码发布环境提前准备,以主机为颗粒度静态 新: 代码发布环境多套,以容器为颗粒度编译 …...
——安装)
qemu-基础篇(一)——安装
文章目录 env安装查看版本查看支持的开发板查看支持的CPU的型号 env ubuntu 安装 sudo apt-get install qemu sudo apt-get install qemu-system-arm sudo apt-get install qemu-system查看版本 qemu-img -V qemu-system-arm --version qemu-system-aarch64 --version返回结…...
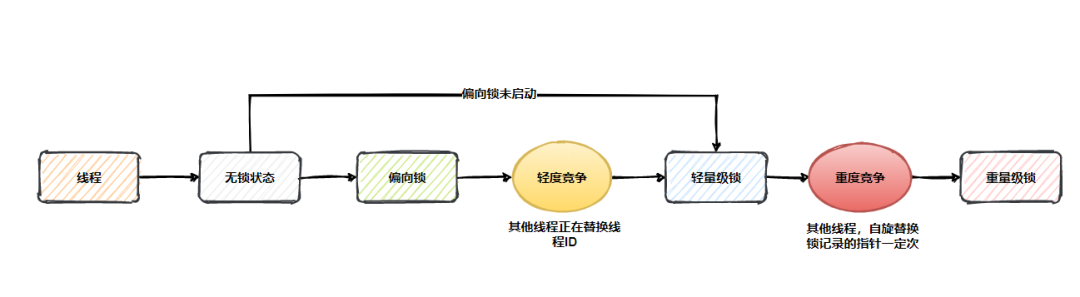
从根本上理解Synchronized的加锁过程
作为一个Java开发,对于Synchronized这个关键字并不会陌生,无论是并发编程,还是与面试官对线,Synchronized可以说是必不可少。 在JDK1.6之前,都认为Synchronized是一个非常笨重的锁,就是在之前的《谈谈Java…...
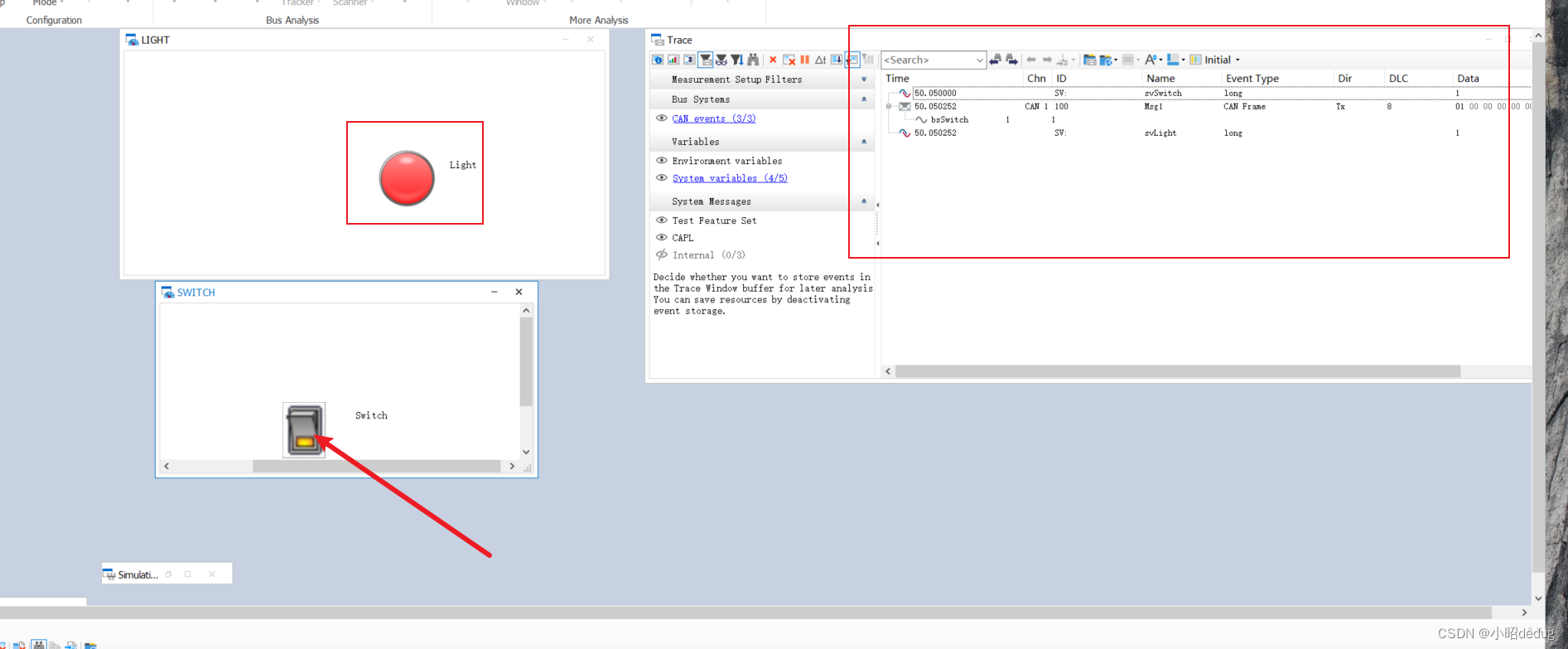
CANOE入门到精通——CANOE系列教程记录1 第一个仿真工程
本系列以初学者角度记录学习CANOE,以《CANoe开发从入门到精通》参考学习,CANoe16 demo版就可以进行学习 概念 CANoe是一种用于开发、测试和分析汽车电子系统的软件工具。它通过在不同层次上模拟汽车电子系统中的不同部件,如ECU、总线和传感…...

JavaEE——单例模式
文章目录 一、介绍什么是单例模式二、饿汉模式三、懒汉模式四、讨论两种模式的线程安全问题 一、介绍什么是单例模式 在介绍单例模式之前,我们得先明确一个名词设计模式。 所谓设计模式其实不难理解,就是在计算机这个圈子中,呢些大佬们为了…...

关于数据倾斜
1、数据倾斜表现 1.1 hadoop中的数据倾斜表现 有一个多几个Reduce卡住,卡在99.99%,一直不能结束。各种container报错OOM异常的Reducer读写的数据量极大,至少远远超过其它正常的Reducer伴随着数据倾斜,会出现任务被kill等各种诡异…...

Shell第一次作业
要求: 1、判断当前磁盘剩余空间是否有20G,如果小于20G,则将报警邮件发送给管理员,每天检查一次磁盘剩余空间。 2、判断web服务是否运行(1、查看进程的方式判断该程序是否运行,2、通过查看端口的方式判断…...
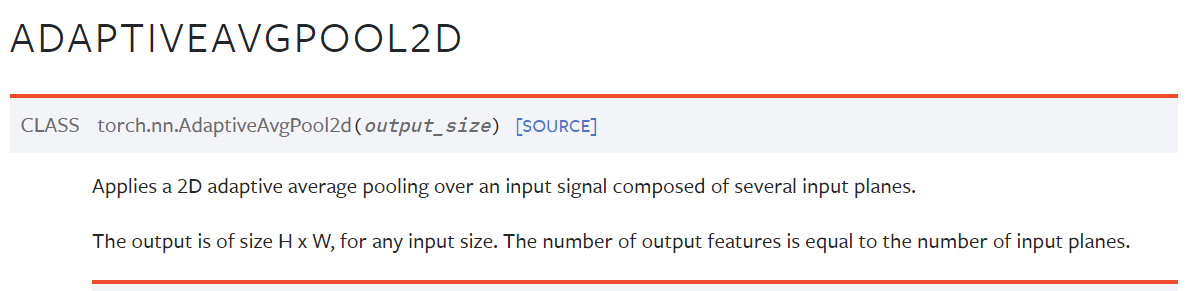
实例解读nn.AdaptiveAvgPool2d((1, 1))
nn.AdaptiveAvgPool2d((1, 1))在PyTorch中创建一个AdaptiveAvgPool2d类的实例。该类在输入张量上执行2D自适应平均池化。 自适应平均池化是一种池化操作,它计算每个输入子区域的平均值并产生一个指定大小的输出张量。子区域的大小是根据输入张量的大小和输出张量的…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
