算法记录 | 48 动态规划
198.打家劫舍
思路:
1.确定dp数组(dp table)以及下标的含义:dp[i]:前 i 间房屋所能偷窃到的最高金额。
2.确定递推公式:dp[i] = max(dp[i - 2] + nums[i-1], dp[i - 1])
i间房屋的最后一个房子是nums[i−1]。
如果房屋数大于等于 2 间,则偷窃第 i−1 间房屋的时候,就有两种状态:
-
偷窃第 i−1 间房屋,那么第 i-2 间房屋就不能偷窃了,偷窃的最高金额为:前 i−2 间房屋的最高总金额 + 第 i−1 间房屋的金额,即 dp[i]=dp[i−2]+nums[i-1];
-
不偷窃第 i−1 间房屋,那么第 i−2 间房屋可以偷窃,偷窃的最高金额为:前 i−1 间房屋的最高总金额,即 dp[i]=dp[i−1]。
-
初始条件:
-
前 0 间房屋所能偷窃到的最高金额为 0,即 dp[0]=0。
-
前 1 间房屋所能偷窃到的最高金额为 nums[0],即:dp[1]=nums[0]。
-
-
确定遍历顺序:dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历
class Solution:def rob(self, nums: List[int]) -> int:size = len(nums)if size == 0:return 0dp = [0 for _ in range(size + 1)]dp[0] = 0dp[1] = nums[0]for i in range(2, size + 1):dp[i] = max(dp[i - 2] + nums[i - 1], dp[i - 1])return dp[size]
213.打家劫舍II
思路:
这道题可以看做是「198. 打家劫舍」的升级版。
如果房屋数大于等于 3 间,偷窃了第 1 间房屋,则不能偷窃最后一间房屋。同样偷窃了最后一间房屋则不能偷窃第 1 间房屋。
假设总共房屋数量为size,这种情况可以转换为分别求解 [0,size−2] 和 [1,size−1] 范围下首尾不相连的房屋所能偷窃的最高金额,然后再取这两种情况下的最大值。而求解 [0,size−2] 和 [1,size−1] 范围下首尾不相连的房屋所能偷窃的最高金额问题就跟「198. 打家劫舍」所求问题一致了。
class Solution:def helper(self, nums):size = len(nums)if size == 0:return 0dp = [0 for _ in range(size + 1)]dp[0] = 0dp[1] = nums[0]for i in range(2, size + 1):dp[i] = max(dp[i - 2] + nums[i - 1], dp[i - 1])return dp[size]def rob(self, nums: List[int]) -> int:size = len(nums)if size == 1:return nums[0]ans1 = self.helper(nums[:size - 1])ans2 = self.helper(nums[1:])return max(ans1, ans2)
337.打家劫舍III
思路:
树形动态规划问题。
对于当前节点 cur,不能选择子节点,也不能选择父节点。所以对于一棵子树来说,有两种情况:
- 选择了根节点
- 没有选择根节点
1.选择根节点
如果选择了根节点,则不能再选择左右儿子节点,这种情况下的最大值为:当前节点 + 左子树不选择根节点 + 右子树不选择根节点。
不选择根节点
2.如果不选择根节点,则可以选择左右儿子节点,共四种可能:
- 左子树选择根节点 + 右子树选择根节点
- 左子树选择根节点 + 右子树不选根节点
- 左子树不选根节点 + 右子树选择根节点
- 左子树不选根节点 + 右子树不选根节点
选择其中最大值。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:# dp数组(dp table)以及下标的含义:# 1. 下标为 0 记录 **不偷该节点** 所得到的的最大金钱# 2. 下标为 1 记录 **偷该节点** 所得到的的最大金钱dp = self.traversal(root)return max(dp)# 要用后序遍历, 因为要通过递归函数的返回值来做下一步计算def traversal(self, node):# 递归终止条件,就是遇到了空节点,那肯定是不偷的if not node:return (0, 0)left = self.traversal(node.left)right = self.traversal(node.right)# 不偷当前节点, 偷子节点val_0 = max(left[0], left[1]) + max(right[0], right[1])# 偷当前节点, 不偷子节点val_1 = node.val + left[0] + right[0]return (val_0, val_1)
相关文章:

算法记录 | 48 动态规划
198.打家劫舍 思路: 1.确定dp数组(dp table)以及下标的含义:dp[i]:前 i 间房屋所能偷窃到的最高金额。 2.确定递推公式:dp[i] max(dp[i - 2] nums[i-1], dp[i - 1]) i间房屋的最后一个房子是nums[i−…...

CRM部署Always on 后 CRM报无法更新数据库,数据库只读,且读写分离不正常
CRM部署Always on 后 CRM报无法更新数据库,数据库只读,读写分离不正常 问题描述背景信息问题原因解决方案 问题描述 CRM部署Always on 后 CRM报无法更新数据库,数据库只读 读写分离不正常,出现错乱链接。 背景信息 1.2个节点配置SQL serve…...

麓言信息设计创意思维,打开设计师思路
在现在快速发展的时代,信息纷杂繁琐,如果一个设计不能让人眼前一亮,印象深刻,只会沦为平凡作品,无亮点无用处。正所谓,无设计不创意,这句口号正是喊出对设计的要求。 伴随着时代的发展、…...

POJ3704 括号匹配问题 递归方法
目录 题目 算法 完整代码 题目 参考 递归: https://blog.csdn.net/qq_45272251/article/details/103257953 利用了递归, 但思路稍复杂了 循环: https://blog.csdn.net/weixin_50340097/article/details/114579805 (看起来是递归其实是循环. 每次递归其实是循环内一次迭…...
:完全相等的 JSON 字符串、复合函数、 分组、柯里化、将对象转换为 JSON 字符串)
leetcode — JavaScript专题(三):完全相等的 JSON 字符串、复合函数、 分组、柯里化、将对象转换为 JSON 字符串
专栏声明:只求用最简单的,容易理解的方法通过,不求优化,不喜勿喷 2628. 完全相等的 JSON 字符串 题面 给定两个对象 o1 和 o2 ,请你检查它们是否 完全相等 。 对于两个 完全相等 的对象,它们必须包含相…...

OGNL 的表达式
目录 概念 基本原理 基本语法 1、访问Root区域对象基本语法 2、访问Context区域对象基本语法 符号含义 概念 Object-Graph Navigation Language 对象-图形导航语言, 主要用于访问对象的数据和方法。 基本原理 主要由3部分构成:1.OGNL引擎 …...

JAVA面试中遇到的那些坑,80%的人都种过招
面试,是很多学完Java开发的人不得不面对的问题。小编经常听到学员抱怨,明明觉得自己学的不错,为什么到了面试的时候就凉凉了?为什么有的面试官会一直问业务层面的问题,让人措手不及? 其实,我们在学习Java知识的同时…...

【测试开发】单元测试、基准测试和性能分析(以 Go testing 为例)
一、为什么需要测试🤔️ 你写不出 bug-free 的代码。你认为自己写出了 bug-free 的代码,但它在你意想不到的地方出错了。你觉得自己写出了永不出错的代码,但它的性能十分糟糕。 二、在开发过程中做好测试(理想情况下)…...

linux中一条命令查询当前端口的进程,然后拿到进程pid,作为另一条杀死进程的参数
1. 可以使用lsof命令来查询端口对应的进程,然后使用awk命令提取PID,最后将其作为另一条命令的参数。 例如,如果要查询端口为8080的进程: lsof -i :8080 | awk NR2{print $2}其中,-i选项指定查询网络连接,…...

程序员找工作难吗?我用亲身经历来告诉大家
我看到很多同学说今年的程序员找工作难。我的心里也有一定预期,但直到我出来之后才真正地感受到这股寒冬有多么凛冽。 一个外包公司有四五个招聘人员,然后外包公司有十来个,一个公司的岗位会分发给这些各个不同的外包公司。所以你看到我沟通…...
【Web服务】HTTP和DNS重要知识
304状态码 HTTP状态码中的304状态码表示"未修改",通常在客户端发起了一个带有If-Modified-Since头部的GET请求时会得到这个响应。服务器通过比较If-Modified-Since头部指定的时间戳和资源的最后修改时间来判断资源是否被修改过,如果没有修改则…...

【C++】-关于类和对象的默认成员函数(中)-拷贝构造函数和赋值运算符重载函数
💖作者:小树苗渴望变成参天大树 ❤️🩹作者宣言:认真写好每一篇博客 💨作者gitee:gitee 💞作者专栏:C语言,数据结构初阶,Linux,C 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点…...
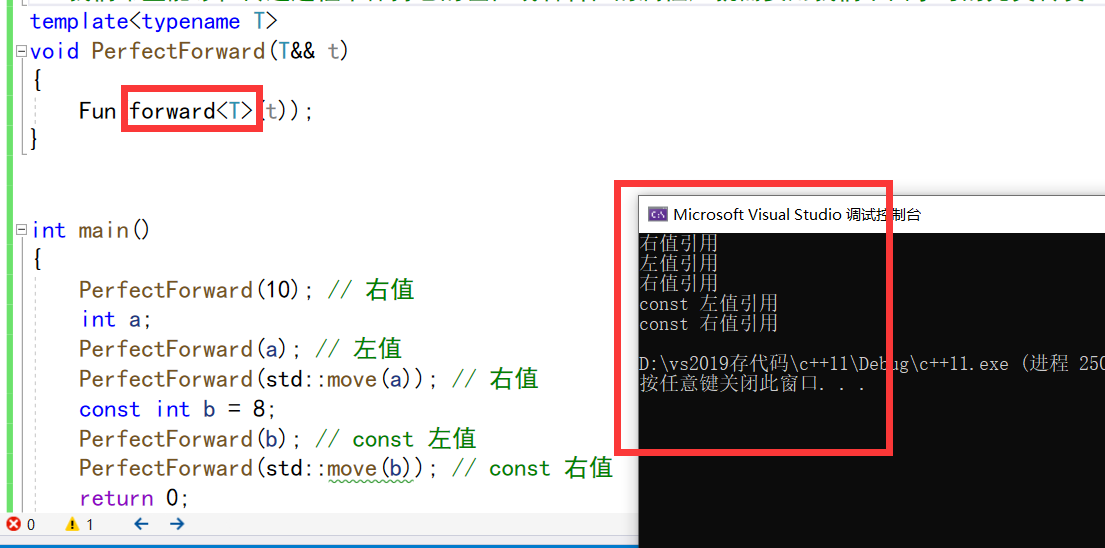
c++11上篇
c11 1.C11简介2.列表初始化2.1 {}初始化2.2 std::initializer_list 3.变量类型推导3.1 auto3.2 decltype3.3 nullptr 4.范围for循环5.final与override6.智能指针7.新增加容器---静态数组array、forward_list以及unordered系列8.默认成员函数控制9.右值引…...
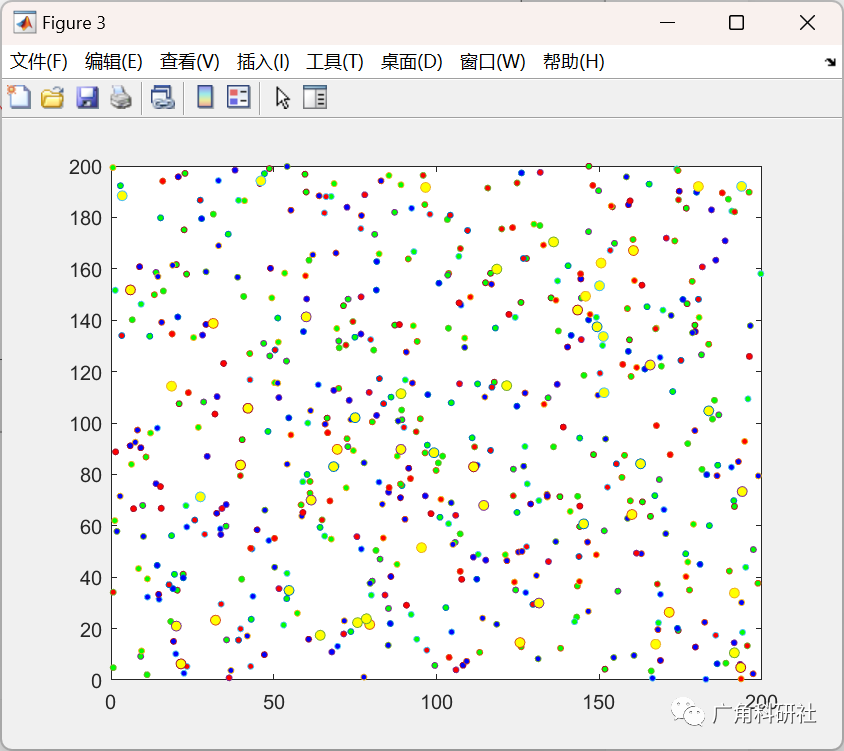
异构无线传感器网络路由算法研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 无线传感器网络(Wireless Sensor Networks, WSN)是一种新型的融合传感器、计算机、通信等多学科的信息获取和处理技术的网络,…...

MySQL数据库——MySQL TRUNCATE:清空表记录
MySQL 提供了 DELETE 和 TRUNCATE 关键字来删除表中的数据。下面主要讲解一下 TRUNCATE 关键字的使用。 TRUNCATE 关键字用于完全清空一个表。其语法格式如下: TRUNCATE [TABLE] 表名 其中,TABLE 关键字可省略。 例 1 新建表 tb_student_course&…...

财报解读:连续三年逆势增长的背后,欧派家居到底靠的是什么?
能在过去3年逆势增长的家居企业并不多,而欧派家居就是其中一个。4月25日,欧派家居发布2022年年度报告。据年报数据显示,2022年,欧派家居共实现营业收入224.80亿元,净利润约26.88亿元。 从2020年到2022年,欧…...

希望计算机专业同学都知道这些宝藏博主
湖科大教书匠——计算机网络 “宝藏老师”、“干货满满”、“羡慕湖科大”…这些都是网友对这门网课的评价,可见网课质量之高! 湖南科技大学《计算机网络》微课堂是该校高军老师精心制作的视频课程,用简单的语言描述复杂的问题,…...
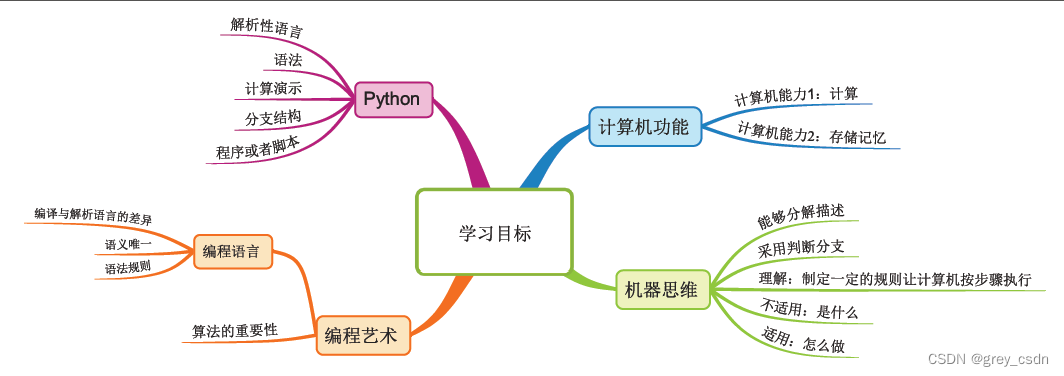
1694_week1_MIT使用Python编程学习手记1
全部学习汇总: GreyZhang/python_basic: My learning notes about python. (github.com) 首先说明一下,这部分信息的整理只是我个人的理解。由于自己的知识功底以及英语水准,很可能会有大量的疏漏。再此,我只想把自己学习时候的一…...
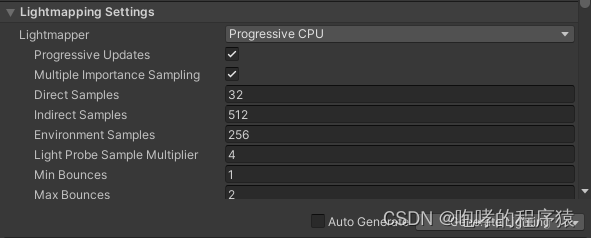
第二十一章 光源
光源是每个场景必不可少的部分,光源除了能够照亮场景之外,还可以产生阴影效果。 Unity中分为四种光源类型: 1. 方向光:Directional Light 用于模拟太阳光,方向光任何地方都能照射到。 2. 点光源:Point L…...
方向上接收论文总结)
CVPR 2023 超分辨率(super-resolution)方向上接收论文总结
目录 CVPR 2023图像超分任意尺度超分盲超分 视频超分特殊场景 总结参考资料 CVPR 2023 官网链接:https://cvpr2023.thecvf.com/ 会议时间:2023年6月18日-6月22日,加拿大温哥华 CVPR 2023统计数据: 提交:9155篇论文接…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
