【数据结构】二叉树(详细)
二叉树
- 1.树
- 1.1定义
- 1.2基本术语
- 1.3树形结构和线性结构
- 1.4树的存储结构
- 1.4.1双亲表示法
- 1.4.2孩子兄弟表示法
- 2.二叉树
- 2.1定义
- 2.2特殊二叉树
- 2.3性质
- 2.4存储结构
- 2.4.1顺序存储
- 2.4.2链式存储结构
- 3.二叉树的基本操作
- 3.1前序遍历(先序遍历)
- 3.2中序遍历
- 3.3后序遍历
- 3.4层序遍历
- 4.二叉树练习
- 5.二叉树的创建和销毁
- 5.1二叉树的创建
- 5.2二叉树的销毁
1.树
学习二叉树,首先得了解树,从树的基本概念出发。
1.1定义
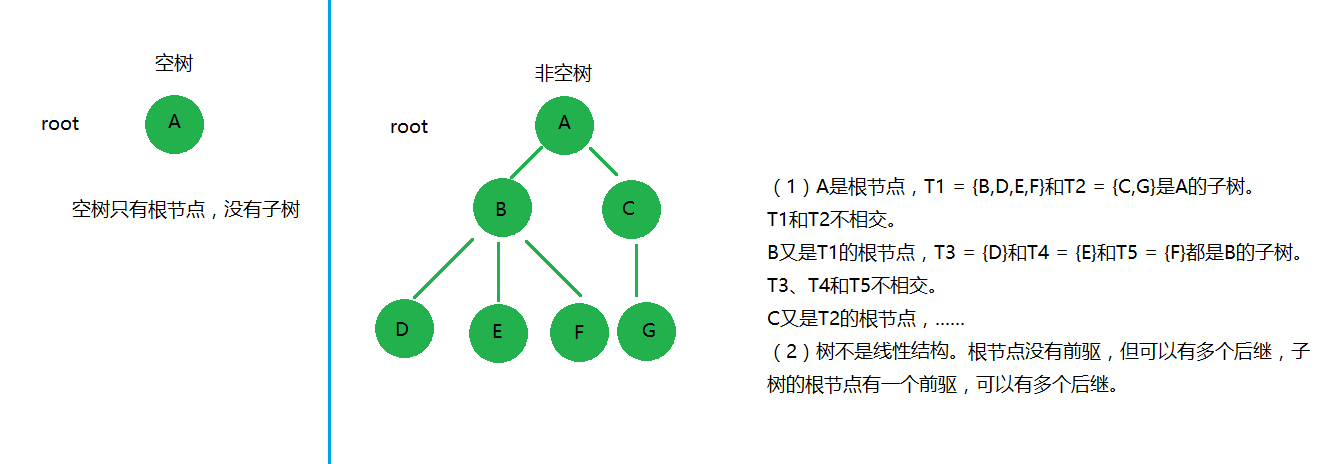
树是n个节点的的有限集合,是一种非线性结构。当n=0时称为空树,对于非空树T:(1)只有一个根结点(root);(2)除根节点外的其余结点可分为m个互不相交的有限集T1,T2,……,Tm,其中每个集合本身又是一棵树,称为根的子树。
1.2基本术语
- 结点:树的一个独立单元,包含一个数据元素或者指向其子树的分支。如图中的A,B,C等。
- 结点的度:结点拥有的子树数称为结点的度(也可以理解为这个结点有多少个孩子)。如A的度是2,B的度是3,D的度是0。
- 树的度:树的各个结点的度的最大值。如图中的树的度为3。
- 叶子结点(或者终端结点):度为0的结点。如图中的D,E,F,G。
- 非终端结点:度不为0的结点。除根结点外,非终端结点也称为内部结点。如图中B,C。
- 孩子结点(或者子节点):一个结点的子树的根结点称为该结点的孩子结点。如图中B和C是A的子结点。
- 双亲结点(或者父结点):一个结点有一个子结点,该结点称为其子结点的父结点。如图中,A是B和C的双亲结点。
- 兄弟结点:同一双亲的孩子之间互称兄弟。如图中B和C是兄弟结点。
- 祖先:从根结点到该结点所经分支上的所有结点。如D的祖先是A和B。
- 子孙:以某结点为根的子树的任一结点都称为该结点的子孙。如D,E,F是B的子孙。
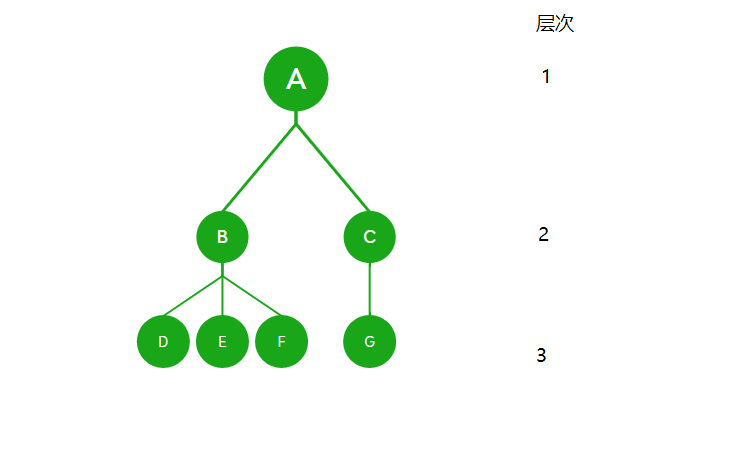
- 层次:从根结点开始,根结点为第一层,根的孩子为第二层,以此类推直到最后一层。如A是第一层,B是第二层,D是第三层。
- 深度:树中结点的最大层次。如A这棵树的深度是3。
- 森林:由m棵互不相交的树构成的集合。如去掉A结点,B和C这两棵子树就是森林。
这么多概念,但常用的只有结点的度、双亲结点、叶子结点、树的层次、树的高度、结点的祖先和子孙。
1.3树形结构和线性结构
| 树形结构 | 线性结构 |
|---|---|
| 树的根结点没有双亲结点 | 线性表的第一个元素没有前驱 |
| 树的叶子结点没有子结点 | 线性表的最后一个元素没有后继 |
| 树的内部结点有一个前驱和多个后继 | 线性表的其余元素只有一个前驱和一个后继 |
1.4树的存储结构
树有多种存储结构:双亲表示法、孩子链表表示法、孩子兄弟表示法等。由于今天的猪脚是二叉树,所以在这里简单介绍下双亲表示法和孩子兄弟表示法。
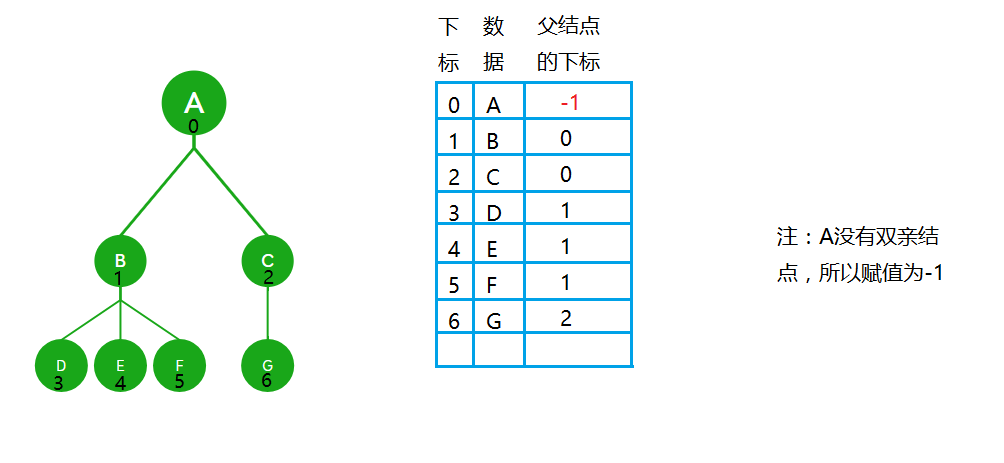
1.4.1双亲表示法
//结点
#define MAXSIZE 100
typedef int ElemType;
typedef struct
{ElemType x;//结点的数据int parent;//结点的双亲结点的下标
}PTNode;
typedef struct
{PTNode a[MAXSIZE];//结点数组int size;//结点个数
}PTree;
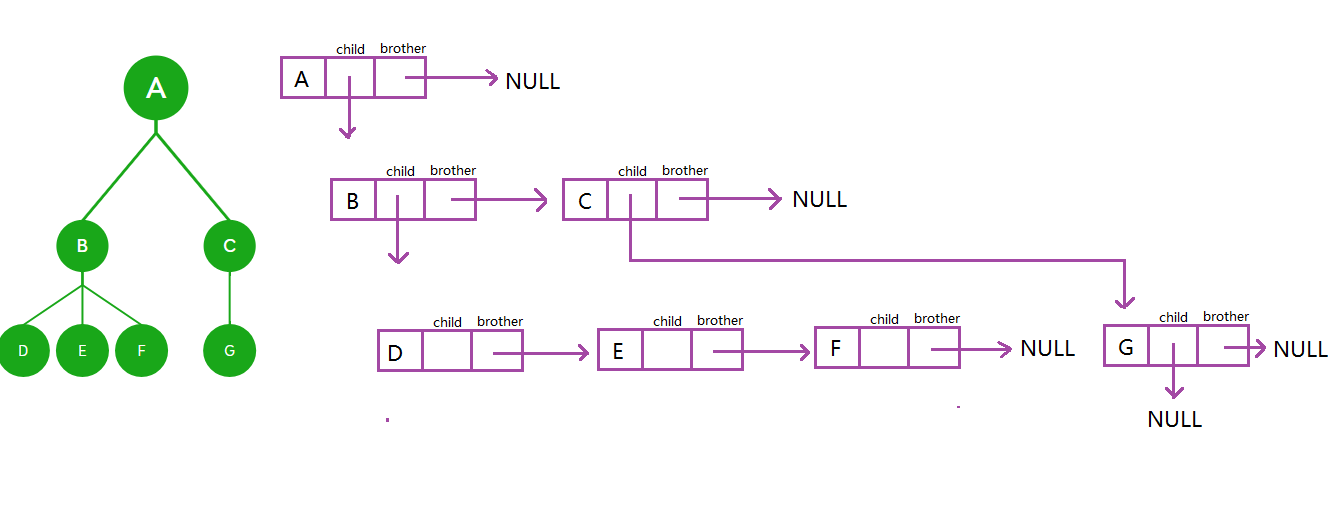
1.4.2孩子兄弟表示法
//结点
typedef int ElemType;
typedef struct CBTreeNode
{ElemType x;//数据struct CBTreeNode* firstchild;//指向结点的左孩子,也就是第一个孩子struct CBTreeNode* Nextbrother;//指向同一父结点的兄弟
}CBTNode;
2.二叉树
2.1定义
二叉树是n(n>=0)个结点的有限集合。当n=0时为空树,当n不为0时,二叉树有以下特点:1.每个结点的度不超过2(可以理解为二孩政策下的结点最多只能有两个孩子);
2.每个结点的左子树和右子树顺序不能颠倒,所以二叉树是有序树。
2.2特殊二叉树
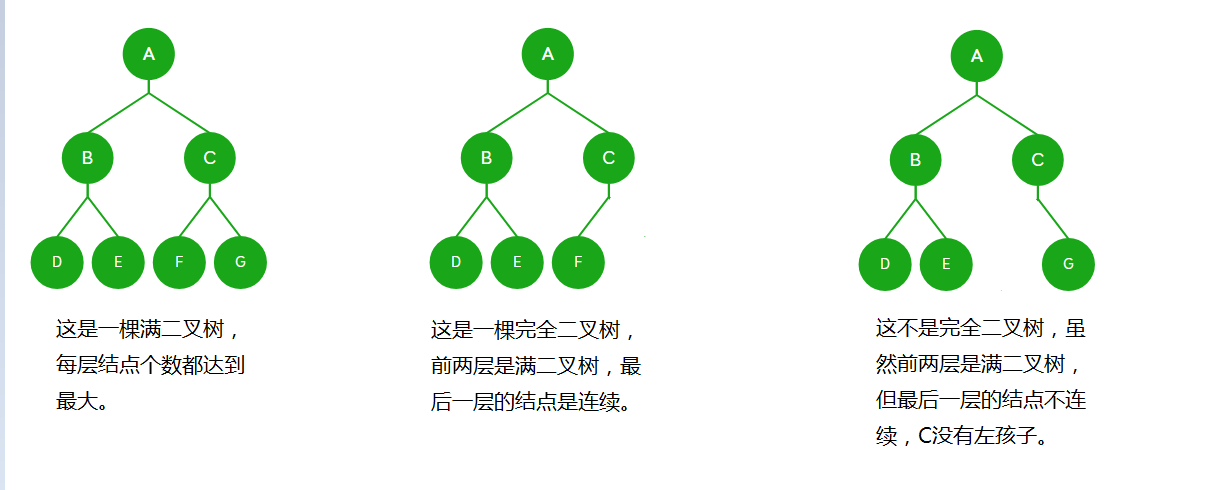
- 满二叉树:每一层结点数都达到最大,那么它就是满二叉树。如第1层最多有2 ^0个结点,第2层最多有 2 ^1个结点,则第k层最多有2 ^(k-1)个结点,假设这棵满二叉树有k层,那么它总共有2 ^0+2 ^1+……+2 ^(k-1) = 2 ^k-1个结点。
- 完全二叉树:深度为k,有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称为完全二叉树。(简介版:完全二叉树的前k-1层是满二叉树,最后一层从左到右依次连续)
2.3性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点。
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1。
- 对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
证明

- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log (n+1)(ps:log是以2
为底,n+1为对数)。
证明

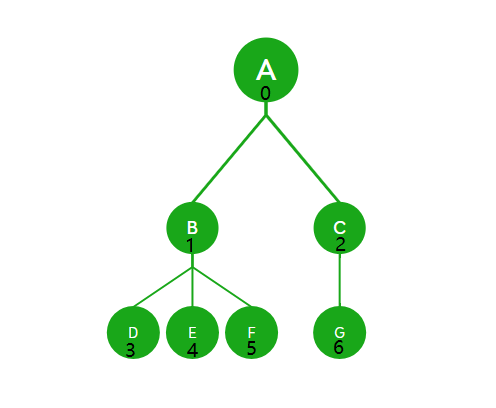
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
(1). 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
(2). 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
(3).若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2.4存储结构
2.4.1顺序存储
二叉树的顺序存储是用数组存储的,其中结点之间的关系用下标来表示。即二叉树的逻辑结构是树,但是其物理结构是数组。

但这种存储结构会造成空间浪费,适用于完全二叉树和满二叉树。

但这个结构却可以来实现一个很牛逼的排序:堆排序。
2.4.2链式存储结构
链式存储结构可以解决顺序存储结构浪费空间的问题,二叉树的链式存储表示有二叉链表、三叉链表、双亲链表、线索链表等。这里重点讲二叉链表。
//二叉树的节点
typedef int DataType;
typedef struct BinaryTreeNode
{DataType val;struct BinaryTreeNode* left;//指向左孩子的指针struct BinaryTreeNode* right;//指向右孩子的指针
}BTNode;
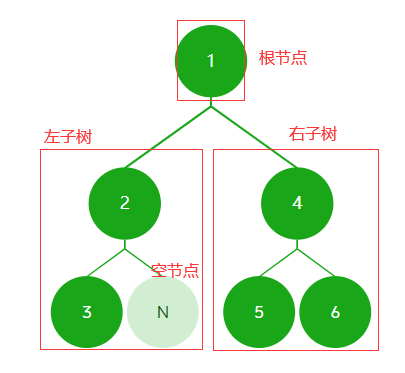
下面讲二叉树的基本操作。
3.二叉树的基本操作
遍历是指每个结点被访问一次且仅被访问一次。二叉树有一个前驱和两个后继,这注定其遍历不同于线性结构的遍历。二叉树的遍历有前序遍历、中序遍历,后序遍历,层序遍历。
3.1前序遍历(先序遍历)
- 概念
前序遍历:先访问根节点,再访问左子树和右子树。
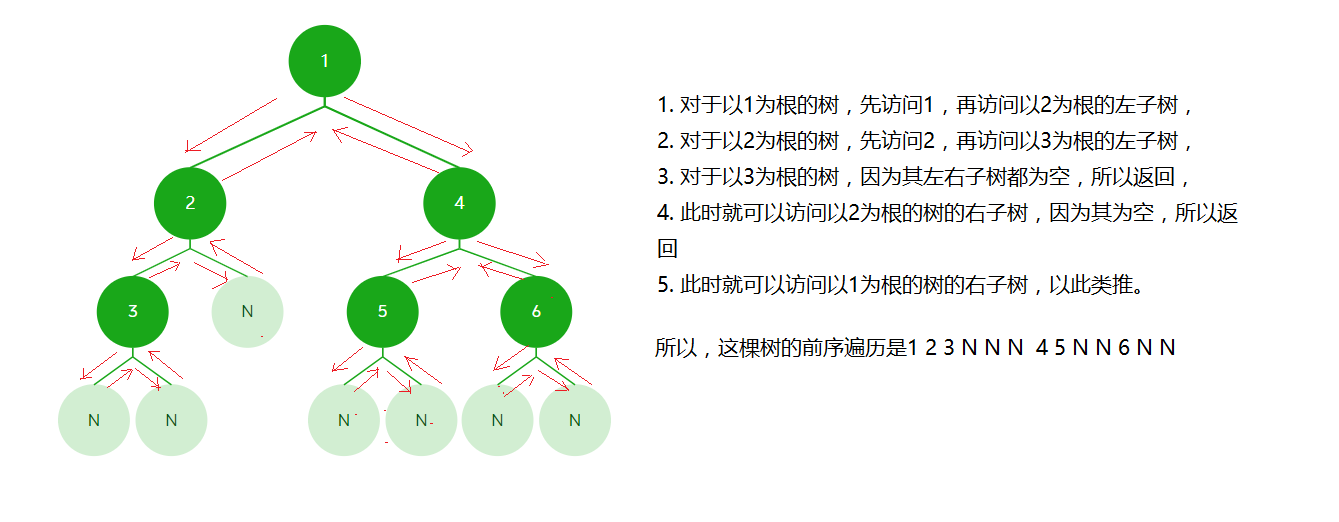
由图可知,树的前序遍历是递归的,所以可以用递归来实现。
- 代码实现
//先手动创建一个二叉树
BTNode* BuyNode(DataType x)//申请一个结点
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");return NULL;}newnode->left = newnode->right = NULL;newnode->val = x;return newnode;
}
BTNode* CreateBT()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;//返回根结点
}
//前序遍历
void PreOrder(BTNode* root)
{//思路:先访问根结点,再访问左子树和右子树if (root==NULL){printf("NULL ");return;}//先访问根结点printf("%d ", root->val);//再访问左右子树PreOrder(root->left);PreOrder(root->right);
}
int main()
{BTNode* root = CreateBT();PreOrder(root);return 0;
}
答案
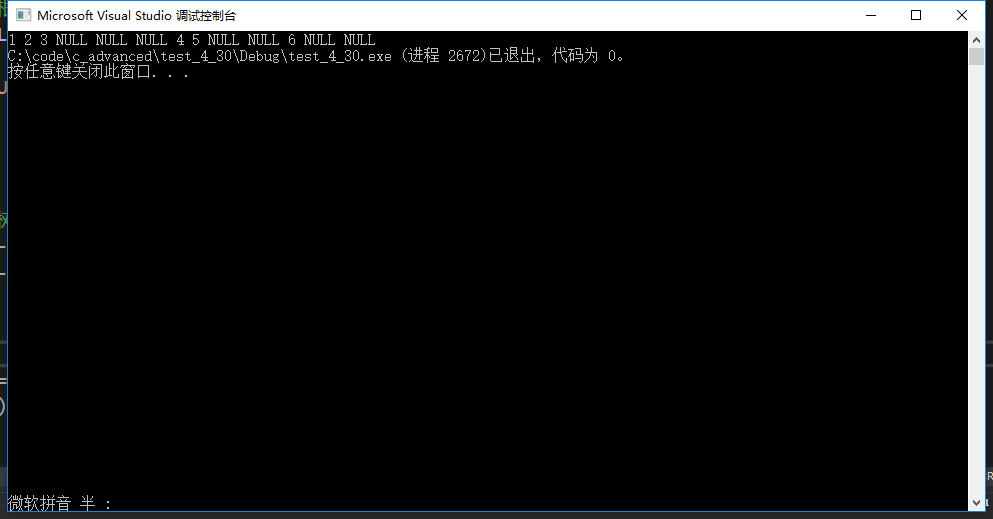
3.2中序遍历
- 概念
中序遍历:先访问左子树,再访问根节点,最后访问右子树。
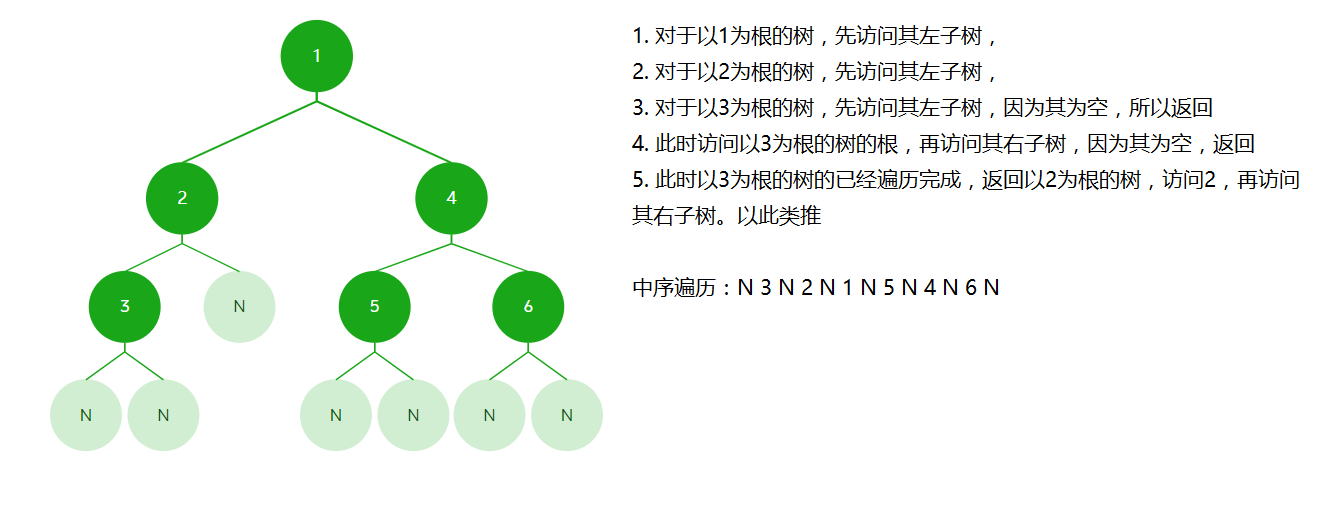
同样可以用递归实现 - 代码实现
// 二叉树中序遍历
void InOrder(BTNode* root)
{//思路:先访问左子树,再访问根节点,最后访问右子树if (root == NULL){printf("NULL ");return;}//先访问左子树InOrder(root->left);//再访问根节点printf("%d ", root->val);//最后访问右子树InOrder(root->right);
}
答案
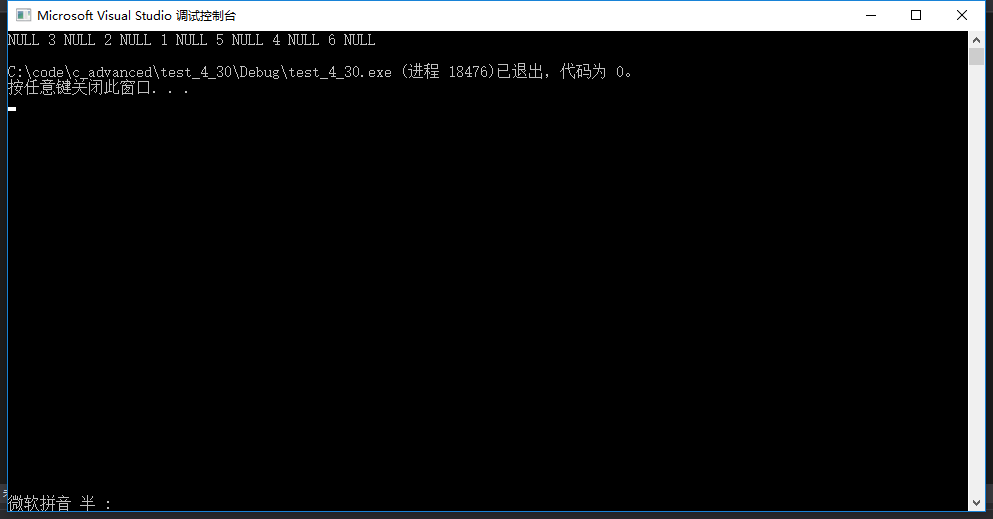
3.3后序遍历
- 概念
后序遍历:先访问左子树,再访问右子树,最后访问根节点。
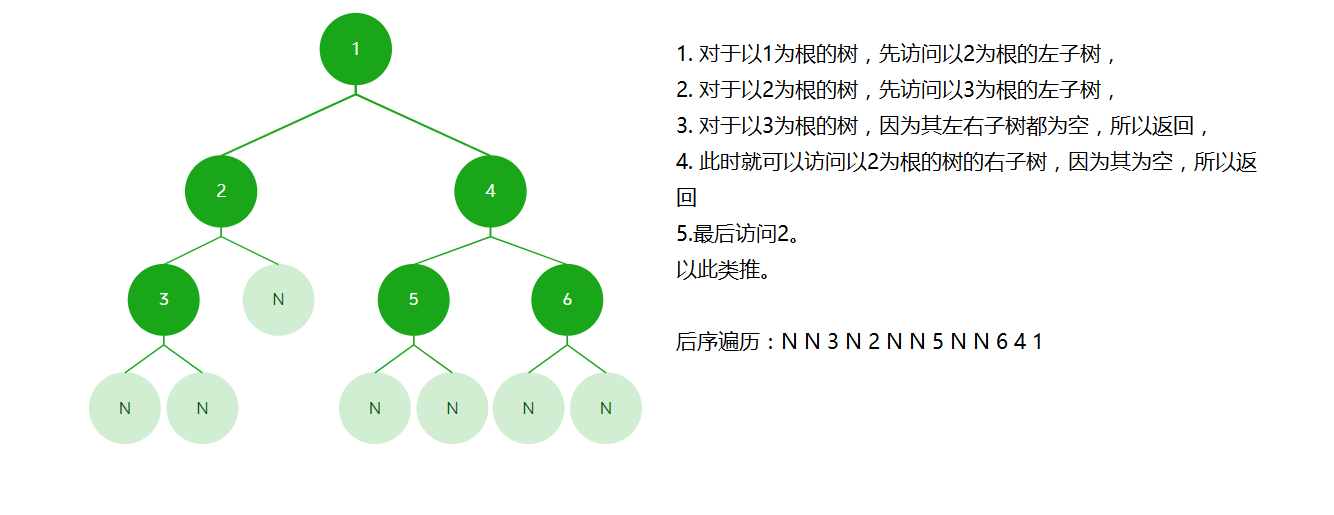
- 代码实现
//后序遍历
void PostOrder(BTNode* root)
{//思路:先访问左子树,再访问右子树,最后访问根结点if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
答案
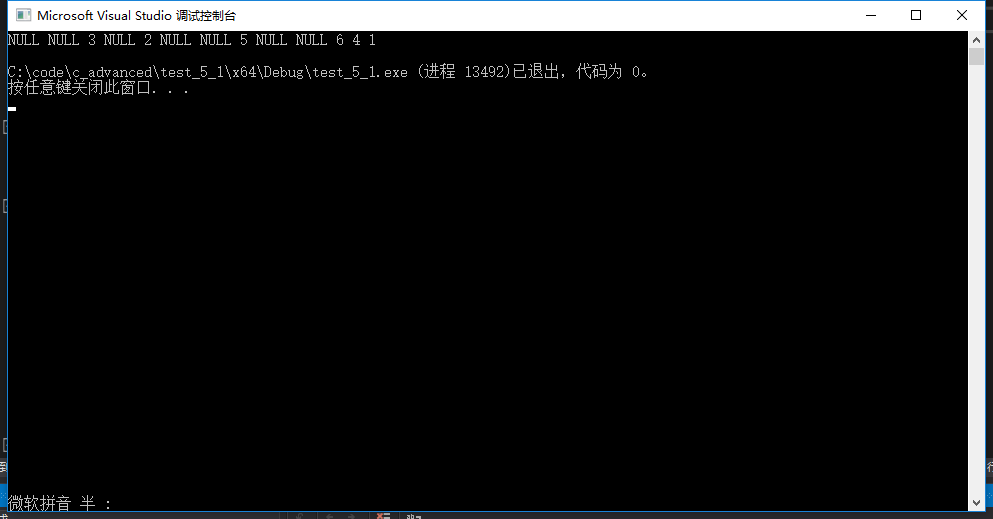
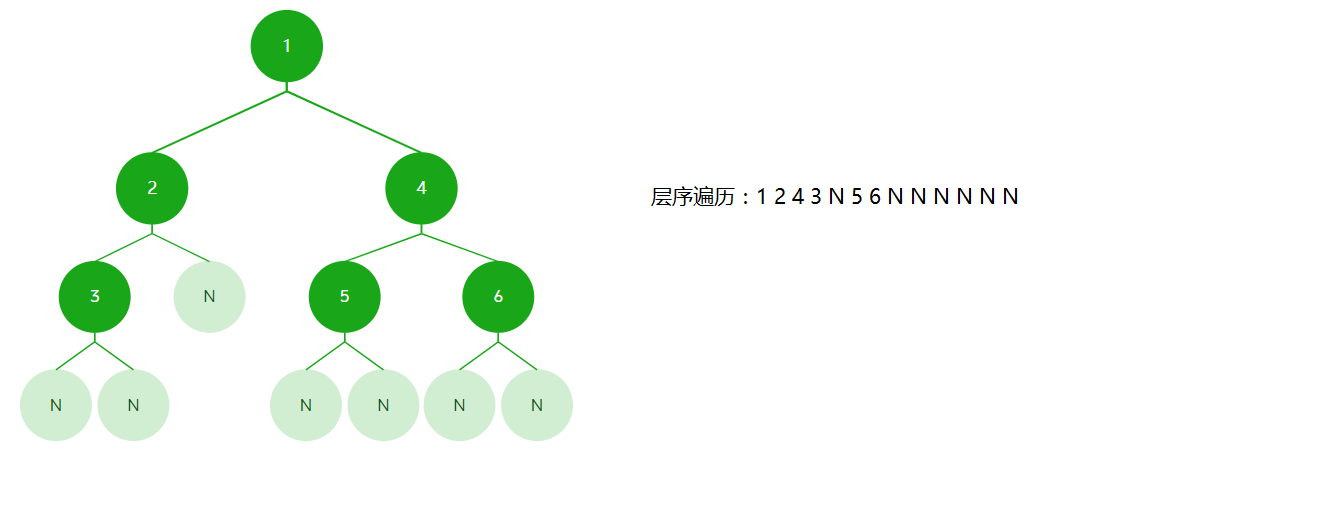
3.4层序遍历
- 概念
层序遍历:从上到下,从左到右,依次访问。
- 代码实现
// 层序遍历
void LevelOrder(BTNode* root)
{//思路:用队列实现,出队一层,入队下一层Queue q;QInit(&q);//如果非空就直接入队if (root){QPush(&q, root);}//队列中只入队非空元素while (!QEmpty(&q)){//先出队BTNode* tmp = QPop(&q);printf("%d ", tmp->val );//再判断左右子树是否为空if (tmp->left){QPush(&q, tmp->left);}if (tmp->right){QPush(&q, tmp->right);}}QDestroy(&q);
}
答案
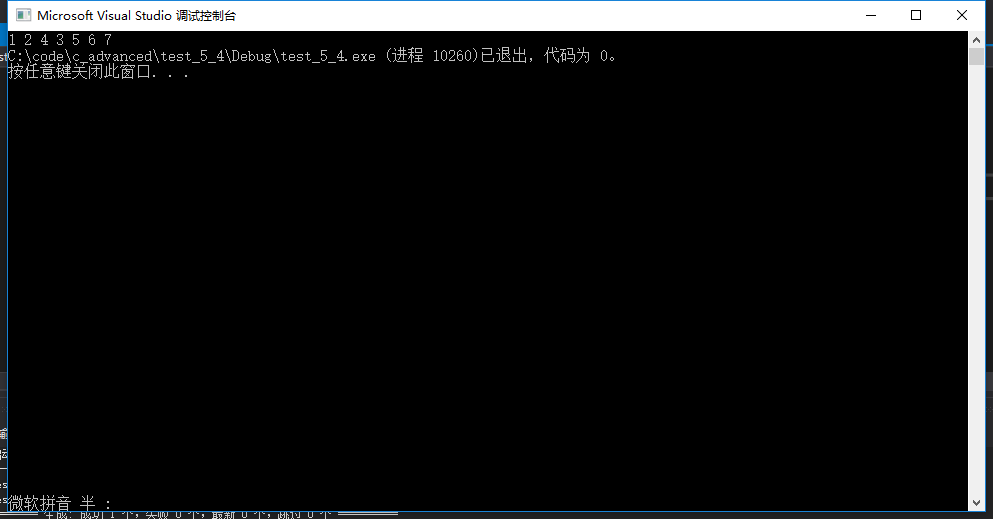
4.二叉树练习
样例
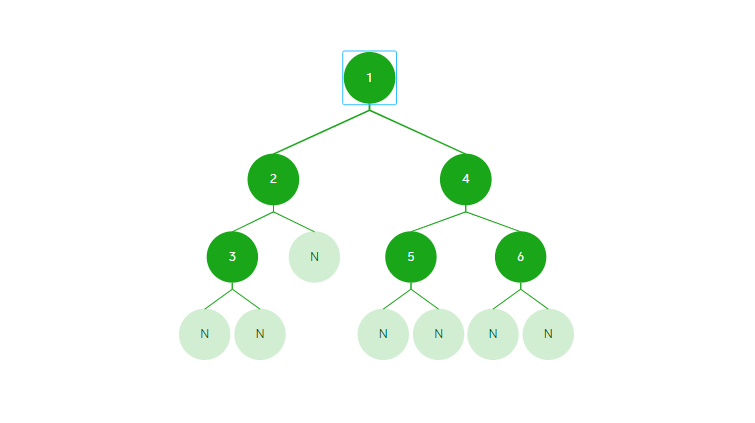
- 求二叉树的节点个数
// 二叉树节点个数//法一:
int size = 0;//也可以使用静态变量
void TreeSize(BTNode* root)
{//思路:只要节点不为空,就记录一次if (root == NULL){return 0;}++size;TreeSize(root->left);TreeSize(root->right);
}//法二:
int BinaryTreeSize(BTNode* root)
{//思路:二叉树的节点个数 = 左子树的节点个数 + 右子树的节点个数if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1 ;
}
注意
但是法一有个弊端:size是全局(或静态)变量,每次调用都得初始化一次。
答案
- 求二叉树的叶子节点个数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{//思路:二叉树的叶子节点 = 左子树的叶子节点 + 右子树的叶子节点if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
答案
- 求二叉树的高度
// 二叉树的高度(深度)
int TreeHeight(BTNode* root)
{// 思路:二叉树的高度 = 左子树的高度和右子树的高度的最大值 + 1if (root == NULL){return 0;}int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;
}
答案
- 求第k层节点个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{//思路://对于第一层,是求第k层节点个数(k)//对于第二层,是求第k-1层节点个数(k-1)//……//对于第k层,是求这一层节点个数(1)//第k层节点个数 = 左子树第k层节点个数 + 右子树第k层节点个数if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
答案
- 判断是否是单值二叉树(LeetCode965)OJ链接
单值二叉树:二叉树的每个节点都有相同的值
// 判断是否是单值二叉树
bool isUnivalTree(BTNode* root)
{//思路:比较根节点与左右子树是否相等,不相等就返回false,相等就判断左右子树是否是单值二叉树if (root == NULL){return true;}if (root->left && root->left->val != root->val){return false;}if (root->right && root->right->val != root->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}
答案
- 查找一个值为x的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, DataType x)
{//思路:先判断根的值是否与x相等,相等就返回根,//不等就判断是否与左子树相等,相等就返回//不等就判断是否与右子树相等,相等就返回,不等就返回NULLif (root == NULL){return NULL;}if (root->val == x){return root;}BTNode*tmp = BinaryTreeFind(root->left, x);if (tmp != NULL){return tmp;}tmp = BinaryTreeFind(root->right, x);if (tmp != NULL){return tmp;}return NULL;
}
- 判断两棵二叉树是否相等(LeetCode100)OJ链接
// 判断两棵二叉树是否相等
bool isSameTree(BTNode* p, BTNode* q)
{//思路:先判断根结点是否相等,再判断左子树是否相等,最后判断右子树是否相等if (p == NULL && q == NULL){return true;}if (p == NULL || q == NULL){return false;}if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
答案
- 判断是否是对称二叉树(LeetCode101)OJ链接
bool isLefRig(BTNode* p1, BTNode* p2)//功能类似于判断两棵二叉树是否相等
{if (p1 == NULL && p2 == NULL){return true;}if (p1 == NULL || p2 == NULL){return false;}if (p1->val != p2->val){return false;}return isLefRig(p1->left, p2->right) && isLefRig(p1->right, p2->left);
}
bool isSymmetric(BTNode* root)
{
· //思路:写一个辅助函数,功能与判断二叉树是否相等类似if (root == NULL){return true;}return isLefRig(root->left, root->right);
}
答案
- 二叉树的前序遍历(LeetCode144)OJ链接
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void PreOrder(struct TreeNode* root, int* a, int* i)
{if (root == NULL){return;}//先对根结点进行操作,再对左右子树进行操作a[(*i)++] = root->val;PreOrder(root->left, a, i);PreOrder(root->right, a, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){//我们需要知道这棵树的大小,再来动态申请int size = TreeSize(root);*returnSize = size;int* ret = (int*)malloc(sizeof(int) * size);//写一个函数来实现遍历,不要在这个函数遍历,因为遍历需要递归,所以TreeSize会重复调用int i = 0;//用来记录数组的下标,方便存储数据PreOrder(root, ret, &i);//为什么要传下标的地址?因为要对下标进行修改return ret;
}
答案
- 二叉树的中序遍历(LeetCode94)OJ链接
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void InOrder(struct TreeNode* root, int* a, int* i)
{if (root == NULL){return;}InOrder(root->left, a, i);a[(*i)++] = root->val;InOrder(root->right, a, i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){//我们需要知道这棵树的大小,再来动态申请int size = TreeSize(root);*returnSize = size;int* ret = (int*)malloc(sizeof(int) * size);//写一个函数来实现遍历,不要在这个函数遍历,因为遍历需要递归,所以TreeSize会重复调用int i = 0;//用来记录数组的下标,方便存储数据InOrder(root, ret, &i);//为什么要传下标的地址?因为要对下标进行修改return ret;
}
结果
- 二叉树的后序遍历(LeetCode145)OJ链接
int BinaryTreeSize(struct TreeNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
void PostOrder(struct TreeNode* root, int* ret, int* pi)
{if (root == NULL){return 0;}PostOrder(root->left, ret, pi);PostOrder(root->right, ret, pi);ret[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){int size = BinaryTreeSize(root);*returnSize = size;int* ret = (int*)malloc(sizeof(int) * size);//用来存放前序序列int i = 0;PostOrder(root, ret, &i);return ret;
}
结果
- 判断一棵树是否是另一棵树的子树
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{//思路:用当前节点所在树与sub进行比较,相等返回真,不相等用当前根结点的左子树比较,再不相等用右子树比较if (root == NULL){return false;}if (isSameTree(root, subRoot)){return true;}return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
结果
- 判断是否是完全二叉树
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{//思路:利用层序遍历,将完全二叉树的所有节点全部入队,//当出队时节点为NULL,如果为完全二叉树,则队列中的其余节点都是NULL,//所以最后判断队列中的节点是否不为NULL,即可判断Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode*tmp = QueueFront(&q);QueuePop(&q);if (tmp == NULL){break;//当遇到NULL,就跳出循环}else{QueuePush(&q, tmp->left);//如果为NULL也入队QueuePush(&q, tmp->right);}}while (!QueueEmpty(&q)){BTNode* tmp = QueueFront(&q);QueuePop(&q);if (tmp){QueueDestroy(&q);//注意销毁队列,防止内存泄漏return false;}}QueueDestroy(&q);//等下学习怎么销毁,先记住它有销毁的功能return true;
}
int main()
{char arr[100] = { 0 };scanf("%s", arr);int i = 0;int size = strlen(arr);BTNode* root = CreateBT(arr, &i,size);InOrder(root);
}
5.二叉树的创建和销毁
前面的二叉树是我们手动创建的,现在学习了前序、中序、后序遍历,就可以利用它们来创建和销毁二叉树。
5.1二叉树的创建
二叉树遍历OJ链接
BTNode* BuyNode(DataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");return NULL;}newnode->left = NULL;newnode->right = NULL;newnode->val = x;return newnode;
}
BTNode* CreateBT(char* arr, int* pi,int size)
{ //ABC##DE#G##F###if (*pi == size)//递归的停止条件{return NULL;}if (arr[*pi] == '#'){(*pi)++;//遇到#,不要忘记跳过return NULL;}BTNode* root = BuyNode(arr[(*pi)++]);root->left = CreateBT(arr, pi,size);root->right = CreateBT(arr, pi,size);return root;
}
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%c ", root->val);InOrder(root->right);
}
int main()
{char arr[100] = { 0 };scanf("%s", arr);int i = 0;int size = strlen(arr);BTNode* root = CreateBT(arr, &i,size);InOrder(root);
}
结果
5.2二叉树的销毁
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{//如果用前序或者中序遍历销毁二叉树会导致内存泄漏(找不到左右子树)//所以用后序遍历销毁二叉树if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root == NULL;
}
相关文章:

【数据结构】二叉树(详细)
二叉树 1.树1.1定义1.2基本术语1.3树形结构和线性结构1.4树的存储结构1.4.1双亲表示法1.4.2孩子兄弟表示法 2.二叉树2.1定义2.2特殊二叉树2.3性质2.4存储结构2.4.1顺序存储2.4.2链式存储结构 3.二叉树的基本操作3.1前序遍历(先序遍历)3.2中序遍历3.3后序…...

蓝牙耳机哪款性价比高一些?2023年性价比最高的蓝牙耳机推荐
随着科技的进步,蓝牙耳机已然成为我们生活中的一部分,无论是通勤、追剧、运动或者玩游戏,大都会用到蓝牙耳机。那么,哪款蓝牙耳机的性价比高一些?相信大多数人在选择产品的时候,都会看性价比。接下来&#…...

等保2.0存在的问题
等保制度和技术要求 国家信息安全等级保护制度(二级)相关要求包含技术要求和管理要求,技术要求包含:物理安全、网络安全、主机安全、应用安全及数据安全及备份恢复;管理要求包含:安全管理机构、安全管理制度、人员安全管理、系统建设管理、系统运维管理。 一、 技术要求 …...
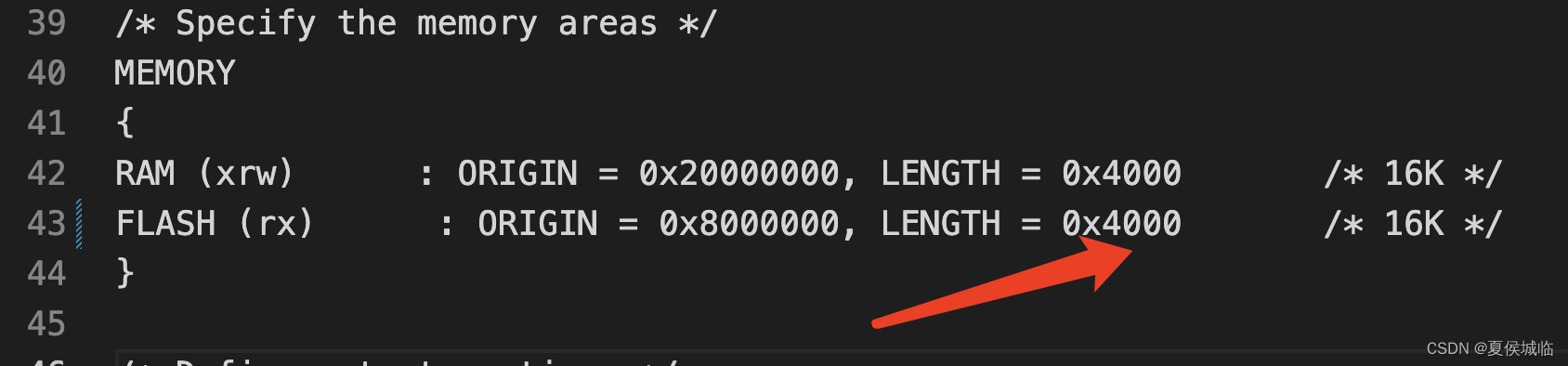
国民技术N32G430开发笔记(9)- IAP升级 Bootloader的制作
IAP升级 Bootloader的制作 1、上节提到Flash的分区,0x8000000-0x8004000为Boot分区,我们的bootloader就烧录到此分区。 Bootloader很简单,新建一个普通的工程, 也不用初始化外部设备,开机后,直接跳转到 A…...
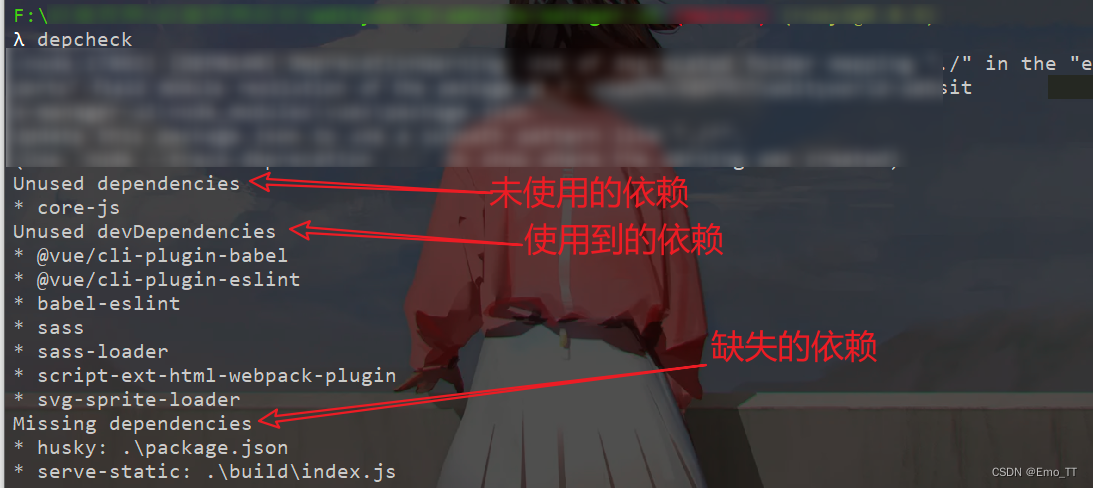
如何使用depcheck检查vue和react的依赖,以后不用把时间浪费在依赖问题上了
当我们在开发 JavaScript 项目时,会引入各种依赖库。但是有些依赖库可能只用到了部分功能,或者已经不再需要了,但是却一直被保留在项目中。 这些未使用的依赖库会占据项目的空间,增加项目的复杂度,影响项目的性能。为…...
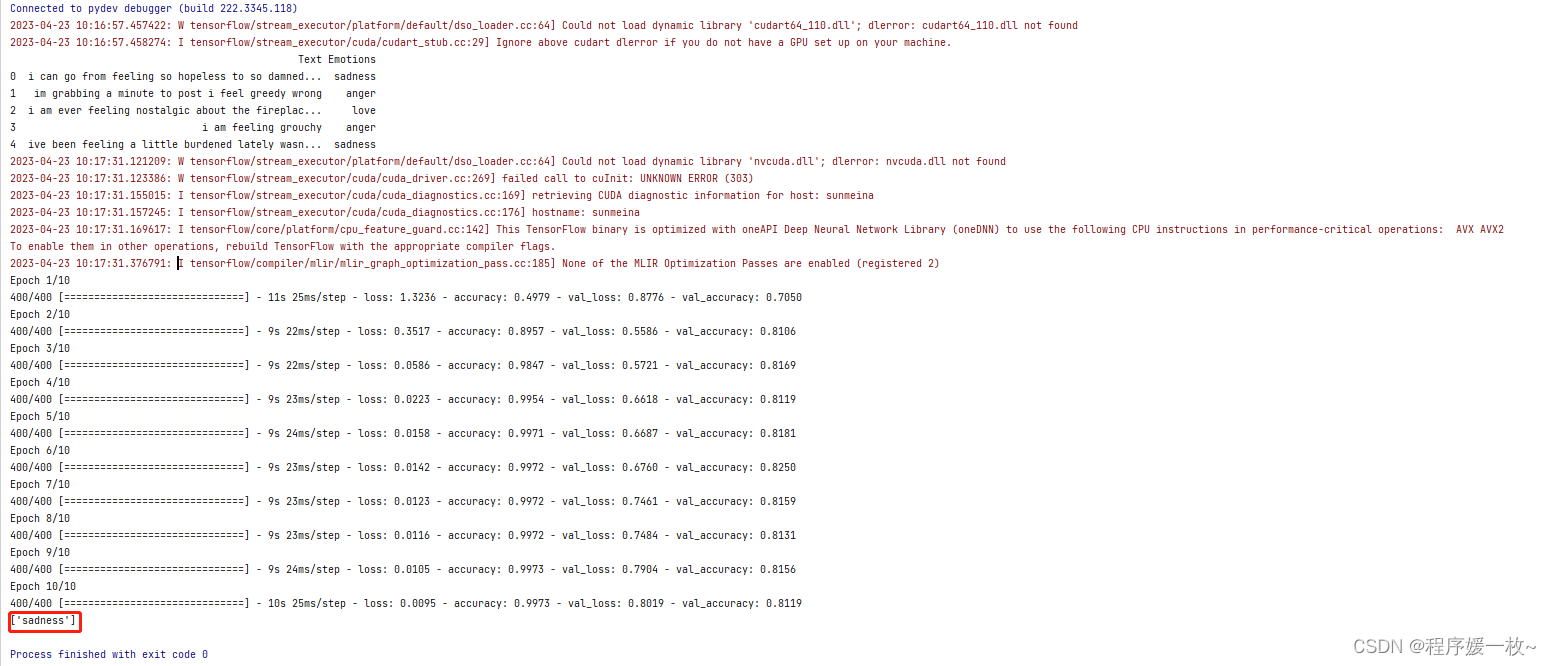
使用Python和机器学习进行文本情感分类
使用Python和机器学习进行文本情感分类 1. 效果图2. 原理3. 源码参考这篇博客将介绍如何使用Python进行机器学习的文本情感分类(Text Emotions Classification)。 1. 效果图 训练文本及情感分类前5条数据如下: 训练过程及测试文本情感分类效果图如下: 可以看到 对文本“S…...

QML路径视图(The PathView)
路径视图(PathView)非常强大,但也非常复杂,这个视图由QtQuick提供。它创建了一个可以让子项沿着任意路径移动的视图。沿着相同的路径,使用缩放(scale),透明(opacity&…...
5月4号软件资讯更新合集.....
🚀 Layui 2.8.2 发布 更新日志 table 修复 autoSort: true 时,更改 table.cache 未同步到 data 属性的问题 修复 多级表头存在 hide 表头属性时,执行完整重载可能出现的错位问题 修复 未开启 page 属性时底边框缺失问题 优化 打印内容中…...

基于 Rainbond 的混合云管理解决方案
内容概要:文章探讨了混合云场景中的难点、要点,以及Rainbond平台在跨云平台的混合云管理方面的解决方案。包括通过通过统一控制台对多集群中的容器进行编排和管理,实现了对混合云中应用的一致性管理。文章还介绍了Rainbond平台在混合云环境下…...
加强网络风险生命周期
当今业务环境中云原生应用程序的激增帮助组织简化了运营。 企业现在可以近乎实时地监控数据、与客户互动并分享见解,帮助他们克服曾经阻碍生产力的低效率问题。 然而,使用云也极大地扩展了企业可利用的攻击面。 CSPM、CWPP、CNAPP、SAST、SCA、IaC、D…...
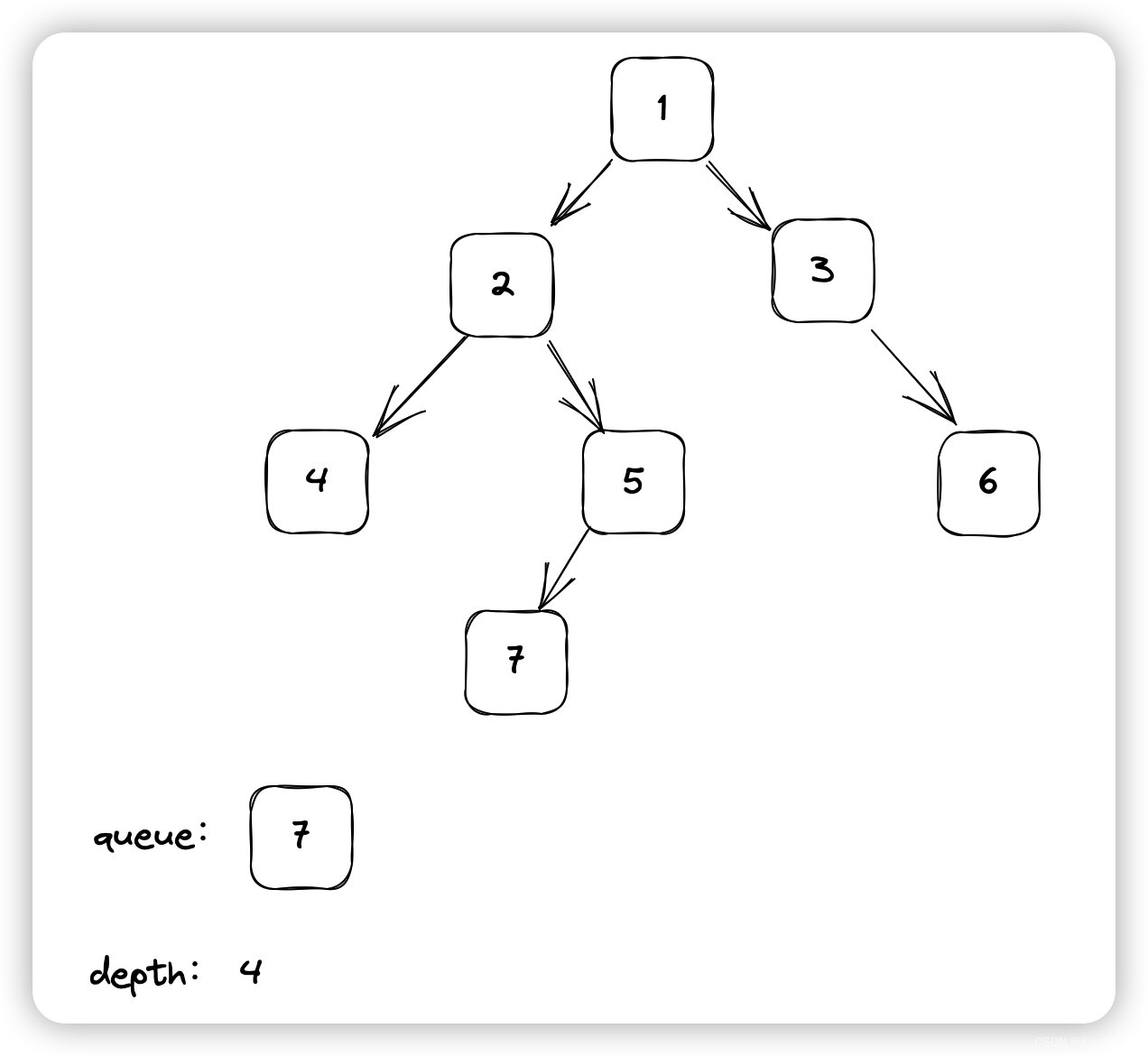
Java——二叉树的深度
题目链接 牛客网在线oj题——二叉树的深度 题目描述 输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度,根节点的深度视为 1 。 数据范围&am…...
)
一般现在时(二)
一般现在时(二) 1.什么叫实义动词? 实义动词是指表示有具体意思的动词,也叫行为动词。 例如:like(喜欢) eat(吃) live(居住) have(有) run(跑)等等。 实义动词占英语中动词的绝大多数 🔖我们已学过的be动词可译为是,有时译为成为,有时则没有具体意…...

leetcode657. 机器人能否返回原点
题目描述解题思路执行结果 leetcode657. 机器人能否返回原点 题目描述 机器人能否返回原点 在二维平面上,有一个机器人从原点 (0, 0) 开始。给出它的移动顺序,判断这个机器人在完成移动后是否在 (0, 0) 处结束。 移动顺序由字符串 moves 表示。字符 mov…...

DAY 48 Nginx的 location与rewrite模块
[正则表达式] 常用的[Nginx] 正则表达式 $ :匹配输入字符串的结束位置* :匹配前面的字符零次或多次。如“ol*”能匹配“o”及“ol”、“oll” :匹配前面的字符一次或多次。如“ol”能匹配“ol”及“oll”、“olll”,但不能匹配“…...

Linux 常用操作技巧
Linux 操作技巧大全 Linux是一种强大的操作系统,掌握各种操作技巧可以帮助我们惬意地使用它。在这篇博客中,我们将分享一些实用的Linux技巧,希望能对您有所帮助! 1. 使用Tab进行自动补全 在输入命令时,按下Tab键可…...
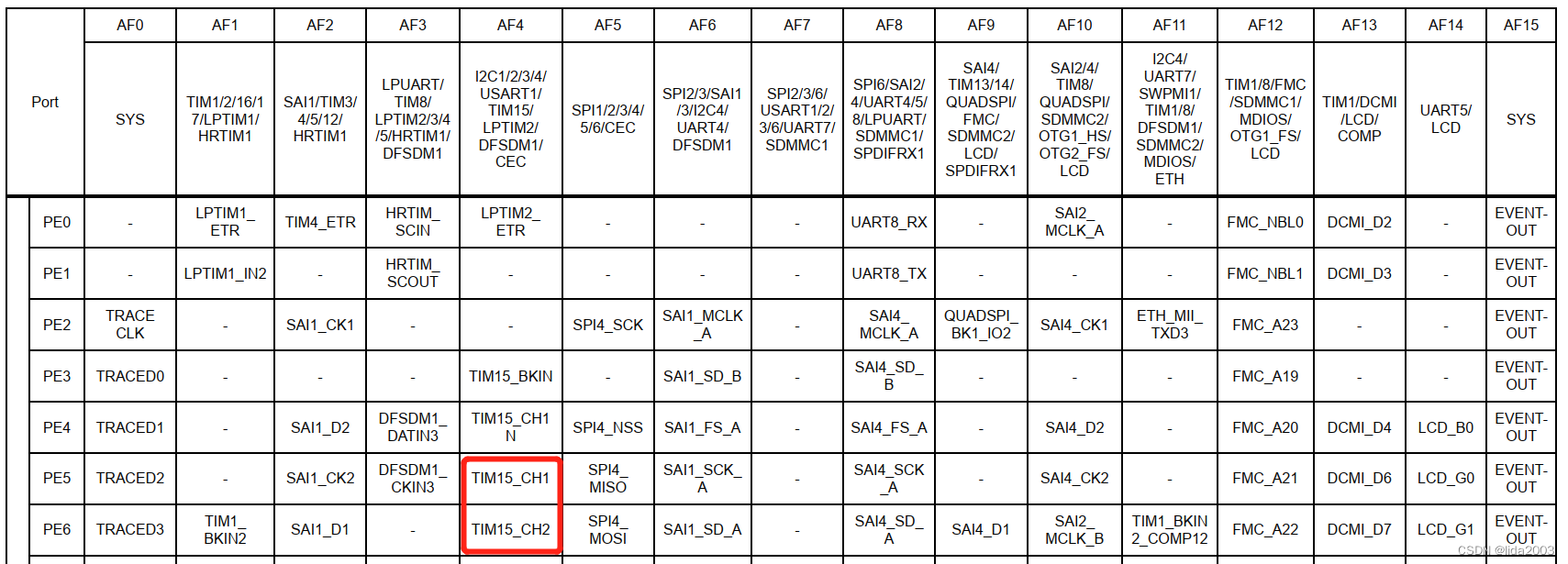
BetaFlight统一硬件配置文件研读之timer命令
BetaFlight统一硬件配置文件研读之timer命令 1. 源由2. 代码分析3. 实例分析4. 配置情况4.1 AFn配置查表4.2 timer4.3 timer show4.4 timer pin list 5. 参考资料 统一硬件配置文件的设计是一种非常好的设计模式,可以将硬件和软件的工作进行解耦。 1. 源由 cli命令…...
码出高效:Java开发手册笔记(java对象四种引用关系及ThreadLocal)
码出高效:Java开发手册笔记(java对象四种引用关系及ThreadLocal) 前言一、引用类型二、ThreadLocal价值三、ThreadLocal副作用 前言 “水能载舟,亦能覆舟。”用这句话来形容 ThreadLocal 最贴切不过。ThreadLocal 初衷是在线程并…...
为什么要进行数据决策?数据决策对企业而言有何重要意义?
“大数据”几乎已成为时下最时髦的词汇,不夸张地说,当今各行各业无不对大数据充满了向往,希望自己在新一轮的大数据营销中抢占先机。同时,从大数据中引申出的数据挖掘、数据分析、数据安全等数据运用技术也成为人们热捧的焦点。 …...

2. Java 异常体系
2.1 Throwable java.lang.Throwable 类是 Java 程序执行过程中发生的异常事件对应的类的根父类。 Throwable 中的常用方法: public void printStackTrace():打印异常的详细信息。 包含了异常的类型、异常的原因、异常出现的位置、在开发和调试阶段都得…...

如何学好STM32,需要哪些步骤?
学习STM32应用于项目开发需要以下步骤: 学习STM32的基本知识:包括STM32的架构、寄存器、外设等,理解STM32的工作原理和基本操作方法。 学习嵌入式系统和RTOS的基础知识:了解嵌入式系统的概念、RTOS的基本原理和使用方法ÿ…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
