Java——二叉树的深度
题目链接
牛客网在线oj题——二叉树的深度
题目描述
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度,根节点的深度视为 1 。
数据范围:节点的数量满足 0≤n≤100 ,节点上的值满足0≤val≤100
进阶:空间复杂度 O(1) ,时间复杂度 O(n)
假如输入的用例为{1,2,3,4,5,#,6,#,#,7},那么如下图:
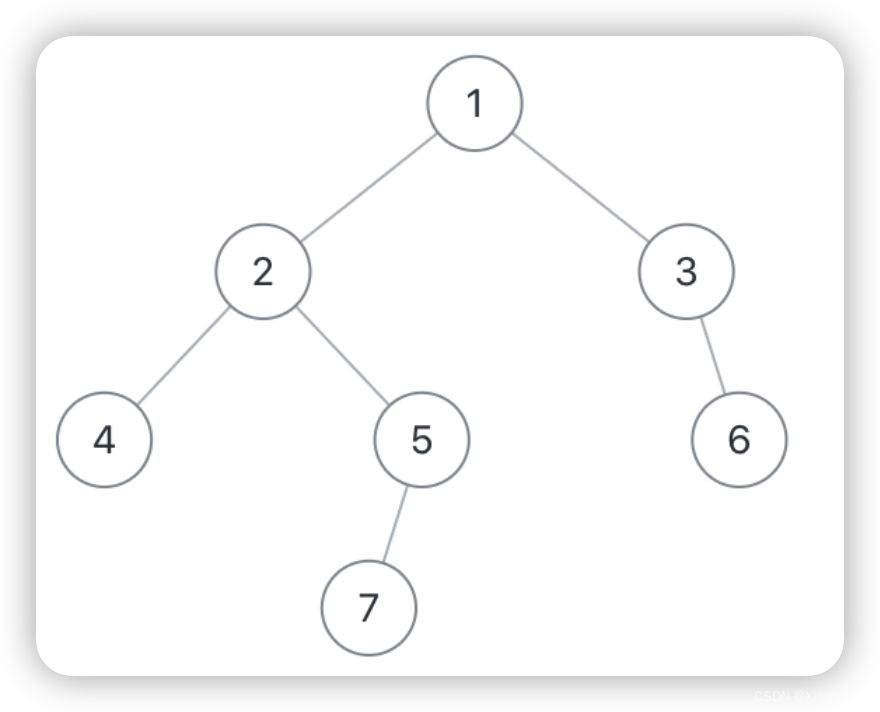
题目示例
示例1
输入:
{1,2,3,4,5,#,6,#,#,7}
返回值:
4
示例2
输入:
{}
返回值:
0
解题思路一
使用广度优先搜索,将二叉树进行层序遍历,每遍历一层就将depth++
广度优先遍历需要借助队列,首先将根节点加入到queue中,然后每次先确定队列的大小size,然后弹出size个元素,分别将这些元素的左子树和右子树加入到队列中(如果不为null)
上面每次弹出size个元素的过程就是遍历一层的过程,因此此时将depth++即可
例如:
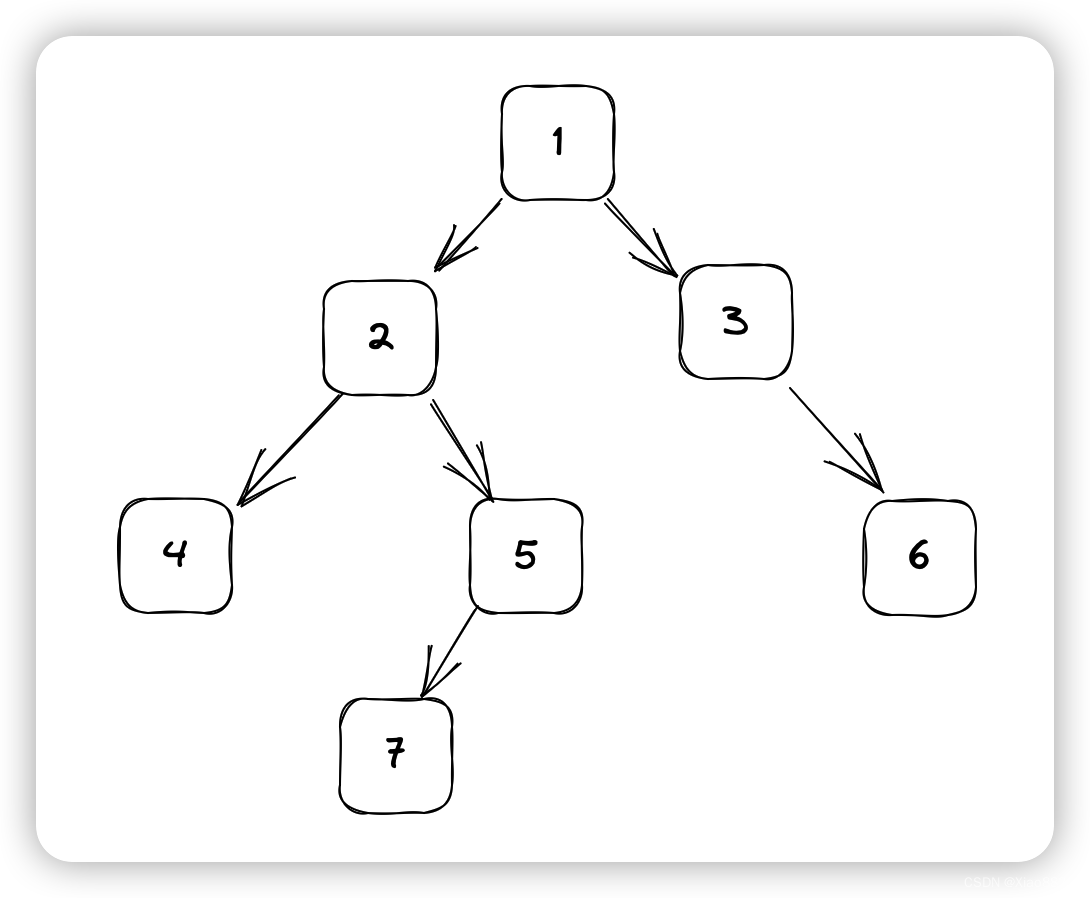
首先将根节点加入队列中,depth++
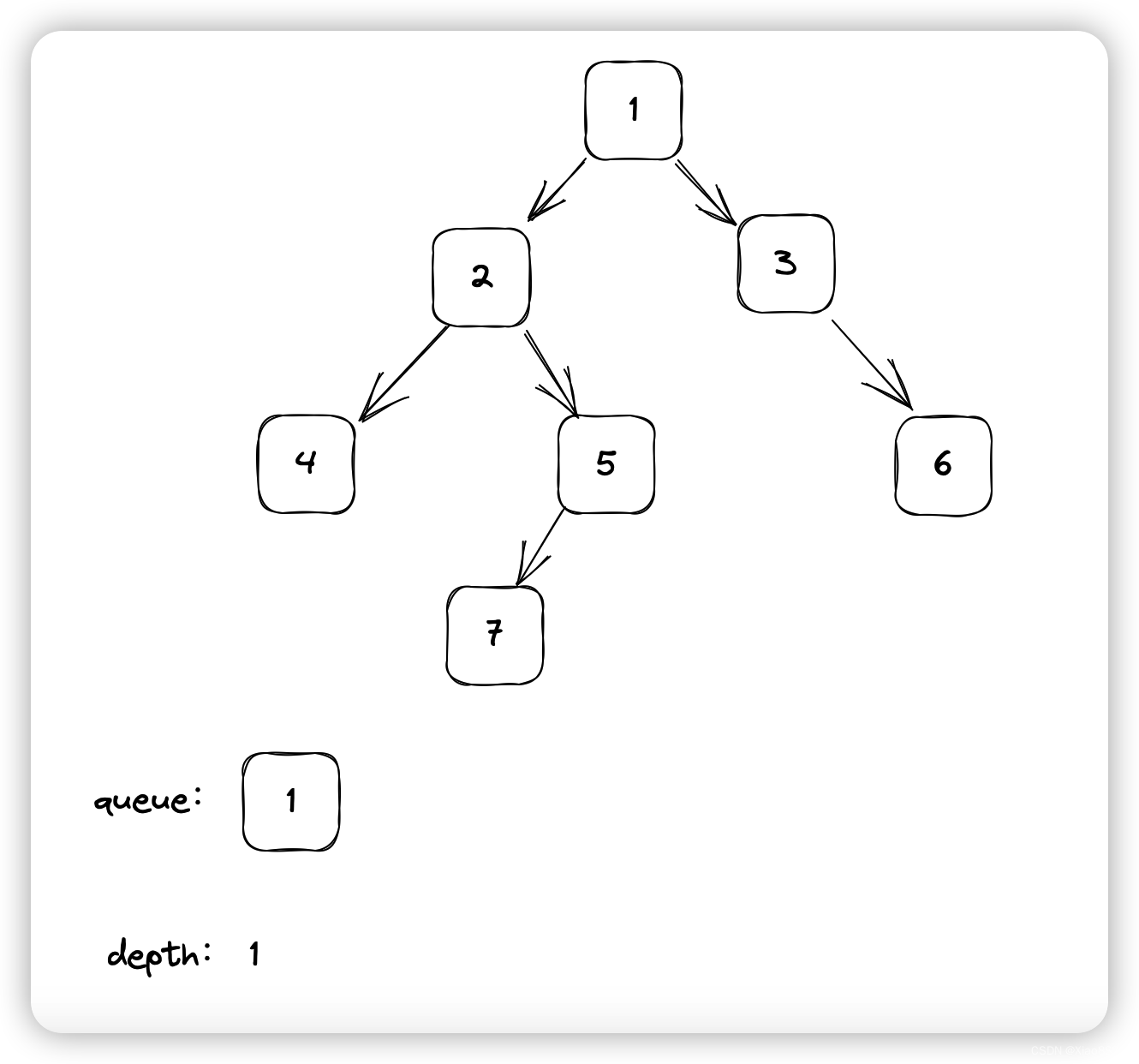
现在queue的长度是1,弹出1个元素,将其左子树和右子树添加进队列,depth++

现在queue的长度是2,弹出2个元素,将其左子树和右子树添加进队列,depth++
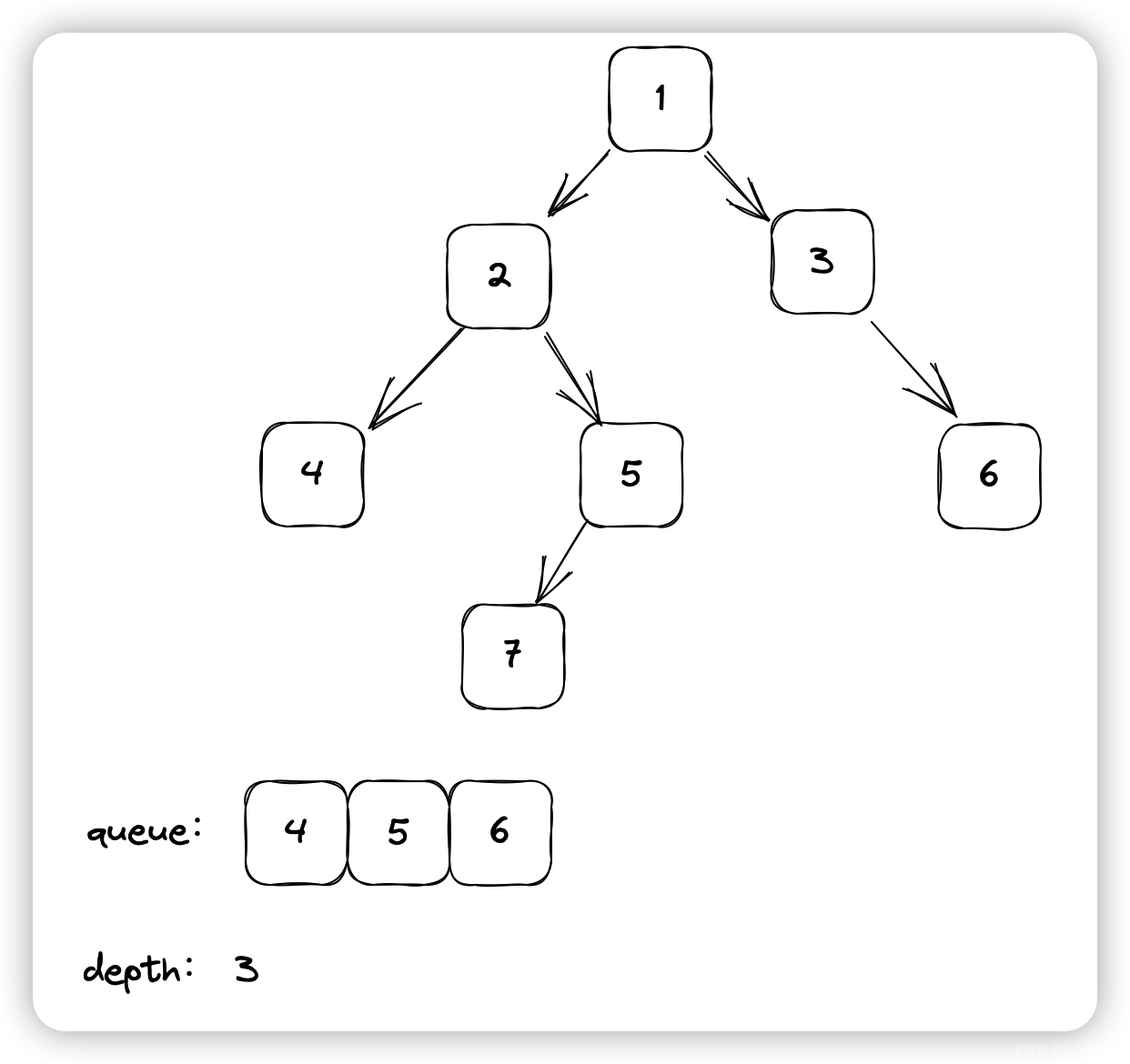
现在queue的长度是3,弹出3个元素,将其左子树和右子树添加进队列,depth++
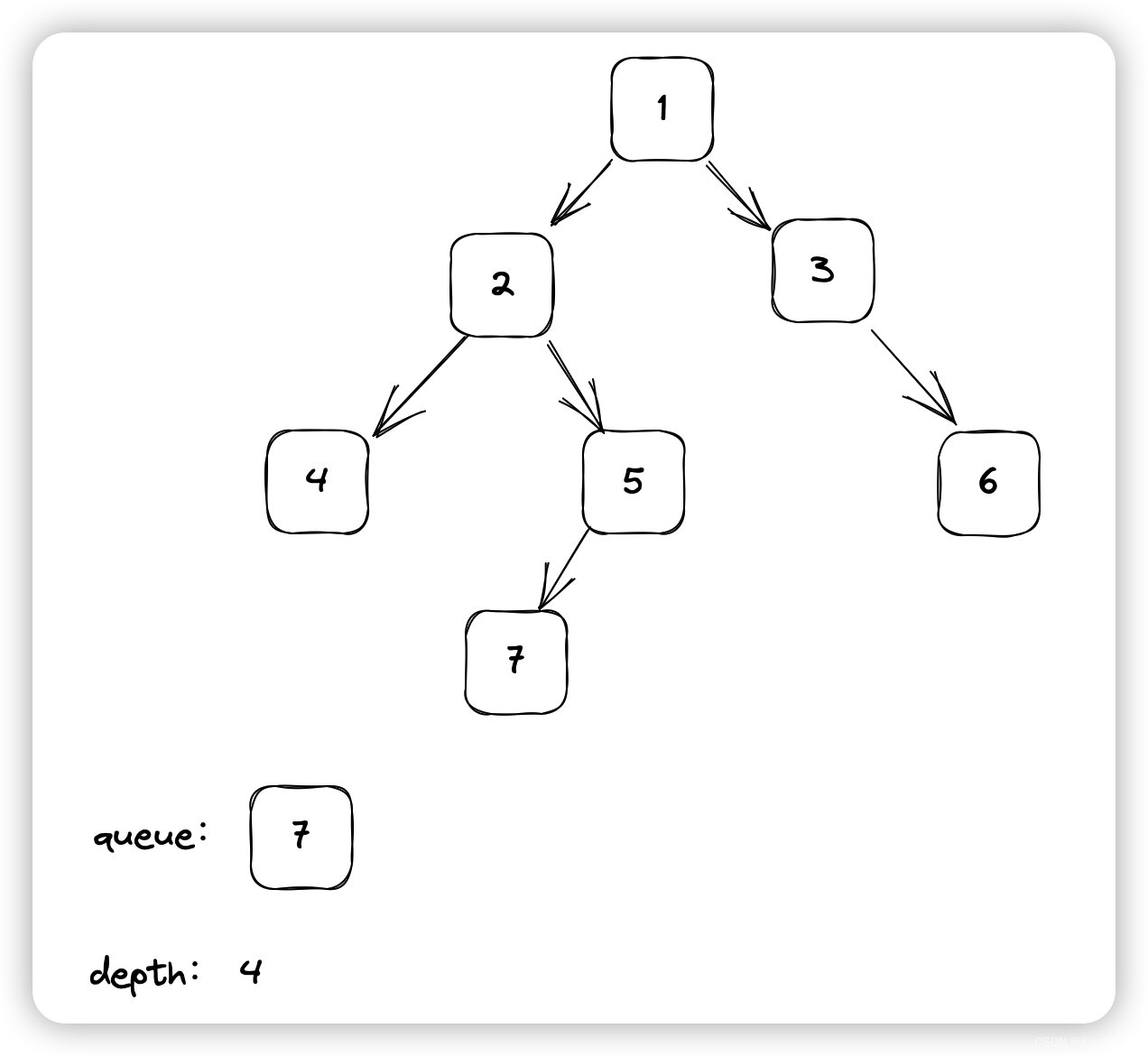
现在queue的长度是1,弹出1个元素,此时该元素左子树和右子树都为null,不再向队列中添加元素,循环结束,depth = 4
方法一完整代码
import java.util.*;
/**
public class TreeNode {int val = 0;TreeNode left = null;TreeNode right = null;public TreeNode(int val) {this.val = val;}}
*/
public class Solution {public int TreeDepth(TreeNode root) {if(root == null){return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.add(root);int depth = 0;while(!queue.isEmpty()) {int size = queue.size();depth++;for (int i = 0; i < size; i++) {TreeNode cur = queue.poll();if (cur.left != null) {queue.add(cur.left);}if(cur.right != null){queue.add(cur.right);}}}return depth;}
}思路二
深度优先搜索,分别确定左右子树中深度的较大值
使用递归分别确定节点的左子树高度和右子树高度,每次递归到下一层节点都需要将depth + 1,如果此时depth的长度大于max,就将max的值更新为depth,这样就可以返回左右子树高度的较大者
方法二完整代码
/**
public class TreeNode {int val = 0;TreeNode left = null;TreeNode right = null;public TreeNode(int val) {this.val = val;}
}
*/
public class Solution {public int TreeDepth(TreeNode root) {if(root == null){return 0;}int depth = 0;int[] max = new int[1];max[0] = 0;TreeDepthHelper(root, depth, max);return max[0];}private void TreeDepthHelper(TreeNode root, int depth, int[] max) {if(root == null){if(max[0] < depth){max[0] = depth;}return;}TreeDepthHelper(root.left, depth + 1, max);TreeDepthHelper(root.right, depth + 1, max); }
}
思路三
和思路二类似,形式上更容易理解
我们认为最下面的空指针null为第0层,往上走每层加一
因此,我们只需要统计左子树的高度和右子树高度中的较大值,然后再加1即可得到当前节点的高度
方法三完整代码
public int TreeDepth(TreeNode root) {if (root == null){return 0;}return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
}
相关文章:

Java——二叉树的深度
题目链接 牛客网在线oj题——二叉树的深度 题目描述 输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度,根节点的深度视为 1 。 数据范围&am…...
)
一般现在时(二)
一般现在时(二) 1.什么叫实义动词? 实义动词是指表示有具体意思的动词,也叫行为动词。 例如:like(喜欢) eat(吃) live(居住) have(有) run(跑)等等。 实义动词占英语中动词的绝大多数 🔖我们已学过的be动词可译为是,有时译为成为,有时则没有具体意…...

leetcode657. 机器人能否返回原点
题目描述解题思路执行结果 leetcode657. 机器人能否返回原点 题目描述 机器人能否返回原点 在二维平面上,有一个机器人从原点 (0, 0) 开始。给出它的移动顺序,判断这个机器人在完成移动后是否在 (0, 0) 处结束。 移动顺序由字符串 moves 表示。字符 mov…...

DAY 48 Nginx的 location与rewrite模块
[正则表达式] 常用的[Nginx] 正则表达式 $ :匹配输入字符串的结束位置* :匹配前面的字符零次或多次。如“ol*”能匹配“o”及“ol”、“oll” :匹配前面的字符一次或多次。如“ol”能匹配“ol”及“oll”、“olll”,但不能匹配“…...

Linux 常用操作技巧
Linux 操作技巧大全 Linux是一种强大的操作系统,掌握各种操作技巧可以帮助我们惬意地使用它。在这篇博客中,我们将分享一些实用的Linux技巧,希望能对您有所帮助! 1. 使用Tab进行自动补全 在输入命令时,按下Tab键可…...
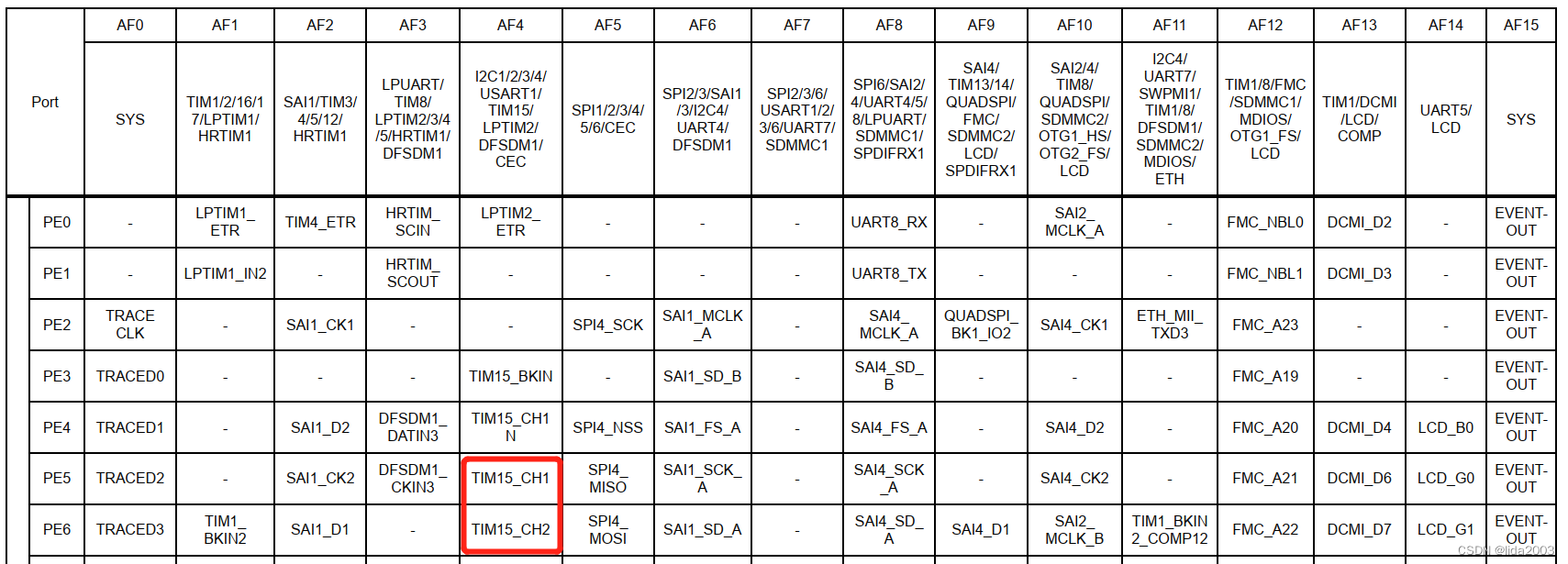
BetaFlight统一硬件配置文件研读之timer命令
BetaFlight统一硬件配置文件研读之timer命令 1. 源由2. 代码分析3. 实例分析4. 配置情况4.1 AFn配置查表4.2 timer4.3 timer show4.4 timer pin list 5. 参考资料 统一硬件配置文件的设计是一种非常好的设计模式,可以将硬件和软件的工作进行解耦。 1. 源由 cli命令…...
码出高效:Java开发手册笔记(java对象四种引用关系及ThreadLocal)
码出高效:Java开发手册笔记(java对象四种引用关系及ThreadLocal) 前言一、引用类型二、ThreadLocal价值三、ThreadLocal副作用 前言 “水能载舟,亦能覆舟。”用这句话来形容 ThreadLocal 最贴切不过。ThreadLocal 初衷是在线程并…...
为什么要进行数据决策?数据决策对企业而言有何重要意义?
“大数据”几乎已成为时下最时髦的词汇,不夸张地说,当今各行各业无不对大数据充满了向往,希望自己在新一轮的大数据营销中抢占先机。同时,从大数据中引申出的数据挖掘、数据分析、数据安全等数据运用技术也成为人们热捧的焦点。 …...

2. Java 异常体系
2.1 Throwable java.lang.Throwable 类是 Java 程序执行过程中发生的异常事件对应的类的根父类。 Throwable 中的常用方法: public void printStackTrace():打印异常的详细信息。 包含了异常的类型、异常的原因、异常出现的位置、在开发和调试阶段都得…...

如何学好STM32,需要哪些步骤?
学习STM32应用于项目开发需要以下步骤: 学习STM32的基本知识:包括STM32的架构、寄存器、外设等,理解STM32的工作原理和基本操作方法。 学习嵌入式系统和RTOS的基础知识:了解嵌入式系统的概念、RTOS的基本原理和使用方法ÿ…...
)
武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 x 3 \int \frac{\rm dx}{1x^3} ∫1x3dx 解法一: 待定系数法: ∫ d x 1 x 3 \int \frac{dx}{1x^3} ∫1x3dx ∫ d x ( 1 x ) ( x 2 − x 1 ) \int \frac{dx}{(1x)(x^2-x1)} ∫(1x)(x2−x1)dx 1 3 ∫ ( 1 x 1 − x 2 x 2 − x …...

记一次产线打印json导致的redis连接超时
服务在中午十一点上线后,服务每分钟发出三到四次redis连接超时告警。错误信息为: Dial err:dial tcp: lookup xxxxx: i/o timeout 排查过程 先是检查redis机器的情况,redis写入并发数较大,缓存中保留了一小时大概400w条数据。red…...

FPGA入门系列12--RAM的使用
文章简介 本系列文章主要针对FPGA初学者编写,包括FPGA的模块书写、基础语法、状态机、RAM、UART、SPI、VGA、以及功能验证等。将每一个知识点作为一个章节进行讲解,旨在更快速的提升初学者在FPGA开发方面的能力,每一个章节中都有针对性的代码…...

【三十天精通Vue 3】第二十六天 Vue3 与 TypeScript 最佳实践
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、为什么使用TypeScript?二、Vue 3和TypeScript…...

ffmpeg-mov-metadate不识别Bug修复
文章目录 BUG起因类似问题反馈问题解决具体步骤: 阅读过文章ffmpeg命令行解析调试流程记录movenc.c源码分析 BUG起因 在ffmpeg参数默认可识别的metadata参数如下: 具体可见libavformat/movenc.c->mov_write_udta_tag() mov_write_string_metadata(s,…...
(8.6) 引导程序更新)
(8)(8.6) 引导程序更新
文章目录 前言 1 我在哪里可以下载最新的引导程序? 2 使用任务规划器进行升级...
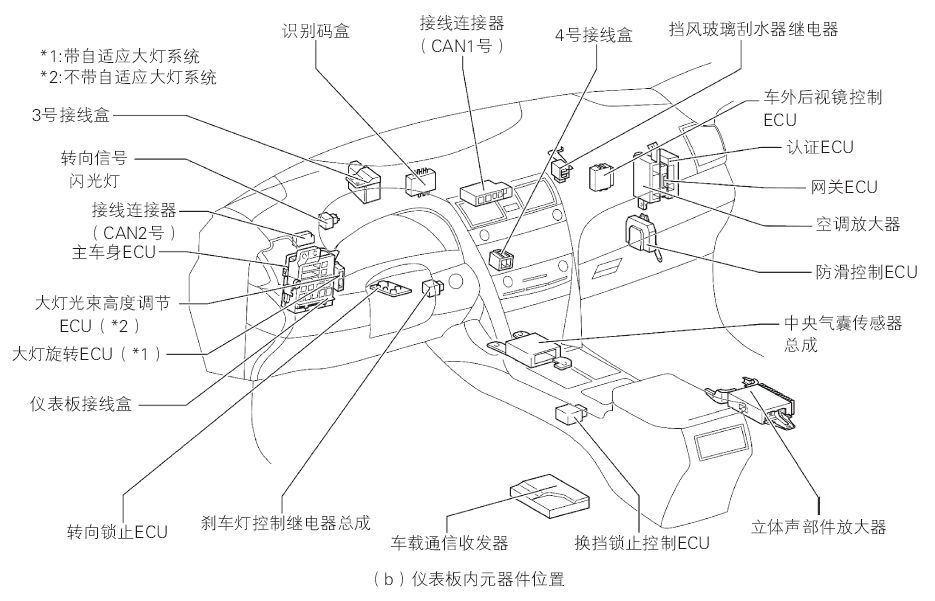
汽车电路图、原理框图、线束图、元器件布置图的识读技巧与要点
摘要: 想要读懂汽车电路图就必须把电的通路理清楚,即某条线是什么信号,该信号是输入信号、输出信号还是控制信号以及信号起什么作用,在什么条件下有信号,从哪里来,到哪里去。 一、汽车电路图的识读技巧 1.…...
( 数组和矩阵) 667. 优美的排列 II ——【Leetcode每日一题】
❓667. 优美的排列 II 难度:中等 给你两个整数 n 和 k ,请你构造一个答案列表 answer ,该列表应当包含从 1 到 n 的 n 个不同正整数,并同时满足下述条件: 假设该列表是 answer [a1, a2, a3, ... , an] ࿰…...

【python基础语法七】python内置函数和内置模块
内置全局函数 abs 绝对值函数 print(abs(-1)) # 1 print(abs(100)) # 100round 四舍五入 """奇进偶不进(n.5的情况特定发生)""" res round(3.87) # 4 res round(4.51) # 5 # res round(2.5) # 2 # res round(3.5) # 4 res round(6.5) # …...

81. read readline readlines 读取文件的三种方法
81. read readline readlines 读取文件的三种方法 文章目录 81. read readline readlines 读取文件的三种方法1. 读取文件的三种方法2. read方法3. readline方法4. readlines方法5. 代码总结5.1 read方法读取全部内容5.2 readline方法读取一行,返回字符串5.3 readli…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
