瑞吉外卖：后台系统登录功能
文章目录
- 需求分析
- 代码开发
- 创建实体类
- 导入返回结果类R
- controller、service与mapper
- login.html
需求分析
点击登录按钮后，浏览器以POST方式向employee/login提交username和password，服务器经过处理后向浏览器返回某种格式的数据，其中包含：
- code：登录状态码
- data：用户信息
- msg：失败原因
代码开发
创建实体类
创建实体类Employee，与数据库中的表employee进行映射，直接导入写好的java文件到entity目录
在application.yml中开启映射时的命名转换
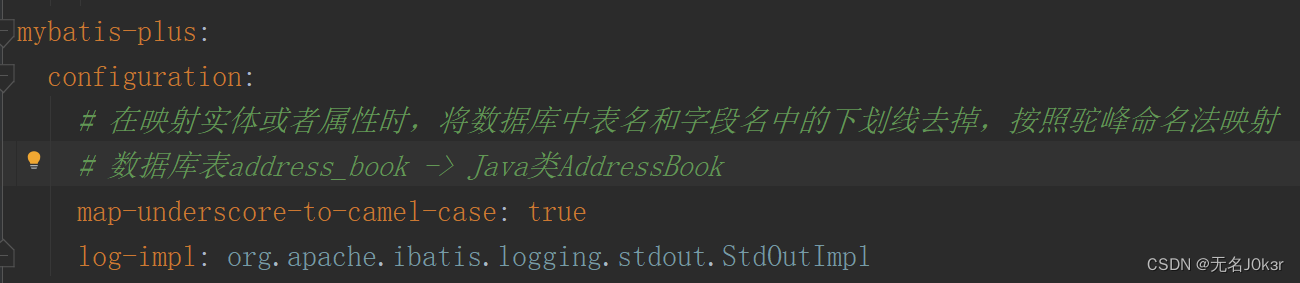
导入返回结果类R
R是一个通用结果类，所有服务器返回的数据都包装为此种类型返回给前端。
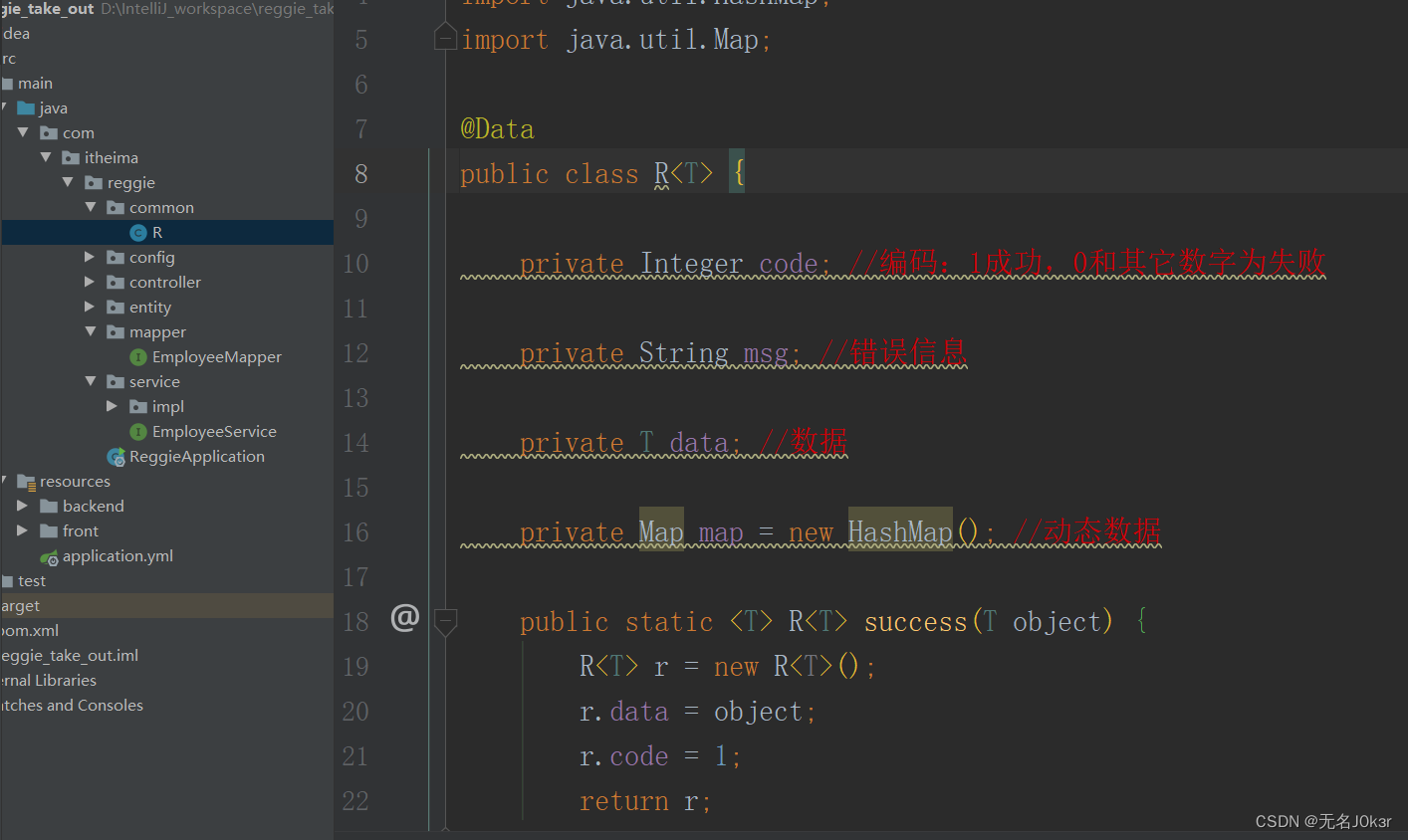
controller、service与mapper
- controller调用ServiceImpl里封装好的方法为浏览器提供访问服务。
- service提供业务逻辑使用的方法，其实现在ServiceImpl中。
- mapper为ServiceImpl提供了操作数据的方法，具体实现的SQL语句在xml文件中。
login.html
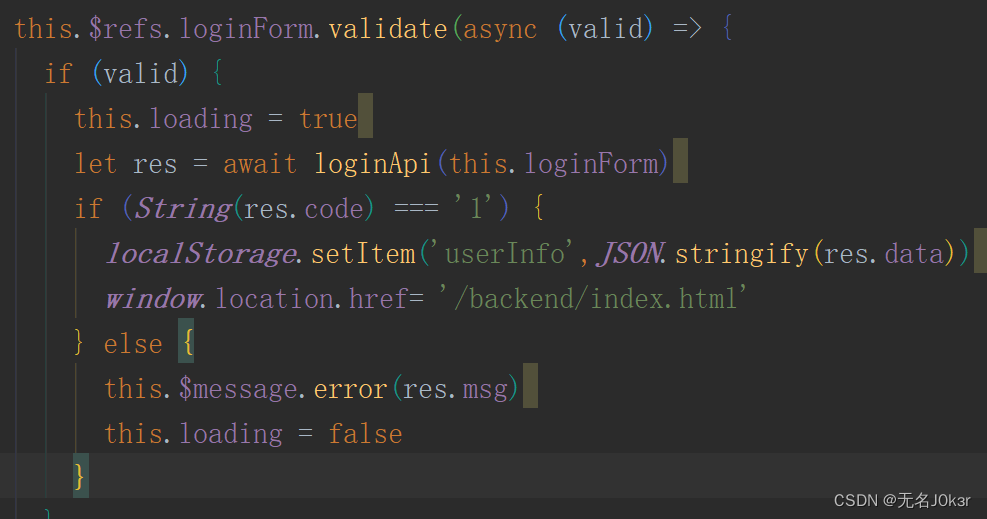
valid是密码位数校验
通过校验后页面登录按钮显示为登陆中
下图为Spring框架将后端返回的R对象转成的json，返回到浏览器，也即下文的res
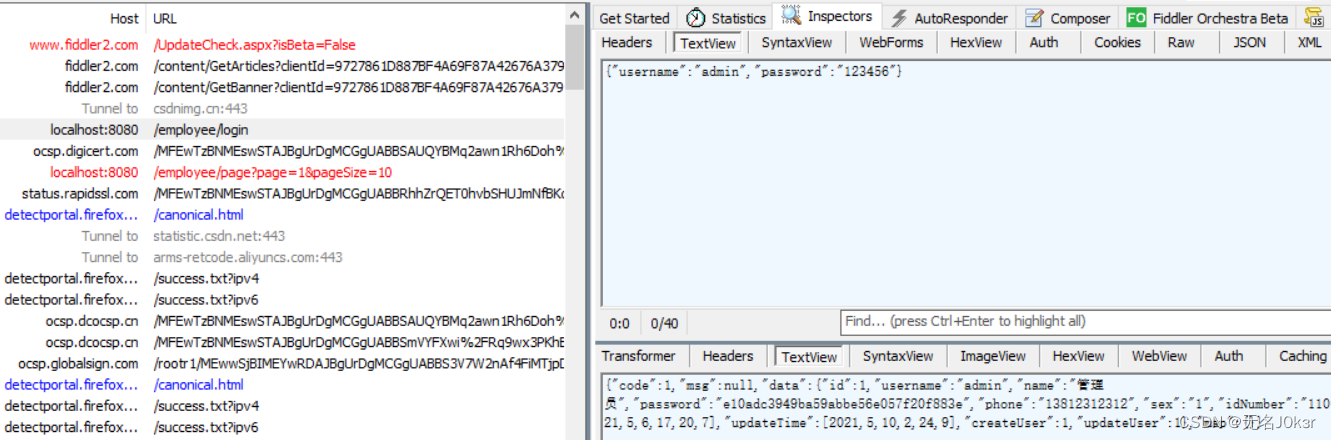
若res中code为1，则表示登录成功，
将res的data转json存到localStorage中
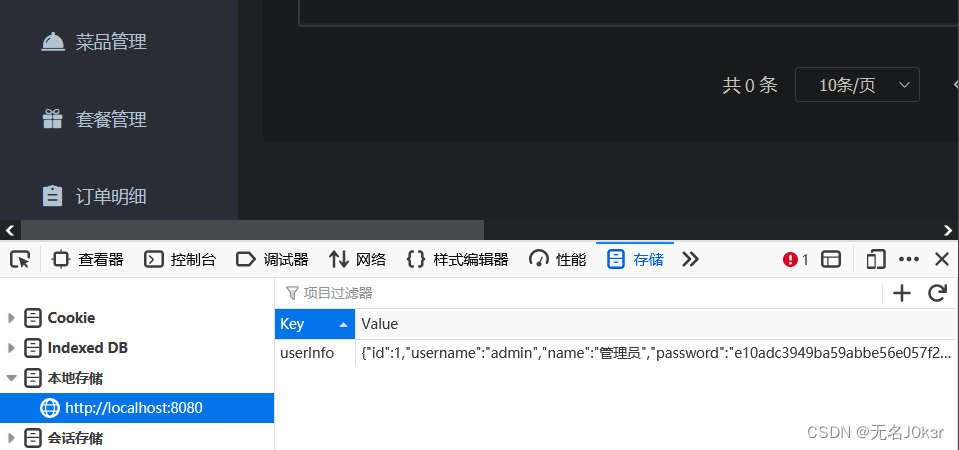
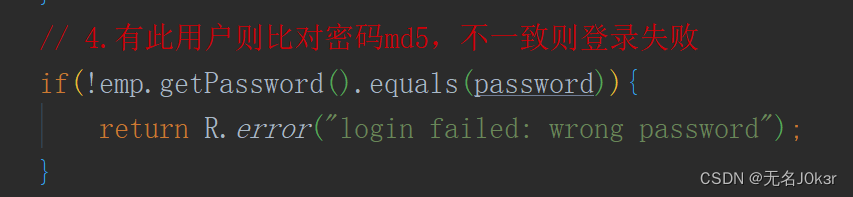
如果登录失败，则提取res的msg显示在页面上。
相关文章：
瑞吉外卖：后台系统登录功能
文章目录 需求分析代码开发创建实体类导入返回结果类Rcontroller、service与mapperlogin.html 需求分析 点击登录按钮后，浏览器以POST方式向employee/login提交username和password，服务器经过处理后向浏览器返回某种格式的数据，其中包含&…...
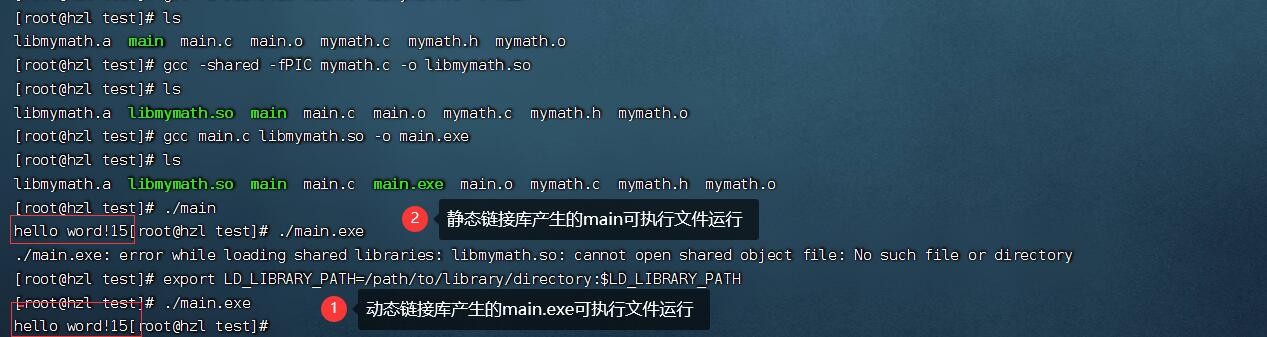
Linux拓展：链接库
一.说明 本篇博客介绍Linux操作系统下的链接库相关知识，由于相关概念已在Windows下链接库一文中介绍，本篇博客直接上操作。 二.静态链接库的创建和使用 1.提前看 这里主要介绍的是C语言的链接库技术，而在Linux下实现C语言程序，…...
基于.Net开发的、支持多平台、多语言餐厅点餐系统
今天给大家推荐一套支持多平台、多语言版本的订单系统，适合餐厅、酒店等场景。 项目简介 这是基于.Net Framework开发的，支持手机、平板、PC等平台、多语言版本开源的点餐系统，非常适合餐厅、便利店、超市、酒店等，该系统基础功…...
Windows系统SSL/TLS安全协议介绍
支持安全加密的https底层使用的就是SSL/TLS，在发起https请求之前需要先建立TCP连接，之后再进行SSL/TLS协议协商，协商通过后才能发起https请求。本文将详细介绍SSL/TLS协议相关的内容。 之前在项目中就出现过客户端SSL/TLS版本过低，导致向服务器发起连接时被服务器拒绝的问题…...
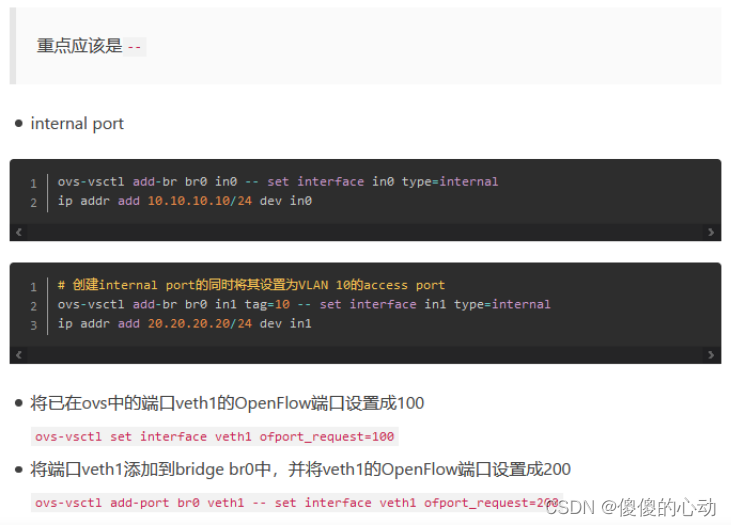
ovs-vsctl 命令详解
ovs-vsctl 命令详解 网桥Bridge 创建 Bridge ovs-vsctl add-br br0 删除 Bridge ovs-vsctl del-br br0 列出 Bridge ovs-vsctl list-br 显示详情 ovs-vsctl show 端口 Port 添加端口 ovs-vsctl add-port br0 p1 其中br0 为上面添加的bridge p1可以是物理端口或者vN…...
具备“记忆”功能的VBA目录选择器
大家使用任意一款浏览器（例如：Chrome、Edge）下载文件时，如果【另存为】对话框选择C:\Download，那么下次再次使用【另存为】功能，对话框默认显示C:\Download，而不是根目录。 在VBA开发中调用目录…...
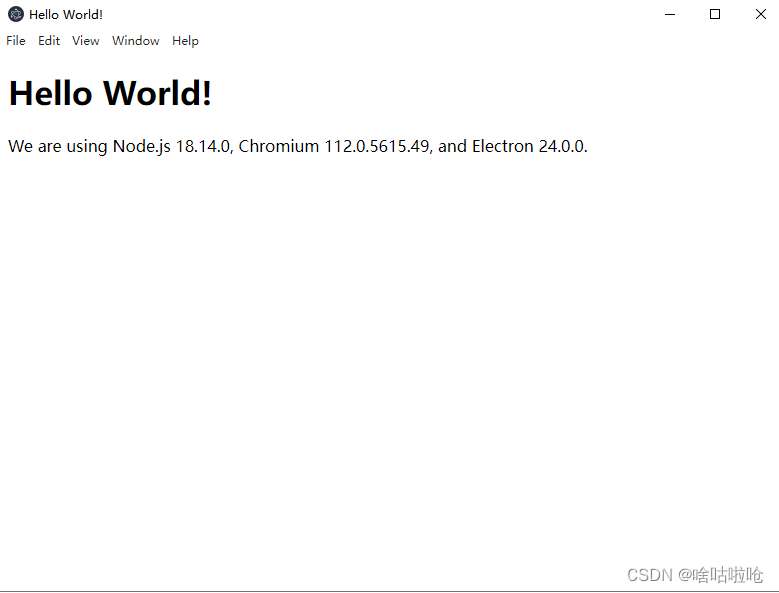
electron入门 | 手把手带electron项目初始化
Electron是一个基于Chromium和 Node.js，可以使用 HTML、CSS和JavaScript构建跨平台应用的技术框架，兼容 Mac、Windows 和 Linux。 目录 1.了解electron 2.开发环境 3.初始化 采坑插曲： 1.了解electron Electron 可以让你使用纯 JavaScrip…...
力扣解法汇总2423. 删除字符使频率相同
目录链接： 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目： https://github.com/September26/java-algorithms 原题链接：力扣 描述： 给你一个下标从 0 开始的字符串 word ，字符串只包含小写英文字母。你…...
【超算/先进计算学习】日报8
目录 今日已完成任务列表遇到的问题及解决方案任务完成详细笔记阶段一阶段二阶段三阶段四 对自己的表现是否满意简述下次计划其他反馈 今日已完成任务列表 超算/高性能计算总结 遇到的问题及解决方案 无 任务完成详细笔记 阶段一 在学习的第一阶段，我们首先对需要…...
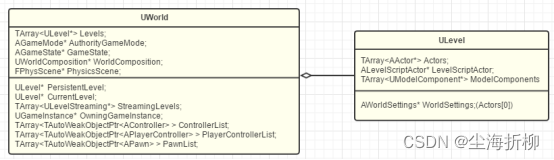
《LearnUE——基础指南:上篇—2》——GamePlay架构之Level和World
目录 听说世界是由多个Level组成的 1.2.1 引言 1.2.2 建造大陆（ULevel） 1.2.3构建世界（World） 1.2.4总结 听说世界是由多个Level组成的 1.2.1 引言 上小节谈到Actor和Component的关系，UE利用Actor的概念组成了世…...
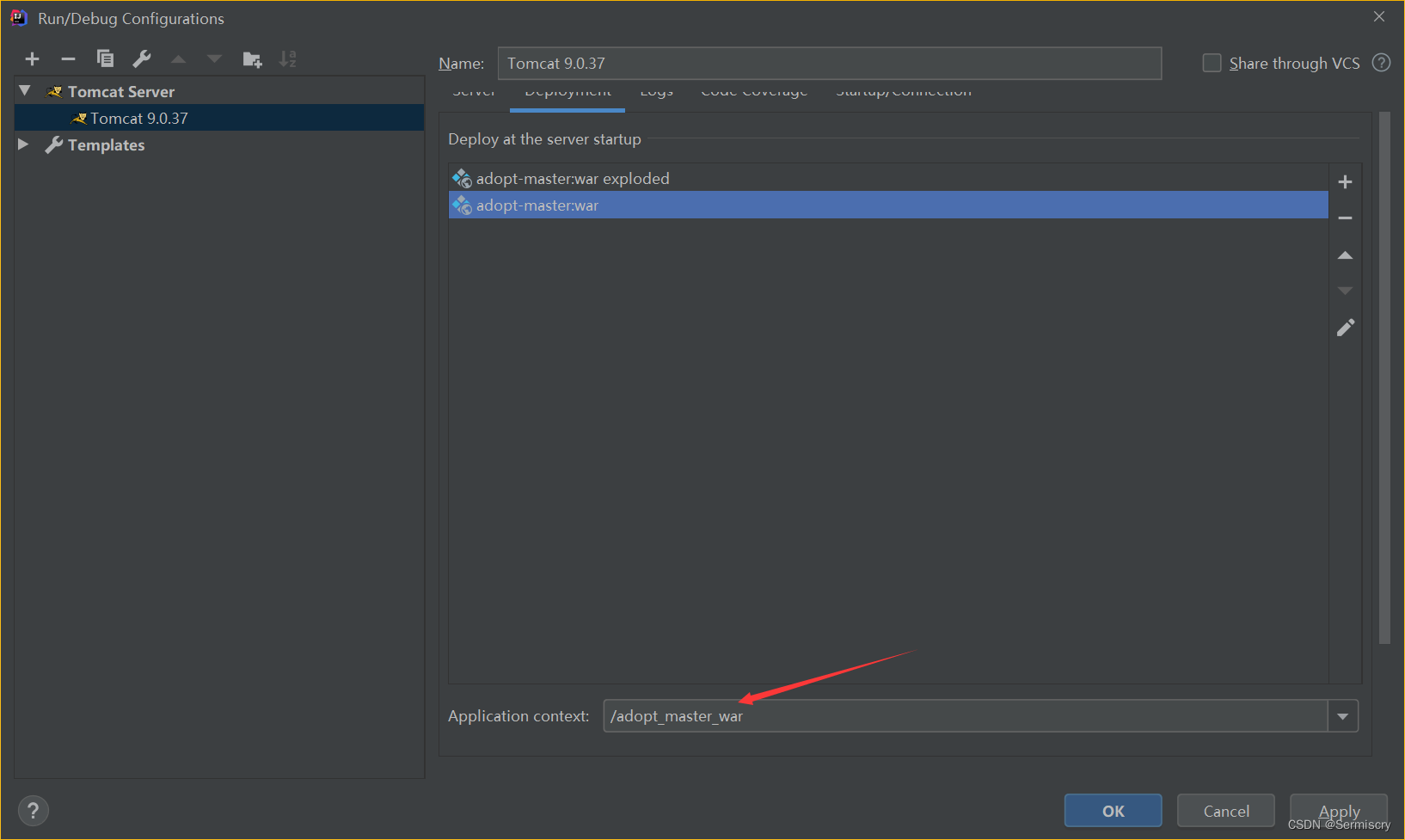
IDEA部署tomcat项目
文章目录 只是部署一下看到这里即可war和war exploded的区别warwar exploded update的动作update resourcesupdate classes and resourcesredeployrestart server 解决了拿到了一个tomcat项目后如何将它部署到IDEA里面的问题。 file->open 选中pom.xml并open as project …...
IAM角色
Identity-based policy，它关联到特定的User/Role/Group上，指定这些主体能对哪些资源进行怎样的操作 Resource-based policy，它关联到具体的AWS资源上，指定哪些主体可以对这个资源做怎样的操作 aws受信任关系视为aws服务可以实现&a…...
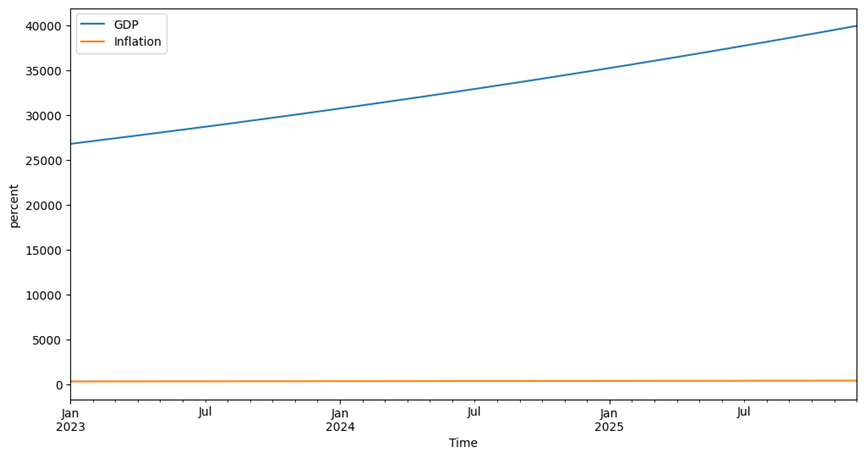
【VAR | 时间序列】以美国 GDP 和通货膨胀数据为例的VAR模型简单实战（含Python源代码）
以美国 GDP 和通货膨胀数据为例： 1. 数据集 下载数据我们需要从 FRED 数据库下载美国 GDP 和通货膨胀数据，并将它们存储在 CSV 文件中。可以在 FRED 网站（https://fred.stlouisfed.org/）搜索并下载需要的数据。在这里࿰…...
常用的设计模式之二（行为型模式）
文章目录 观察者模式模板模式 观察者模式 观察者模式是一种行为型设计模式，它定义了一种一对多的依赖关系，让多个观察者对象同时监听某一个主题对象，当主题对象发生变化时，它的所有观察者都会收到通知并进行相应的处理。 观察者…...
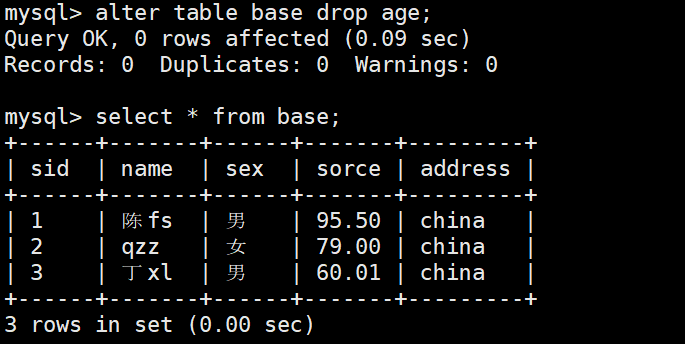
MYSQL基本操作（增删改查）
数据库的列类型 int：整型 用于定义整数类型的数据 float：单精度浮点4字节32位 准确表示到小数点后六位 double：双精度浮点8字节64位 char：固定长度的字符类 用于定义字符类型数据&…...
双周赛103（模拟、网格图BFS、树状数组）
文章目录 双周赛103[6406. K 个元素的最大和](https://leetcode.cn/problems/maximum-sum-with-exactly-k-elements/)模拟 [6405. 找到两个数组的前缀公共数组](https://leetcode.cn/problems/find-the-prefix-common-array-of-two-arrays/)模拟 [6403. 网格图中鱼的最大数目](…...
【数据结构】二叉树（详细）
二叉树 1.树1.1定义1.2基本术语1.3树形结构和线性结构1.4树的存储结构1.4.1双亲表示法1.4.2孩子兄弟表示法 2.二叉树2.1定义2.2特殊二叉树2.3性质2.4存储结构2.4.1顺序存储2.4.2链式存储结构 3.二叉树的基本操作3.1前序遍历（先序遍历）3.2中序遍历3.3后序…...
蓝牙耳机哪款性价比高一些？2023年性价比最高的蓝牙耳机推荐
随着科技的进步，蓝牙耳机已然成为我们生活中的一部分，无论是通勤、追剧、运动或者玩游戏，大都会用到蓝牙耳机。那么，哪款蓝牙耳机的性价比高一些？相信大多数人在选择产品的时候，都会看性价比。接下来&#…...
等保2.0存在的问题
等保制度和技术要求 国家信息安全等级保护制度（二级）相关要求包含技术要求和管理要求，技术要求包含：物理安全、网络安全、主机安全、应用安全及数据安全及备份恢复；管理要求包含：安全管理机构、安全管理制度、人员安全管理、系统建设管理、系统运维管理。 一、 技术要求 …...
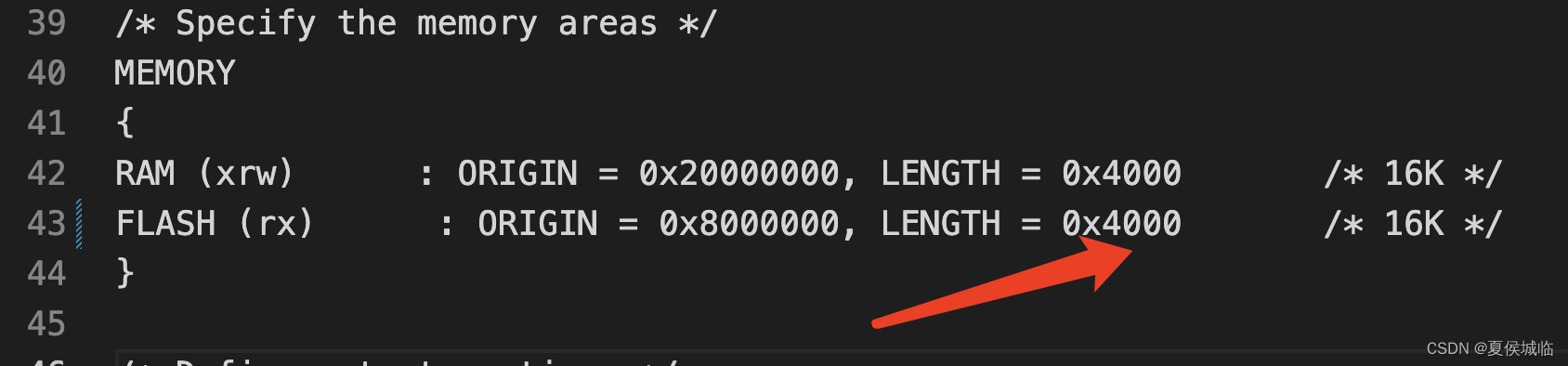
国民技术N32G430开发笔记（9）- IAP升级 Bootloader的制作
IAP升级 Bootloader的制作 1、上节提到Flash的分区，0x8000000-0x8004000为Boot分区，我们的bootloader就烧录到此分区。 Bootloader很简单，新建一个普通的工程， 也不用初始化外部设备，开机后，直接跳转到 A…...
观成科技：隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具，该工具基于TUN接口实现其功能，利用反向TCP/TLS连接建立一条隐蔽的通信信道，支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式，适应复杂网…...
rknn优化教程（二）
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK，开始写第二篇的内容了。这篇博客主要能写一下： 如何给一些三方库按照xmake方式进行封装，供调用如何按…...
反向工程与模型迁移：打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下，商品详情API作为连接电商平台与开发者、商家及用户的关键纽带，其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息（如名称、价格、库存等）的获取与展示，已难以满足市场对个性化、智能…...
连锁超市冷库节能解决方案：如何实现超市降本增效
在连锁超市冷库运营中，高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术，实现年省电费15%-60%，且不改动原有装备、安装快捷、…...
条件运算符
C中的三目运算符（也称条件运算符，英文：ternary operator）是一种简洁的条件选择语句，语法如下： 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true，则整个表达式的结果为“表达式1”…...
linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 （忘了有没有这步了 估计有） 刷机程序 和 镜像 就不提供了。要刷的时…...
oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异，它们的数据同步要求既要保持数据的准确性和一致性，又要处理好性能问题。以下是一些主要的技术要点： 数据结构差异 数据类型差异ÿ…...
MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域，MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步，这两种通讯协议也正在被逐步融合，形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
C++.OpenGL （10/64）基础光照（Basic Lighting）
基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接：3403. 从盒子中找出字典序最大的字符串 I 代码如下： class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...