工序排序问题--约翰逊法精讲
什么是约翰逊法?
约翰逊法是作业排序中的一种排序方法。选出最短加工时间i*,若最短加工时间有多个,任选1个.若i*出现在机床1,它对应的工件先安排加工,否则放在最后安排,安排后划去该工件,重复上两个步骤,直到所有工件都排序完毕。
约翰逊法适用的条件是:n个工件经过二、三台设备(有限台设备)加工,所有工件在有限设备上加工的次序相同。
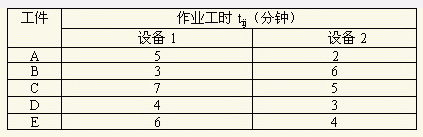
举例说明:有五个工件在二台设备上加工,加工顺序相同,现在设备1上加工,再在设备2上加工,工时列于下表1中,用约翰逊法排序。
表1 加工工时表
约翰逊法具体步骤
第一步,取出最小工时t12=2。如该工时为第一工序的,则最先加工;反之,则放在最后加工。此例是A工件第二工序时间,按规则排在最后加工。
第二步,将该已排序工作划去。
第三步,对余下的工作重复上述排序步骤,直至完毕。此时t21=t42=3,B工件第一工序时间最短,最先加工;D工件第二工序时间最短,排在余下的工件中最后加工。最后得到的排序为:B-C-E-D-A。整批工件的停留时间为27分钟。
1.约翰逊法的排列规则
如果满足mint1k;t2k < mint2k;t1k
则将k工件排在h工件之前。
式中:t1k、t2k:k工件第1工序、第2工序的加工时间;
t2k、t1k:h工件第2工序、第1工序的加工时间。
2.约翰逊排序法的进行步骤
(1)列出零件组的工序矩阵;
(2)在工序矩阵中选出加工时间最短的工序。如果改工序属于第1工序,则将该工序所属工件排在前面。反之,最小工序是第2工序,则将该工序所属的工件排在最后面。若最小的工序又多个,可任选其中的一个;
(3)将已排序的工件从工序矩阵中消去;
(4)继续按步骤(1)、(2)、(3)进行排序,若所有工件都已排定投产顺序,排序即告结束。
例:有6中零件,其工序矩阵见表
表:零件的工序矩阵
工件号 | 1 | 2 | 3 | 4 | 5 | 6 |
第1工序M1 | 6 | 2 | 9 | 4 | 4 | 5 |
第2工序M2 | 8 | 3 | 3 | 5 | 8 | 4 |
根据约翰逊法的排序步骤:
(1)按前工序最小的选出2号工件及后工序最小的选出3号工件前,3号排在后。从原工件矩阵中消去2号及3号零件,见下表。
项目 | 新工序矩阵 | 原工序矩阵 | ||||
工件号 | 2 | 3 | 1 | 4 | 5 | 5 |
第1工序M1 | 2 | 9 | 6 | 4 | 4 | 5 |
第2工序M2 | 3 | 3 | 8 | 5 | 8 | 4 |
(2)对原工件矩阵继续步骤(1)、(2)、(3),前工序最小的有4和5号两工件可任选其一,后工序最小的为6号工件。选出该两工件,并按前述规则排列,插入新工序矩阵见下表。
项目 | 新工序矩阵 | 原工序矩阵 | |||||
工件号 | 2 | 4 | 6 | 3 | 1 | 5 | |
第1工序M1 | 2 | 4 | 5 | 9 | 6 | 4 | |
第2工序M2 | 3 | 5 | 4 | 3 | 8 | 8 | |
(3)按规则继续进行排序,5号工件排在前,1号工件拍在后。
工序矩阵。表是按约翰逊法排序后的新工艺矩阵。
按约翰逊法排序后的新工艺矩阵
项目 | 新工序矩阵 | |||||
工件号 | 2 | 4 | 5 | 1 | 6 | 3 |
第1工序M1 | 2 | 4 | 6 | 5 | 9 | |
第2工序M2 | 3 | 5 | 8 | 8 | 4 | 3 |
对于同顺序排序问题,可以通过表上作业,计算全组零件的最大流程时间Fmax见表
最大流程时间Fmax计算表
工件号 | 2 | 5 | 4 | 1 | 6 | 3 |
第1工序M1 | 2/2 | 4/6 | 4/10 | 6/16 | 5/21 | 9/30 |
第2工序M2 | 3/5 | 5/11 | 8/19 | 8/27 | 4/31 | 3/34 |
表中斜线右方的数字是到该工序结束时的流程时间,它的计算方法如下:
到该工序结束时间的流程时间=该工序的开始时间+该工序的加工时间
在生产过程中一个工序的开始时间取决于两个因素:
该工序前一道工序的结束时间;
该工序所用的设备上紧前工件的加工结束时间。该工序的开始时间应取上述两数中之大者。例如,1号工件第2工件结束时的流程时间,应为Fj1m2=max{16;19}+8=27。
根据上表中的数据可得到一张1至6号工件的生产进度表,有每个工件在各台设备上的开工时间与完工时间。
本例中第4和第5号工件在被选时,由于前工序均为最小工序,当时任选了4号。如果选了5号结果有如何呢?见下表。
本例不同排序方案的最大流程计算
工件号 | 2 | 5 | 4 | 1 | 6 | 3 |
第1工序M1 | 2/2 | 4/6 | 4/10 | 6/16 | 5/21 | 9/30 |
第2工序M2 | 3/5 | 8/14 | 5/19 | 8/27 | 4/31 | 3/34 |
根据上面两表的计算结果,说明对于条件等价的条件,任选其中之一,不影响最后结果。按约翰逊法所排出的结果应为最优解,这里说明最优解可能不止一个,可以有多个等值的最优解。
约翰逊法只适用于两工序工件的排序问题,所以它的使用范围受到很大的限制。


某公司在一次火灾中损坏了5台仪器,这些仪器的修复需要经过如下两道工序:
(1)将损坏的仪器运至修理车间,拆卸开;
(2)清洗仪器部件,更换报废部分,装配,测试,并送回原车间。
每台仪器在两个工序的各自所需时间如表所示。两道工序分别由不同的人担当。由于原车间没有这5台仪器就无法恢复生产,所以希望找到一个较好的排序方案,使全部修理时间尽可能短。每台仪器在两个工序的各自所需时间如表所示。两道工序分别由不同的人担当。由于原车间没有这5台仪器就无法恢复生产,所以希望找到一个较好的排序方案,使全部修理时间尽可能短。

详细解题过程
(1)①选出最短时间为Y3工序2,时间为 3个单位
②Y3工序2在第二道工序,排在最后即第5位,队列中去掉Y3。
最后一道作业为 Y3工序。
(2) 剩余作业中最短时间工序为Y2工序1,用时4个单位,在第一道工序,所以Y2作业排在第1位,等待序列中去掉Y2。
(3) 剩余作业中最短时间工序为Y5工序2,用时8个单位,在第二道工序,所以Y5作业排在第4位,等待队列中去掉Y5。
(4) 剩余作业中最短时间工序为Y1工序1,用时12个单位,在第一道工序,所以Y1作业排在第2位。
(5) 剩余作业Y4作业排在第3位。
所以作业顺序为 Y2 Y1 Y4 Y5 Y3。

原则:1、找最小值min,如果min是前道工序,则该作业放最前;
若min是后道工序,则该作业放最后。从等待队列删除该作业。
2、如果有多个值相等,则可以任意选择。
Johnson算法解题思路
1、选择最短的作业时间
2、如果最短时间的作业在第一个加工中心,则安排在最前面,若在第二个加工中心,则安排在最后面。在等待的队列中,将该作业删除
3、重复1、2步。
相关文章:

工序排序问题--约翰逊法精讲
什么是约翰逊法?约翰逊法是作业排序中的一种排序方法。选出最短加工时间i*,若最短加工时间有多个,任选1个.若i*出现在机床1,它对应的工件先安排加工,否则放在最后安排,安排后划去该工件,重复上两个步骤,直…...

WebDAV之葫芦儿·派盘+网盘精灵
网盘精灵 支持WebDAV方式连接葫芦儿派盘。 推荐一款让您的iPhone、iPod、iPad 变成WebDav客户端的软件,支持从WebDav服务器连接葫芦儿派盘服务进行上传和下载件。 网盘精灵让您的iPhone、iPod、iPad 变成WebDav客户端。功能:WebDav操作、文件共享、本地文件管理...

计算机网络期末知识点总结
计算机网络期末知识点总结第四章—网络层:数据面4.1概述4.2虚电路和数据报网络4.3路由器工作原理4.4网际协议:因特网中的转发和编址第五章 网络层:控制面5.1路由选择算法5.2路由器中的路由选择5.3广播和多播路由选择第六章 链路层(…...

【Vue3 组件封装】vue3 轮播图组件封装
文章目录轮播图功能-获取数据轮播图-通用轮播图组件轮播图-数据渲染轮播图-逻辑封装轮播图功能-获取数据 目标: 基于pinia获取轮播图数据 核心代码: (1)在types/data.d.ts文件中定义轮播图数据的类型声明 // 所有接口的通用类型 export typ…...
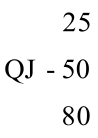
电力国家(行业)标准目录
1、3~63kV交流高压负荷开关 GB 3804-90 代替 GB 3804-882、电气装置安装工程35kV及以下架空电力线路施工及验收规范Code for construction and acceptance of 35kVand umder over head power levels electricequipment installation engineeringGB50173—923、带电作…...

如何实现倒序输出
问题 如何实现字符串的大小写转换并倒序输出。 方法 采用Java自带的类方法进行倒序。 package homework4; public class Blog09 { public static void main(String[] args) { String a "HelloWord"; String a2 a.toUpperCase(); String a3 …...

遗留系统的自动化测试策略和实践方法
1 什么是遗留系统 遗留系统是一种旧的方法、旧的技术、旧的计算机系统或应用程序,属于或与以前的、过时的计算机系统有关,但仍在使用中。通常,将系统称为“遗留系统”意味着它可能已经过时或需要更换,但是系统还在对外提供服务,还在不断的迭代,有新的需求不断的交付。Ma…...

【Android】系统源码下载及编译
源码及编译 步骤 1:创建一个空目录来存放源码: mkdir aosp cd aosp步骤 2:获取最新版本的 repo 并签出 android-8.1.0_r1 分支: repo init -u https://android.googlesource.com/platform/manifest -b android-8.1.0_r1其中&am…...
基于HTML实现浪漫情人节表白代码(附源代码)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

PCL 平面拟合——RANSAC
文章目录 一、基本思想二、代码示例1、参数选择2、核心代码3、完整代码4、结果展示三、关于 RANSAC 的一些思考参考文献一、基本思想 随机抽样一致性算法RANSAC(Random sample consensus)是一种迭代的方法,从一系列包含有离群值的数据中计算数学模型参数的方法。RANSAC算法本…...

【Linux之Shell脚本实战】监控系统的磁盘空间使用率
【Linux之Shell脚本实战】监控系统的磁盘空间使用率 一、脚本要求二、检查本地系统环境1.检查系统版本2.检查系统内核版本三、编写disk.sh脚本1.创建脚本目录2.编写disk.sh脚本3.执行测试脚本四、查看脚本执行日志文件五、本次实践总结1.脚本定时执行2.实践总结一、脚本要求 1.…...
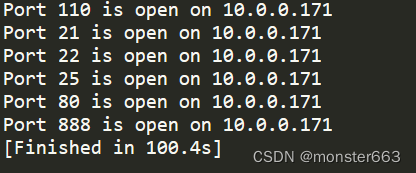
【Python安全编程】Python实现网络主机和端口扫描
文章目录前言环境准备Python实现主机扫描基于ARP协议基于ICMP协议普通版本多线程版本Python实现端口扫描扫描单个端口利用多线程扫描端口后记前言 本文主要讲几个利用Python实现网络扫描的小例子,可以结合多线程或多进程编程改进实例 我曾经走过多遥远的路 跨越过多…...
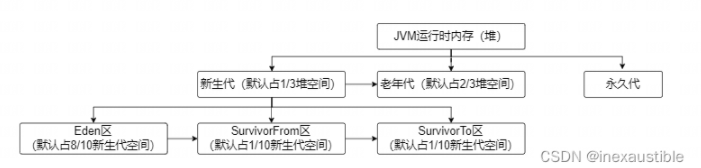
四大垃圾回收算法七大垃圾回收器
JVM的运行时内存也叫做JVM堆,从GC的角度可以将JVM分为新生代、老年代和永久代。其中新生代默认占1/3堆内存空间,老年代默认占2/3堆内存空间,永久代占非常少的对内存空间。新生代又分为Eden区、SurvivorFrom区和SurvivorTo区, Eden…...
P1217 [USACO1.5]回文质数 Prime Palindromes
[USACO1.5]回文质数 Prime Palindromes 题目描述 因为 151151151 既是一个质数又是一个回文数(从左到右和从右到左是看一样的),所以 151151151 是回文质数。 写一个程序来找出范围 [a,b](5≤a<b≤100,000,000)[a,b] (5 \le a < b \l…...
用大白话给你科普,到底什么是 API(应用程序编程接口)?
何为API?如果你在百度百科上搜索,你会得到如下结果:API(Application Programming Interface,应用程序编程接口)是一些预先定义的函数,目的是提供应用程序与开发人员基于某软件或硬件得以访问一组…...
企业电子招采系统源码——信息数智化招采系统
信息数智化招采系统 服务框架:Spring Cloud、Spring Boot2、Mybatis、OAuth2、Security 前端架构:VUE、Uniapp、Layui、Bootstrap、H5、CSS3 涉及技术:Eureka、Config、Zuul、OAuth2、Security、OSS、Turbine、Zipkin、Feign、Monitor、…...
)
【vnc】Ubuntu20.04+vnc安装和配置(中文输入法)
Ubuntu20.04vnc安装和配置(中文输入法) 安装vnc 用以下apt 命令安装: sudo apt install tigervnc-common tigervnc-standalone-server tigervnc-viewer tigervnc-xorg-extension注意,要用standalone-server版本,不要下载Tiger官方安装包&a…...

【排序算法】数据结构排序详解
前言: 今天我们将讲解我们数据结构初阶的最后一部分知识的学习,也是最为“炸裂”的知识---------排序算法的讲解!!!! 目录1.排序的概念及其运用1.1排序的概念1.2排序运用2.常见排序算法的实现2.1 插入排序2…...

【docker知识】DockerFile语法 1:注释指令、解释器指令
一、说明 在docker的指令下工作,似乎很简单,然而,对于复杂工程,这些初级知识是不够的。正确使用DockerFile构建镜像是必须的技能。我们这里假定您已经熟练docker的指令,我们继续上升一个台阶,如何用build和…...
)
[失业前端恶补算法]JavaScript leetcode刷题top100(一)
专栏声明:只求用最简单的,容易理解的方法通过,不求优化,不喜勿喷 今天更新五个 easy 难度题目: 两数之和 题面 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
