简单的无理函数的不定积分
前置知识:
- 直接积分法
- 有理函数的不定积分
简单的无理函数的不定积分
对无理函数积分的基本方法就是通过换元将其化为有理函数的积分。下面讲讲几类无理函数积分的求法。
注: R ( u , v ) R(u,v) R(u,v)是由 u , v u,v u,v与常数经过有限次四则运算得到的有理式。
形如 ∫ R ( x , a x + b c x + d ) d x \int R(x,\sqrt\dfrac{ax+b}{cx+d})dx ∫R(x,cx+dax+b)dx的积分
求形如 ∫ R ( x , a x + b c x + d ) d x \int R(x,\sqrt\dfrac{ax+b}{cx+d})dx ∫R(x,cx+dax+b)dx的积分,其中 a d ≠ b c ad\neq bc ad=bc。
令 t n = a x + b c x + d t^n=\dfrac{ax+b}{cx+d} tn=cx+dax+b,则 x = d t n − b a − c t n x=\dfrac{dt^n-b}{a-ct^n} x=a−ctndtn−b, d x = a d − b c ( a − c t n ) 2 n t n − 1 d t dx=\dfrac{ad-bc}{(a-ct^n)^2}nt^{n-1}dt dx=(a−ctn)2ad−bcntn−1dt,从而把原积分变换为有理函数的积分。
∫ R ( x , a x + b c x + d ) d x = ∫ R ( d t n − b a − c t n , t ) ⋅ a d − b c ( a − c t n ) 2 n t n − 1 d t \int R(x,\sqrt\dfrac{ax+b}{cx+d})dx=\int R(\dfrac{dt^n-b}{a-ct^n},t)\cdot\dfrac{ad-bc}{(a-ct^n)^2}nt^{n-1}dt ∫R(x,cx+dax+b)dx=∫R(a−ctndtn−b,t)⋅(a−ctn)2ad−bcntn−1dt
例题
计算 ∫ 1 ( x − 1 ) ( x + 1 ) 2 3 d x \int \dfrac{1}{\sqrt[3]{(x-1)(x+1)^2}}dx ∫3(x−1)(x+1)21dx
解:
\qquad 令 t = x + 1 x − 1 3 t=\sqrt[3]{\dfrac{x+1}{x-1}} t=3x−1x+1,则 x = t 3 + 1 t 3 − 1 x=\dfrac{t^3+1}{t^3-1} x=t3−1t3+1, d x = − 6 t 2 ( t 3 − 1 ) 2 d t dx=-\dfrac{6t^2}{(t^3-1)^2}dt dx=−(t3−1)26t2dt,于是
\qquad 原式 = ∫ x + 1 x − 1 3 ⋅ 1 x + 1 d x = − ∫ t ⋅ ( 1 2 ⋅ t 3 − 1 t 3 ) ⋅ 6 t 2 ( t 3 − 1 ) 2 d t =\int \sqrt[3]{\dfrac{x+1}{x-1}}\cdot\dfrac{1}{x+1}dx=-\int t\cdot(\dfrac 12\cdot\dfrac{t^3-1}{t^3})\cdot \dfrac{6t^2}{(t^3-1)^2}dt =∫3x−1x+1⋅x+11dx=−∫t⋅(21⋅t3t3−1)⋅(t3−1)26t2dt
= − ∫ 3 t 3 − 1 d t = ∫ ( − 1 t − 1 + t + 2 t 2 + t + 1 ) d t \qquad\qquad =-\int \dfrac{3}{t^3-1}dt=\int(-\dfrac{1}{t-1}+\dfrac{t+2}{t^2+t+1})dt =−∫t3−13dt=∫(−t−11+t2+t+1t+2)dt
= − ln ∣ t − 1 ∣ + 1 2 ∣ t 2 + t + 1 ∣ + 3 arctan ( 2 t + 1 3 ) + C \qquad\qquad =-\ln|t-1|+\dfrac 12|t^2+t+1|+\sqrt 3\arctan(\dfrac{2t+1}{\sqrt 3})+C =−ln∣t−1∣+21∣t2+t+1∣+3arctan(32t+1)+C
= 1 2 ln t 3 − 1 ( t − 1 ) 3 + 3 arctan ( 2 t + 1 3 ) + C \qquad\qquad =\dfrac 12\ln\dfrac{t^3-1}{(t-1)^3}+\sqrt3\arctan(\dfrac{2t+1}{\sqrt 3})+C =21ln(t−1)3t3−1+3arctan(32t+1)+C
= 1 2 ln ∣ 2 x − 1 ( x + 1 x − 1 − 1 ) 3 ∣ + 3 arctan [ 2 3 x + 1 x − 1 3 + 1 3 ] + C \qquad\qquad =\dfrac 12\ln|\dfrac{\frac{2}{x-1}}{(\sqrt{\frac{x+1}{x-1}}-1)^3}|+\sqrt3\arctan[\dfrac{2}{\sqrt 3}\sqrt[3]{\dfrac{x+1}{x-1}}+\dfrac{1}{\sqrt 3}]+C =21ln∣(x−1x+1−1)3x−12∣+3arctan[323x−1x+1+31]+C
= − 1 2 ln ∣ x − 1 2 ∣ − 3 2 ln ∣ x + 1 x − 1 3 − 1 ∣ + 3 arctan [ 2 3 x + 1 x − 1 3 + 1 3 ] + C \qquad\qquad =-\dfrac12\ln|\dfrac{x-1}{2}|-\dfrac 32\ln|\sqrt[3]{\dfrac{x+1}{x-1}}-1|+\sqrt3\arctan[\dfrac{2}{\sqrt 3}\sqrt[3]{\dfrac{x+1}{x-1}}+\dfrac{1}{\sqrt 3}]+C =−21ln∣2x−1∣−23ln∣3x−1x+1−1∣+3arctan[323x−1x+1+31]+C
形如 R ( x , a x 2 + b x + c ) R(x,\sqrt{ax^2+bx+c}) R(x,ax2+bx+c)的积分
求形如 R ( x , a x 2 + b x + c ) R(x,\sqrt{ax^2+bx+c}) R(x,ax2+bx+c)的积分,其中 a ≠ 0 a\neq 0 a=0。
这个无理式可以化为以下三种形式:
- ∫ R ( x , ( x + p ) 2 + q 2 ) d x \int R(x,\sqrt{(x+p)^2+q^2})dx ∫R(x,(x+p)2+q2)dx
- ∫ R ( x , ( x + p ) 2 − q 2 ) d x \int R(x,\sqrt{(x+p)^2-q^2})dx ∫R(x,(x+p)2−q2)dx
- ∫ R ( x , q 2 − ( x + p ) 2 ) d x \int R(x,\sqrt{q^2-(x+p)^2})dx ∫R(x,q2−(x+p)2)dx
对这三种情况,可以由以下变换将它们化为三角有理式的积分:
- x + p = q tan t x+p=q\tan t x+p=qtant
- x + p = q sec t x+p=q\sec t x+p=qsect
- x + p = q sin t x+p=q\sin t x+p=qsint
例题
计算 ∫ x 2 − 2 x + 2 x − 1 d x \int \dfrac{\sqrt{x^2-2x+2}}{x-1}dx ∫x−1x2−2x+2dx
解:
\qquad 令 x − 1 = tan t x-1=\tan t x−1=tant,则 x 2 − 2 x + 2 = tan 2 t + 1 = 1 cos t \sqrt{x^2-2x+2}=\sqrt{\tan^2 t+1}=\dfrac{1}{\cos t} x2−2x+2=tan2t+1=cost1, 1 cos 2 t d t \dfrac{1}{\cos^2 t}dt cos2t1dt,于是
\qquad 原式 = 1 sin t ⋅ 1 cos 2 t d t = ∫ 1 ( cos 2 t − 1 ) cos 2 t ⋅ ( − sin t ) d t =\dfrac{1}{\sin t}\cdot\dfrac{1}{\cos^2t}dt=\int\dfrac{1}{(\cos^2t-1)\cos^2 t}\cdot(-\sin t)dt =sint1⋅cos2t1dt=∫(cos2t−1)cos2t1⋅(−sint)dt
= ∫ ( 1 cos 2 t − 1 − 1 cos 2 t ) d ( cos t ) = 1 2 ln ∣ cos t − 1 cos t + 1 ∣ + 1 cos t + C \qquad\qquad =\int(\dfrac{1}{\cos^2 t-1}-\dfrac{1}{\cos^2 t})d(\cos t)=\dfrac 12\ln|\dfrac{\cos t-1}{\cos t+1}|+\dfrac{1}{\cos t}+C =∫(cos2t−11−cos2t1)d(cost)=21ln∣cost+1cost−1∣+cost1+C
= 1 2 ln ∣ ( cos t − 1 ) 2 cos t 2 − 1 ∣ + x 2 − 2 x + 2 + C = 1 2 ln ( 1 − cos t sin t ) 2 + x 2 − 2 x + 2 + C \qquad\qquad =\dfrac 12\ln|\dfrac{(\cos t-1)^2}{\cos t^2-1}|+\sqrt{x^2-2x+2}+C=\dfrac 12\ln(\dfrac{1-\cos t}{\sin t})^2+\sqrt{x^2-2x+2}+C =21ln∣cost2−1(cost−1)2∣+x2−2x+2+C=21ln(sint1−cost)2+x2−2x+2+C
= ln ∣ 1 cos t − 1 tan x ∣ + x 2 − 2 x + 2 + C = ln ∣ x 2 − 2 x + 2 − 1 x − 1 ∣ + x 2 − 2 x + 2 + C \qquad\qquad =\ln|\dfrac{\frac{1}{\cos t}-1}{\tan x}|+\sqrt{x^2-2x+2}+C=\ln|\dfrac{\sqrt{x^2-2x+2}-1}{x-1}|+\sqrt{x^2-2x+2}+C =ln∣tanxcost1−1∣+x2−2x+2+C=ln∣x−1x2−2x+2−1∣+x2−2x+2+C
总结
对于这些简单的无理函数的不定积分,要善于换元,将无理函数的不定积分转化为有理函数的不定积分,然后运用之前的知识来求解即可。
相关文章:

简单的无理函数的不定积分
前置知识: 直接积分法有理函数的不定积分 简单的无理函数的不定积分 对无理函数积分的基本方法就是通过换元将其化为有理函数的积分。下面讲讲几类无理函数积分的求法。 注: R ( u , v ) R(u,v) R(u,v)是由 u , v u,v u,v与常数经过有限次四则运算得…...

《国际联网安全保护管理办法》
1.基本信息 (1997年12月11日国务院批准 1997年12月16日公安部令第33号发布 根据2011年1月8日《国务院关于废止和修改部分行政法规的决定》修订) 2.办法内容 第一章 总 则 第一条为了加强对计算机信息网络国际联网的安全保护,维护公共…...

Redis常用命令
目录 一. 字符串string常用操作命令 二. 哈希hash常用操作命令 三. 列表list常用操作命令 四. 集合set常用操作命令 五. 有序集合sorted set常用操作命令 六. 通用命令 一. 字符串string常用操作命令 SET key value 设置指定key的值GET key 获取指定key的值 SETEX key…...

功能齐全的 DIY ESP32 智能手表设计之原理图讲解二
相关设计资料下载ESP32 智能手表带心率、指南针设计资料(包含Arduino源码+原理图+Gerber+3D文件).zip 目录 构建 ESP32 智能手表所需的组件 光照度传感器电路讲解...

烦恼的高考志愿
烦恼的高考志愿 题目背景 计算机竞赛小组的神牛 V 神终于结束了高考,然而作为班长的他还不能闲下来,班主任老 t 给了他一个艰巨的任务:帮同学找出最合理的大学填报方案。可是 v 神太忙了,身后还有一群小姑娘等着和他约会&#x…...

【地铁上的设计模式】--结构型模式:适配器模式
前面几篇文章我们学习了创建型模式,从本篇文章开始,我们将学习结构型模式。 什么是结构型模式 结构型模式是一种设计模式,它描述了如何将类或对象结合在一起形成更大的结构,以提供新的功能或实现更复杂的行为。结构型模式包括以…...
重大剧透:你不用ChatGPT,它砸你饭碗
早晨看到路透社报道,盖茨说,与其争论技术的未来,不如专注于如何更好地利用人工智能。 这可能是他对马斯克他们呼吁暂停AI研发6个月的一种回应吧。 有种古语说:天下大势,浩浩汤汤,顺之者昌,逆之者…...

状态机模式
状态模式 状态模式定义:使用场景角色定义1. State一抽象状态角色2. ConcreteState一-具体状态角色3. Context--环境角色 需求背景1. 订单状态抽象类2. 定义订单具体状态类并集成基类(抽象类)2.1 订单创建状态2.2 订单已支付状态2.3 订单已发货状态2.4 订…...
瑞吉外卖:后台系统登录功能
文章目录 需求分析代码开发创建实体类导入返回结果类Rcontroller、service与mapperlogin.html 需求分析 点击登录按钮后,浏览器以POST方式向employee/login提交username和password,服务器经过处理后向浏览器返回某种格式的数据,其中包含&…...
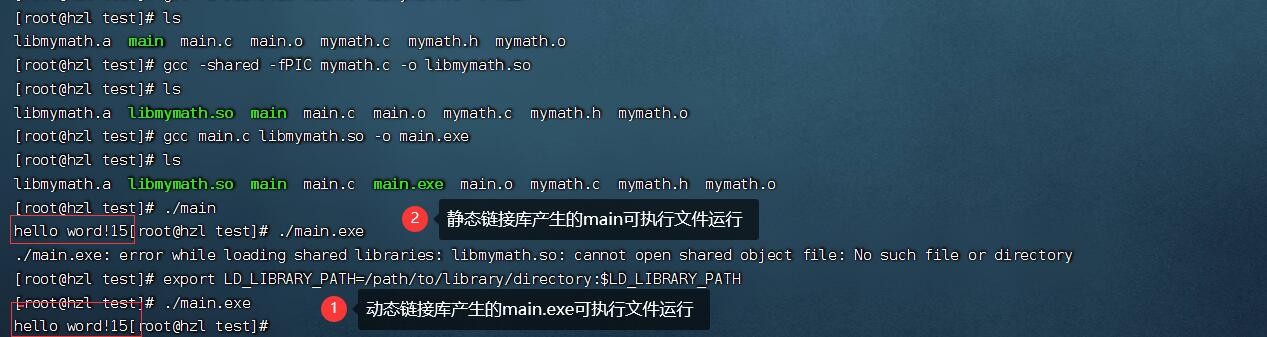
Linux拓展:链接库
一.说明 本篇博客介绍Linux操作系统下的链接库相关知识,由于相关概念已在Windows下链接库一文中介绍,本篇博客直接上操作。 二.静态链接库的创建和使用 1.提前看 这里主要介绍的是C语言的链接库技术,而在Linux下实现C语言程序,…...

基于.Net开发的、支持多平台、多语言餐厅点餐系统
今天给大家推荐一套支持多平台、多语言版本的订单系统,适合餐厅、酒店等场景。 项目简介 这是基于.Net Framework开发的,支持手机、平板、PC等平台、多语言版本开源的点餐系统,非常适合餐厅、便利店、超市、酒店等,该系统基础功…...

Windows系统SSL/TLS安全协议介绍
支持安全加密的https底层使用的就是SSL/TLS,在发起https请求之前需要先建立TCP连接,之后再进行SSL/TLS协议协商,协商通过后才能发起https请求。本文将详细介绍SSL/TLS协议相关的内容。 之前在项目中就出现过客户端SSL/TLS版本过低,导致向服务器发起连接时被服务器拒绝的问题…...
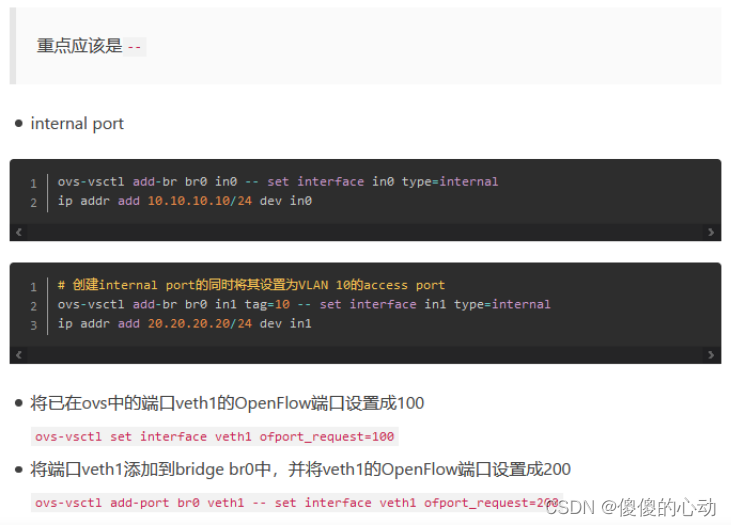
ovs-vsctl 命令详解
ovs-vsctl 命令详解 网桥Bridge 创建 Bridge ovs-vsctl add-br br0 删除 Bridge ovs-vsctl del-br br0 列出 Bridge ovs-vsctl list-br 显示详情 ovs-vsctl show 端口 Port 添加端口 ovs-vsctl add-port br0 p1 其中br0 为上面添加的bridge p1可以是物理端口或者vN…...

具备“记忆”功能的VBA目录选择器
大家使用任意一款浏览器(例如:Chrome、Edge)下载文件时,如果【另存为】对话框选择C:\Download,那么下次再次使用【另存为】功能,对话框默认显示C:\Download,而不是根目录。 在VBA开发中调用目录…...
electron入门 | 手把手带electron项目初始化
Electron是一个基于Chromium和 Node.js,可以使用 HTML、CSS和JavaScript构建跨平台应用的技术框架,兼容 Mac、Windows 和 Linux。 目录 1.了解electron 2.开发环境 3.初始化 采坑插曲: 1.了解electron Electron 可以让你使用纯 JavaScrip…...

力扣解法汇总2423. 删除字符使频率相同
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 给你一个下标从 0 开始的字符串 word ,字符串只包含小写英文字母。你…...

【超算/先进计算学习】日报8
目录 今日已完成任务列表遇到的问题及解决方案任务完成详细笔记阶段一阶段二阶段三阶段四 对自己的表现是否满意简述下次计划其他反馈 今日已完成任务列表 超算/高性能计算总结 遇到的问题及解决方案 无 任务完成详细笔记 阶段一 在学习的第一阶段,我们首先对需要…...
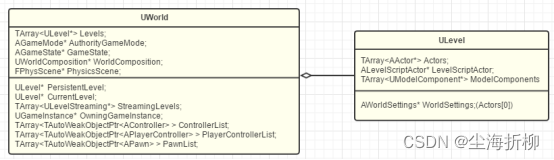
《LearnUE——基础指南:上篇—2》——GamePlay架构之Level和World
目录 听说世界是由多个Level组成的 1.2.1 引言 1.2.2 建造大陆(ULevel) 1.2.3构建世界(World) 1.2.4总结 听说世界是由多个Level组成的 1.2.1 引言 上小节谈到Actor和Component的关系,UE利用Actor的概念组成了世…...
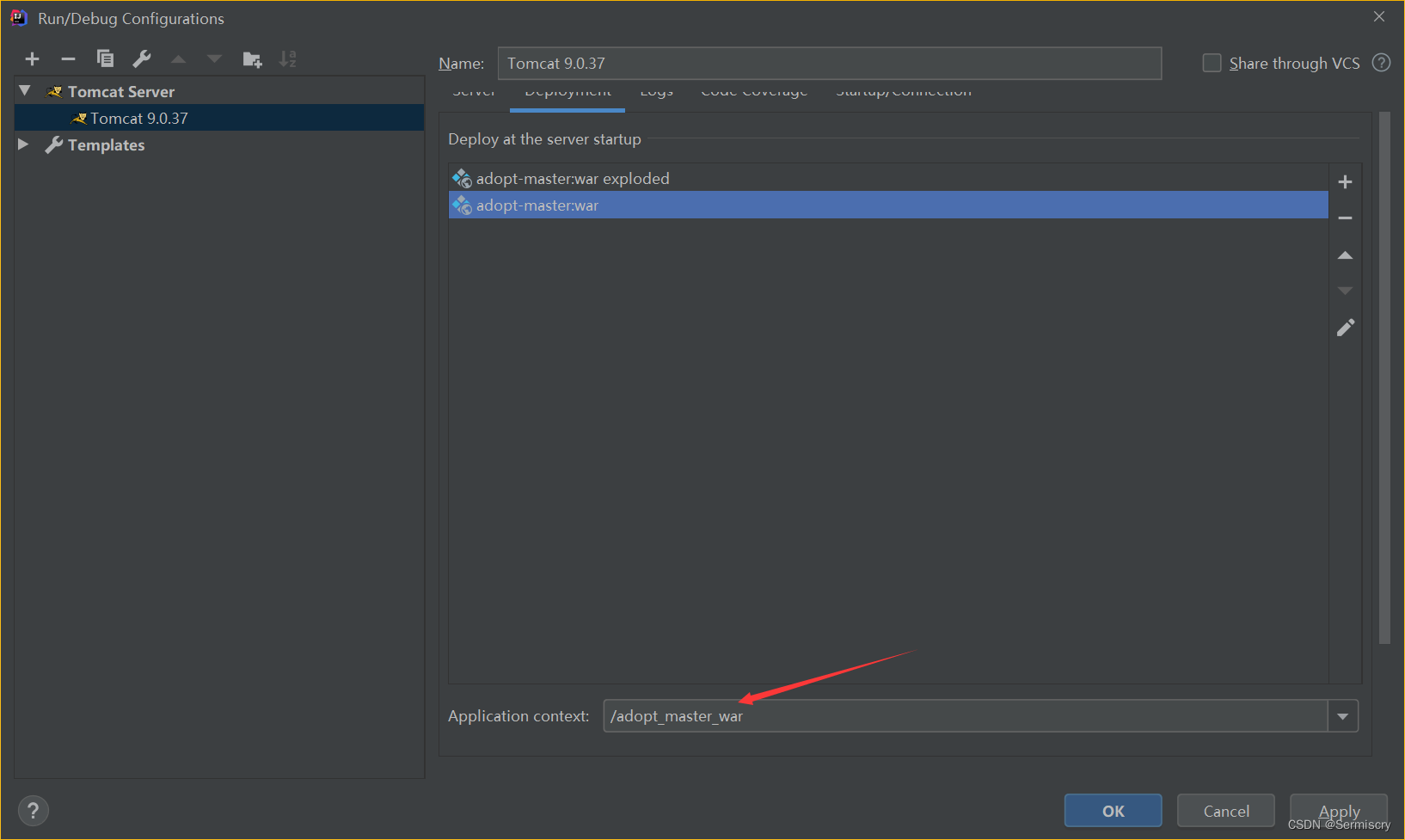
IDEA部署tomcat项目
文章目录 只是部署一下看到这里即可war和war exploded的区别warwar exploded update的动作update resourcesupdate classes and resourcesredeployrestart server 解决了拿到了一个tomcat项目后如何将它部署到IDEA里面的问题。 file->open 选中pom.xml并open as project …...

IAM角色
Identity-based policy,它关联到特定的User/Role/Group上,指定这些主体能对哪些资源进行怎样的操作 Resource-based policy,它关联到具体的AWS资源上,指定哪些主体可以对这个资源做怎样的操作 aws受信任关系视为aws服务可以实现&a…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
