机器学习小结之KNN算法
文章目录
- 前言
- 一、概念
- 1.1 机器学习基本概念
- 1.2 k 值
- 1.3 距离度量
- 1.4 加权方式
- 二、实现
- 2.1 手写实现
- 2.2 调库 Scikit-learn
- 2.3 测试自己的数据
- 三、总结
- 3.1 分析
- 3.2 KNN 优缺点
- 参考
前言
KNN (K-Nearest Neighbor)算法是一种最简单,也是一个很实用的机器学习的算法,在《机器学习实战》这本书中属于第一个介绍的算法。它属于基于实例的有监督学习算法,本身不需要进行训练,不会得到一个概括数据特征的模型,只需要选择合适的参数 K 就可以进行应用。KNN的目标是在训练数据中发现最佳的 K 个近邻,并根据这些近邻的标签来预测新数据的标签。每次使用 KNN 进行预测时,所有的训练数据都会参与计算。
kNN有很多应用场景:
- 分类问题,同时天然可以处理多分类问题,比如根据音乐的特征,将其归类到不同的类型。
- 推荐系统,根据用户的历史行为,推荐相似的物品或服务
- 图像识别,比如人脸识别、车牌识别等
一、概念
1.1 机器学习基本概念
机器学习是人工智能领域中非常重要的一个分支,它可以帮助我们从大量数据中发现规律并做出预测。
机器学习可以分为监督学习、无监督学习和半监督学习三种类型。
- 监督学习是指在训练数据中已经标注了正确答案,通过这些数据来训练模型,然后对新数据进行预测。
- 无监督学习是指在训练数据中没有标注正确答案,通过对数据的聚类、降维等操作来发现数据中的规律。
- 半监督学习则是介于有监督学习和无监督学习之间的一种方法。
下表是对机器学习一些基本概念解释
| 概念 | 解释 | 备注 |
|---|---|---|
| 分类 | 将数据集分为不同的类别 | 属于监督学习 |
| 聚类 | 将数据集分为由类似的对象组成多个类的过程 | 属于无监督学习 |
| 回归 | 指预测连续型数值数据 | 属于监督学习 |
| 样本集 | 一般指用于训练模型的数据集,一般分为训练集和测试集。 | 在样本集中,每个样本都包含一个或多个特征和一个标签。 |
| 特征 | 用于描述样本的属性或特点 | 通常是训练样本集的列,他们是独立测量的结果,多个特征联系在一起共同组成一个训练样本 |
| 标签 | 样本所属的类别或结果 | |
| 模型 | 从训练数据中学习到的规律或模式。 | 在机器学习中,模型可以用于预测新数据的标签或值 |
| 梯度 | 指函数在某一点处的变化率。 | 在机器学习中,梯度可以用于以最小化损失函数优化模型参数 |
1.2 k 值
k值是指在多个邻居中,选择前k个最相似邻居的类别来决定当前样本的类别,通常 k 是不大于20的整数,常选择3或5
1.3 距离度量
距离度量是指在 kNN 算法中用来计算样本之间距离的方法。常用的距离度量有欧氏距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离等。
-
欧式距离
-
二维平面
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} d=(x1−x2)2+(y1−y2)2
-
n维
d = ∑ i = 1 n ∣ x i − y i ∣ 2 d=\sqrt{\sum_{i=1}^{n}{\left| x_{i}-y_{i} \right|^{2}}} d=∑i=1n∣xi−yi∣2
-
-
曼哈顿距离
d = ∑ i = 1 n ∣ x i − y i ∣ d= \sum_{i=1}^{n}|x_i - y_i| d=∑i=1n∣xi−yi∣
-
切比雪夫距离
d = m a x ( ∣ x 1 − x 2 ∣ , ∣ y 1 − y 2 ∣ , ⋯ , ∣ x i − y i ∣ ) d= max(|x_1 - x_2|, |y_1 - y_2|, \cdots, |x_i - y_i|) d=max(∣x1−x2∣,∣y1−y2∣,⋯,∣xi−yi∣)
-
闵可夫斯基距离
d = ∑ i = 1 n ( ∣ x i − y i ∣ ) p p d = \sqrt[p]{\sum_{i=1}^{n}(|x_i - y_i|)^p} d=p∑i=1n(∣xi−yi∣)p
1.4 加权方式
KNN 算法中的加权方式指的是在计算距离时,对不同距离的样本使用不同的权重。这些权重可以是距离样本数据源的距离,也可以是不同样本之间的距离。加权的方式可以根据实际情况进行选择,以达到更好的分类或预测效果。
常用的数值数据加权方式如下:
- 加权平均值:将K个邻居的属性值加权平均后作为新数据点的预测值。
- 均值法:将K个邻居的属性值取平均值后作为新数据点的预测值。
- 最差值:将K个邻居的属性值取最小值和最大值,再取平均值作为新数据点的预测值。
常见的离散型数据加权方式如下:
- 反函数
- 高斯函数
- 多项式函数
不同的加权方式可以根据实际情况选择,以达到更好的分类或预测效果。
二、实现
手写数字数据集 为 《机器学习实战》第二章 提供的数据集:https://github.com/pbharrin/machinelearninginaction
2.1 手写实现
import numpy as np
from collections import Counter
import operator
import math
from os import listdir# inX 输入向量
# dataSet 训练集
# labels 训练集所代表的标签
# k 最近邻居数目
# output: label
def classify0(inX, dataSet, labels, k):sortedDistIndicies=euclideanDistance(inX, dataSet)classCount = {}for i in range(k):voteIlabel = labels[sortedDistIndicies[i]]classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1.0 * weight(sortedDistIndicies[i])sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)return sortedClassCount[0][0]def euclideanDistance(inX, dataSet):dataSetSize = dataSet.shape[0]diffMat = np.tile(inX, (dataSetSize, 1)) - dataSetsqDiffMat = diffMat ** 2sqDistances = sqDiffMat.sum(axis = 1)distances = sqDistances ** 0.5sortedDistIndicies = distances.argsort()return sortedDistIndiciesdef weight(dist):return 1def classify1(test, train, trainLabel, k):distances = []for i in range(len(train)):distance = np.sqrt(np.sum(np.square(test - train[i, :])))distances.append([distance, i])distances = sorted(distances)targets = [trainLabel[distances[i][1]] for i in range(k)]return Counter(targets).most_common(1)[0][0]def img2vector(filename):returnVect = np.zeros((1,1024))fr = open(filename)for i in range(32):lineStr = fr.readline()for j in range(32):returnVect[0,32*i+j] = int(lineStr[j])return returnVectdef handWritingDataSet(inputDir):hwLabels = []fileNames = []dataFileList = listdir(inputDir) m = len(dataFileList)dataMat = np.zeros((m,1024))for i in range(m):fileNameStr = dataFileList[i]fileStr = fileNameStr.split('.')[0] classNumStr = int(fileStr.split('_')[0])hwLabels.append(classNumStr)fileNames.append(fileStr)dataMat[i,:] = img2vector( inputDir + '/%s' % fileNameStr)return dataMat,hwLabels,fileNamestrainMat, trainLabels, _ = handWritingDataSet('digits/trainingDigits/')
testMat, testLabels,testFileNames = handWritingDataSet('digits/testDigits/')errorCount = 0
k = 3
for idx, testData in enumerate(testMat):prefictLabel = classify0(testData, trainMat, trainLabels, k)# prefictLabel = classify1(testData, trainMat, trainLabels, k)if testLabels[idx] != prefictLabel:errorCount+=1print("错误数据:%s.txt, 预测数字:%d" % (testFileNames[idx], prefictLabel))
print("k值:%d, 错误数量:%d, 错误率:%.3f%%" %(k, errorCount, errorCount / 1.0 / np.size(testMat, 0) * 100))

2.2 调库 Scikit-learn
文档地址:https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier
from sklearn.neighbors import KNeighborsClassifiertrainMat, trainLabels, _ = handWritingDataSet('digits/trainingDigits/')
testMat, testLabels,testFileNames = handWritingDataSet('digits/testDigits/')errorCount = 0
k = 3neigh = KNeighborsClassifier(n_neighbors=k)
neigh.fit(trainMat, trainLabels)for idx, testData in enumerate(testMat):prefictLabel = neigh.predict([testData])if testLabels[idx] != prefictLabel:errorCount+=1print("错误数据:%s.txt, 预测数字:%d" % (testFileNames[idx], prefictLabel))
print("k值:%d, 错误数量:%d, 错误率:%.3f%%" %(k, errorCount, errorCount / 1.0 / np.size(testMat, 0) * 100))

2.3 测试自己的数据
上面的手写数据集,训练集有1934个,测试集有946个,都是32x32的图片转的文本。如果想测试自己的手写数字,那就需要将手写数字图片先转成32x32像素格式的图片,然后再转成文本,下面是一个图片转文本代码
import cv2
import osdef img2txt(inputDir):dataFileList = os.listdir(inputDir)for file in dataFileList:if not file.endswith('png'):continueimg = cv2.imread(inputDir + file, cv2.IMREAD_GRAYSCALE)fr = open(inputDir + file.split('.')[0] + '.txt', 'w')height, width = img.shape[0:2]for row in range(height):line = ''for col in range(width):if img[row, col] > 250:line+='0'else:line+='1'fr.write(line)fr.write('\n')fr.close()
if __name__ == '__main__':img2txt('img/')
下面准备自己手写的0-9 十个数字进行测试,下面数字是用windows画图工具,先裁剪为32x32像素,再用鼠标手写实现。

将10个数字转成文本进行测试,结果错误率在30%

三、总结
3.1 分析
- 识别测试集手写数字时,总是有一些样本不能正确识别,通过观察发现是因为与其他类别特征比较接近
- 使用自身手写数字识别,识别错误的样本并不是因为相类似,例如4被识别为7,这个不太明白,可能与样本特征有关
3.2 KNN 优缺点
- 优点
- 思想简单,理论成熟,既可以用来做分类也可以用来做回归
- 由于选择距离最近的 k 个,对异常值不敏感
- 缺点
- KNN 需要计算每个测试样本与所有训练样本之间的距离,时间复杂度很高,计算成本也很高
- 无法给出数据任何的基础结构信息
- 算法比较简单,当训练数据较小时,对于一些很相似的不同类数据很难区分
参考
- https://github.com/pbharrin/machinelearninginaction
相关文章:

机器学习小结之KNN算法
文章目录 前言一、概念1.1 机器学习基本概念1.2 k 值1.3 距离度量1.4 加权方式 二、实现2.1 手写实现2.2 调库 Scikit-learn2.3 测试自己的数据 三、总结3.1 分析3.2 KNN 优缺点 参考 前言 KNN (K-Nearest Neighbor)算法是一种最简单,也是一个很实用的机器学习的…...

函函函函函函函函函函函数——two
🤩本文作者:大家好,我是paperjie,感谢你阅读本文,欢迎一建三连哦。 🥰内容专栏:这里是《C知识系统分享》专栏,笔者用重金(时间和精力)打造,基础知识一网打尽,…...
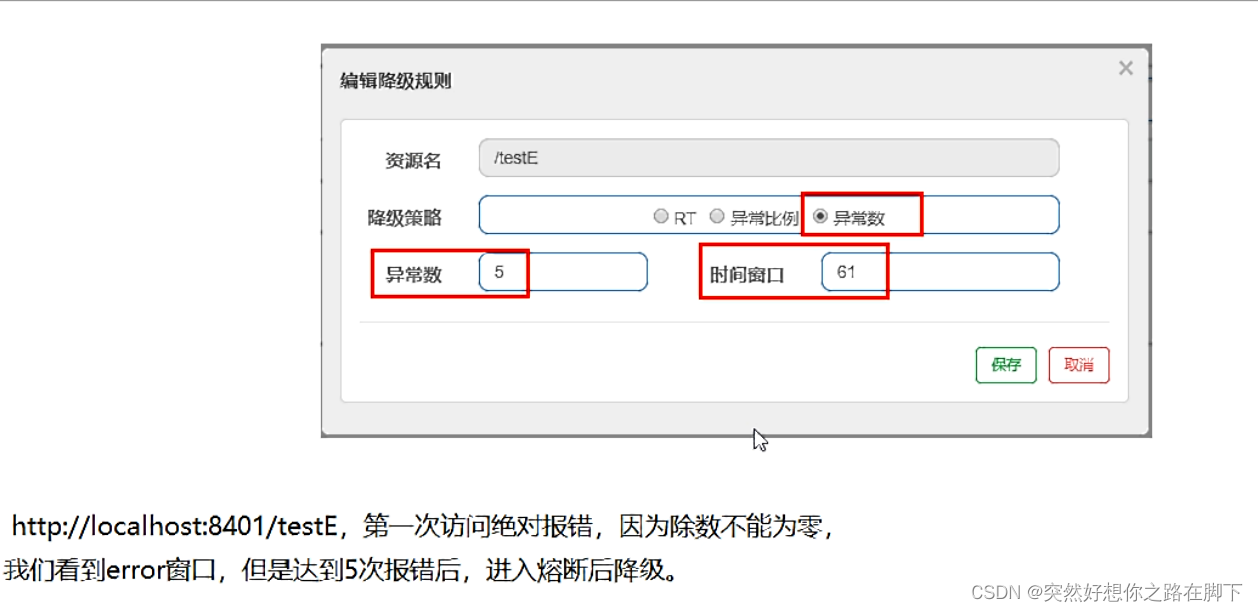
SpringCloud学习笔记06
九十五、Cloud Alibaba简介 0、why会出现SpringCloud alibaba Spring Cloud Netflix项目进入维护模式 1、是什么 官网:spring-cloud-alibaba/README-zh.md at 2.2.x alibaba/spring-cloud-alibaba GitHub 2、能干嘛 3、去哪下 spring-cloud-alibaba/README-…...
学系统集成项目管理工程师(中项)系列14_采购管理
1. 概念和术语 1.1. 采购是从项目团队外部获得产品、服务或成果的完整的购买过程 1.2. 三大类 1.2.1. 工程 1.2.2. 产品/货物 1.2.3. 服务 2. 主要过程 2.1. 编制采购管理计划 2.2. 实施采购 2.3. 控制采购 2.4. 结束采购 3. 合同 3.1. 包括买方和卖方之间的法律文…...

PMP课堂模拟题目及解析(第3期)
21. 一家农业设备制造商因一个缺陷部件而召回数千个产品。这个问题导致许多客户不满,公司花费 500 万美元来修理和更换零件。哪一种成本预算类型可以防止这个问题? A. 非一致性成本 B. 一致性成本 C. 矩阵图 D. 多标准决策分析 22. 一位团队成员…...
)
华为OD机试 - 微服务的集成测试( Python)
题目描述 现在有n个容器服务,服务的启动可能有一定的依赖性(有些服务启动没有依赖),其次服务自身启动加载会消耗一些时间。 给你一个 n x n 的二维矩阵useTime,其中 useTime[i][i]=10 表示服务i自身启动加载需要消耗10s useTime[i][j] = 1 表示服务i启动依赖服务j启动完…...
 — 企业面试汇总)
SLAM面试笔记(4) — 企业面试汇总
目录 1 大疆 一面(50min) 二面(30min) 三面(30min) 2 华为 一面(30min) 二面(30min) 三面(30min) 3 海康 一面(…...

五大新兴产业中,有三个中国出口全球占比居首-机器视觉工程师正处于需求旺盛阶段
五大新兴产业包含生物保健和电动汽车,新一代半导体、新一代显示器、二次电池。 在五大新兴产业中的三大领域——新一代半导体、新一代显示器、二次电池,中国对外出口在全球所占比重最高。 电动汽车,汽车行业一直对机器视觉工程师有着强烈的需求,无论比亚迪,特斯拉等等…...
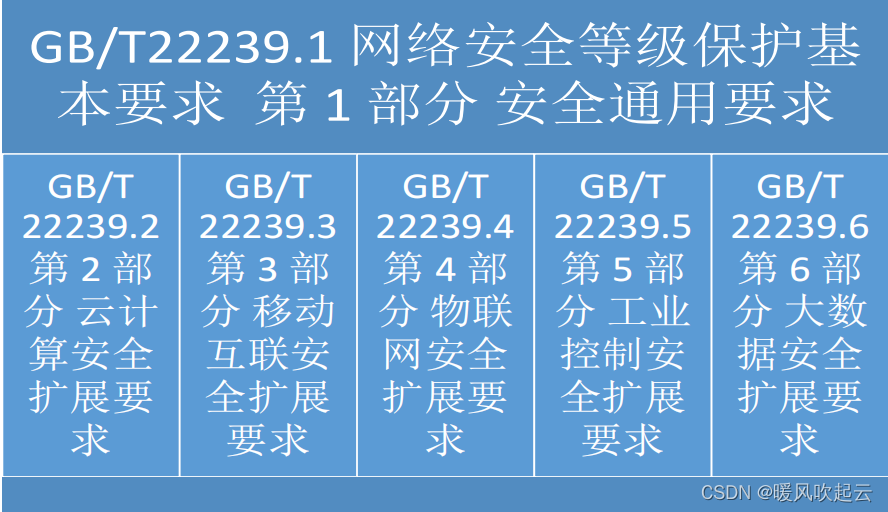
网络安全监管
网络安全监管 网络安全法律体系建设计算机犯罪、信息安全等基本概念我国立法体系及网络安全法我国的立法体系网络安全法出台背景基本概念安全法主要结构第一章 总则第二章 网络安全支持与促进第三章 网络运行安全第四章 网络信息安全第五章 监测预警与应急处置第六章 法律责任 …...
)
【code review】代码评审的18个军规(建议收藏)
文章目录 背景1. 添加必要的注释2.日志打印规范3. 命名规范4.参数校验5. 判空处理6. 异常处理规范7. 模块化,可扩展性8. 并发控制规范9. 单元测试规范10. 代码格式规范11. 接口兼容性12. 程序逻辑是否清晰,主次是否够分明13. 安全规范14. 事务控制规范15. 幂等处理规…...
:对话框)
PyQt5桌面应用开发(5):对话框
本文目录 PyQt5桌面应用系列对话框QDialogQDialog的基本用法按钮组 QMessageBox综合展示的例子结论 PyQt5桌面应用系列 PyQt5桌面应用开发(1):需求分析 PyQt5桌面应用开发(2):事件循环 PyQt5桌面应用开发&a…...

整洁的代码
文章目录 为什么要写整洁的代码什么是整洁的代码可读性运行效率扩展性 怎么写整洁的代码注释&命名函数&类代码结构 为什么要写整洁的代码 为什么要写整洁的代码,回答这个问题之前,也许应该想想写糟糕的代码的原因 是想快点完成吗?还是要赶时间吗?有可能.或许你觉得…...
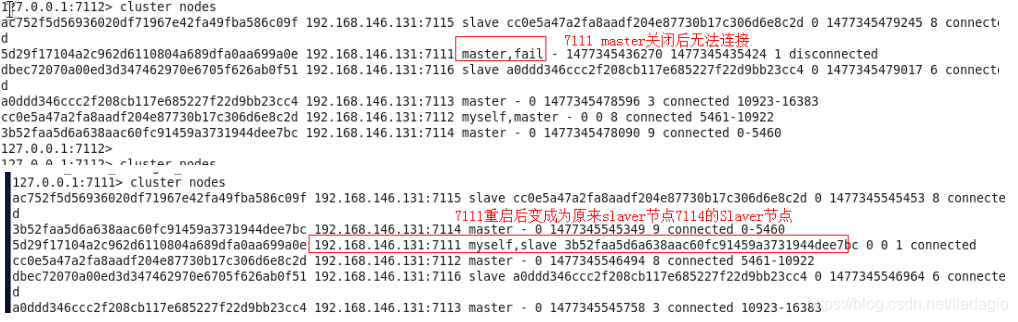
Redis集群常用命令及说明
一、集群的特点 1、集群架构特点 (1)所有的redis节点彼此互联(PING-PONG机制),内部使用二进制协议优化传输速度和带宽; (2)节点的fail是通过集群中超过半数的节点检测失效时才生效…...
使用edge浏览器,白嫖ChatGPT的保姆级教程来了
前言 嗨,大家好,我是希留,一个被迫致力于全栈开发的老菜鸟。 人工智能大浪潮已经来临,对于ChatGPT,我觉得任何一个玩互联网的人,都应该重视起来,用起来。但是国内使用需要解决科学上网、注册、…...

新人入职,都用这三招,让你安全度过试用期
刚入职工作 3招让你安全度过试用期 给新手小伙伴们分享几招 让你们能在试用期的时候平滑去度过 那么第一第一点就是 能自己解决的千万不要去问 千万不要去问 因为往往我们在去面试的时候 我们往往都是备足了很多的资料 备足了很多的面试题库 然后呢 你在给人家面试的时候总有一…...

小程序上车,车载小程序的信息安全是否可靠?
随着智能交通和车联网技术的快速发展,越来越多的车载应用程序(APP)进入人们的视野,从而推动了车载业务生态的不断发展。然而,车载应用程序的安全问题也引起了人们的广泛关注。为此,小程序容器技术作为一种有…...
)
华为OD机试 - 识图谱新词挖掘(Python)
题目描述 小华负责公司知识图谱产品,现在要通过新词挖掘完善知识图谱。 新词挖掘:给出一个待挖掘问题内容字符串Content和一个词的字符串word,找到content中所有word的新词。 新词:使用词word的字符排列形成的字符串。 请帮小华实现新词挖掘,返回发现的新词的数量。 …...

( 数组和矩阵) 378. 有序矩阵中第 K 小的元素 ——【Leetcode每日一题】
❓378. 有序矩阵中第 K 小的元素 难度:中等 给你一个 n x n n x n nxn 矩阵 m a t r i x matrix matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。 请注意,它是 排序后 的第 k 小元素,而不是第 …...
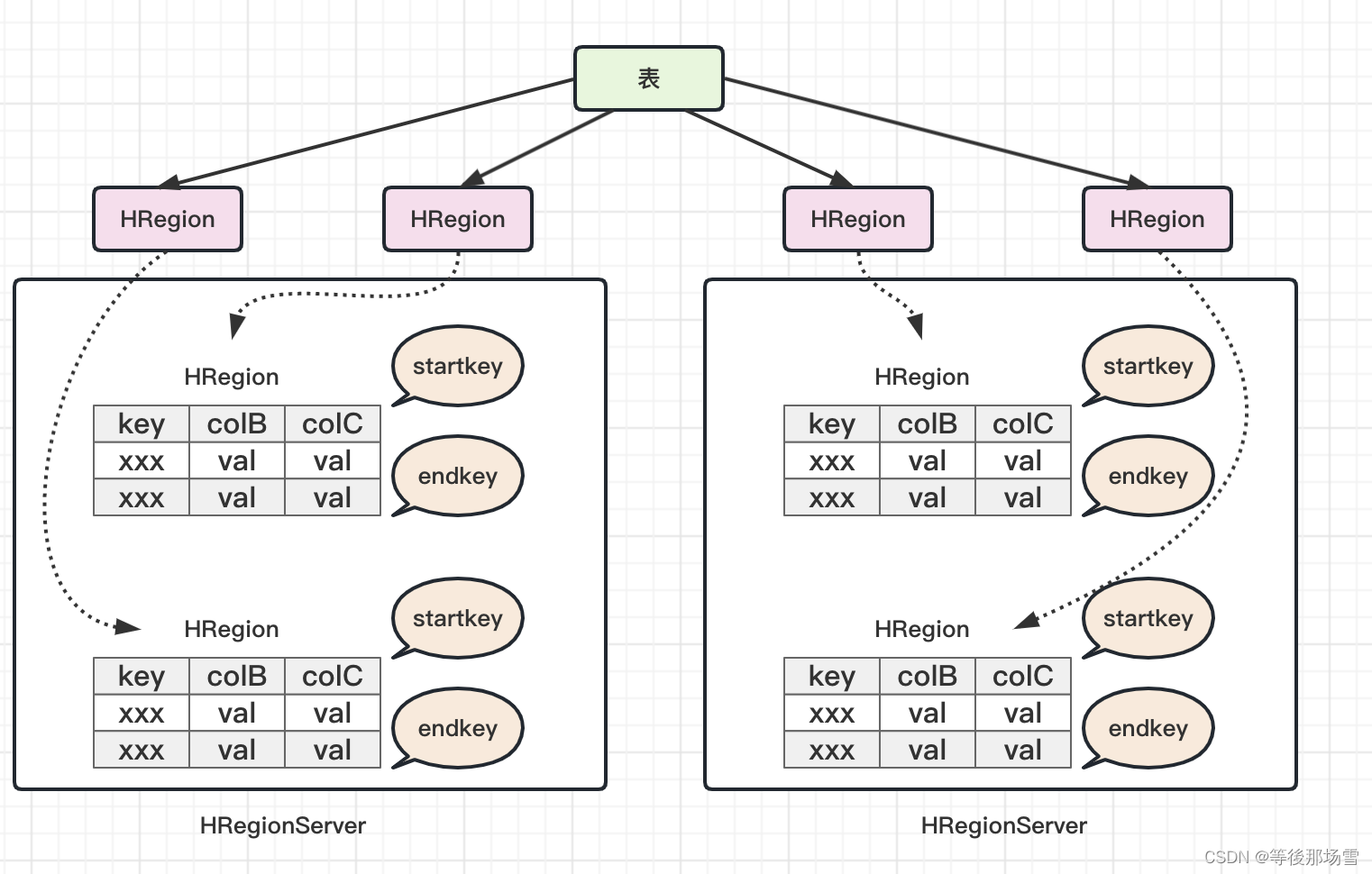
HBase架构篇 - Hadoop家族的天之骄子HBase
HBase的基本组成结构 表(table) HBase 的数据存储在表中。表名是一个字符串。表由行和列组成。 行(row) HBase 的行由行键(rowkey)和 n 个列(column)组成。行键没有数据类型&…...

STL及常用容器vector、list和deque的介绍
vector和built-in数组类似,它拥有一段连续的内存空间,并且起始地址不变,因此它能非常好的支持随机存取,即[]操作符,即可以以数组下标的方式来访问或遍历。但由于它的内存空间是连续的,所以在中间进行插入和删除会造成内存块的拷贝,另外,当该数组后的内存空间不够时,需…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
