( 数组和矩阵) 378. 有序矩阵中第 K 小的元素 ——【Leetcode每日一题】
❓378. 有序矩阵中第 K 小的元素
难度:中等
给你一个 n x n n x n nxn 矩阵 m a t r i x matrix matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
你必须找到一个内存复杂度优于 O ( n 2 ) O(n^2) O(n2) 的解决方案。
示例 1:
输入:matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出:13
解释:矩阵中的元素为 [1,5,9,10,11,12,13,13,15],第 8 小元素是 13
示例 2:
输入:matrix = [[-5]], k = 1
输出:-5
提示:
- n == matrix.length
- n == matrix[i].length
- 1 <= n <= 300
- − 1 0 9 < = m a t r i x [ i ] [ j ] < = 1 0 9 -10^9 <= matrix[i][j] <= 10^9 −109<=matrix[i][j]<=109
- 题目数据 保证 matrix 中的所有行和列都按 非递减顺序 排列
- 1 < = k < = n 2 1 <= k <= n^2 1<=k<=n2
进阶:
- 你能否用一个恒定的内存(即 O ( 1 ) O(1) O(1) 内存复杂度)来解决这个问题?
- 你能在 O ( n ) O(n) O(n) 的时间复杂度下解决这个问题吗?这个方法对于面试来说可能太超前了,但是你会发现阅读这篇文章(
this paper)很有趣。
💡思路:
法一:二分查找
找出二维矩阵中最小的数 l,最大的数 h,我们取中位数 mid = (l + h) / 2,在二维矩阵中寻找小于等于 mid 的元素个数cnt:
- 若这个
cnt小于k,表明第k小的数在右半部分且不包含mid,即l = mid + 1,h不变; - 若这个
cnt大于等于k,表明第k小的数在左半部分且可能包含mid,即l不变,h = mid - 1; - 当
l > h时,第k小的数即被找出,等于l。
法二:归并排序
由题目给出的性质可知,这个矩阵的每一行均为一个有序数组。问题即转化为从这 n 个有序数组中找第 k 大的数,可以想到利用归并排序的做法,归并到第 k 个数即可停止。
一般归并排序是两个数组归并,而本题是 n 个数组归并,所以需要用小根堆维护,以优化时间复杂度。
🍁代码:(Java、C++)
法一:二分查找
Java
class Solution {public int kthSmallest(int[][] matrix, int k) {int n = matrix.length;int l = matrix[0][0], h = matrix[n - 1][n - 1];while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int i = 0; i < n; i++){for(int j = 0; j < n && matrix[i][j] <= mid; j++){cnt++;}}if(cnt < k) l = mid + 1;else h = mid - 1;}return l;}
}
C++
class Solution {
public:int kthSmallest(vector<vector<int>>& matrix, int k) {int n = matrix.size();int l = matrix[0][0], h = matrix[n - 1][n - 1];while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int i = 0; i < n; i++){for(int j = 0; j < n && matrix[i][j] <= mid; j++){cnt++;}}if(cnt < k) l = mid + 1;else h = mid - 1;}return l;}
};
法二:归并排序
Java
class Solution {public int kthSmallest(int[][] matrix, int k) {PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {public int compare(int[] a, int[] b){return a[0] - b[0];}});int n = matrix.length;for(int i = 0; i < n; i++){//第一列分别为n数组的头结点pq.offer(new int[] {matrix[i][0], i, 0});}for(int i = 0; i < k - 1; i++){int[] now = pq.poll();//弹出最小的那个if(now[2] != n - 1){//不是一行的最后一个元素pq.offer(new int[]{matrix[now[1]][now[2] + 1], now[1], now[2] + 1});}}return pq.poll()[0];}
}
C++
class Solution {
public:int kthSmallest(vector<vector<int>>& matrix, int k) {struct point{int val, x, y;point(int val, int x, int y): val(val), x(x), y(y){};bool operator> (const point& a)const{return this->val > a.val;}};priority_queue<point, vector<point>, greater<point>> que;int n = matrix.size();for(int i = 0; i < n; i++){que.emplace(matrix[i][0], i, 0);}for(int i = 0; i < k - 1; i++){point now = que.top();que.pop();if(now.y != n - 1){que.emplace(matrix[now.x][now.y + 1], now.x, now.y + 1);}}return que.top().val;}
};
🚀 运行结果:

🕔 复杂度分析:
- 时间复杂度: O ( n l o g ( r − l ) ) O(nlog(r - l)) O(nlog(r−l)),二分查找进行次数为 O ( n l o g ( r − l ) ) O(nlog(r - l)) O(nlog(r−l)), 每次操作时间复杂度为 O ( n ) O(n) O(n)。归并排序时间复杂度为 O ( k l o g n ) O(klogn) O(klogn),归并
k次,每次堆中插入和弹出的操作时间复杂度均为 l o g n logn logn。 - 空间复杂度: O ( 1 ) O(1) O(1);归并排序空间复杂度为 O ( n ) O(n) O(n),堆的大小始终为
n。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 378. 有序矩阵中第 K 小的元素 ——【Leetcode每日一题】
❓378. 有序矩阵中第 K 小的元素 难度:中等 给你一个 n x n n x n nxn 矩阵 m a t r i x matrix matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。 请注意,它是 排序后 的第 k 小元素,而不是第 …...
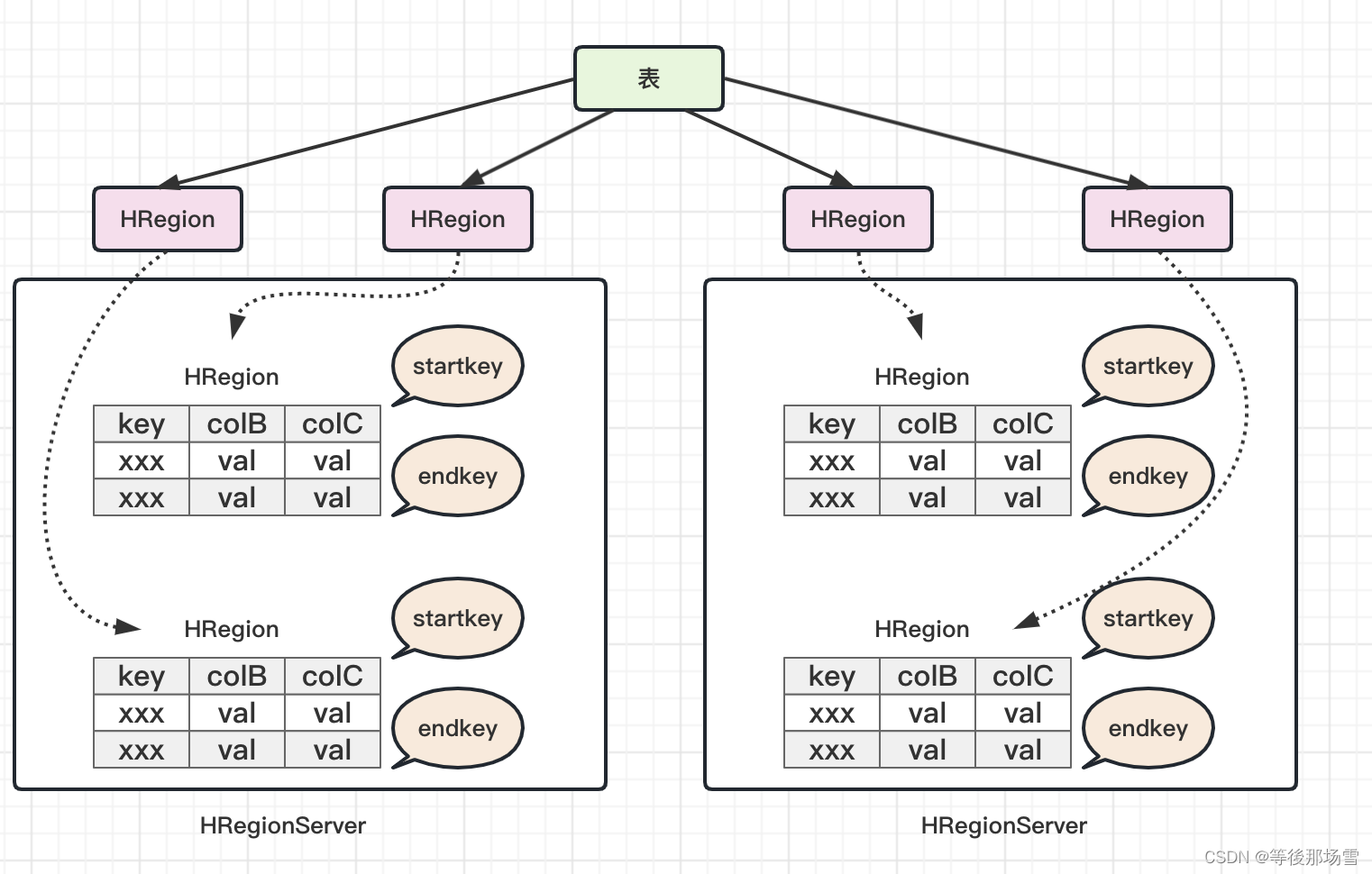
HBase架构篇 - Hadoop家族的天之骄子HBase
HBase的基本组成结构 表(table) HBase 的数据存储在表中。表名是一个字符串。表由行和列组成。 行(row) HBase 的行由行键(rowkey)和 n 个列(column)组成。行键没有数据类型&…...

STL及常用容器vector、list和deque的介绍
vector和built-in数组类似,它拥有一段连续的内存空间,并且起始地址不变,因此它能非常好的支持随机存取,即[]操作符,即可以以数组下标的方式来访问或遍历。但由于它的内存空间是连续的,所以在中间进行插入和删除会造成内存块的拷贝,另外,当该数组后的内存空间不够时,需…...

SpringBoot统一功能处理(统⼀⽤户登录权限验证、统⼀异常处理、统⼀数据格式封装)
统⼀⽤户登录权限验证 1、最初的用户登录效验:在每个方法里面获取session和 session 中的用户信息,如果存在用户,那么就认为登录成功了,否则就登录失败了。 2、第二版用户登录效验:提供了统一的方法,在每个需要验证的方法中调用…...
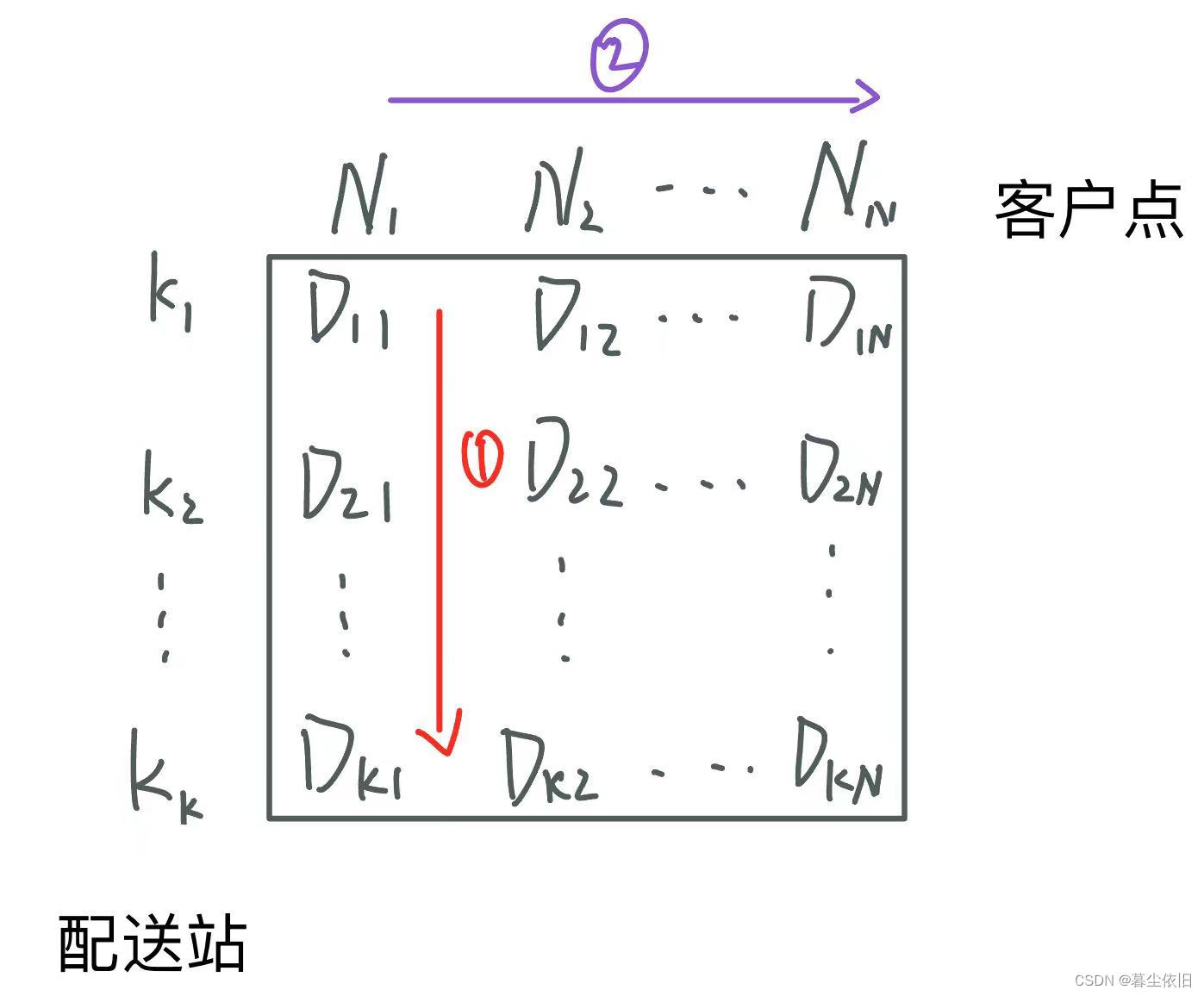
华为实习笔试复盘(1)配送站和客户问题
写在前面 自己玩了很多项目,但是最近准备秋招的过程中,发现自己对于算法和编程语言的基本功夫实在是太欠缺了。 投递了华为的实习岗位,4.26参加机考,一做题就发现了自己很多地方都不会。这里写下笔试后的复盘以警醒自己。 题目 …...

alibaba yalantingLibs struct_pack代码梳理
这里写目录标题 struct_pack 接口序列化序列化对象到新字节容器序列化对象到容器尾部将序列化结果保存到指针指向的内存中多参数序列化将序列化结果保存到输出流自定义类型序列化序列化到自定义的输出流 反序列化基本反序列化从指针指向的内存中反序列化反序列化到已有对象多参…...
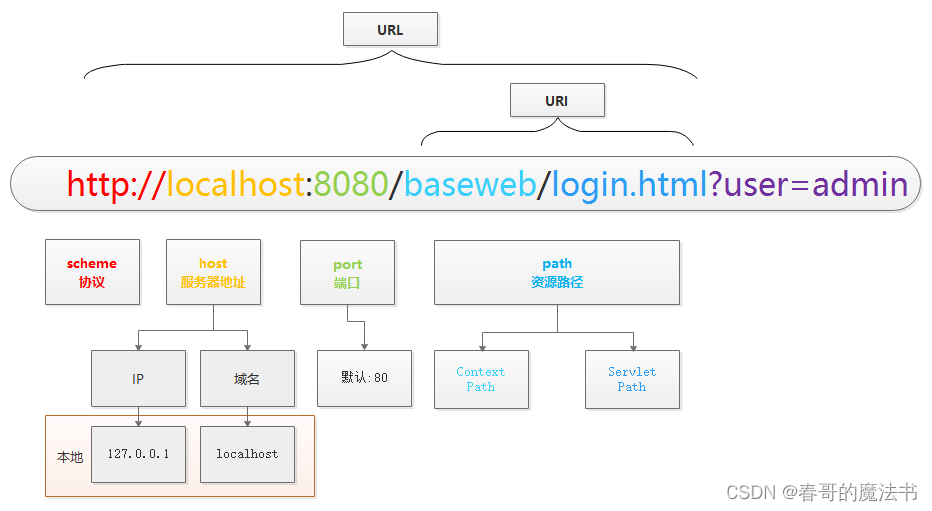
JavaWeb( 二 ) URL
1.4.URL统一资源定位符 URL代表Uniform Resource Locator 统一资源定位符,也叫 URL地址 。是用于标识和定位Web上资源的地址,通常用于在Web浏览器中访问网站和文件。 URL由若干部分组成,scheme:// host : port / path 例如: htt…...

Python斐波那契数列
斐波那契数列是一个经典的数学问题,在 Python 中可以使用多种方法来实现,下面是几个常见的实现方式: 1. 使用递归 python def fibonacci_recursive(n): if n < 1: return n else: return fibonacci_recursive(n…...
)
华为OD机试 - 模拟商场优惠打折(Python)
题目描述 模拟商场优惠打折,有三种优惠券可以用,满减券、打折券和无门槛券。 满减券:满100减10,满200减20,满300减30,满400减40,以此类推不限制使用; 打折券:固定折扣92折,且打折之后向下取整,每次购物只能用1次; 无门槛券:一张券减5元,没有使用限制。 每个人…...
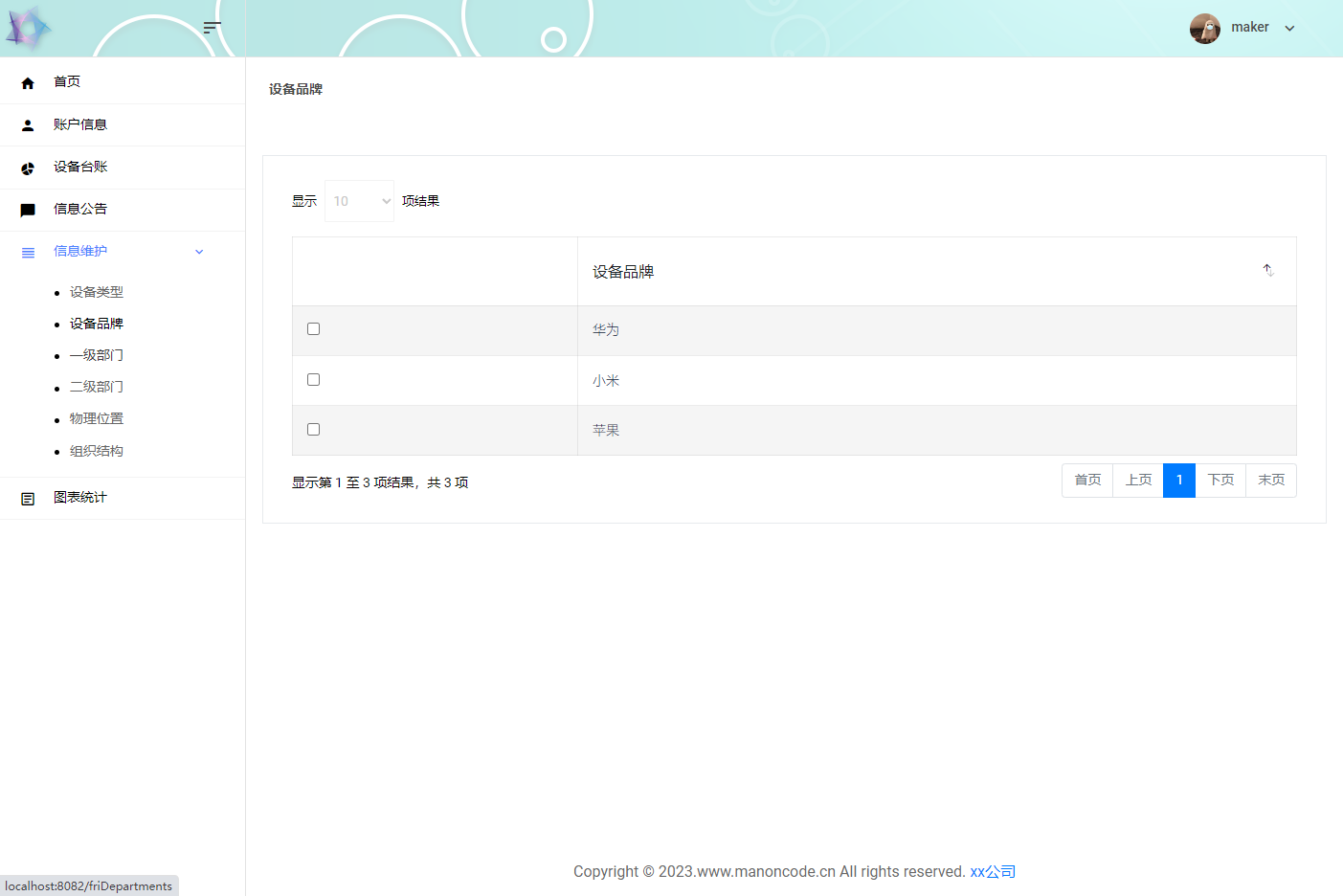
【JAVA程序设计】(C00132)基于SSM的固定资产管理系统
基于SSM的固定资产管理系统 项目简介项目获取开发环境项目技术运行截图 项目简介 本系统为基于SSM的固定资产管理系统,本系统分为二种用户:超级管理员和普通管理员; 超级管理员功能: 首页查看、设备管理、平台账户管理、设备台账…...

简单的无理函数的不定积分
前置知识: 直接积分法有理函数的不定积分 简单的无理函数的不定积分 对无理函数积分的基本方法就是通过换元将其化为有理函数的积分。下面讲讲几类无理函数积分的求法。 注: R ( u , v ) R(u,v) R(u,v)是由 u , v u,v u,v与常数经过有限次四则运算得…...

《国际联网安全保护管理办法》
1.基本信息 (1997年12月11日国务院批准 1997年12月16日公安部令第33号发布 根据2011年1月8日《国务院关于废止和修改部分行政法规的决定》修订) 2.办法内容 第一章 总 则 第一条为了加强对计算机信息网络国际联网的安全保护,维护公共…...

Redis常用命令
目录 一. 字符串string常用操作命令 二. 哈希hash常用操作命令 三. 列表list常用操作命令 四. 集合set常用操作命令 五. 有序集合sorted set常用操作命令 六. 通用命令 一. 字符串string常用操作命令 SET key value 设置指定key的值GET key 获取指定key的值 SETEX key…...

功能齐全的 DIY ESP32 智能手表设计之原理图讲解二
相关设计资料下载ESP32 智能手表带心率、指南针设计资料(包含Arduino源码+原理图+Gerber+3D文件).zip 目录 构建 ESP32 智能手表所需的组件 光照度传感器电路讲解...

烦恼的高考志愿
烦恼的高考志愿 题目背景 计算机竞赛小组的神牛 V 神终于结束了高考,然而作为班长的他还不能闲下来,班主任老 t 给了他一个艰巨的任务:帮同学找出最合理的大学填报方案。可是 v 神太忙了,身后还有一群小姑娘等着和他约会&#x…...

【地铁上的设计模式】--结构型模式:适配器模式
前面几篇文章我们学习了创建型模式,从本篇文章开始,我们将学习结构型模式。 什么是结构型模式 结构型模式是一种设计模式,它描述了如何将类或对象结合在一起形成更大的结构,以提供新的功能或实现更复杂的行为。结构型模式包括以…...
重大剧透:你不用ChatGPT,它砸你饭碗
早晨看到路透社报道,盖茨说,与其争论技术的未来,不如专注于如何更好地利用人工智能。 这可能是他对马斯克他们呼吁暂停AI研发6个月的一种回应吧。 有种古语说:天下大势,浩浩汤汤,顺之者昌,逆之者…...

状态机模式
状态模式 状态模式定义:使用场景角色定义1. State一抽象状态角色2. ConcreteState一-具体状态角色3. Context--环境角色 需求背景1. 订单状态抽象类2. 定义订单具体状态类并集成基类(抽象类)2.1 订单创建状态2.2 订单已支付状态2.3 订单已发货状态2.4 订…...
瑞吉外卖:后台系统登录功能
文章目录 需求分析代码开发创建实体类导入返回结果类Rcontroller、service与mapperlogin.html 需求分析 点击登录按钮后,浏览器以POST方式向employee/login提交username和password,服务器经过处理后向浏览器返回某种格式的数据,其中包含&…...
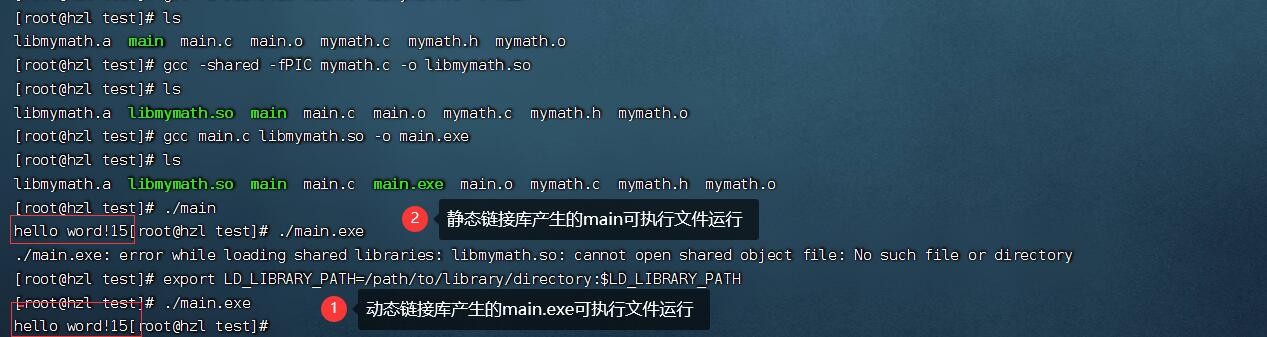
Linux拓展:链接库
一.说明 本篇博客介绍Linux操作系统下的链接库相关知识,由于相关概念已在Windows下链接库一文中介绍,本篇博客直接上操作。 二.静态链接库的创建和使用 1.提前看 这里主要介绍的是C语言的链接库技术,而在Linux下实现C语言程序,…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
