【蓝桥杯集训·每日一题】Acwing 3729. 改变数组元素
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 一维差分
- 区间合并
一、题目
1、原题链接
3729. 改变数组元素
2、题目描述
给定一个空数组 V 和一个整数数组
a1,a2,…,an。现在要对数组 V 进行 n 次操作。
第 i 次操作的具体流程如下:
从数组 V 尾部插入整数 0。 将位于数组 V 末尾的
ai个元素都变为 1(已经是 1 的不予理会)。
注意:
ai可能为 0,即不做任何改变。ai可能大于目前数组 V 所包含的元素个数,此时视为将数组内所有元素变为 1。请你输出所有操作完成后的数组 V。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含整数 n。
第二行包含 n 个整数 a1,a2,…,an。
输出格式
每组数据输出一行结果,表示所有操作完成后的数组 V,数组内元素之间用空格隔开。
数据范围
1≤T≤20000,1≤n≤2×105,0≤ai≤n,保证一个测试点内所有 n 的和不超过 2×105。
输入样例:
3 6 0 3 0 0 1 3 10 0 0 0 1 0 5 0 0 0 2 3 0 0 0输出样例:
1 1 0 1 1 1 0 1 1 1 1 1 0 0 1 1 0 0 0
二、解题报告
1、思路分析
思路1:差分+区间合并
(1)将每个需要+1的区间合并,得到若干个不重叠的区间。
(2)对每个区间利用差分将每个区间元素值+1。
(3)对差分数组求前缀和得到结果数组,输出即可。
思路2:y总思路
思路来源:y总每日一题b站视频链接
y总yyds
(1)直接对每个区间进行差分将每个区间元素值+1。
(2)对差分数组求前缀和得到数组,如果数组元素值>=1说明进行了+1操作,直接输出1;否则说明该值没有+1,直接输出0。
2、时间复杂度
思路1时间复杂度O(nlogn)(sort()函数、快排时间复杂度nlogn级别)
思路2时间复杂度O(n)
3、代码详解
思路1代码
#include <iostream>
#include <algorithm>
#include <utility>
#include <vector>
#include <cstring>
using namespace std;
typedef pair<int,int> PII;
vector<PII> v;
const int N=200010;
int pos;
int t,n;
int a[N],b[N];
//区间合并
void merge(vector<PII> &vec){vector<PII> ans;sort(vec.begin(),vec.end());int st=-1,ed=-1;for(auto i:vec){if(ed<i.first){if(st!=-1) ans.push_back({st,ed});st=i.first,ed=i.second;}else ed=max(ed,i.second); }if(st!=-1) ans.push_back({st,ed});vec=ans;
}
//差分
void insert(int l,int r,int c){b[l]+=c;b[r+1]-=c;
}
int main(){cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++){pos=i; //pos记录当前数组中元素的个数cin>>a[i];if(a[i]==0) continue; //如果需要将0个元素置为1,跳过下面步骤,执行下一次循环if(pos<=a[i]){ //如果需要置为1的元素个数超过数组元素个数v.push_back({1,pos}); //需置成1的区间为整个数组}else{v.push_back({pos-a[i]+1,pos}); //否则需置成1的区间为数组后a[i]个元素所在区间}}merge(v);for(auto i:v){insert(i.first,i.second,1);}//差分数组求前缀和,得到结果数组for(int i=1;i<=pos;i++){b[i]+=b[i-1];cout<<b[i]<<' ';}cout<<endl;memset(b,0,sizeof b); //注意不要忘记,下一次循环前需将元素置为0pos=0; //pos也别忘记v.clear(); //区间数组也得清空} return 0;
}
思路2代码
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=200010;
int t,n;
int a[N],b[N];
//差分
void insert(int l,int r,int c){b[l]+=c;b[r+1]-=c;
}
int main(){cin>>t;int pos=0;while(t--){cin>>n;for(int i=1;i<=n;i++){pos=i; //pos代表当前元素个数cin>>a[i];if(a[i]==0) continue; //如果需要把0个元素置为1,直接跳过下面步骤,执行下一次循环if(a[i]>=pos){ //如果需要置的元素个数大于等于区间元素数insert(1,pos,1); //将[1,pos]即整个区间加1}else{insert(pos-a[i]+1,pos,1); //否则只个数组后a[i]个元素加1}}//差分数组求前缀和,得到每个区间加1后的结果数组for(int i=1;i<=pos;i++){b[i]+=b[i-1];if(b[i]>=1) cout<<1<<' '; //如果某个位置加了大于等于1次个1,输出1else cout<<0<<' '; //如果没有加过1,输出0}cout<<endl;memset(b,0,sizeof b); //注意不要忘记,下一次循环前需将元素置为0pos=0; //pos也别忘记}return 0;
}
三、知识风暴
一维差分
- 一维差分可以快速地给指定区间的每个数加任意常数c
- 差分数组顾名思义就是相邻元素之差组成的数组。
- 我们如果要对某个区间加减任意常数c可以先求其差分数组,然后对差分数组进行操作。设b数组为差分数组。
操作:对[l,r]区间每个数+c:b[l]+=c,b[r+1]-=c。
最后再对差分数组求前缀和即为处理后的原数组。区间合并
- 区间合并就是将某些有重叠(或者说是相交)的区间合并。
- 基本思路:
- 将所有需要合并的区间按左端点排好序。
- 以排好序的第一个区间开始,看第二个区间是否与第一个区间有重叠,而且右端点比第一个区间大,如果满足则合并,合并操作就是将第一个区间的右端点更新成第二个区间的右端点;如果第二个区间被第一个区间所完全覆盖,则合并后的区间就是第一个区间,不需要操作;如果第二个区间和第一个区间完全没有交集,说明第二个区间的左端点比第一个区间的右端点大,而我们又是按照区间左端点进行排序的,则下一个区间的左端点也比第一个区间的左端点大,说明当前第一个区间已经和后面所有区间都不可能有交集了,所以第一个区间已经合并完成,我们将其放入结果数组中,下一次将剩下区间里的第一个区间进行如上合并操作,直到完成所有区间合并操作,将最后一个区间也放入结果数组,合并完成。
相关文章:

【蓝桥杯集训·每日一题】Acwing 3729. 改变数组元素
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一维差分区间合并一、题目 1、原题链接 3729. 改变数组元素 2、题目描述 给定一个空数组 V 和一个整数数组 a1,a2,…,an。 现在要对数组 V 进行 n 次操作。 第 i 次操作的…...
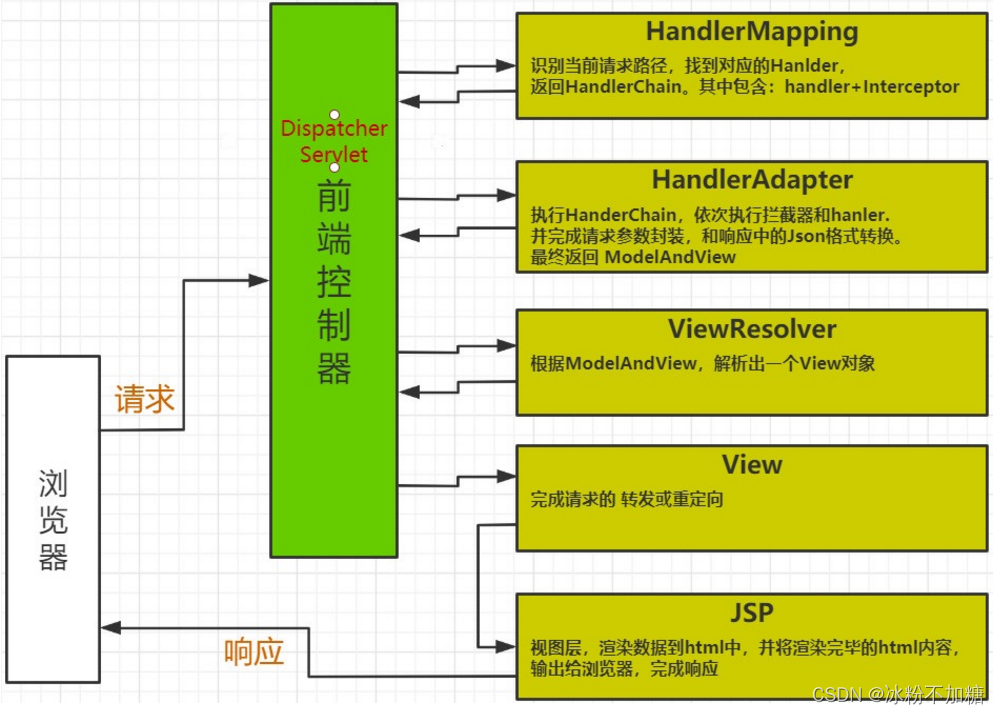
springmvc执行流程
文章目录前言一、springMVC请求执行流程二、组件说明以下组件通常使用框架提供实现:总结前言 本篇文章是对springmvc的补充 接上篇文章springmvc入门https://blog.csdn.net/l_zl2021/article/details/127120873 一、springMVC请求执行流程 1.用户发送请求至前端控制…...
SpringMVC(2)
一)接受到JSON格式的数据:使用RequestBody来进行接收 ResponseBody表示的是返回一个非页面的数据 RequestBody表示的是后端要接受JSON格式的数据 一)接收单个格式的JSON格式的数据,我们使用一个对象来进行接收 1)我们之前接受GET请求中的queryString中的参数的时候&…...

Jackson序列化json时null转成空串或空对象
在项目中可能会遇到需要将null转"",可以通过以下方法解决。一:添加JacksonConfig 配置import com.fasterxml.jackson.core.JsonGenerator;import com.fasterxml.jackson.databind.JsonSerializer;import com.fasterxml.jackson.databind.Objec…...

如何将Python的上级目录的文件导入?【from.import】
假如有如下目录: -python ----file1 ---------file1_1 ------------------pfile1_1.py ---------pfile1.py ----file2 ---------pfile2.py ----pfile.py ----data.py 在pfile1_1.py中想要将pfile.py 导入怎么办? 首先将其上级目录添加到系统目…...

Java实现碧蓝航线连续作战
目录一.实现功能二.主要思路三.代码实现四.用exe4j生成.exe程序五.最终效果六.代码开源一.实现功能 主线图作战结束到结算页自动点击再次前往 二.主要思路 判断是否进入了结算界面:记录结算界面某个像素点的RGB值,每隔3秒对这个像素点进行比对 移动鼠标…...
Docker笔记
文章目录1.docker为什么会出现2.docker是什么3.传统虚拟机和容器的对比3.1虚拟机3.2容器虚拟化技术3.3两者对比3.4为什么Docker会比VM虚拟机快?4.docker能干嘛6.docker的应用场景7.docker三要素一:镜像(Image)二:容器&…...
情人节使用AI TOOL来创建一个甜言蜜语的女伴
一、首先使用chatgpt生成一段情侣间的对话,需要反复几次,达到满意的程度,然后将女方的话归在一起。 这是一个情侣私下谈话的场景,女方表示对男朋友精心准备的情人节安排和礼物表示很满意 二、 打开网站:https://lexic…...
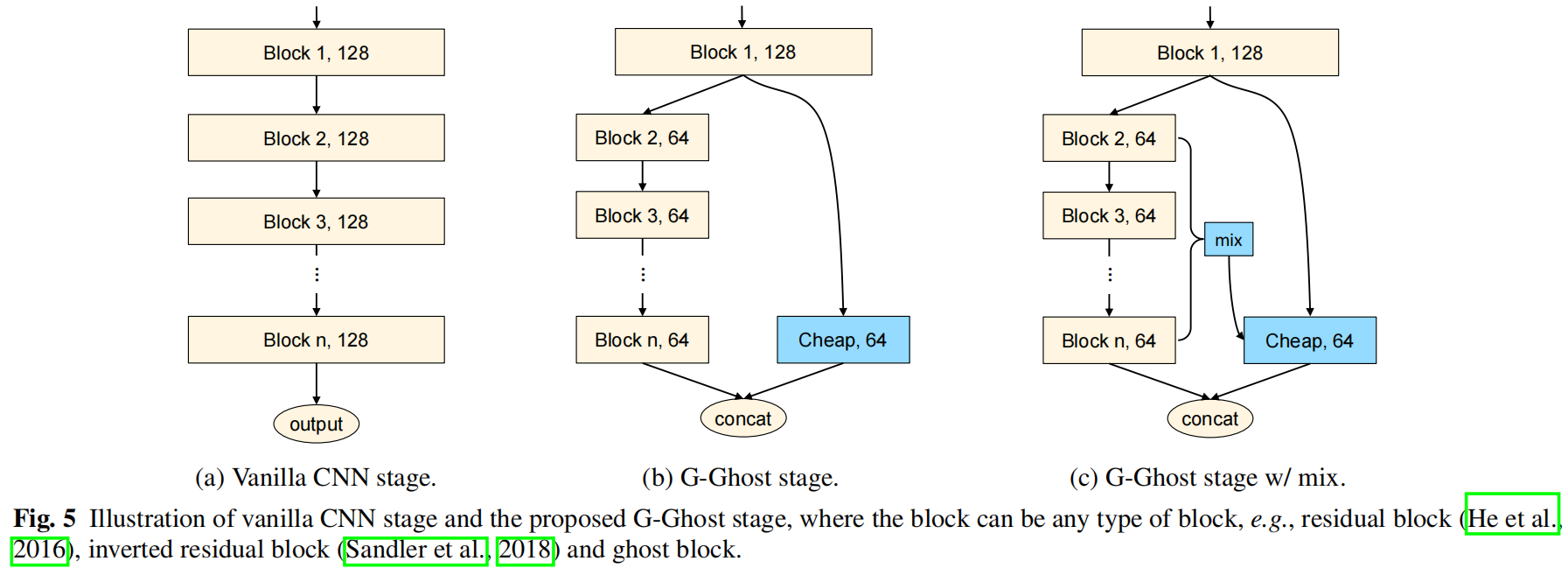
G-GhostNet(IJCV 2022)原理与代码解析
paper:GhostNets on Heterogeneous Devices via Cheap Operationscode:https://github.com/huawei-noah/Efficient-AI-Backbones/blob/master/g_ghost_pytorch/g_ghost_regnet.py前言本文提出了两种轻量网路,用于CPU端的C-GhostNet和用于GPU端…...
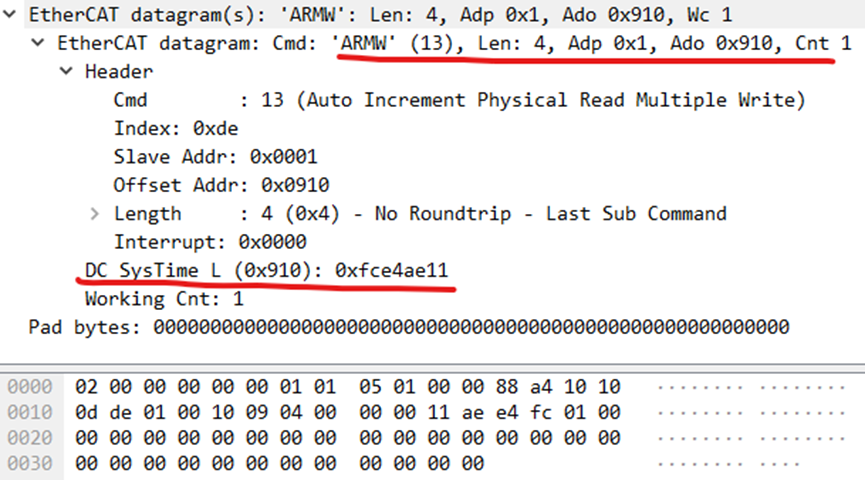
Ethercat系列(5)TWcat3激活过程的协议分析(续1)
顺序写系统时间偏移从-》主顺序写时间延迟主-》从从-》主顺序写分布式时钟启动主-》从从-》主读多重写系统时间主-》从从-》主顺序写应用层控制主-》从从-》主顺序读错误计数器主-》从从-》主顺序读应用层状态主-》从从-》主顺序读应用层,广播写错误计数器主-》从从…...
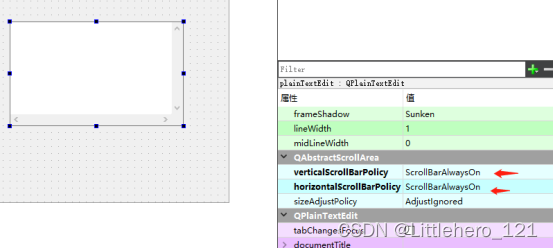
QT入门Input Widgets之QScrollBar
目录 一、界面布局功能 1、界面位置介绍 2、控件界面基本属性 2.1 horizontalScrollBar界面属性 3、样式设置 此文为作者原创,创作不易,转载请标明出处! 一、界面布局功能 1、界面位置介绍 QScrollBar主要分为两种,一种垂直…...
)
【ML】基于机器学习的心脏病预测研究(附代码和数据集,多层感知机模型)
写在前面: 首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大努力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 之前创作过心脏病预测研究文章如下: 【ML】基于机器学习的心脏病预测研究(附代码和数据集,逻辑回归模型) 【ML】基于机…...

工序排序问题--约翰逊法精讲
什么是约翰逊法?约翰逊法是作业排序中的一种排序方法。选出最短加工时间i*,若最短加工时间有多个,任选1个.若i*出现在机床1,它对应的工件先安排加工,否则放在最后安排,安排后划去该工件,重复上两个步骤,直…...

WebDAV之葫芦儿·派盘+网盘精灵
网盘精灵 支持WebDAV方式连接葫芦儿派盘。 推荐一款让您的iPhone、iPod、iPad 变成WebDav客户端的软件,支持从WebDav服务器连接葫芦儿派盘服务进行上传和下载件。 网盘精灵让您的iPhone、iPod、iPad 变成WebDav客户端。功能:WebDav操作、文件共享、本地文件管理...

计算机网络期末知识点总结
计算机网络期末知识点总结第四章—网络层:数据面4.1概述4.2虚电路和数据报网络4.3路由器工作原理4.4网际协议:因特网中的转发和编址第五章 网络层:控制面5.1路由选择算法5.2路由器中的路由选择5.3广播和多播路由选择第六章 链路层(…...

【Vue3 组件封装】vue3 轮播图组件封装
文章目录轮播图功能-获取数据轮播图-通用轮播图组件轮播图-数据渲染轮播图-逻辑封装轮播图功能-获取数据 目标: 基于pinia获取轮播图数据 核心代码: (1)在types/data.d.ts文件中定义轮播图数据的类型声明 // 所有接口的通用类型 export typ…...
电力国家(行业)标准目录
1、3~63kV交流高压负荷开关 GB 3804-90 代替 GB 3804-882、电气装置安装工程35kV及以下架空电力线路施工及验收规范Code for construction and acceptance of 35kVand umder over head power levels electricequipment installation engineeringGB50173—923、带电作…...

如何实现倒序输出
问题 如何实现字符串的大小写转换并倒序输出。 方法 采用Java自带的类方法进行倒序。 package homework4; public class Blog09 { public static void main(String[] args) { String a "HelloWord"; String a2 a.toUpperCase(); String a3 …...

遗留系统的自动化测试策略和实践方法
1 什么是遗留系统 遗留系统是一种旧的方法、旧的技术、旧的计算机系统或应用程序,属于或与以前的、过时的计算机系统有关,但仍在使用中。通常,将系统称为“遗留系统”意味着它可能已经过时或需要更换,但是系统还在对外提供服务,还在不断的迭代,有新的需求不断的交付。Ma…...

【Android】系统源码下载及编译
源码及编译 步骤 1:创建一个空目录来存放源码: mkdir aosp cd aosp步骤 2:获取最新版本的 repo 并签出 android-8.1.0_r1 分支: repo init -u https://android.googlesource.com/platform/manifest -b android-8.1.0_r1其中&am…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
