红黑树理论详解与Java实现
文章目录
- 基本定义
- 五大性质
- 红黑树和2-3-4树的关系
- 红黑树和2-3-4树各结点对应关系
- 添加结点到红黑树
- 注意事项
- 添加的所有情况
- 添加导致不平衡
- 叔父节点不是红色节点(祖父节点为红色)
- 添加不平衡LL/RR
- 添加不平衡LR/RL
- 叔父节点是红色节点(祖父节点为黑色)
- 删除
- 删除红色节点
- 删除黑色节点
- 删除黑色叶子节点——情况一
- 删除黑色叶子节点——情况二
- 删除黑色叶子节点——情况三
- 删除黑色叶子节点——情况四
- 红黑树与AVL(平衡二叉树)树比较
- 红黑树与B树B+树比较
- 完整的Java测试代码
- RedBlackTree
- BinaryTreeInfo
- BinaryTrees
- InorderPrinter
- LevelOrderPrinter
- Printer
- Strings
- 总结
基本定义
红黑树是一颗二叉搜索树,它在每个结点上增加了一个存储位来表示结点的颜色,可以是红色或者黑色。
通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是近似平衡的。
五大性质
1、结点必须是红色或者黑色。
2、根节点是黑色。
3、叶子结点(外部结点、空结点,不是传统上认为的那种叶子结点,如图中的那些NIL结点)都是黑色
4、红色结点的子结点都是黑色
于是有推论:
4.1、红色结点的父结点都是黑色
4.2、从根结点到叶子结点的所有路径上不能有两个连续的红色结点
5、从任一结点到叶子结点(外部结点、空结点,不是传统上认为的那种叶子结点,如图中的那些NIL结点)的所有路径都包含相同数目的黑色结点
如图所示:
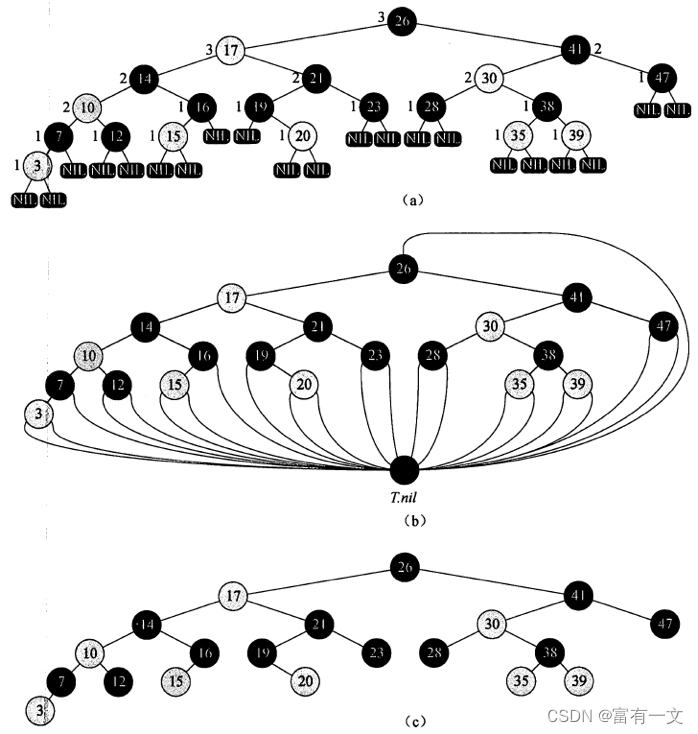
红黑树和2-3-4树的关系
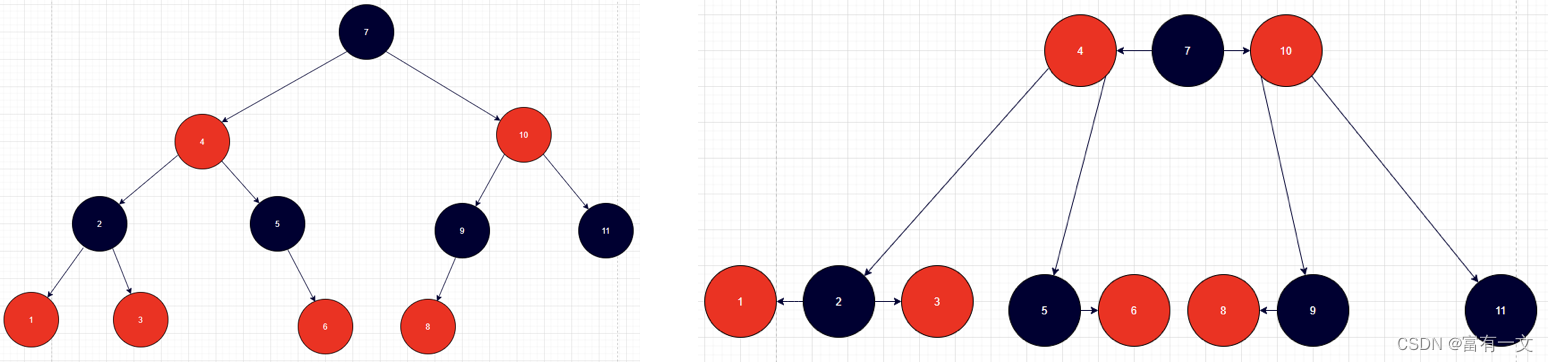
红黑树和4阶B树(2-3-4树)具有等价性
黑色节点与它的红色子节点融合在一起,形成一个B树节点
红黑树的黑色节点个数与4阶B树的节点总个数相等
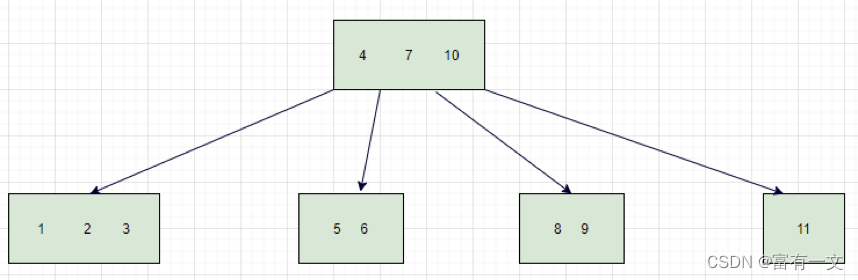
红黑树和2-3-4树各结点对应关系
红黑红、黑红、红黑、黑
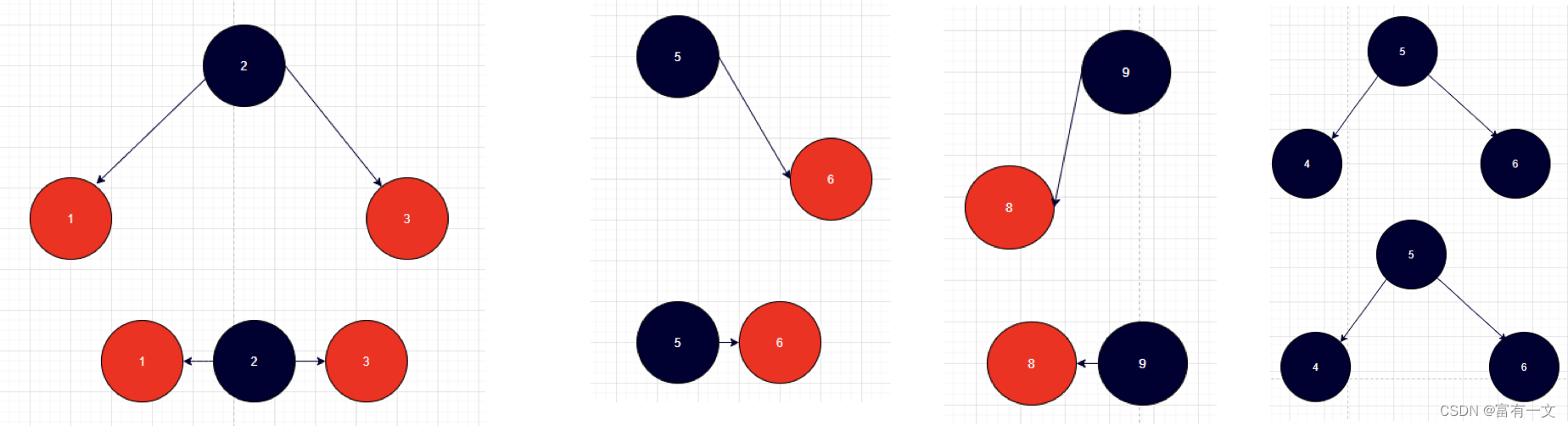
添加结点到红黑树
注意事项
一般新添加的节点默认为红色,这样对红黑树的性质影响最小(性质1、2、3、5都满足,性质4不一定)
如果新添加的节点是根节点,染成黑色即可
添加的所有情况
添加结点到红黑树总共有12中情况;
有4种情况满足红黑树的性质,父节点为黑色节点,因此不需要做任何处理。如下图所示的4种紫红色节点添加情况
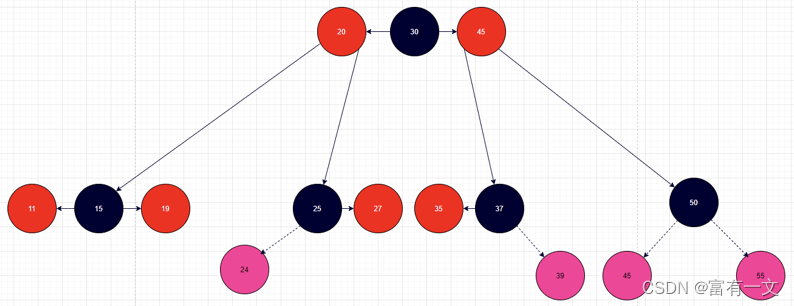
有8种情况不满足红黑树的性质,父节点为红色节点(但其实可以归纳为3种情况)。如下图所示的8种紫红色节点添加情况。
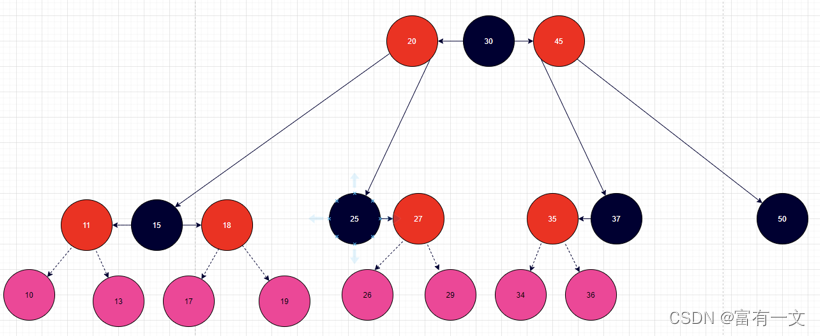
添加导致不平衡
添加结点导致红黑树出现不平衡的情况。
叔父节点不是红色节点(祖父节点为红色)
添加不平衡LL/RR
判断条件:叔父节点不是红色节点
父节点是祖父节点的左孩子,自己是父节点的左孩子(LL)
父节点是祖父节点的右孩子,自己是父节点的右孩子(RR)
如何恢复平衡:
1、父节点染成黑色,祖父节点染成红色
2、对祖父节点进行旋转操作(LL是右旋,RR是左旋)

添加不平衡LR/RL
判断条件:叔父节点不是红色节点
父节点是祖父节点的左孩子,自己是父节点的右孩子(LR)
父节点是祖父节点的右孩子,自己是父节点的左孩子(RL)
如何恢复平衡:
1、把自己染成黑色,祖父节点染成红色
2、进行两次旋转,第一次旋转是转换成LL/RR情况,第二次旋转恢复平衡
2.1、LR:先按照父节点左旋,变成LL,再按照祖父节点右旋
2.2、RL:先按照父节点右旋,变成RR,再按照祖父节点左旋

叔父节点是红色节点(祖父节点为黑色)
判断条件:叔父节点为红色
如何恢复平衡:
1、父节点、叔父节点都染成黑色
2、祖父节点染成红色,并把祖父节点当成新添加的节点,继续处理
2.1、如果祖父节点染成红色没有引起双红现象,则处理结束
2.2、如果祖父节点染成红色也导致双红现象,则继续按照是LL/RR,LR/RL,还是叔父节点为红色的三种情况处理,最差情况是处理直到根节点,把根节点染成了红色,这个时候只需要把根节点染成黑色即可。
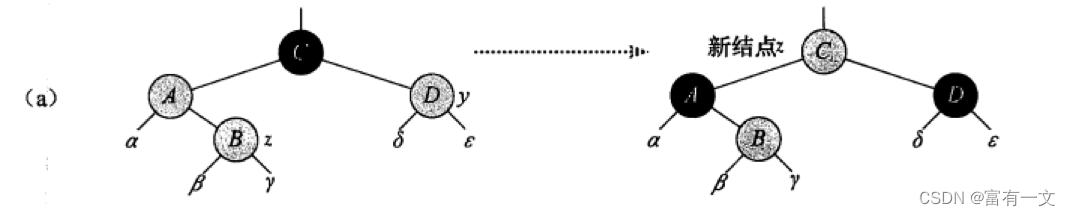
删除
B树中,最后真正被删除的元素都在叶子节点中。详细见B树(B-tree、B-树)理论详解
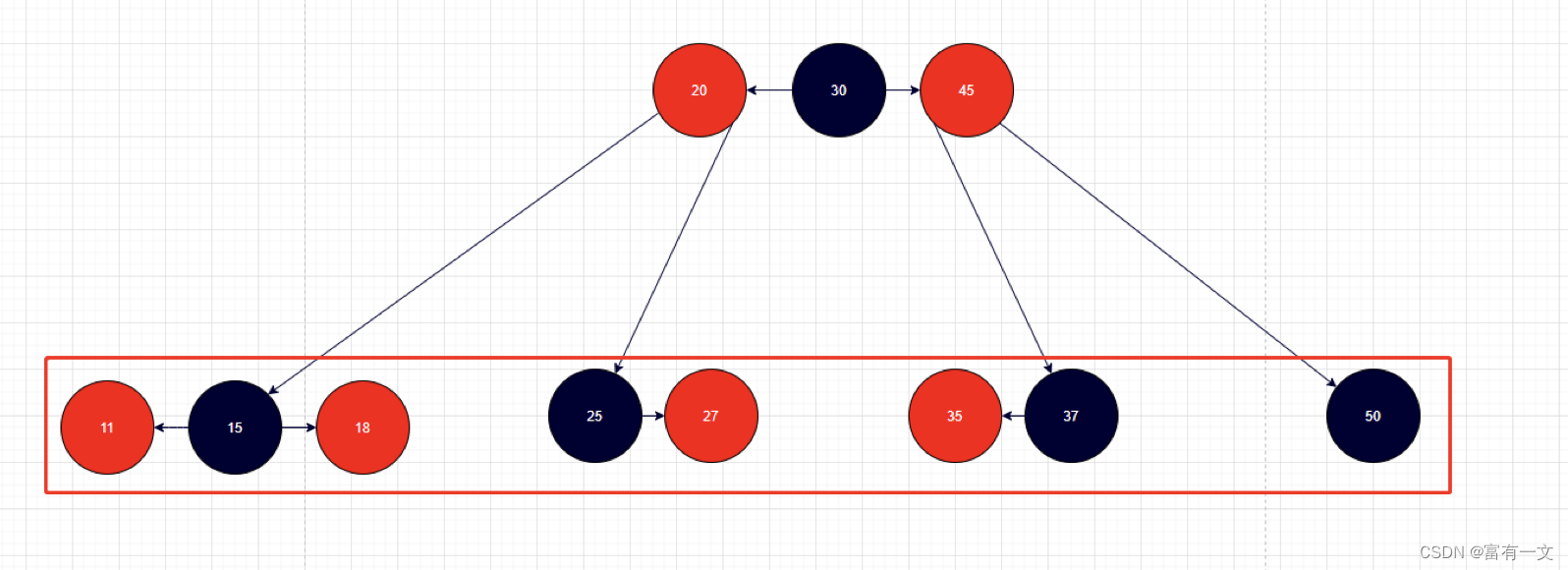
删除节点就是上面图的4种情况。
删除红色节点
直接删除,无需任何调整
删除黑色节点
有3种情况
1、拥有两个红色子节点的黑色节点不可能直接被删除,因为会找它的红色子节点替代删除,因此这种情况无需考虑
2、拥有1个红色子节点的黑色节点 (删除黑色节点后,把替代的红色子节点染成黑色即可)
3、黑色叶子节点 (情况比较复杂)
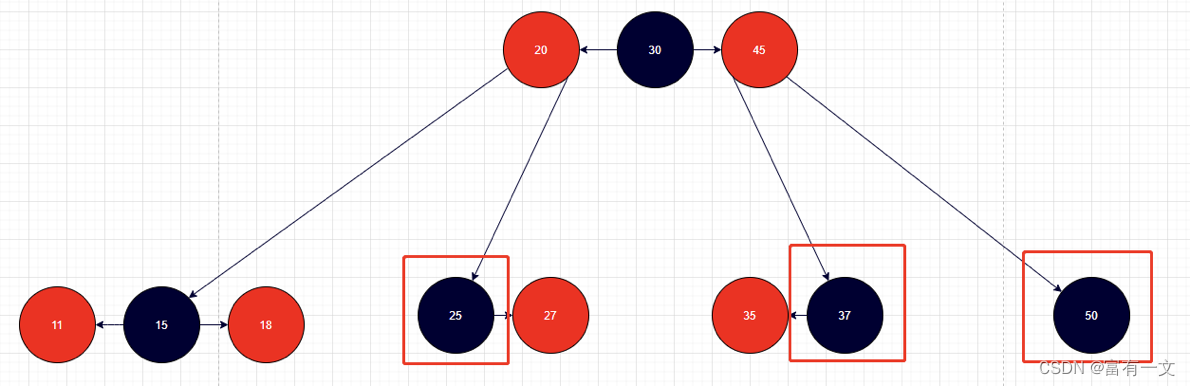
删除黑色叶子节点——情况一
如果兄弟节点是红色节点,
1、把兄弟节点染成黑色,父节点染成红色,对父节点进行旋转2、此时兄弟节点变成黑色,可以继续按照情况2,3,4进行处理
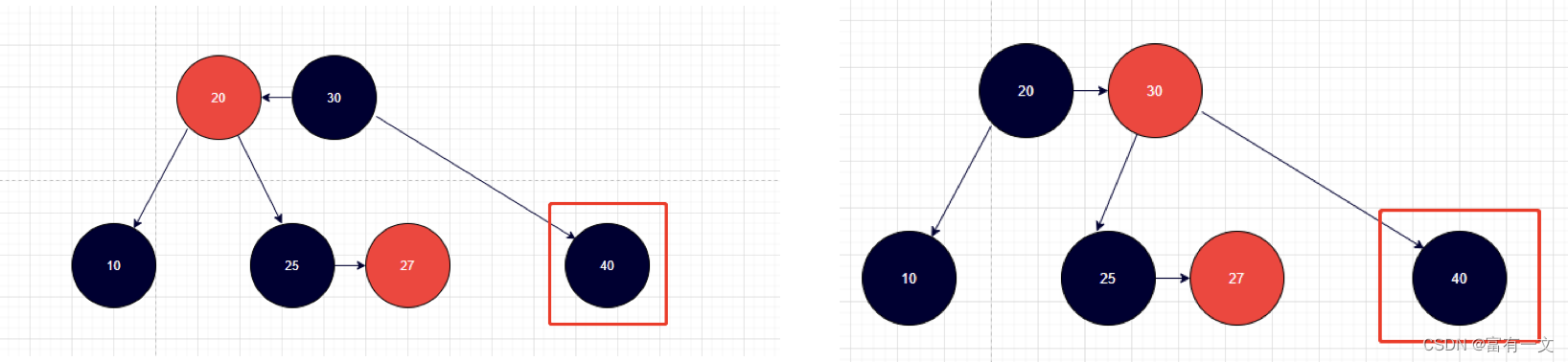
如图所示,40结点的兄弟结点是20,父结点是30。
删除黑色叶子节点——情况二
黑色兄弟节点没有一个红色子节点,
1、如果父节点是红色,把兄弟节点染成红色,父节点染成黑色,完成平衡维护。
2、如果父节点是黑色,把兄弟节点染成红色,把父节点当成待删除的节点,向上递归或循环处理(依然有情况1,2,3,4)。
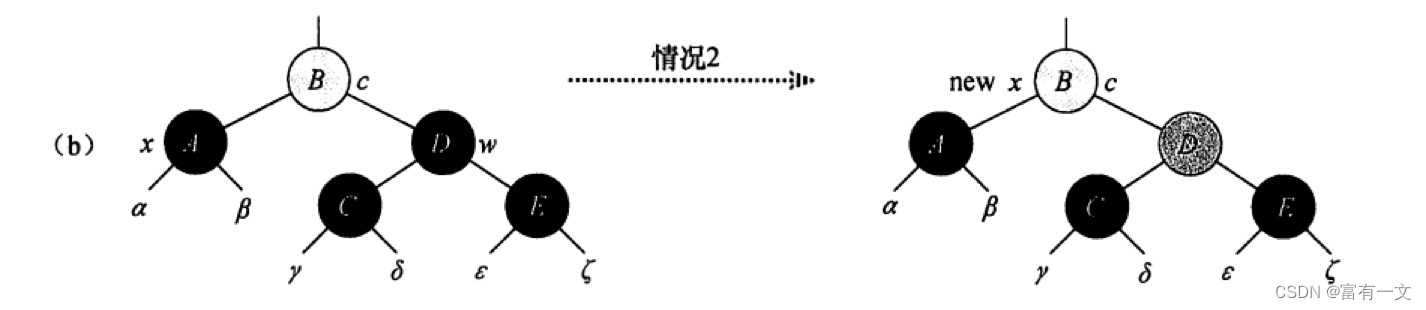
删除黑色叶子节点——情况三
兄弟节点是左节点,黑色兄弟节点的左孩子是黑色节点,为LR场景,需要先转变为LL,方便后面的平衡旋转。
1、把兄弟节点的右孩子设为黑色,兄弟节点设为红色,对兄弟节点进行左旋,确保兄弟节点有一个红色左孩子,此时变成情况4。

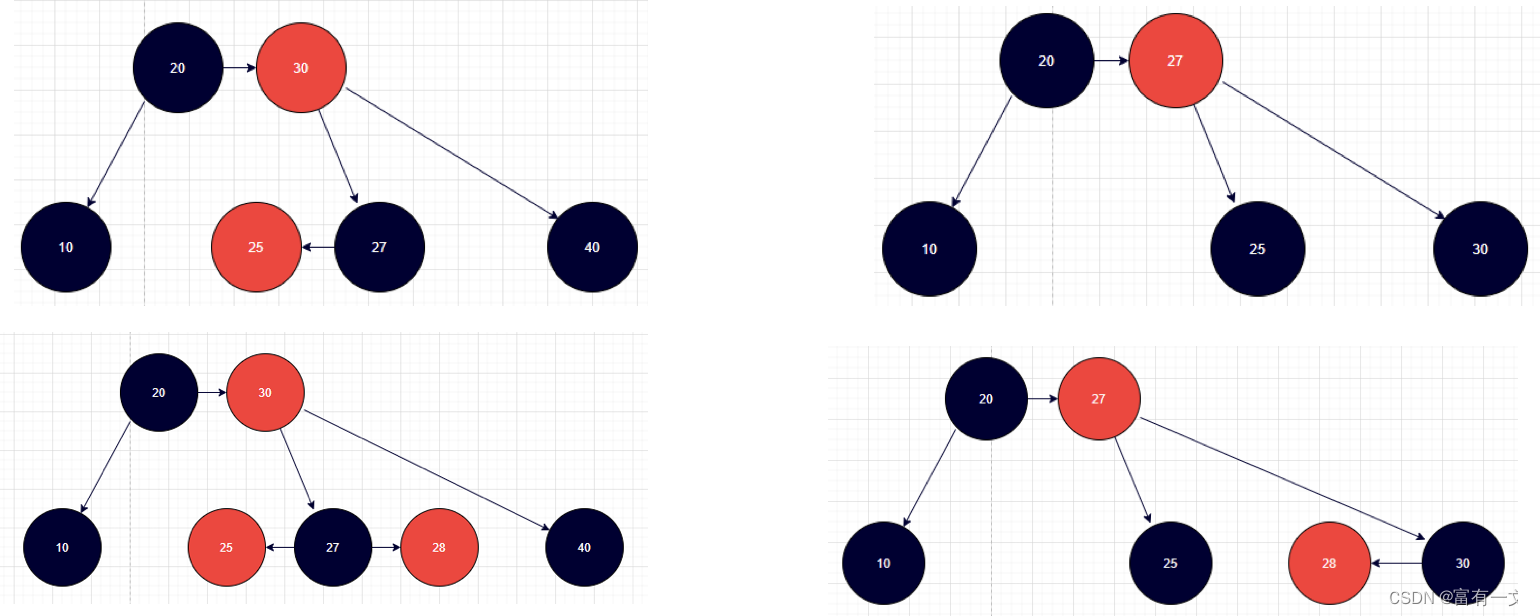
删除黑色叶子节点——情况四
兄弟节点是左节点,兄弟节点的左孩子是红色节点,LL场景,
1、把兄弟节点的颜色设置为父节点的颜色,父节点和兄弟节点的左孩子都设置为黑色,
对父节点进行右旋,恢复平衡。
红黑树与AVL(平衡二叉树)树比较
AVL树的平衡标准比较严格:每个左右子树的高度差不超过1。
红黑树的平衡标准比较宽松:没有一条路径会大于其他路径的两倍。
相对于AVL树来说,红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,总体性能要优于 AVL树。
红黑树的平均统计性能优于AVL树,实际应用中更多选择使用红黑树。
红黑树与B树B+树比较
红黑树的分叉少,适合在内存中使用,如果在硬盘中使用的话,当数据量大的时候,红黑树的层高比较高,会带来比较多的磁盘IO,影响查询性能,比如说100万的数据量,用红黑树的话,大概是20层的层高,会有20次磁盘IO。
B树和B+树的分叉比较多,B树分叉一般能到两三百,B+树分叉多的能到上千,所以B树和B+树适合磁盘存储,100万的数据量,一般3层树高即可搞定,只有3次磁盘IO,实际中数据库一般把根节点存放在内存中,所以其实只有两次IO。
完整的Java测试代码
RedBlackTree
package redblacktree;public class RedBlackTree implements BinaryTreeInfo {//红黑直接用布尔变量定义private static final boolean RED = false;private static final boolean BLACK = true;//初始化一个唯一的叶结点private final RBNode nil = new RBNode();//根结点初始化为nilprivate RBNode root = nil;public RBNode getRoot() {return root;}public void setRoot(RBNode root) {this.root = root;}public RedBlackTree() {this.root = nil;}public RedBlackTree(RBNode root) {this.root = root;}//前序遍历二叉树public void preorderTreeWalk(RBNode x) {if(x != nil) {System.out.print(x.key + " ");preorderTreeWalk(x.left);preorderTreeWalk(x.right);}}//中序遍历二叉树public void inorderTreeWalk(RBNode x) {if(x != nil) {inorderTreeWalk(x.left);System.out.print(x.key + " ");inorderTreeWalk(x.right);}}//后序遍历二叉树public void postorderTreeWalk(RBNode x) {if(x != nil) {postorderTreeWalk(x.left);postorderTreeWalk(x.right);System.out.print(x.key + " ");}}//在二叉搜索树中查询某个值,递归版本public RBNode treeSearch(RBNode x, Integer k) {if(x == nil || k == x.key) {return x;}if(k < x.key) {return treeSearch(x.left, k);} else {return treeSearch(x.right, k);}}//在二叉搜索树中查询某个值,循环版本public RBNode iterativeTreeSearch(RBNode x, Integer k) {while(x != nil && k != x.key) {if(k < x.key) {x = x.left;} else {x = x.right;}}return x;}//在二叉搜索树中查找包含最小值的节点public RBNode treeMinimum(RBNode x) {while (x.left != nil) {x = x.left;}return x;}//在二叉搜索树中查找包含最大值的节点public RBNode treeMaximum(RBNode x) {while (x.right != nil) {x = x.right;}return x;}//查找节点x的后继节点public RBNode treeSuccessor(RBNode x) {if(x.right != nil) { //x的右子树不为空,找右子树的最小值return treeMinimum(x.right);}RBNode y = x.parent;while(y != nil && x == y.right) {x = y;y = y.parent;}return y;}//查找节点x的前驱节点public RBNode treePredeceessor(RBNode x) {if(x.left != nil) {return treeMaximum(x.left);}RBNode y = x.parent;while(y != nil && x == y.left) {x = y;y = y.parent;}return y;}/*** 围绕x左旋* xp xp* / /* x xr* / \ ==> / \* xl xr x rr* / \ / \* rl rr xl rl** @param t,x*/void leftRotate(RedBlackTree t, RBNode x) {RBNode y = x.right; //让y等于x的右子节点x.right = y.left; //将y的左子树转成x的右子树if(y.left != t.nil) { //假如y的左孩子不为空,将y的左孩子的父亲设置为xy.left.parent = x;}y.parent = x.parent; //将y的父亲设置为x的父亲if(x.parent == t.nil) {t.root = y; //考虑x原来为根节点的情况} else if (x.parent.left == x) {x.parent.left = y;} else {x.parent.right = y;}y.left = x;x.parent = y;}/*** 围绕x右旋* xp xp* \ \* x xl* / \ => / \* xl xr ll x* / \ / \* ll lr lr xr** @param t,x*/void rightRotate(RedBlackTree t, RBNode x) {RBNode y = x.left; //让y等于x的左子节点x.left = y.right; //将y的右子树转成x的左子树if(y.right != t.nil) { //假如y的右孩子不为空,将y的右孩子的父亲设置为xy.right.parent = x;}y.parent = x.parent; //将y的父亲设置为x的父亲if(x.parent == t.nil) {t.root = y; //考虑x原来为根节点的情况} else if (x.parent.left == x) {x.parent.left = y;} else {x.parent.right = y;}y.right = x;x.parent = y;}//红黑树的插入操作public void RBInsert(RedBlackTree t, RBNode z) {RBNode y = t.nil;RBNode x = t.root;while(x != t.nil) {y = x;if(z.key < x.key) {x = x.left;} else {x = x.right;}}z.parent = y;if(y == t.nil) { //说明现在是棵空树t.root = z;} else if (z.key < y.key) {y.left = z;} else {y.right = z;}z.left = t.nil;z.right = t.nil;z.color = RED;rbInsertFixup(t, z);}//插入节点后维护红黑树性质的过程public void rbInsertFixup(RedBlackTree t, RBNode z) {while (z.parent.color == RED) {if(z.parent == z.parent.parent.left) { //z的父节点是z的祖父节点的左孩子RBNode y = z.parent.parent.right; //让y成为z的叔叔节点if (y.color == RED) {/** z的父亲和叔叔节点都是红色,* 根据红黑树性质,z的祖父一定是黑色* 所以这时候,可以把z的祖父设为红色,* z的父亲和叔叔都设为黑色,但这可能* 导致z的祖父产生双红节点的问题,这* 时候把z设置成z的祖父,继续向上递归*/z.parent.color = BLACK;y.color = BLACK;z.parent.parent.color = RED;z = z.parent.parent;} else {if (z == z.parent.right) {/** z的父亲是左节点,z是右节点,* 满足LR不平衡,需要对z的父亲进行左旋,* 转变成LL不平衡*/z = z.parent;leftRotate(t, z);}/** z的父亲是左节点,z也是左节点,* 满足LL不平衡,把z的父亲设为黑色,* z的祖父设为红色,对z进行右旋,* 即可满足平衡*/z.parent.color = BLACK;z.parent.parent.color = RED;rightRotate(t, z.parent.parent);}} else {RBNode y = z.parent.parent.left; //让y成为z的叔叔节点if (y.color == RED) {/** z的父亲和叔叔节点都是红色,* 根据红黑树性质,z的祖父一定是黑色* 所以这时候,可以把z的祖父设为红色,* z的父亲和叔叔都设为黑色,但这可能* 导致z的祖父产生双红节点的问题,这* 时候把z设置成z的祖父,继续向上递归*/z.parent.color = BLACK;y.color = BLACK;z.parent.parent.color = RED;z = z.parent.parent;} else {if (z == z.parent.left) {/** z的父亲是右节点,z是左节点,* 满足RL不平衡,需要对z的父亲进行右旋,* 转变成RR不平衡*/z = z.parent;rightRotate(t, z);}/** z的父亲是右节点,z也是右节点,* 满足RR不平衡,把z的父亲设为黑色,* z的祖父设为红色,对z进行左旋,* 即可满足平衡*/z.parent.color = BLACK;z.parent.parent.color = RED;leftRotate(t, z.parent.parent);}}}t.root.color = BLACK;}public void rbTransplant(RedBlackTree t, RBNode u, RBNode v) {if(u.parent == t.nil) {t.root = v;} else if(u == u.parent.left) {u.parent.left = v;} else {u.parent.right = v;}v.parent = u.parent;}//删除节点操作public void rbDelete(RedBlackTree t, RBNode z) {RBNode x;RBNode y = z;boolean yOriginalColor = y.color;if (z.left == t.nil) {x = z.right;//z的左孩子为空,用z的右孩子替换z,此时z的右孩子可以为空,也可以不为空rbTransplant(t, z, z.right);} else if (z.right == t.nil) {x = z.left;//z仅有一个孩子且其为左孩子,用z的左孩子替换zrbTransplant(t, z , z.left);} else {//z有两个孩子,找z的后继节点y = treeMinimum(z.right);yOriginalColor = y.color;x = y.right;if(y.parent == z) {x.parent = y;} else {//用以y的右孩子为根的树代替以y为根的树rbTransplant(t, y, y.right);y.right = z.right;y.right.parent = y;}//用以y为根的树代替以z为根的树rbTransplant(t, z, y);y.left = z.left;y.left.parent = y;}//如果删除的为黑节点,需要修复平衡if (yOriginalColor == BLACK) {
// rbDeleteFixup(t, x);fixAfterDelete(t, x);}}//删除修复算法导论版代码,用红黑树解释public void rbDeleteFixup(RedBlackTree t, RBNode x) {while(x != t.root && x.color == BLACK) {//x是左孩子if(x == x.parent.left) {//w为兄弟节点RBNode w = x.parent.right;//w为红色,要旋转成黑色,方便后续操作if(w.color == RED) {w.color = BLACK;x.parent.color = RED;leftRotate(t, x.parent);//此时w为黑色w = x.parent.right;}/** w是黑色,w的两个孩子都是黑色,* 没办法通过旋转恢复平衡,只能把w拉下水,设为红色,* x变成x的父节点,向上递归*/if(w.left.color == BLACK && w.right.color == BLACK) {w.color = RED;x = x.parent;} else {/** w是黑色,w的右孩子是黑色,* w的左孩子是红色,为RL场景* 此时把w的左孩子设为黑色,* w设为红色,对w进行右旋,* 确保w的右孩子为红色,此时为RR场景*/if(w.right.color == BLACK) {w.left.color = BLACK;w.color = RED;rightRotate(t, w);w = x.parent.right;}/** 此时一定是w为黑色,w的右孩子为红色,* w设置为x父节点的颜色,* x父节点设为黑色,* w的右孩子设置为黑色,* 这样w路径上多出来一个黑节点,* 对x的父节点进行左旋,* 相当于把原来w路径上多出来的黑节点补充到x的路径上,* 这样就填补了原来删除的黑节点,恢复平衡*/w.color = x.parent.color;x.parent.color = BLACK;w.right.color = BLACK;leftRotate(t, x.parent);/** 这里已经恢复平衡,* 所以直接把x设置为根节点结束循环*/x = t.root;}} else {//x是右孩子,w是兄弟节点RBNode w = x.parent.left;//w为红色,要旋转成黑色,方便后续操作if(w.color == RED) {w.color = BLACK;x.parent.color = RED;rightRotate(t, x.parent);//此时w为黑色w = x.parent.right;}/** w是黑色,w的两个孩子都是黑色,* 没办法通过旋转恢复平衡,只能把w拉下水,设为红色,* x变成x的父节点,向上递归*/if(w.right.color == BLACK && w.left.color == BLACK) {w.color = RED;x = x.parent;} else {/** w是黑色,w的左孩子是黑色,* w的右孩子是红色,为LR场景* 此时把w的右孩子设为黑色,* w设为红色,对w进行左旋,* 确保w的左孩子一定为红色,此时为LL场景*/if(w.left.color == BLACK) {w.right.color = BLACK;w.color = RED;leftRotate(t, w);w = x.parent.left;}/** 此时一定是w为黑色,w的左孩子为红色,* w设置为x父节点的颜色,* x父节点设为黑色,* w的左孩子设置为黑色,* 这样w路径上多出来一个黑节点,* 对x的父节点进行右旋,* 相当于把原来w路径上多出来的黑节点补充到x的路径上,* 这样就填补了原来删除的黑节点,恢复平衡*/w.color = x.parent.color;x.parent.color = BLACK;w.left.color = BLACK;rightRotate(t, x.parent);/** 这里已经恢复平衡,* 所以直接把x设置为根节点结束循环*/x = t.root;}}}/** 循环结束,要么x是根节点,* 要么x是红色节点,* 直接把x设置成黑色,即可恢复平衡*/x.color = BLACK;}/*** 根据2-3-4树解释的红黑树删除* 删除后的调整处理* 1.情况1:自己能搞定,对应的叶子节点是3节点或者4节点* 2.情况2:自己搞不定,需要兄弟节点借,但是兄弟节点不能直接借,找父亲节点借,父亲下来,然后兄弟节点找一个人代替父亲当家* 3.情况3:跟兄弟节点借,兄弟也没有* @param t,x*/public void fixAfterDelete(RedBlackTree t, RBNode x){while(x != t.root && x.color == BLACK){//x是左孩子的情况if(x == x.parent.left) {//兄弟节点RBNode w = x.parent.right;//判断此时兄弟节点是否是真正的兄弟节点,只有黑色节点才是if(w.color == RED){w.color = BLACK;x.parent.color = RED;leftRotate(t, x.parent);//找到真正的兄弟节点w = x.parent.right;}//情况三,找兄弟借,兄弟没得借if(w.left.color == BLACK && w.right.color == BLACK) {//把兄弟拉下水,设为红色,向上递归w.color = RED;x = x.parent;}//情况二,找兄弟借,兄弟有的借else{//确保w的右孩子是红色if(w.right.color == BLACK) {w.left.color = BLACK;w.color = RED;rightRotate(t, w);w = x.parent.right;}/** 此时一定是w为黑色,w的右孩子为红色,* w设置为x父节点的颜色,* x父节点设为黑色,* w的右孩子设置为黑色,* 这样w路径上多出来一个黑节点,* 对x的父节点进行左旋,* 相当于把原来w路径上多出来的黑节点补充到x的路径上,* 这样就填补了原来删除的黑节点,恢复平衡*/w.color = x.parent.color;x.parent.color = BLACK;w.right.color = BLACK;leftRotate(t, x.parent);x = t.root;}}//x是右孩子的情况else{//兄弟节点RBNode w = x.parent.left;//判断此时兄弟节点是否是真正的兄弟节点,只有黑色节点才是if(w.color == RED) {w.color = BLACK;x.parent.color = RED;rightRotate(t, x.parent);//此时w为黑色,才是真正的兄弟节点w = x.parent.right;}//情况三,找兄弟借,兄弟没得借if(w.left.color == BLACK && w.right.color == BLACK) {//把兄弟拉下水,设为红色,向上递归w.color = RED;x = x.parent;}//情况二,找兄弟借,兄弟有的借else{//确保w的左孩子是红色if(w.left.color == BLACK) {w.right.color = BLACK;w.color = RED;leftRotate(t, w);w = x.parent.right;}/** 此时一定是w为黑色,w的左孩子为红色,* w设置为x父节点的颜色,* x父节点设为黑色,* w的左孩子设置为黑色,* 这样w路径上多出来一个黑节点,* 对x的父节点进行右旋,* 相当于把原来w路径上多出来的黑节点补充到x的路径上,* 这样就填补了原来删除的黑节点,恢复平衡*/w.color = x.parent.color;x.parent.color = BLACK;w.left.color = BLACK;rightRotate(t, x.parent);x = t.root;}}}//情况一、替代节点是红色,则直接染红,补偿删除的黑色节点,这样红黑树依然保持平衡x.color = BLACK;}//红黑树节点类定义static class RBNode {private Integer key; //节点值private RBNode parent; //父节点private RBNode left; //左孩子private RBNode right; //右孩子private boolean color = BLACK;public RBNode() {}public RBNode(Integer key) {this.key = key;}public RBNode(Integer key, RBNode parent) {this.parent = parent;this.color = BLACK;this.key = key;}public RBNode(RBNode parent, RBNode left, RBNode right, Integer key, boolean color) {this.parent = parent;this.left = left;this.right = right;this.key = key;this.color = color;}public Integer getKey() {return key;}public void setKey(Integer key) {this.key = key;}public RBNode getParent() {return parent;}public void setParent(RBNode parent) {this.parent = parent;}public RBNode getLeft() {return left;}public void setLeft(RBNode left) {this.left = left;}public RBNode getRight() {return right;}public void setRight(RBNode right) {this.right = right;}}@Overridepublic Object root() {return root;}@Overridepublic Object left(Object RBNode) {return ((RBNode)RBNode).left;}@Overridepublic Object right(Object RBNode) {return ((RBNode)RBNode).right;}@Overridepublic Object string(Object RBNode) {RBNode myRBNode = (RBNode)RBNode;String color = myRBNode.color == RED ? "RED" : "BLACK";return myRBNode.key + "(" + color + ")";}public static void main(String[] args) {RedBlackTree bst = new RedBlackTree();bst.RBInsert(bst, new RBNode(12));bst.RBInsert(bst, new RBNode(5));bst.RBInsert(bst, new RBNode(2));bst.RBInsert(bst, new RBNode(9));bst.RBInsert(bst, new RBNode(18));bst.RBInsert(bst, new RBNode(15));bst.RBInsert(bst, new RBNode(19));bst.RBInsert(bst, new RBNode(17));bst.inorderTreeWalk(bst.root);System.out.println();BinaryTrees.print(bst);bst.rbDelete(bst, bst.treeSearch(bst.root, 12));System.out.println();BinaryTrees.print(bst);}
}BinaryTreeInfo
package redblacktree;public interface BinaryTreeInfo {/*** who is the root node*/Object root();/*** how to get the left child of the node*/Object left(Object node);/*** how to get the right child of the node*/Object right(Object node);/*** how to print the node*/Object string(Object node);
}BinaryTrees
package redblacktree;public final class BinaryTrees {private BinaryTrees() {}public static void print(BinaryTreeInfo tree) {print(tree, null);}public static void println(BinaryTreeInfo tree) {println(tree, null);}public static void print(BinaryTreeInfo tree, PrintStyle style) {if (tree == null || tree.root() == null) return;printer(tree, style).print();}public static void println(BinaryTreeInfo tree, PrintStyle style) {if (tree == null || tree.root() == null) return;printer(tree, style).println();}public static String printString(BinaryTreeInfo tree) {return printString(tree, null);}public static String printString(BinaryTreeInfo tree, PrintStyle style) {if (tree == null || tree.root() == null) return null;return printer(tree, style).printString();}private static Printer printer(BinaryTreeInfo tree, PrintStyle style) {if (style == PrintStyle.INORDER) return new InorderPrinter(tree);return new LevelOrderPrinter(tree);}public enum PrintStyle {LEVEL_ORDER, INORDER}
}
InorderPrinter
package redblacktree;/**┌──800┌──760│ └──600┌──540│ └──476│ └──445┌──410│ └──394
381│ ┌──190│ │ └──146│ ┌──40│ │ └──35└──12└──9*/
public class InorderPrinter extends Printer {private static String rightAppend;private static String leftAppend;private static String blankAppend;private static String lineAppend;static {int length = 2;rightAppend = "┌" + Strings.repeat("─", length);leftAppend = "└" + Strings.repeat("─", length);blankAppend = Strings.blank(length + 1);lineAppend = "│" + Strings.blank(length);}public InorderPrinter(BinaryTreeInfo tree) {super(tree);}@Overridepublic String printString() {StringBuilder string = new StringBuilder(printString(tree.root(), "", "", ""));string.deleteCharAt(string.length() - 1);return string.toString();}/*** 生成node节点的字符串* @param nodePrefix node那一行的前缀字符串* @param leftPrefix node整棵左子树的前缀字符串* @param rightPrefix node整棵右子树的前缀字符串* @return*/private String printString(Object node,String nodePrefix,String leftPrefix,String rightPrefix) {Object left = tree.left(node);Object right = tree.right(node);String string = tree.string(node).toString();int length = string.length();if (length % 2 == 0) {length--;}length >>= 1;String nodeString = "";if (right != null) {rightPrefix += Strings.blank(length);nodeString += printString(right, rightPrefix + rightAppend, rightPrefix + lineAppend, rightPrefix + blankAppend);}nodeString += nodePrefix + string + "\n";if (left != null) {leftPrefix += Strings.blank(length);nodeString += printString(left, leftPrefix + leftAppend, leftPrefix + blankAppend, leftPrefix + lineAppend);}return nodeString;}
}LevelOrderPrinter
package redblacktree;import java.util.*;/**┌───381────┐│ │
┌─12─┐ ┌─410─┐
│ │ │ │
9 ┌─40─┐ 394 ┌─540─┐│ │ │ │35 ┌─190 ┌─476 ┌─760─┐│ │ │ │146 445 600 800*/
public class LevelOrderPrinter extends Printer {/*** 节点之间允许的最小间距(最小只能填1)*/private static final int MIN_SPACE = 1;private Node root;private int minX;private int maxWidth;private List<List<Node>> nodes;public LevelOrderPrinter(BinaryTreeInfo tree) {super(tree);root = new Node(tree.root(), tree);maxWidth = root.width;}@Overridepublic String printString() {// nodes用来存放所有的节点nodes = new ArrayList<>();fillNodes();cleanNodes();compressNodes();addLineNodes();int rowCount = nodes.size();// 构建字符串StringBuilder string = new StringBuilder();for (int i = 0; i < rowCount; i++) {if (i != 0) {string.append("\n");}List<Node> rowNodes = nodes.get(i);StringBuilder rowSb = new StringBuilder();for (Node node : rowNodes) {int leftSpace = node.x - rowSb.length() - minX;rowSb.append(Strings.blank(leftSpace));rowSb.append(node.string);}string.append(rowSb);}return string.toString();}/*** 添加一个元素节点*/private Node addNode(List<Node> nodes, Object btNode) {Node node = null;if (btNode != null) {node = new Node(btNode, tree);maxWidth = Math.max(maxWidth, node.width);nodes.add(node);} else {nodes.add(null);}return node;}/*** 以满二叉树的形式填充节点*/private void fillNodes() {// 第一行List<Node> firstRowNodes = new ArrayList<>();firstRowNodes.add(root);nodes.add(firstRowNodes);// 其他行while (true) {List<Node> preRowNodes = nodes.get(nodes.size() - 1);List<Node> rowNodes = new ArrayList<>();boolean notNull = false;for (Node node : preRowNodes) {if (node == null) {rowNodes.add(null);rowNodes.add(null);} else {Node left = addNode(rowNodes, tree.left(node.btNode));if (left != null) {node.left = left;left.parent = node;notNull = true;}Node right = addNode(rowNodes, tree.right(node.btNode));if (right != null) {node.right = right;right.parent = node;notNull = true;}}}// 全是null,就退出if (!notNull) break;nodes.add(rowNodes);}}/*** 删除全部null、更新节点的坐标*/private void cleanNodes() {int rowCount = nodes.size();if (rowCount < 2) return;// 最后一行的节点数量int lastRowNodeCount = nodes.get(rowCount - 1).size();// 每个节点之间的间距int nodeSpace = maxWidth + 2;// 最后一行的长度int lastRowLength = lastRowNodeCount * maxWidth + nodeSpace * (lastRowNodeCount - 1);// 空集合Collection<Object> nullSet = Collections.singleton(null);for (int i = 0; i < rowCount; i++) {List<Node> rowNodes = nodes.get(i);int rowNodeCount = rowNodes.size();// 节点左右两边的间距int allSpace = lastRowLength - (rowNodeCount - 1) * nodeSpace;int cornerSpace = allSpace / rowNodeCount - maxWidth;cornerSpace >>= 1;int rowLength = 0;for (int j = 0; j < rowNodeCount; j++) {if (j != 0) {// 每个节点之间的间距rowLength += nodeSpace;}rowLength += cornerSpace;Node node = rowNodes.get(j);if (node != null) {// 居中(由于奇偶数的问题,可能有1个符号的误差)int deltaX = (maxWidth - node.width) >> 1;node.x = rowLength + deltaX;node.y = i;}rowLength += maxWidth;rowLength += cornerSpace;}// 删除所有的nullrowNodes.removeAll(nullSet);}}/*** 压缩空格*/private void compressNodes() {int rowCount = nodes.size();if (rowCount < 2) return;for (int i = rowCount - 2; i >= 0; i--) {List<Node> rowNodes = nodes.get(i);for (Node node : rowNodes) {Node left = node.left;Node right = node.right;if (left == null && right == null) continue;if (left != null && right != null) {// 让左右节点对称node.balance(left, right);// left和right之间可以挪动的最小间距int leftEmpty = node.leftBoundEmptyLength();int rightEmpty = node.rightBoundEmptyLength();int empty = Math.min(leftEmpty, rightEmpty);empty = Math.min(empty, (right.x - left.rightX()) >> 1);// left、right的子节点之间可以挪动的最小间距int space = left.minLevelSpaceToRight(right) - MIN_SPACE;space = Math.min(space >> 1, empty);// left、right往中间挪动if (space > 0) {left.translateX(space);right.translateX(-space);}// 继续挪动space = left.minLevelSpaceToRight(right) - MIN_SPACE;if (space < 1) continue;// 可以继续挪动的间距leftEmpty = node.leftBoundEmptyLength();rightEmpty = node.rightBoundEmptyLength();if (leftEmpty < 1 && rightEmpty < 1) continue;if (leftEmpty > rightEmpty) {left.translateX(Math.min(leftEmpty, space));} else {right.translateX(-Math.min(rightEmpty, space));}} else if (left != null) {left.translateX(node.leftBoundEmptyLength());} else { // right != nullright.translateX(-node.rightBoundEmptyLength());}}}}private void addXLineNode(List<Node> curRow, Node parent, int x) {Node line = new Node("─");line.x = x;line.y = parent.y;curRow.add(line);}private Node addLineNode(List<Node> curRow, List<Node> nextRow, Node parent, Node child) {if (child == null) return null;Node top = null;int topX = child.topLineX();if (child == parent.left) {top = new Node("┌");curRow.add(top);for (int x = topX + 1; x < parent.x; x++) {addXLineNode(curRow, parent, x);}} else {for (int x = parent.rightX(); x < topX; x++) {addXLineNode(curRow, parent, x);}top = new Node("┐");curRow.add(top);}// 坐标top.x = topX;top.y = parent.y;child.y = parent.y + 2;minX = Math.min(minX, child.x);// 竖线Node bottom = new Node("│");bottom.x = topX;bottom.y = parent.y + 1;nextRow.add(bottom);return top;}private void addLineNodes() {List<List<Node>> newNodes = new ArrayList<>();int rowCount = nodes.size();if (rowCount < 2) return;minX = root.x;for (int i = 0; i < rowCount; i++) {List<Node> rowNodes = nodes.get(i);if (i == rowCount - 1) {newNodes.add(rowNodes);continue;}List<Node> newRowNodes = new ArrayList<>();newNodes.add(newRowNodes);List<Node> lineNodes = new ArrayList<>();newNodes.add(lineNodes);for (Node node : rowNodes) {addLineNode(newRowNodes, lineNodes, node, node.left);newRowNodes.add(node);addLineNode(newRowNodes, lineNodes, node, node.right);}}nodes.clear();nodes.addAll(newNodes);}private static class Node {/*** 顶部符号距离父节点的最小距离(最小能填0)*/private static final int TOP_LINE_SPACE = 1;Object btNode;Node left;Node right;Node parent;/*** 首字符的位置*/int x;int y;int treeHeight;String string;int width;private void init(String string) {string = (string == null) ? "null" : string;string = string.isEmpty() ? " " : string;width = string.length();this.string = string;}public Node(String string) {init(string);}public Node(Object btNode, BinaryTreeInfo opetaion) {init(opetaion.string(btNode).toString());this.btNode = btNode;}/*** 顶部方向字符的X(极其重要)* * @return*/private int topLineX() {// 宽度的一半int delta = width;if (delta % 2 == 0) {delta--;}delta >>= 1;if (parent != null && this == parent.left) {return rightX() - 1 - delta;} else {return x + delta;}}/*** 右边界的位置(rightX 或者 右子节点topLineX的下一个位置)(极其重要)*/private int rightBound() {if (right == null) return rightX();return right.topLineX() + 1;}/*** 左边界的位置(x 或者 左子节点topLineX)(极其重要)*/private int leftBound() {if (left == null) return x;return left.topLineX();}/*** x ~ 左边界之间的长度(包括左边界字符)* * @return*/private int leftBoundLength() {return x - leftBound();}/*** rightX ~ 右边界之间的长度(包括右边界字符)* * @return*/private int rightBoundLength() {return rightBound() - rightX();}/*** 左边界可以清空的长度* * @return*/private int leftBoundEmptyLength() {return leftBoundLength() - 1 - TOP_LINE_SPACE;}/*** 右边界可以清空的长度* * @return*/private int rightBoundEmptyLength() {return rightBoundLength() - 1 - TOP_LINE_SPACE;}/*** 让left和right基于this对称*/private void balance(Node left, Node right) {if (left == null || right == null) return;// 【left的尾字符】与【this的首字符】之间的间距int deltaLeft = x - left.rightX();// 【this的尾字符】与【this的首字符】之间的间距int deltaRight = right.x - rightX();int delta = Math.max(deltaLeft, deltaRight);int newRightX = rightX() + delta;right.translateX(newRightX - right.x);int newLeftX = x - delta - left.width;left.translateX(newLeftX - left.x);}private int treeHeight(Node node) {if (node == null) return 0;if (node.treeHeight != 0) return node.treeHeight;node.treeHeight = 1 + Math.max(treeHeight(node.left), treeHeight(node.right));return node.treeHeight;}/*** 和右节点之间的最小层级距离*/private int minLevelSpaceToRight(Node right) {int thisHeight = treeHeight(this);int rightHeight = treeHeight(right);int minSpace = Integer.MAX_VALUE;for (int i = 0; i < thisHeight && i < rightHeight; i++) {int space = right.levelInfo(i).leftX - this.levelInfo(i).rightX;minSpace = Math.min(minSpace, space);}return minSpace;}private LevelInfo levelInfo(int level) {if (level < 0) return null;int levelY = y + level;if (level >= treeHeight(this)) return null;List<Node> list = new ArrayList<>();Queue<Node> queue = new LinkedList<>();queue.offer(this);// 层序遍历找出第level行的所有节点while (!queue.isEmpty()) {Node node = queue.poll();if (levelY == node.y) {list.add(node);} else if (node.y > levelY) break;if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}Node left = list.get(0);Node right = list.get(list.size() - 1);return new LevelInfo(left, right);}/*** 尾字符的下一个位置*/public int rightX() {return x + width;}public void translateX(int deltaX) {if (deltaX == 0) return;x += deltaX;// 如果是LineNodeif (btNode == null) return;if (left != null) {left.translateX(deltaX);}if (right != null) {right.translateX(deltaX);}}}private static class LevelInfo {int leftX;int rightX;public LevelInfo(Node left, Node right) {this.leftX = left.leftBound();this.rightX = right.rightBound();}}
}Printer
package redblacktree;public abstract class Printer {/*** 二叉树的基本信息*/protected BinaryTreeInfo tree;public Printer(BinaryTreeInfo tree) {this.tree = tree;}/*** 生成打印的字符串*/public abstract String printString();/*** 打印后换行*/public void println() {print();System.out.println();}/*** 打印*/public void print() {System.out.print(printString());}
}Strings
package redblacktree;public class Strings {public static String repeat(String string, int count) {if (string == null) return null;StringBuilder builder = new StringBuilder();while (count-- > 0) {builder.append(string);}return builder.toString();}public static String blank(int length) {if (length < 0) return null;if (length == 0) return "";return String.format("%" + length + "s", "");}
}总结
这个实现过程比较复杂,更多的是在提现一个打印结果的实现,没有必要自己去手敲,可以全部拿下来,去运行,看具体核心实现红黑树对应的那些功能。对于红黑树更细节的去使用,我也还在探索中,之后会更加细节的去记录。
ps:计划每日更新一篇博客,今日2023-05-04,日更第十八天。
昨日更新:
B树(B-tree、B-树)理论详解
相关文章:

红黑树理论详解与Java实现
文章目录 基本定义五大性质红黑树和2-3-4树的关系红黑树和2-3-4树各结点对应关系添加结点到红黑树注意事项添加的所有情况 添加导致不平衡叔父节点不是红色节点(祖父节点为红色)添加不平衡LL/RR添加不平衡LR/RL 叔父节点是红色节点(祖父节点为…...

container的讲解
我们做开发经常会遇到这样的一个需求,要开发一个响应式的网站,但是我们需要我们的元素样式跟随着我们的元素尺寸大小变化而变化。而我们常用的媒体查询(Media Queries)检测的是视窗的宽高,根本无法满足我们的业务需求&…...

JavaScript 箭头函数
(许多人所谓的成熟,不过是被习俗磨去了棱角,变得世故而实际了。那不是成熟,而是精神的早衰和个性的消亡。真正的成熟,应当是独特个性的形成,真实自我的发现,精神上的结果和丰收。——周国平&…...

简单理解Transformer注意力机制
这篇文章是对《动手深度学习》注意力机制部分的简单理解。 生物学中的注意力 生物学上的注意力有两种,一种是无意识的,零一种是有意识的。如下图1,由于红色的杯子比较突出,因此注意力不由自主指向了它。如下图2,由于…...

Vue3面试题:20道含答案和代码示例的练习题
Vue3中响应式数据的实现原理是什么? 答:Vue3中使用Proxy对象来实现响应式数据。当数据发生变化时,Proxy会自动触发更新。 const state {count: 0 }const reactiveState new Proxy(state, {set(target, key, value) {target[key] valueco…...

Oracle数据库创建用户
文章目录 1 查看当前连接的容器2 查看pdb下库的信息3 将连接改到XEPDB1下,并查看当前连接4 创建表空间5 创建用户6 用户赋权7 删除表空间、用户7.1 删除表空间7.2 删除用户 8 CDB与PDB的概念 1 查看当前连接的容器 SQL> show con_name;CON_NAME ---------------…...
)
互联网摸鱼日报(2023-04-30)
互联网摸鱼日报(2023-04-30) InfoQ 热门话题 被ChatGPT带火的大模型,如何实际在各行业落地? Service Mesh的未来在于网络 百度 Prometheus 大规模业务监控实战 软件技术栈商品化:应用优先的云服务如何改变游戏规则…...

第二章--第一节--什么是语言生成
一、什么是语言生成 1.1. 说明语言生成的概念及重要性 语言生成是指使用计算机程序来生成符合人类自然语言规范的文本的过程。它是自然语言处理(NLP)领域中的一个重要分支,涉及到语言学、计算机科学和人工智能等领域的交叉应用。语言生成技术可以被广泛地应用于自动问答系…...

HTML <!--...--> 标签
实例 HTML 注释: <!--这是一段注释。注释不会在浏览器中显示。--><p>这是一段普通的段落。</p>浏览器支持 元素ChromeIEFirefoxSafariOpera<!--...-->YesYesYesYesYes 所有浏览器都支持注释标签。 定义和用法 注释标签用于在源代码中…...

TinyML:使用 ChatGPT 和合成数据进行婴儿哭声检测
故事 TinyML 是机器学习的一个领域,专注于将人工智能的力量带给低功耗设备。该技术对于需要实时处理的应用程序特别有用。在机器学习领域,目前在定位和收集数据集方面存在挑战。然而,使用合成数据可以以一种既具有成本效益又具有适应性的方式训练 ML 模型,从而消除了对大量…...

JavaScript中的Concurrency并发:异步操作下的汉堡制作示例
这篇文章想讲一下JavaScript中同步与异步操作在一个简单的示例中的应用。我们将以制作汉堡为例,展示如何使用同步方法、回调函数(callbacks)和Promise与async/await来实现该过程。 Let’s imagine we’re trying to make a burger: 1. Get …...
微信小程序开发一个多少钱
小程序开发是当前比较流行的一项技术服务,能够为企业和个人带来巨大的商业价值和社会价值,但是小程序开发费用也是潜在的成本之一。在选择小程序开发服务时,了解开发费用如何计算、影响价格的因素以及如何降低成本等方面的知识,可…...

Python基础入门(2)—— 什么是控制语句、列表、元组和序列?
文章目录 01 | 🚄控制语句02 | 🚅列表03 | 🚈元组04 | 🚝序列05 | 🚞习题 A bold attempt is half success. 勇敢的尝试是成功的一半。 前面学习了Python的基本原则、变量、字符串、运算符和数据类型等知识,…...
计算机专业大一的一些学习规划建议!
大家好,我是小北。 五一嗖的一下就过啦~ 对于还在上学的同学五一一过基本上意味着这学期过半了,很多大一、大二的同学会有专业分流、转专业等事情。 尤其是大二的时候,你会发现身边有些同学都加入各种实验室了,有忙着打ACM、学生…...
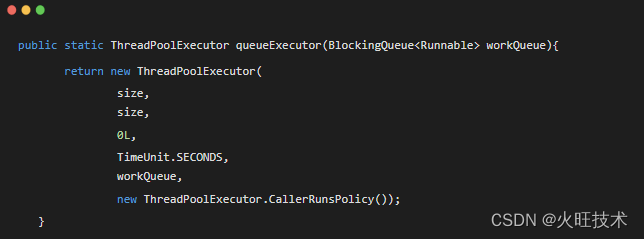
万万没想到在生产环境翻车了,之前以为很熟悉 CountDownLatch
前言 需求背景 具体实现 解决方案 总结 前言 之前我们分享了CountDownLatch的使用。这是一个用来控制并发流程的同步工具,主要作用是为了等待多个线程同时完成任务后,在进行主线程任务。然而,在生产环境中,我们万万没想到会…...

Springboot整合Jasypt实战
Springboot整合Jasypt实战 引入依赖 <dependency><groupId>com.github.ulisesbocchio</groupId><artifactId>jasypt-spring-boot-starter</artifactId><version>3.0.5</version> </dependency>配置jasypt # 配置jasypt相关信息…...
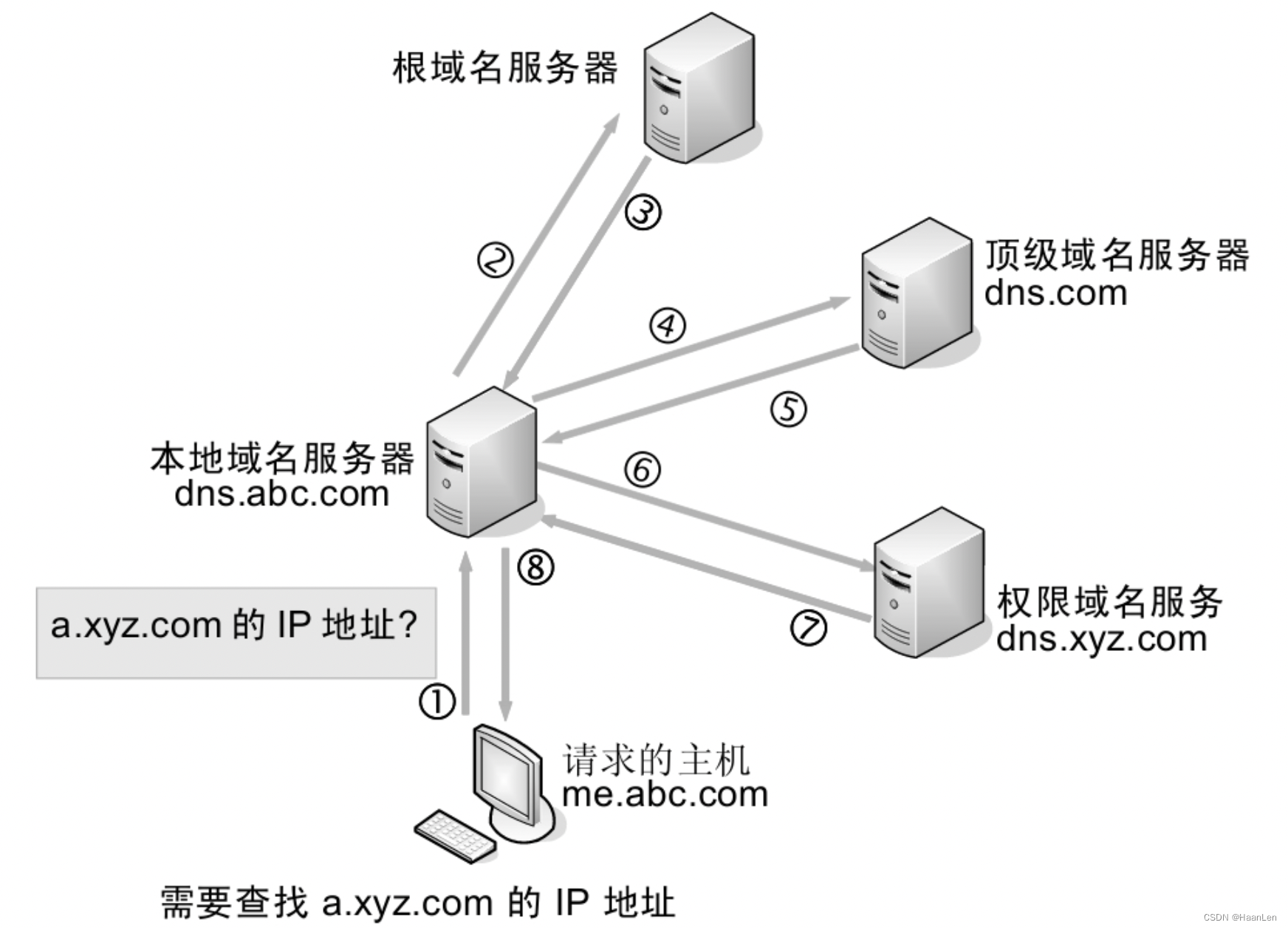
计算机网络笔记:DNS域名解析过程
基本概念 DNS是域名系统(Domain Name System)的缩写,也是TCP/IP网络中的一个协议。在Internet上域名与IP地址之间是一一对应的,域名虽然便于人们记忆,但计算机之间只能互相认识IP地址,域名和IP地址之间的转…...
C语言函数大全-- s 开头的函数(4)
C语言函数大全 本篇介绍C语言函数大全-- s 开头的函数(4) 1. strdup 1.1 函数说明 函数声明函数功能char * strdup(const char *s);用于将一个以 NULL 结尾的字符串复制到新分配的内存空间中 注意: strdup() 函数返回指向新分配的内存空间…...

Linux常见指令 (2)
Linux常见指令 ⑵ 补充man描述:用法:例子 echo描述:用法:例子 echo 字符串例子 echo 字符串 > 文件例子 追加重定向(>>)例子 输出重定向(>)来创建文件 && (>)来清空文件 cat描述:用法:例子 cat && cat 文件补充:例子 cat 文件 && cat &…...

shell脚本4
字符串变量 格式介绍:单引号 varabc 双引号 var"abc" 不使用引号 varabc 区别:单引号,原样输出,不会解析里面的变量 双引号,会解析变量,并且可以使用子双引号,需要转…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
