代码随想录算法训练营第四十九天| 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
文章目录
- 121. 买卖股票的最佳时机
- 122.买卖股票的最佳时机II
121. 买卖股票的最佳时机
为什么定义dp数组为二维数组?
dp数组定义,dp(i)[0] 表示第i天持有股票所得最多现金,dp(i)[1]表示第i天不持有股票的状态(未必当前卖出)
这样定义可以表示所有状态,否则dp[i]表示买入,那还要定义第i天卖出,和剩下两种状态持有和不持有
-
题目链接:代码随想录
-
解题思路:
①dp数组,dp(i)[0]表示第i天持有股票的最大现金,dp(i)[1]表示第i天不持有股票的最大现金
②递推公式 1.第i天
持有股票,可能第i天没买,最大现金为前一天持有股票的最大状态;有可能第i天买了,而且一定是第一次买,所以为-price[i]
2.第i天不持有股票**,可能是第i - 1天就不持有状态顺延;也有可能是正好这一天卖出股票,所以总现金为前一天持有状态 + 今天卖出状态
③初始化:
因为要用到i - 1状态,所以要有第0个元素
④遍历顺序:从前向后,因为后状态依赖前状态 -
推导过程
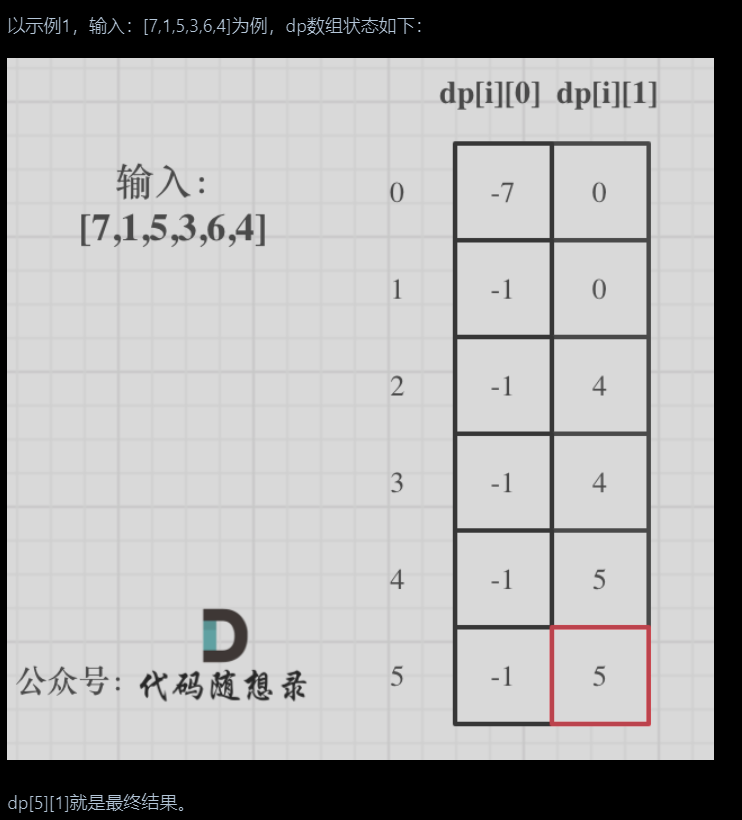
public int maxProfit(int[] prices) {//dp数组//dp[i][0]表示第i天持有股票的最大现金,dp[i][0]表示第i天不持有股票的最大现金int[][] dp = new int[prices.length][2];//初始化//因为i - 1所以,要有第0个元素dp[0][0] = -prices[0];dp[0][1] = 0;//遍历for (int i = 1; i < prices.length; i++) {//第i天持有股票,可能第i天没买,最大现金为前一天持有股票的最大状态;有可能第i天买了,而且一定是第一次买,所以为-price[i]dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);//第i天不持有股票,可能是第i - 1天就不持有状态顺延;也有可能是正好这一天卖出股票,所以总现金为前一天持有状态 + 今天卖出状态dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);}//一定是第i天不持有股票现金多,不持有一定现金更多return dp[prices.length - 1][1];
}
122.买卖股票的最佳时机II
本题和上一题唯一的区别在于:
当第i天持有并且第i天买入的情况,不再是单纯的-了,而是要算上前一天不持有的状态,因为可以买卖多次
而第i天不持有的情况和之前状态一样
- 题目链接:代码随想录
public int maxProfit(int[] prices) {//dp数组int[][] dp = new int[prices.length][2];//初始化dp[0][0] = -prices[0];dp[0][1] = 0;//遍历for (int i = 1; i < prices.length; i++) {//第i天持有股票,当第i天买入的时候,不再是单纯的-了,而是要算上前一天不持有的状态,因为可以买卖多次dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);//第i天不持有股票,状态和只能买卖一次的状态一样dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);}//一定是第i天不持有股票现金多,不持有一定现金更多return dp[prices.length - 1][1];
}
相关文章:

代码随想录算法训练营第四十九天| 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
文章目录 121. 买卖股票的最佳时机122.买卖股票的最佳时机II 121. 买卖股票的最佳时机 为什么定义dp数组为二维数组? dp数组定义,dp(i)[0] 表示第i天持有股票所得最多现金,dp(i)[1]表示第i天不持有股票的状态(未必当前卖出&#x…...

零基础如何学习挖漏洞?看这篇就够了【网络安全】
前言 有不少阅读过我文章的伙伴都知道,我从事网络安全行业已经好几年,积累了丰富的经验和技能。在这段时间里,我参与了多个实际项目的规划和实施,成功防范了各种网络攻击和漏洞利用,提高了安全防护水平。 也有很多小…...

Twitter 推荐算法底有多牛? 已斩获11.7K star
点击上方“Github中文社区”,关注 看Github,每天提升第070期分享 ,作者:Huber | Github中文社区 大家好,我是Huber。 在美国当地时间 3 月 31 日,马斯克履行当初的诺言,他宣布了 Twitter 算法的…...
看过这篇文章,读懂数据分析
一、为什么需要数据分析 数据分析的重要性不言而喻,没有数据,就是感性。数据不会被观点打败,数据只能被数据打败。我们现在妥妥地已经进入了数据时代。 量化IT投资成效,以数据驱动决策 站在公司或者决策者角度,数据最…...

[计算机图形学]光场,颜色与感知(前瞻预习/复习回顾)
一、Light Field / Lumigraph—光场 1.我们看到的是什么 我们的眼睛能够把3D世界转换为2D的成像信号被我们感知,如上面第一幅图,这就是我们看到整个世界的过程,那么如果我们把之前记录的光的信息都完美的放在一个幕布上,那么我们…...

L4公司进军辅助驾驶,放话无图也能跑遍中国
作者 | Amy 编辑 | 德新 高阶智能驾驶走向规模量产,高精地图成为关键的门槛之一。今年,多家车企和智驾公司都喊出「不依赖高精地图,快速大规模落地」的口号。 华为、小鹏、元戎以及毫末等,可能是最快在国内量产 无高精图智…...

【Java笔试强训 17】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥杨辉三角…...
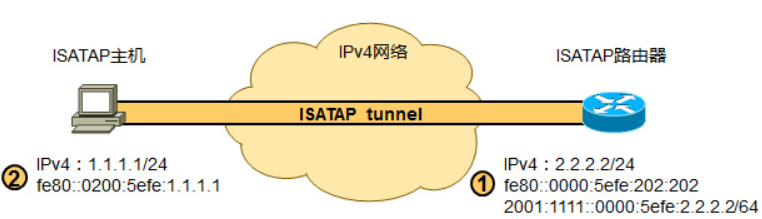
【IPv6】基本概念及字段
IPV4知识点: 字段值 IPv4字段共 字段值解释Version版本版本字段,可以区分V4和V6版本,V4是0100,V6是0110,需要注意的是V4和V6头部除了版本字段位置相同外,其他都是不一样的,因此两个协议不能直…...

数据库中的 Schema 变更实现
线上沙龙-技术流第 30 期营业啦 05月09日(周二)19:30 KaiwuDB - B站直播间 传统数据库操作 Schema 变更时,第一步便是锁表,需持续到 Schema 变更操作完成。这样的做法虽然实现简单,无需考虑事务并发带来的影响&#…...

【C++ 学习 ②】- 类和对象(上)
目录 一、 面向对象的基本理念 1.1 - 什么是对象? 1.2 - 类和对象 1.3 - 面向对象的五条原则 1.4 - 面向过程 vs 面向对象 二、C 中的结构体 三、类的定义 3.1 - 类的两种定义方式 3.2 - 成员变量的命名规范 四、类的访问限定符和封装 4.1 - 访问限定符 …...

最好的物联网教程:软硬结合——从零打造物联网
在大学里不同专业有着不同的追求:机械类与强电类专业学生追求的是 “机电合一” ,既懂机械又懂电气,整个电气机械自动化便能打通。弱电类专业学生追求的是 “软硬结合” ,既懂硬件又懂软件,整个电子产品便能打通。我作…...

猫狗训练集训练报错:Failed to find data adapter that can handle input
这里写自定义目录标题 Jupyter Notebook6.5.4 tensorflow 2.12.0 pillow 9.5.0 numpy 1.23.5 keras 2.12.0 报错详细内容: ValueError: Failed to find data adapter that can handle input: (<class ‘tuple’> containing values of types {“<class ‘k…...
中国网络安全人才需求
如果你是一个想要入门网络安全行业的小白、如果你是网络安全专业在读的大学生、如果你是正在找工作的新手,那么这篇文章你一定要仔细看。毕竟知己知彼百战百胜,知道行业的人才需求才能更好得发挥自己的优势。 当你打开BOSS直聘、拉钩等招聘网站…...

设计模式之组合模式
目录 1、组合模式的定义 2、组合模式例子 3、组合模式实现 3.1 组合模式的结构 3.2 组合模式的分类 3.3 组合模式代码实现(透明组合模式) 4、组合模式的优点 5、组合模式使用场景 1、组合模式的定义 组合模式又名部分整体模式,是用于把…...
计算机基础书籍
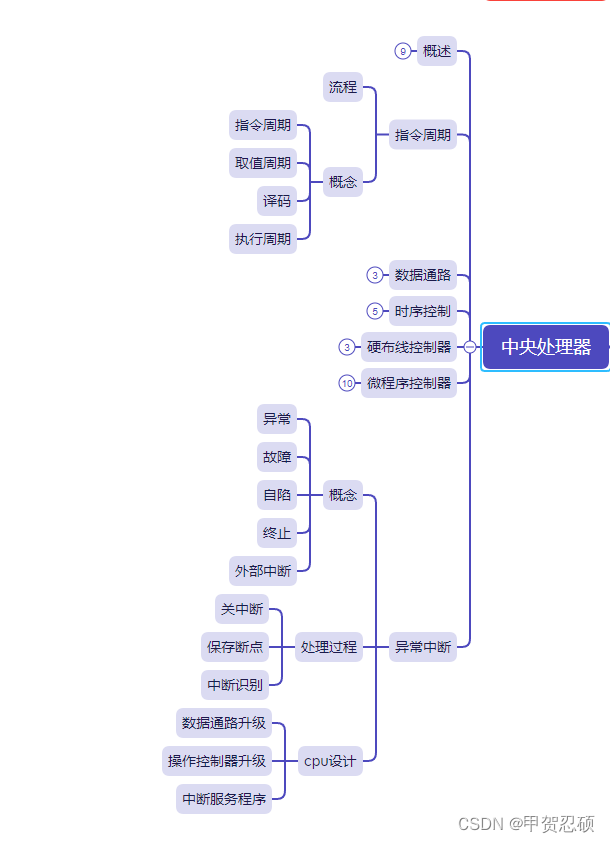
一操作系统 二常见问题总结 1.操作系统的特征? 并发、共享、虚拟、异步性 2.进程阻塞与唤醒的条件 等待 I/O 操作完成请求系统资源失败等待信号量或事件等待子进程结束被高优先级进程抢占 3.如何避免死锁? 1、避免资源竞争 2、破坏循环等待条件 3、优…...

保龄球游戏的获胜者、找出叠涂元素----2023/4/30
保龄球游戏的获胜者----2023/4/30 给你两个下标从 0 开始的整数数组 player1 和 player2 ,分别表示玩家 1 和玩家 2 击中的瓶数。 保龄球比赛由 n 轮组成,每轮的瓶数恰好为 10 。 假设玩家在第 i 轮中击中 xi 个瓶子。玩家第 i 轮的价值为: …...

jQuery事件
1. jQuery事件注册 单个事件注册 语法: element.事件(function(){}) eg:$(“div”).click(function(){ 事件处理程序 }) 其他事件和原生基本一致。比如mouseover、mouseout、blur、focus、change、keydown、keyup、resize、scroll 等 <!DOCTYP…...
初识SpringCloud
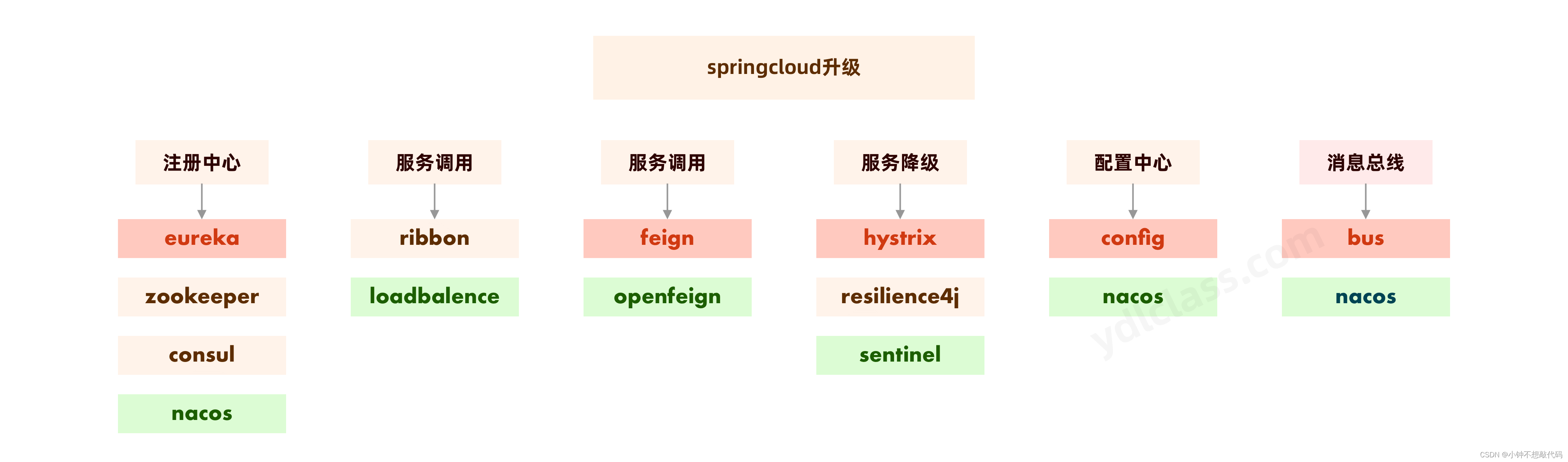
一、软件架构演进 单体架构 垂直架构 分布式架构 SOA架构 微服务架构 二、微服务架构 2.1 微服务理念 "微服务”一词源 于 Martin Fowler的名为 Microservices的博文,可以在他的官方博客上找到http://martinfowler.com/articles/microservices.html微服务是系统架构上…...

安装java配置
目录 安装JDK 编辑 环境变量配置 3、检验环境变量配置 二、安装tomcat 验证Tomcat配置是否成功 三、安装Mysql 一、安装 二、卸载 四、安装Maven 安装JDK 点击更改将C直接给为F即可。 点击确定后进行安装,安装完以后会提示安装JRE; 检测是否已经安装JDK的…...

KBO的选秀会有哪些规定和流程`棒球7号位
KBO(韩国职业棒球联盟)的选秀会有以下规定和流程: 1. 选秀对象:KBO的选秀会主要面向年满18岁及以上的高中和大学生,以及海外球员和自由球员。KBO的球队可以在选秀会中挑选所需的球员,每个球队有一定数量的选…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
