洛谷 子集积 题解
题目
P1 背包
子集积 > m >m >m 个数并不好求,考虑子集积 ≤ m \le m ≤m 的个数 x x x,答案即为 ( 2 n − x ) (2^n - x) (2n−x)。
对于子集积 ≤ m \le m ≤m 的个数,可以化为 0-1 背包问题做, f i , j f_{i,j} fi,j 表示前 i i i 个数,子集积为 j j j 的个数,有:
f i , j = ∑ j = 1 m f i − 1 , j a i f_{i,j}=\sum \limits_{j=1}^{m} f_{i-1,\frac {j} {a_i}} fi,j=j=1∑mfi−1,aij ( j j j 是 a i a_i ai 的倍数)。
背包问题常规地去掉一维: f j f_j fj 表示子集积为 j j j 的个数:
f j = ∑ j = 1 m f j a i f_j=\sum \limits_{j=1}^{m} f_{\frac {j} {a_i}} fj=j=1∑mfaij ( j j j 是 a i a_i ai 的倍数)。
cin >> n >> m;for(int i=1; i<=n; i++) cin >> a[i];f[1] = 1;for(int i=1; i<=n; i++)for(int j=(m / a[i]) * a[i]; j>=a[i]; j-=a[i])f[j] += f[j / a[i]], f[j] %= mod;int sum = qpow(2, n);for(int i=1; i<=m; i++)sum -= f[i], sum = ((sum % mod) + mod) % mod;cout << sum;
时间复杂度 O ( n × ∑ i = 1 n m a i ) O(n \times \sum\limits_{i=1}^{n} {\frac {m} {a_i}}) O(n×i=1∑naim) ,最坏情况下 O ( n m ) O(nm) O(nm) 。
P2 优化
优化 1
若序列中有 100 100 100 个 1 1 1 ,然而任意多个 1 1 1 不会对子集积产生影响,我们只需要在方案数中乘以 2 100 2^{100} 2100 即可。
...int sum = qpow(2, n);for(int i=1; i<=m; i++)sum -= (f[i] * qpow(2, cnt[1])) % mod, sum = ((sum % mod) + mod) % mod;cout << sum;
优化 2
时间复杂度高的原因在于重复的计算:若有 100 100 100 个 2 2 2 ,我们会将第 2 , 3 2,3 2,3 个 2 2 2 、第 3 , 4 3,4 3,4 个 2 2 2 算了两次。我们应该只关心是几个 2 2 2 ,而不关心是哪几个 2 2 2。
对于任意一个数 x x x ,设其出现了 t t t 次,我们可以对 x 1 , x 2 , . . . , x t x^1,x^2,...,x^t x1,x2,...,xt 分别计算,使用 x i x^i xi 计算贡献时乘以 C t i C_{t}^i Cti, 即 :
f j = ∑ i = 1 t ( f j x i × C t i ) f_j=\sum\limits_{i=1}^{t} ( f_{\frac {j} {x^i}} \times C_t^i) fj=i=1∑t(fxij×Cti) ( j j j 是 x k x^k xk 的倍数)。
时间复杂度 O ( n ∑ i = 1 n ( log a i m ) ) O(n \sum\limits_{i=1}^{n} (\log_{a_i}{m})) O(ni=1∑n(logaim)),最坏情况下 O ( n log m ) O(n \log m) O(nlogm)。
注意: 这里与多重背包的二进制拆分拆成多个物品不同,而是优化了对于一个物品的计算方式。
代码
相关文章:

洛谷 子集积 题解
题目 P1 背包 子集积 > m >m >m 个数并不好求,考虑子集积 ≤ m \le m ≤m 的个数 x x x,答案即为 ( 2 n − x ) (2^n - x) (2n−x)。 对于子集积 ≤ m \le m ≤m 的个数,可以化为 0-1 背包问题做, f i , j f_{i,…...

Boost笔记 1:下载、编译、安装、测试
1. 下载 当前版本是1.82,下载链接: https://boostorg.jfrog.io/artifactory/main/release/1.82.0/source/ 2. 安装编译依赖库 本地环境是Ubuntu 22.04,需要安装以下依赖库,部分影响boost相关功能的开启,部分影响编译…...

tiechui_lesson01_入口函数和卸载函数
主要讲解入口函数和卸载函数。 #include <ntifs.h>VOID nothing(HANDLE ppid, HANDLE mypid, BOOLEAN bcreate) {UNREFERENCED_PARAMETER(ppid);UNREFERENCED_PARAMETER(mypid);UNREFERENCED_PARAMETER(bcreate);DbgPrint("processNotify\n"); }VOID DriverU…...

密码学【java】初探究加密方式之非对称加密
文章目录 非对称加密1 常见算法2 生成公钥和私钥3 私钥加密4 私钥加密 公钥解密5 公钥和私钥的保存和读取5.1 **保存公钥和私钥**5.2 读取公钥和私钥 非对称加密 非对称加密算法又称现代加密算法。非对称加密是计算机通信安全的基石,保证了加密数据不会被破解。与对…...

网络安全和黑客技能:15本必读书籍推荐
前言 网络安全和黑客技能紧密相连。想要有效地防范黑客攻击,了解黑客的技能和思维方式非常重要。而要想成为一名合格的白帽黑客,也需要深入理解网络安全的基本原理和最佳实践。本文将介绍15本网络安全和黑客书籍,既包括了防范黑客攻击的指南…...

电话号码的字母组合
题目:17. 电话号码的字母组合 - 力扣(Leetcode) 思路: 给定一个电话号码字符串 digits,须输出它所能表示的所有字母组合。我们可以先定义一个数字字符到字母表的映射表 numToStr,然后再用 Combine 函数递归…...
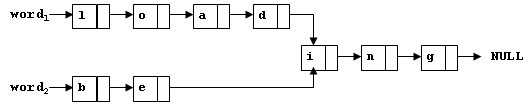
PAT A1032 Sharing
1032 Sharing 分数 25 作者 CHEN, Yue 单位 浙江大学 To store English words, one method is to use linked lists and store a word letter by letter. To save some space, we may let the words share the same sublist if they share the same suffix. For example, l…...

Git常见问题汇总
问题:Your branch is ahead of ‘origin/master’ by 1 commit 原因:你的本地分支高于远程仓库一次提交, 同步更新下,执行命令: git push origin master问题:warning: LF will be replaced by CRLF in main.lua The …...

设计模式之代理模式(静态代理动态代理)
目录 1、什么是代理模式 2、代理模式的结构 3、代理模式的实现 3.1 静态代理和动态代理概念 3.2 静态代理 3.3 动态搭理 3.3.1 代码实现 3.3.2 Proxy类讲解 4、动态代理VS静态代理 5、代理模式优缺点 1、什么是代理模式 由于某些原因需要给某对象提供一个代理以控制对…...

Java并发编程基础知识概述
前言 在现代计算机系统和服务器中,多线程并行执行已经成为常态,而且并发编程能够充分利用系统资源,提高程序处理效率和质量。因此,Java并发编程是Java程序员必须掌握的重要技能之一。 线程和进程 在操作系统中,进程是…...
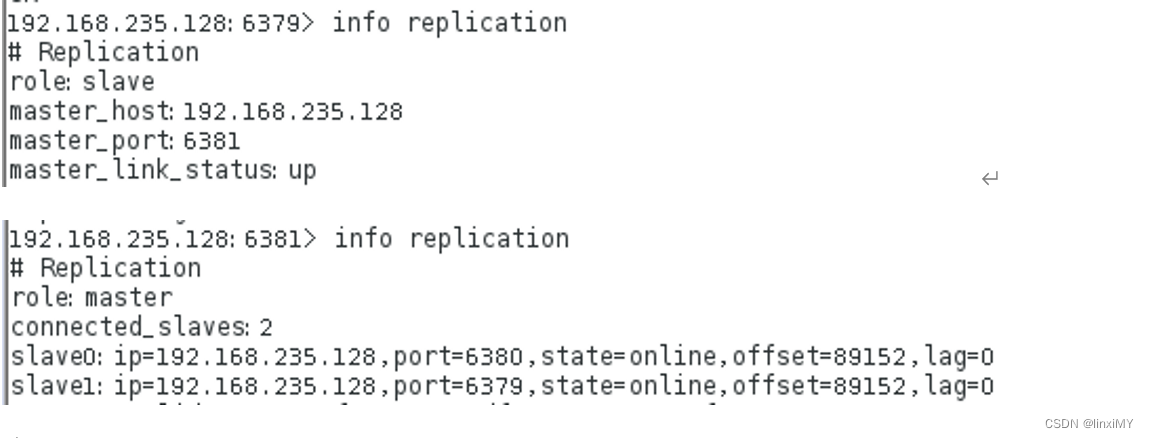
Redis超详细入门手册教程!还不快来看看?
地址: RedisRedis is an open source (BSD licensed), in-memory data structure store, used as a database, cache, and message broker. Redis provides data structures …https://redis.io/ 1:NoSQL简介 1.1:数据库应用的演变历程 单…...
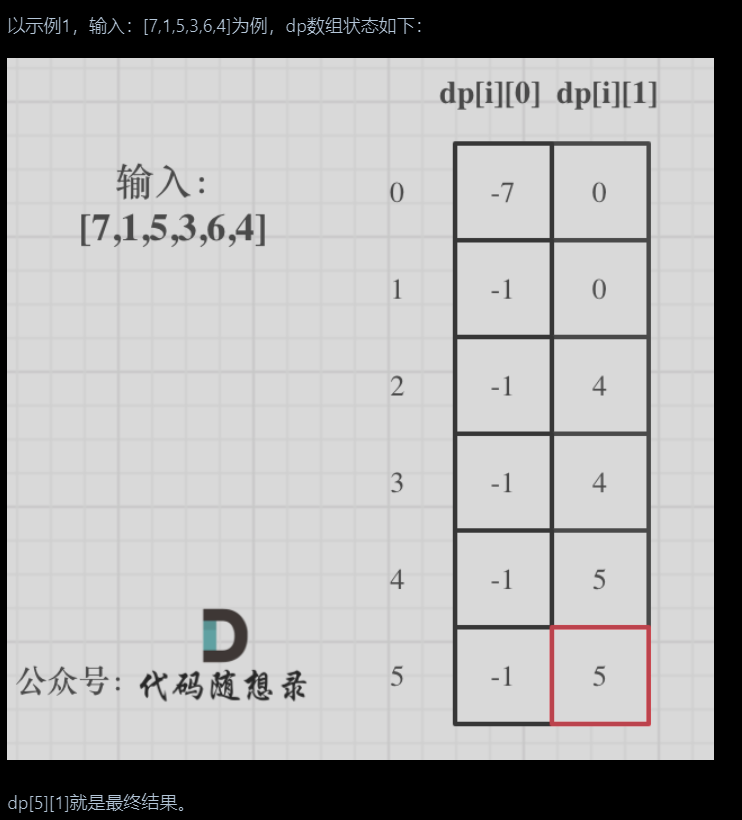
代码随想录算法训练营第四十九天| 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
文章目录 121. 买卖股票的最佳时机122.买卖股票的最佳时机II 121. 买卖股票的最佳时机 为什么定义dp数组为二维数组? dp数组定义,dp(i)[0] 表示第i天持有股票所得最多现金,dp(i)[1]表示第i天不持有股票的状态(未必当前卖出&#x…...

零基础如何学习挖漏洞?看这篇就够了【网络安全】
前言 有不少阅读过我文章的伙伴都知道,我从事网络安全行业已经好几年,积累了丰富的经验和技能。在这段时间里,我参与了多个实际项目的规划和实施,成功防范了各种网络攻击和漏洞利用,提高了安全防护水平。 也有很多小…...

Twitter 推荐算法底有多牛? 已斩获11.7K star
点击上方“Github中文社区”,关注 看Github,每天提升第070期分享 ,作者:Huber | Github中文社区 大家好,我是Huber。 在美国当地时间 3 月 31 日,马斯克履行当初的诺言,他宣布了 Twitter 算法的…...
看过这篇文章,读懂数据分析
一、为什么需要数据分析 数据分析的重要性不言而喻,没有数据,就是感性。数据不会被观点打败,数据只能被数据打败。我们现在妥妥地已经进入了数据时代。 量化IT投资成效,以数据驱动决策 站在公司或者决策者角度,数据最…...

[计算机图形学]光场,颜色与感知(前瞻预习/复习回顾)
一、Light Field / Lumigraph—光场 1.我们看到的是什么 我们的眼睛能够把3D世界转换为2D的成像信号被我们感知,如上面第一幅图,这就是我们看到整个世界的过程,那么如果我们把之前记录的光的信息都完美的放在一个幕布上,那么我们…...

L4公司进军辅助驾驶,放话无图也能跑遍中国
作者 | Amy 编辑 | 德新 高阶智能驾驶走向规模量产,高精地图成为关键的门槛之一。今年,多家车企和智驾公司都喊出「不依赖高精地图,快速大规模落地」的口号。 华为、小鹏、元戎以及毫末等,可能是最快在国内量产 无高精图智…...

【Java笔试强训 17】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥杨辉三角…...
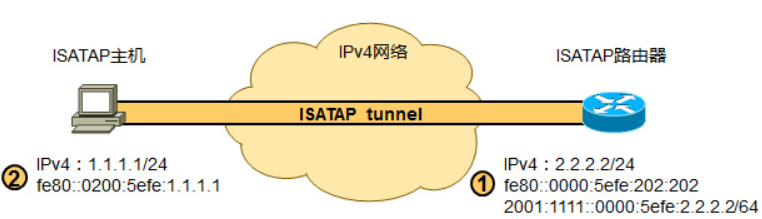
【IPv6】基本概念及字段
IPV4知识点: 字段值 IPv4字段共 字段值解释Version版本版本字段,可以区分V4和V6版本,V4是0100,V6是0110,需要注意的是V4和V6头部除了版本字段位置相同外,其他都是不一样的,因此两个协议不能直…...

数据库中的 Schema 变更实现
线上沙龙-技术流第 30 期营业啦 05月09日(周二)19:30 KaiwuDB - B站直播间 传统数据库操作 Schema 变更时,第一步便是锁表,需持续到 Schema 变更操作完成。这样的做法虽然实现简单,无需考虑事务并发带来的影响&#…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
