【博弈论】【第一章】博弈论导论
博弈论导论
- 【例题】选择数字
- 【例题】巴什博弈
- 【例题】射手博弈
- 博弈论的基本概念:
- 参与人
- 战略
- 行动
- 信息
- 支付函数
- 【例题】分100元
课程概述:

【例题】选择数字
两个参与人A和B,轮流选择[3,4,5,6,7,8,9]中的一个整数(可重复)。当累计总和达到100的时候,博弈结束。此时判所选数字恰好使累计总和达到或超过100的参与人为输家。试问最先行动的A能赢得这场博弈吗?最优策略又是什么?
【解】
整个游戏的过程:

如果前面选择的数字之和能够达到97,98,99的话,那么下一个人最少选择的是3,所以就一定会等于或者超过100。那么这个人就输了。

所以我们如何去控制A每一轮的选择,使得最后一轮该B选择的时候,数字加和已经到达97,98,99,从而使得B一定输呢?
那就是找到每一轮我们可以控制的数。
由于我们观察到我么可选择的数的范围中,两个人选择的数字加和最大是12,也就是我们总可以通过不同的数字组合控制每一轮的加和达到固定的数字12。那么就可以一轮一轮往前推,推到第一轮A应该先手选择什么数字能赢。所以大致思路就是这样的:
据逆推归纳法,当累计接近100时,得到99的A会赢,问题变为抢99。同理,问题可变为抢87[=99-(3+9)],75,63,51,39,27,15,3,继续逆推,就是先抢到3,会赢。A先选3,则A胜出。
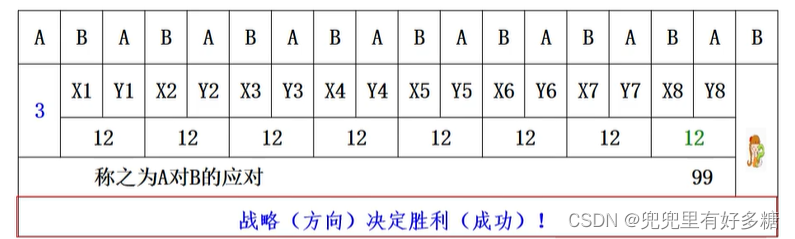
但是如果我们不用上面的战略,第一轮的时候A选择4呢?
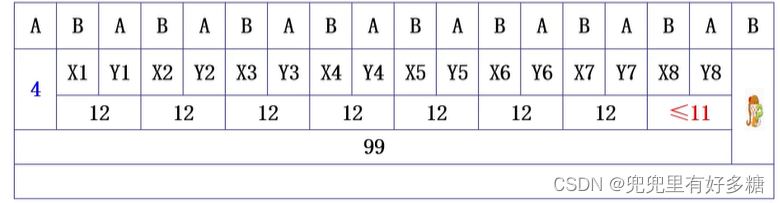
那么一定会导致最后一轮的时候A于B的加和必须小于11,然后轮到B的时候才能是99。但是这是不可控制的,因为一但B选择9,A不论选择什么,这个加和都不可能小于11,所以A直接输掉比赛了。
所以有如下命题:
【命题1】在数字游戏1中,先行动者存在唯一的必胜的最佳应对战略(策略)。
考虑反应对的情形:在本示例中,我们采取的是当A=3时,B选择X1,A再选择Y1,使得X1+Y1=12(我们把这种情形称之为A对B的应对),进而A能保证赢。如果当A=3时(同学们也可以试试开始时A为其他数字的情形,情况可能有些复杂),B采取A+X1=12,依次Y1+X2=12,…,我们把这种情形称之为B对A的反应对。
但是如果先行动者第一局选择的3,后面都采用和为12的策略,那么B不论做何反应对都是没有用的,B面临的是必输的局面。
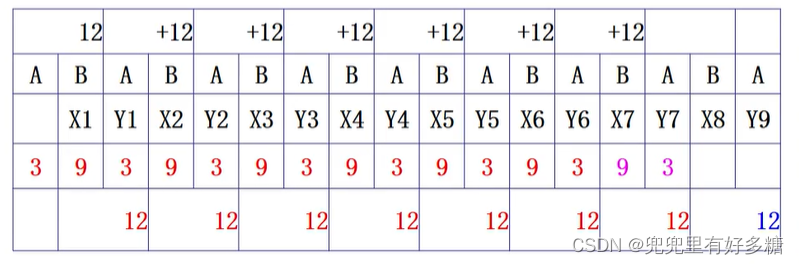
但是如果A一开始没有选择3,而选择的是其他数字,那么B用反应对策略都有唯一的一个机会取胜。
如下图所示,A第一局没有选择3,那么他只能选择比3大的数字,然后B把第一局的加和控制为13,而后面每一局B都使得加和为12,则总和为12*6+13=85。那么在最后一局的时候B只要控制加和为12就是必胜,并且根据A的选择,也可以控制为13或者14,都是必胜的策略。
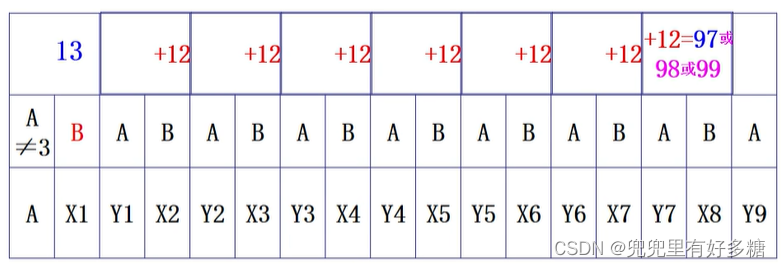
因此又有如下命题:
【命题2】在数字游戏1中,先行动者若开始选择的数字A≠3,则后行动者存在必胜的最佳应对战略(策略),且针对每个不等于3的A,这个战略(策略)是唯一的。
如果达到或超过100的参与人为赢家,局势会怎么样呢?
根据逆推归纳法,当累计接近100时,得到88的人会赢,问题变为抢88。同理,问题可变为抢76,64,52,40,28,16,4,继续逆推(
100-12n,当n=8时余4),就是先抢到4的人会赢。先行动的A先选4,则A胜出。
【例题】巴什博弈
一堆石子有n颗,A、B两个人轮流拿取,每次至少拿取1颗,至多拿取m颗,拿走最后一颗石子的人获胜。
【解】
假设石子有 n=m+1由于一次只能取m颗,无论先手取多少颗,后手总能拿走剩余的,这时一定是先手负。
若石子n= (m+1)*r+s,对于先手应该先取走s颗,设后手取走k颗,先手再取走m+1-k,剩余的石子颗数为(m+1)(r-1)以后保持这样的取法,先取者获胜。总之,就是要留给对手m+1的倍数。
【命题3】在巴什博弈中,如果石子数量n%(m + 1)=0 时,后手胜;如果石子数量n%(m + 1)≠0时,先手胜。
【例题】射手博弈
射手A、B、C以抽签的方式决定轮流开枪的顺序并进行决斗,A的命中率为100%,B的命中率为80%,C的命中率为50%。
(1)若按顺序进行且C首先开枪射击,他应该怎样做?
(2)如果按顺序进行射击,证明C存活的可能性最大。
(3)若每一轮开枪的人是任意选择的,证明射手存活的概率与命中率完全相反
【解】
追求的目标一定是两个:首先是考虑保命,然后再考虑射击谁。
(1)若按顺序进行且C首先开枪射击,他应该怎样做?
设 π A ( A B C ) \pi_A(ABC) πA(ABC)表示三人都活着,且按ABC顺序射击时A存活的概率,其余表示含义类似。
①如果C射击其他人,一定是射击A。(因为首先要考虑保命,所以一定会优先射击那个命中率高的人)
如果C击中A,那么他的支付为 π C ( B C ) \pi_C(BC) πC(BC)。
因为在BC这个顺序下C存活的概率取决于B的命中率,如果B把C打中了,那么C存活概率就是0,打所以这种情况下C的存活概率是 4 5 ∗ 0 = 0 \frac{4}{5}*0=0 54∗0=0,如果没有打中的话(概率是 1 5 \frac{1}{5} 51),就该C打B了。
所以有式子: π C ( B C ) = π C ( C B ) / 5 \pi_C(BC)=\pi_C(CB)/5 πC(BC)=πC(CB)/5
而 π C ( C B ) = 1 2 × 1 + 1 2 × π C ( B C ) = 1 2 × 1 + 1 2 × 1 5 π C ( C B ) \pi_C(C B)=\frac{1}{2} \times 1+\frac{1}{2} \times \pi_C(B C)=\frac{1}{2} \times 1+\frac{1}{2} \times \frac{1}{5} \pi_C(C B) πC(CB)=21×1+21×πC(BC)=21×1+21×51πC(CB)
于是可得:
π C ( C B ) = 5 9 , π C ( B C ) = 1 9 ( C 击中 A , C 存活的概率 ) \pi_C(C B)=\frac{5}{9}, \pi_C(B C)=\frac{1}{9} (C击中A,C存活的概率) πC(CB)=95,πC(BC)=91(C击中A,C存活的概率)
没有击中A的情况如②:
②如果C射向空中。显然A将射向B而不是C,并且B将会射向A而不是C。(因为首先要考虑保命,所以一定会优先射击那个命中率高的人)。因而A和B将会互相射击,直到其中一个人出局,接着该轮到C射击了。
若A是A、B互相射击的幸存者,则此时C幸存的概率为 π C ( C A ) = 1 2 \pi_C(CA)=\frac{1}{2} πC(CA)=21。
若B是A、B互相射击的幸存者,则此时C幸存的概率是 π C ( C B ) = 5 9 \pi_C(CB)=\frac{5}{9} πC(CB)=95。
因为 π C ( C B ) = 5 9 \pi_C(CB)=\frac{5}{9} πC(CB)=95, π C ( C A ) = 1 2 \pi_C(CA)=\frac{1}{2} πC(CA)=21,均大于 π C ( B C ) = 1 9 \pi_C(BC)=\frac{1}{9} πC(BC)=91。所以C射向空中是其最优选择。
(2)如果按顺序进行射击,证明C存活的可能性最大。
证明:①假设A在B之前射击,顺序可能为CAB或ACB或ABC三种可能。
因为C射向空中,A一定确保能干掉B,所以
π C ( C A B ) = π C ( A C B ) = π C ( A B C ) = 1 2 \pi_C(C A B)=\pi_C(A C B)=\pi_C(A B C)=\frac{1}{2} πC(CAB)=πC(ACB)=πC(ABC)=21
于是可得:
π A ( C A B ) = π A ( A C B ) = π A ( A B C ) = 1 2 \pi_A(C A B)=\pi_A(A C B)=\pi_A(A B C)=\frac{1}{2} πA(CAB)=πA(ACB)=πA(ABC)=21
②假设B在A之前射击,顺序为CBA或BCA或BAC三种可能。那么B就会射向A,击中的概率为4/5,因而
π C ( C B A ) = π C ( B C A ) = π C ( B A C ) = 4 5 π C ( C B ) + 1 5 π C ( C A ) = 4 5 × 5 9 + 1 5 × 1 2 = 49 90 \begin{aligned} \pi_C(C B A) & =\pi_C(B C A)=\pi_C(B A C) \\ & =\frac{4}{5} \pi_C(C B)+\frac{1}{5} \pi_C(C A) \\ & =\frac{4}{5} \times \frac{5}{9}+\frac{1}{5} \times \frac{1}{2}=\frac{49}{90} \end{aligned} πC(CBA)=πC(BCA)=πC(BAC)=54πC(CB)+51πC(CA)=54×95+51×21=9049
此外
π A ( C B A ) = π A ( B C A ) = π A ( B A C ) = 4 5 × 0 + 1 5 × 1 2 = 1 10 π B ( C B A ) = 4 5 × 4 9 + 1 5 × 0 = 16 45 \begin{aligned} \pi_A(C B A)=\pi_A(B C A)=\pi_A(B A C)\\ =\frac{4}{5} \times 0+\frac{1}{5} \times \frac{1}{2}=\frac{1}{10} \\ \pi_B(C B A) & =\frac{4}{5} \times \frac{4}{9}+\frac{1}{5} \times 0=\frac{16}{45} \end{aligned} πA(CBA)=πA(BCA)=πA(BAC)=54×0+51×21=101πB(CBA)=54×94+51×0=4516
(3)若每一轮开枪的人是任意选择的,证明存活率与命中率完全相反。
【证明】设 π A [ A ] \pi_A[A] πA[A]表示A开第一枪时A幸存概率, π A \pi_A πA表示A总体幸存概率, π A { A B } \pi_A\left\{AB\right\} πA{AB}表示AB两人谁开第一枪是任意的。其余类似表示。
如果下一轮进行射击的选手任意选择,结果依然是A和B将会互相射击直到两人中只有一人幸存。无论如何,显然C更愿意与B一对一较量而不是与A,所以C有机会射击的话将会射向A。
现在分析两个人的情形:
π A { A B } = 1 2 × 1 + 1 2 × 1 5 π A { A B } π A { A B } = 5 9 , π B { A B } = 4 9 \begin{aligned} & \pi_A\{A B\}=\frac{1}{2} \times 1+\frac{1}{2} \times \frac{1}{5} \pi_A\{A B\} \\ & \pi_A\{A B\}=\frac{5}{9}, \quad \pi_B\{A B\}=\frac{4}{9} \end{aligned} πA{AB}=21×1+21×51πA{AB}πA{AB}=95,πB{AB}=94
以此类推:
π A { A C } = 1 2 × 1 + 1 2 × ( 1 2 × π A { A C } ) \pi_A\{A C\}=\frac{1}{2} \times 1+\frac{1}{2} \times\left(\frac{1}{2} \times \pi_A\{A C\}\right) πA{AC}=21×1+21×(21×πA{AC})
于是有 π A { A C } = 2 3 , π C { A C } = 1 3 \pi_A\{A C\}=\frac{2}{3}, \pi_C\{A C\}=\frac{1}{3} πA{AC}=32,πC{AC}=31
进而有:
π B { B C } = 1 2 × [ 4 5 × 1 + 1 5 π B { B C } ] + 1 2 × 1 2 π B { B C } \pi_B\{B C\}=\frac{1}{2} \times\left[\frac{4}{5} \times 1+\frac{1}{5} \pi_B\{B C\}\right]+\frac{1}{2} \times \frac{1}{2} \pi_B\{B C\} πB{BC}=21×[54×1+51πB{BC}]+21×21πB{BC}
π B { B C } = 8 13 π C { B C } = 5 13 \begin{aligned} & \pi_B\{B C\}=\frac{8}{13} \\ & \pi_C\{B C\}=\frac{5}{13} \end{aligned} πB{BC}=138πC{BC}=135
现在,显然:
π A [ A ] = π A { A C } = 2 3 , π B [ A ] = 0 , π C [ A ] = 1 3 \pi_A[A]=\pi_A\{A C\}=\frac{2}{3}, \pi_B[A]=0, \pi_C[A]=\frac{1}{3} πA[A]=πA{AC}=32,πB[A]=0,πC[A]=31
同样, 容易得到
π B [ B ] = 4 5 π B { B C } + 1 5 π B , π A [ B ] = 1 5 π A π C [ B ] = 4 5 π C { B C } + 1 5 π C 和 π C [ C ] = 1 2 π C { B C } + 1 2 π C , π A [ C ] = 1 2 π A π B [ C ] = 1 2 π B { B C } + 1 2 π B \begin{aligned} & \pi_B[B]=\frac{4}{5} \pi_B\{B C\}+\frac{1}{5} \pi_B, \pi_A[B]=\frac{1}{5} \pi_A \\ & \pi_C[B]=\frac{4}{5} \pi_C\{B C\}+\frac{1}{5} \pi_C \\ & \text { 和 } \pi_C[C]=\frac{1}{2} \pi_C\{B C\}+\frac{1}{2} \pi_C, \pi_A[C]=\frac{1}{2} \pi_A \\ & \pi_B[C]=\frac{1}{2} \pi_B\{B C\}+\frac{1}{2} \pi_B \end{aligned} πB[B]=54πB{BC}+51πB,πA[B]=51πAπC[B]=54πC{BC}+51πC 和 πC[C]=21πC{BC}+21πC,πA[C]=21πAπB[C]=21πB{BC}+21πB
合并到一起计算,于是得到:
π A = 1 3 [ 2 3 + 1 5 π A + 1 2 π A ] → π A = 20 69 π B = 1 3 [ 0 + 4 5 π B { B C } + 1 5 π B + 1 2 π B { B C } + 1 2 π B ] → π B = 24 69 π C = 1 3 [ 1 3 + 4 5 π C { B C } + 1 5 π C + 1 2 π C { B C } + 1 2 π C ] → π C = 25 69 \begin{aligned} & \pi_A=\frac{1}{3}\left[\frac{2}{3}+\frac{1}{5} \pi_A+\frac{1}{2} \pi_A\right] \rightarrow \pi_A=\frac{20}{69} \\ & \pi_B=\frac{1}{3}\left[0+\frac{4}{5} \pi_B\{B C\}+\frac{1}{5} \pi_B+\frac{1}{2} \pi_B\{B C\}+\frac{1}{2} \pi_B\right] \rightarrow \pi_B=\frac{24}{69} \\ & \pi_C=\frac{1}{3}\left[\frac{1}{3}+\frac{4}{5} \pi_C\{B C\}+\frac{1}{5} \pi_C+\frac{1}{2} \pi_C\{B C\}+\frac{1}{2} \pi_C\right] \rightarrow \pi_C=\frac{25}{69} \end{aligned} πA=31[32+51πA+21πA]→πA=6920πB=31[0+54πB{BC}+51πB+21πB{BC}+21πB]→πB=6924πC=31[31+54πC{BC}+51πC+21πC{BC}+21πC]→πC=6925
于是有
π C > π B > π A \pi_C>\pi_B>\pi_A πC>πB>πA
得证。
(视频是2.23第一节)
博弈论的基本概念:
博弈论的基本概念:参与人、战略、行动、信息、支付函数、均衡结果等。
- 要素(PAPI):博弈主体(参与人)、战略(行动)、支付、信息。
- 规则:参与人、行动次序、均衡结果。
参与人
独立决策、独立行动并承担结果的个人或组织。
“自然”:“虚拟参与人”
根据参与人数分:
- 单人博弈
- 两人博弈
- 多人博弈
战略
行动
信息
支付函数
【例题】分100元
两个人各报一个至多为100的非负整数。若所报的数字之和不超过100,则每人得到所报的钱数(多余的钱充公)﹔若两人所报的数字之和超过100且数目不同,则报较小数的人得到白己所报的钱数,而另一个人则得到剩余的钱;若两人所报的数字之和超过100且数目相同,则每个人得到50元。
【解】博弈三要素:
参与人集合: N = { 1 , 2 } N=\left\{1,2\right\} N={1,2}
战略集合: S t = { 0 , 1 , 2... , 100 } , t = 1 , 2 S_t=\left\{0,1,2...,100\right\},t=1,2 St={0,1,2...,100},t=1,2
参与人 i i i的支付:
u i = { s i 当 s i + s j ≤ 100 ( i , j = 1 或 2 ) s i 当 s i + s j > 100 , 且 s i < s j 100 − s j 当 s i + s j > 100 , 且 s i > s j 50 当 s i + s j > 100 , 且 s i = s j u_i= \begin{cases}s_i & \text { 当 } s_i+s_j \leq 100(i, j=1 \text { 或 } 2) \\ s_i & \text { 当 } s_i+s_j>100, \text { 且 } s_i<s_j \\ 100-s_j & \text { 当 } s_i+s_j>100, \text { 且 } s_i>s_j \\ 50 & \text { 当 } s_i+s_j>100, \text { 且 } s_i=s_j\end{cases} ui=⎩ ⎨ ⎧sisi100−sj50 当 si+sj≤100(i,j=1 或 2) 当 si+sj>100, 且 si<sj 当 si+sj>100, 且 si>sj 当 si+sj>100, 且 si=sj
相关文章:

【博弈论】【第一章】博弈论导论
博弈论导论 【例题】选择数字【例题】巴什博弈【例题】射手博弈博弈论的基本概念:参与人战略行动信息支付函数【例题】分100元 课程概述: 【例题】选择数字 两个参与人A和B,轮流选择[3,4,5,6,7,8,9]中的一个整数(可重复)。当累计…...

keil移植linux(makefile)
文章目录 运行环境:1.1 freeRTOS_LED工程移植1)修改cubeMX配置2)setting设置3)launch设置4)修改makefile5)修改代码6)实验效果 运行环境: ubuntu18.04.melodic 宏基暗影骑士笔记本 stm32f427IIH6 stlink 9-24v可调电源 robomaster A 板 1.1 freeRTOS_L…...

C++——类和对象(3)
作者:几冬雪来 时间:2023年5月6日 内容:C类和对象内容讲解 目录 前言: 1.运算符重载(续): 2.赋值重载: 结尾: 前言: 在上一篇博客中我们再一次讲解了…...

itop-3568开发板驱动学习笔记(24)设备树(三)时钟实例分析
《【北京迅为】itop-3568开发板驱动开发指南.pdf》 学习笔记 文章目录 生产者属性#clock-cells 属性clock-output-namesclock-frequencyassigned-clockclock-indicesassigned-clock-parents 消费者属性 设备树中的时钟信息以时钟树形式体现,时钟树包括时钟的属性和结…...
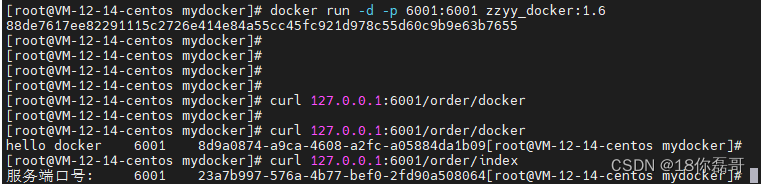
linux中使用docker部署微服务
目录 一、制作jar包(如果看一眼很简单,可以直接使用结尾的jar) 1.首先创建一个微服务 demo2 2.启动微服务(在DemoApplication上右键执行启动就行) 注意:其他操作导致的 可能遇到的报错 3.修改端口 4.新…...
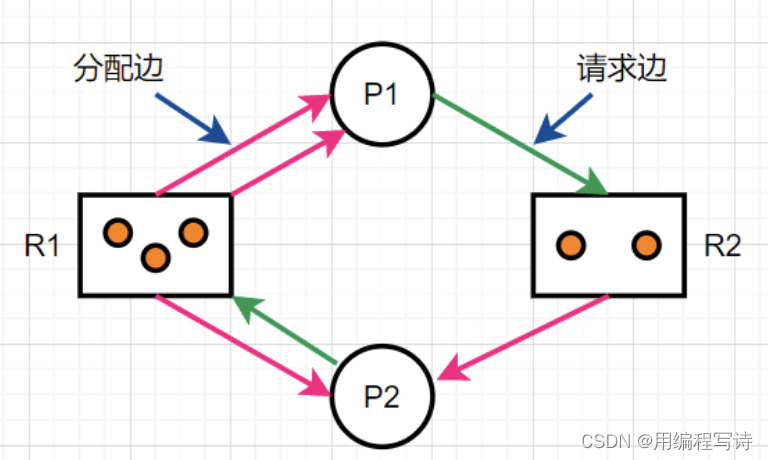
操作系统考试复习—第三章 优先级倒置 死锁问题
当前OS广泛采用优先级调度算法和抢占方式,然而在系统中存在着影响进程运行的资源从而可能产生"优先级倒置"现象 具体解释为:在原本的调度算法设计中,高优先级进程可以抢占低优先级的CPU资源,先执行高优先级任务。但是存…...

OpenHarmony送显流程分析
OpenHarmony送显流程分析 引言 本文档主要记录OpenHarmony在渲染完成之后如何进行合成和送显流程的。这个过程牵涉的代码很多,而且流程也是比较繁琐的。所以我一定要坚持下来。千万不能半途而废,也不要想着一口气吃出一个胖子,路漫漫其修远兮…...

Java面试题字节流字符流
String 编码UTF-8 和GBK的区别 GBK编码:是指中国的中文字符,其实它包含了简体中文与繁体中文字符,另外还有一种字符 “gb2312”,这种字符仅能存储简体中文字符。 UTF-8编码:它是一种全国家通过的一种编码&#x…...
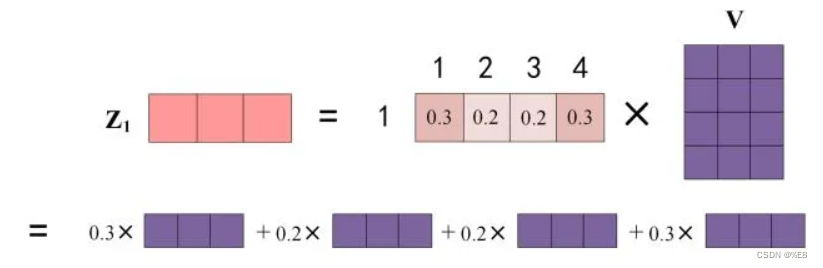
Self-Attention结构细节及计算过程
一、结构 上面那个图其实不是那么重要,只要知道将输入的x矩阵转换成三个矩阵进行计算即可。自注意力结构的输入为 输入矩阵的三个变形 Q(query矩阵)、K(key矩阵)、V(value矩阵)构成,…...
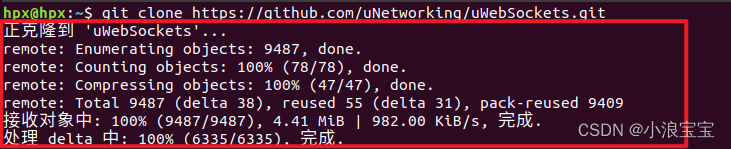
在Ubuntu18.04中安装uWebSockets库
目录 1.下载uWebSockets库2.下载uSockets3.安装openssl开发包4.编译首先说明这里使用的Ubuntu版本为18.04。 1.下载uWebSockets库 下载uWebSockets库有两种方式,一是终端,从Github中克隆uWebSockets库到Ubuntu本地文件夹,二是打开uWebSockets库下载链接自己下载到Windows,然…...

【Fluent】接着上一次计算的结果继续计算,利用计算过程中得到的物理场(温度、速度、压力等)插值Interpolate文件初始化模型的方法
一、问题背景 因为fluent中支持的初始化无非三种类型。 1、Standard initialization 标准初始化 2、Hybridinitialization 混合初始化 3、FMG initialization FMG初始化 另外,还可以用UDF通过坐标判断的方式予以初始化。 但是这些初始化方法都没办法利用以前计算过…...

第二十九章 使用消息订阅发布实现组件通信
PubSubJS库介绍 如果你想在React中使用第三方库来实现Pub/Sub机制,PubSubJS是一个不错的选择。它是一个轻量级的库,可以在浏览器和Node.js环境中使用。 PubSubJS提供了一个简单的API,可以让你在应用程序中订阅和发布消息。你可以使用npm来安…...
Transformer的位置编码
1. 什么是位置编码,为什么要使用位置编码 简单来说位置编码就是给一个句子中的每个token一个位置信息,通过位置编码可以明确token的前后顺序关系。 对任何语言来说,句子中词汇的顺序和位置都是非常重要的。它们定义了语法,从而定…...

Python学习简记
做题时遇到的不知道的知识点会更新在此: python中的int()函数可以用于进制转换 该函数最为常见的使用是用于强制类型转换,实际上,它可以有两个参数 值得强调的是当传入两个参数时第一个参数一定要是字符串类型 字符串方法: lower(…...
windows搭建一个FTP服务器超详细
一.场景: 在开发过程中需要FTP文件上传下载功能,需要在本地或者服务器上搭建一个FTP服务器。 二.详细步骤: 1. 安装FTP服务器支持和配置IIS web服务器 打卡“启动关闭Window功能” 控制面板>程序>启动或关闭Windows功能 或者选择快…...

u01使用率100%报错归档满的问题
今天下午客户报数据库无法连接了,我也立刻登录查看 因为显示orcl1归档满了,我就登录查看磁盘组的空间,发现空间空余很多 就sqlpus登录了,发现u01使用率满了 [oracledb1 ~]$ sqlplus / as sysdba SQL*Plus: Release 11.2.0.4.0 …...
Packet Tracer - 配置扩展 ACL - 场景 2
Packet Tracer - 配置扩展 ACL - 场景 2 拓扑图 地址分配表 设备 接口 IP 地址 子网掩码 默认网关 RTA G0/0 10.101.117.49 255.255.255.248 不适用 G0/1 10.101.117.33 255.255.255.240 不适用 G0/2 10.101.117.1 255.255.255.224 不适用 PCA NIC 10.101…...

最近面了12个人,发现这个测试基础题都答不上来...
一般面试我都会问一两道很基础的题目,来考察候选人的“地基”是否扎实,有些是操作系统层面的,有些是 python语言方面的,还有些… 深耕IT行业多年,我们发现,对于一个程序员而言,能去到一线互联网…...

JAVA基于Springboot框架的停车场管理系统开发实践和实现【附源码】
运行环境: jdk1.8idea/eclipsemaven3mysql5.6 项目技术: Java,Springboot,mybatis,mysql,jquery,html 该系统为停车场管理人员提供了对停车场中车辆,车位和财务的管理。操作员可以灵活地使用相关权限开展工作。在车位管理,车辆的停放和驶离、缴费&a…...

[230501] 4月29日考试真题第一篇|Temporary Pools
题目来源:http://t.csdn.cn/goCDT 正确率:6/10 目录 Temporary Pools 题目 Temporary Pools Paragraph 1: Temporary pools are freshwater habitats that retain water for only three to four months of the year or even shorter pe…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
