AtCoder Beginner Contest 300——A-G题讲解
蒟蒻来讲题,还望大家喜。若哪有问题,大家尽可提!
Hello, 大家好哇!本初中生蒟蒻讲解一下AtCoder Beginner Contest 300这场比赛的A-G题!
===========================================================================================
A - N-choice question
原题
Problem Statement
Given integers A A A and B B B, find A + B A+B A+B.
This is a N N N-choice problem; the i i i-th choice is C i C_i Ci.
Print the index of the correct choice.
Constraints
All values in the input are integers.
1 ≤ N ≤ 300 1 \le N \le 300 1≤N≤300
1 ≤ A , B ≤ 1000 1 \le A,B \le 1000 1≤A,B≤1000
1 ≤ C i ≤ 2000 1 \le C_i \le 2000 1≤Ci≤2000
C i C_i Ci are pairwise distinct. In other words, no two choices have the same value.
There is exactly one i i i such that A + B = C i A+B=C_i A+B=Ci. In other words, there is always a unique correct choice.
Input
The input is given from Standard Input in the following format:
N N N A A A B B B
C 1 C_1 C1 C 2 C_2 C2 … \dots … C N C_N CN
Output
Print the answer as an integer.
Sample Input 1
3 125 175
200 300 400
Sample Output 1
2
We have 125 + 175 = 300 125+175 = 300 125+175=300.
The first, second, and third choices are 200 200 200, 300 300 300, and 400 400 400, respectively.
Thus, the 2 2 2-nd choice is correct, so 2 2 2 should be printed.
Sample Input 2
1 1 1
2
Sample Output 2
1
The problem may be a one-choice problem.
Sample Input 3
5 123 456
135 246 357 468 579
Sample Output 3
5
题目大意
就是找出C序列中第几个数是A+B的和。
思路
太简单,不写了,直接见代码
代码
#include <iostream>using namespace std;int main()
{int n, a, b;cin >> n >> a >> b;int c = a + b, t;for (int i = 1; i<= n; i ++){cin >> t;if (t == c){cout << i << endl;return 0;}}
}
B - Same Map in the RPG World
原题
Problem Statement
Takahashi is developing an RPG. He has decided to write a code that checks whether two maps are equal.
We have grids A A A and B B B with H H H horizontal rows and W W W vertical columns. Each cell in the grid has a symbol # or . written on it.
The symbols written on the cell at the i i i-th row from the top and j j j-th column from the left in A A A and B B B are denoted by A i , j A_{i, j} Ai,j and B i , j B_{i, j} Bi,j, respectively.
The following two operations are called a vertical shift and horizontal shift.
For each j = 1 , 2 , … , W j=1, 2, \dots, W j=1,2,…,W, simultaneously do the following:
simultaneously replace A 1 , j , A 2 , j , … , A H − 1 , j , A H , j A_{1,j}, A_{2,j}, \dots, A_{H-1, j}, A_{H,j} A1,j,A2,j,…,AH−1,j,AH,j with A 2 , j , A 3 , j , … , A H , j , A 1 , j A_{2,j}, A_{3,j}, \dots, A_{H,j}, A_{1,j} A2,j,A3,j,…,AH,j,A1,j.
For each i = 1 , 2 , … , H i = 1, 2, \dots, H i=1,2,…,H, simultaneously do the following:
simultaneously replace A i , 1 , A i , 2 , … , A i , W − 1 , A i , W A_{i,1}, A_{i,2}, \dots, A_{i,W-1}, A_{i,W} Ai,1,Ai,2,…,Ai,W−1,Ai,W with A i , 2 , A i , 3 , … , A i , W , A i , 1 A_{i, 2}, A_{i, 3}, \dots, A_{i,W}, A_{i,1} Ai,2,Ai,3,…,Ai,W,Ai,1.
Is there a pair of non-negative integers ( s , t ) (s, t) (s,t) that satisfies the following condition? Print Yes if there is, and No otherwise.
After applying a vertical shift s s s times and a horizontal shift t t t times, A A A is equal to B B B.
Here, A A A is said to be equal to B B B if and only if A i , j = B i , j A_{i, j} = B_{i, j} Ai,j=Bi,j for all integer pairs ( i , j ) (i, j) (i,j) such that 1 ≤ i ≤ H 1 \leq i \leq H 1≤i≤H and 1 ≤ j ≤ W 1 \leq j \leq W 1≤j≤W.
Constraints
2 ≤ H , W ≤ 30 2 \leq H, W \leq 30 2≤H,W≤30
A i , j A_{i,j} Ai,j is # or ., and so is B i , j B_{i,j} Bi,j.
H H H and W W W are integers.
Input
The input is given from Standard Input in the following format:
H H H W W W
A 1 , 1 A 1 , 2 … A 1 , W A_{1,1}A_{1,2}\dots A_{1,W} A1,1A1,2…A1,W
A 2 , 1 A 2 , 2 … A 2 , W A_{2,1}A_{2,2}\dots A_{2,W} A2,1A2,2…A2,W
⋮ \vdots ⋮
A H , 1 A H , 2 … A H , W A_{H,1}A_{H,2}\dots A_{H,W} AH,1AH,2…AH,W
B 1 , 1 B 1 , 2 … B 1 , W B_{1,1}B_{1,2}\dots B_{1,W} B1,1B1,2…B1,W
B 2 , 1 B 2 , 2 … B 2 , W B_{2,1}B_{2,2}\dots B_{2,W} B2,1B2,2…B2,W
⋮ \vdots ⋮
B H , 1 B H , 2 … B H , W B_{H,1}B_{H,2}\dots B_{H,W} BH,1BH,2…BH,W
Output
Print Yes if there is a conforming integer pair ( s , t ) (s, t) (s,t); print No otherwise.
Sample Input 1
4 3
..#
...
.#.
...
#..
...
.#.
...
Sample Output 1
Yes
By choosing ( s , t ) = ( 2 , 1 ) (s, t) = (2, 1) (s,t)=(2,1), the resulting A A A is equal to B B B.
We describe the procedure when ( s , t ) = ( 2 , 1 ) (s, t) = (2, 1) (s,t)=(2,1) is chosen. Initially, A A A is as follows.
..#
...
.#.
...
We first apply a vertical shift to make A A A as follows.
...
.#.
...
..#
Then we apply another vertical shift to make A A A as follows.
.#.
...
..#
...
Finally, we apply a horizontal shift to make A A A as follows, which equals B B B.
#..
...
.#.
...
Sample Input 2
3 2
##
##
#.
..
#.
#.
Sample Output 2
No
No choice of ( s , t ) (s, t) (s,t) makes A A A equal B B B.
Sample Input 3
4 5
#####
.#...
.##..
..##.
...##
#...#
#####
...#.
Sample Output 3
Yes
Sample Input 4
10 30
..........##########..........
..........####....###.....##..
.....##....##......##...#####.
....####...##..#####...##...##
...##..##..##......##..##....#
#.##....##....##...##..##.....
..##....##.##..#####...##...##
..###..###..............##.##.
.#..####..#..............###..
#..........##.................
................#..........##.
######....................####
....###.....##............####
.....##...#####......##....##.
.#####...##...##....####...##.
.....##..##....#...##..##..##.
##...##..##.....#.##....##....
.#####...##...##..##....##.##.
..........##.##...###..###....
...........###...#..####..#...
Sample Output 4
Yes
题目大意
两个仅由# 和 . 组成的矩阵A和B,A的各行可以同时向右转动,最后边的列到最左边,各列可以同时向上转动,最上面的到最下面,问这种变动能否使得A和B相等。
思路
通过遍历和模拟就可以完成,比较简单,直接见代码。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 35;string a[N], b[N], mycp[N], mydp[N];
bool flag;
int nop;int main(){int h,w;cin >> h >> w;for(int i =1 ;i <= h; i ++) cin >> a[i];for(int i =1 ;i <= h; i ++) cin >> b[i];for(int i =1 ;i <= h; i ++) mycp[i] = a[i] + a[i];for(int i = 1; i <= h ;i ++){for(int j = 0; j <= w*2 -1 ;j ++){for(int x = 1; x <= h; x++){if(mycp[i].substr(j,w) == b[x]){nop = 1;for(int t = i; t <= h; t++) mydp[nop ++] = mycp[t].substr(j,w);for(int t = 1 ; t < i ; t++) mydp[nop ++] = mycp[t].substr(j,w);flag = 0;for(int t = 1; t <= nop ; t ++) if(mydp[t] != b[t]) flag = 1;if(flag == 0){cout <<"Yes"<<endl;return 0;} }}}}cout << "No" <<endl;return 0;
}
C - Cross
原题
Problem Statement
We have a grid with H H H horizontal rows and W W W vertical columns. We denote by ( i , j ) (i, j) (i,j) the cell at the i i i-th row from the top and j j j-th column from the left of the grid.
Each cell in the grid has a symbol # or . written on it. Let C [ i ] [ j ] C[i][j] C[i][j] be the character written on ( i , j ) (i, j) (i,j). For integers i i i and j j j such that at least one of 1 ≤ i ≤ H 1 \leq i \leq H 1≤i≤H and 1 ≤ j ≤ W 1 \leq j \leq W 1≤j≤W is violated, we define C [ i ] [ j ] C[i][j] C[i][j] to be ..
( 4 n + 1 ) (4n+1) (4n+1) squares, consisting of ( a , b ) (a, b) (a,b) and ( a + d , b + d ) , ( a + d , b − d ) , ( a − d , b + d ) , ( a − d , b − d ) (a+d,b+d),(a+d,b-d),(a-d,b+d),(a-d,b-d) (a+d,b+d),(a+d,b−d),(a−d,b+d),(a−d,b−d) ( 1 ≤ d ≤ n , 1 ≤ n ) (1 \leq d \leq n, 1 \leq n) (1≤d≤n,1≤n), are said to be a cross of size n n n centered at ( a , b ) (a,b) (a,b) if and only if all of the following conditions are satisfied:
C [ a ] [ b ] C[a][b] C[a][b] is #.
C [ a + d ] [ b + d ] , C [ a + d ] [ b − d ] , C [ a − d ] [ b + d ] C[a+d][b+d],C[a+d][b-d],C[a-d][b+d] C[a+d][b+d],C[a+d][b−d],C[a−d][b+d], and C [ a − d ] [ b − d ] C[a-d][b-d] C[a−d][b−d] are all #, for all integers d d d such that 1 ≤ d ≤ n 1 \leq d \leq n 1≤d≤n,
At least one of C [ a + n + 1 ] [ b + n + 1 ] , C [ a + n + 1 ] [ b − n − 1 ] , C [ a − n − 1 ] [ b + n + 1 ] C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1] C[a+n+1][b+n+1],C[a+n+1][b−n−1],C[a−n−1][b+n+1], and C [ a − n − 1 ] [ b − n − 1 ] C[a-n-1][b-n-1] C[a−n−1][b−n−1] is ..
For example, the grid in the following figure has a cross of size 1 1 1 centered at ( 2 , 2 ) (2, 2) (2,2) and another of size 2 2 2 centered at ( 3 , 7 ) (3, 7) (3,7).

The grid has some crosses. No # is written on the cells except for those comprising a cross.
Additionally, no two squares that comprise two different crosses share a corner. The two grids in the following figure are the examples of grids where two squares that comprise different crosses share a corner; such grids are not given as an input. For example, the left grid is invalid because ( 3 , 3 ) (3, 3) (3,3) and ( 4 , 4 ) (4, 4) (4,4) share a corner.

Let N = min ( H , W ) N = \min(H, W) N=min(H,W), and S n S_n Sn be the number of crosses of size n n n. Find S 1 , S 2 , … , S N S_1, S_2, \dots, S_N S1,S2,…,SN.
Constraints
3 ≤ H , W ≤ 100 3 \leq H, W \leq 100 3≤H,W≤100
C [ i ] [ j ] C[i][j] C[i][j] is # or ..
No two different squares that comprise two different crosses share a corner.
H H H and W W W are integers.
Input
The input is given from Standard Input in the following format:
$H$ $W$
$C[1][1]C[1][2]\dots C[1][W]$
$C[2][1]C[2][2]\dots C[2][W]$
$\vdots$
$C[H][1]C[H][2]\dots C[H][W]$
Output
Print S 1 , S 2 , … S_1, S_2, \dots S1,S2,…, and S N S_N SN, separated by spaces.
Sample Input 1
5 9
#.#.#...#
.#...#.#.
#.#...#..
.....#.#.
....#...#
Sample Output 1
1 1 0 0 0
As described in the Problem Statement, there are a cross of size 1 1 1 centered at ( 2 , 2 ) (2, 2) (2,2) and another of size 2 2 2 centered at ( 3 , 7 ) (3, 7) (3,7).
Sample Input 2
3 3
...
...
...
Sample Output 2
0 0 0
There may be no cross.
Sample Input 3
3 16
#.#.....#.#..#.#
.#.......#....#.
#.#.....#.#..#.#
Sample Output 3
3 0 0
Sample Input 4
15 20
#.#..#.............#
.#....#....#.#....#.
#.#....#....#....#..
........#..#.#..#...
#.....#..#.....#....
.#...#....#...#..#.#
..#.#......#.#....#.
...#........#....#.#
..#.#......#.#......
.#...#....#...#.....
#.....#..#.....#....
........#.......#...
#.#....#....#.#..#..
.#....#......#....#.
#.#..#......#.#....#
Sample Output 4
5 0 1 0 0 0 1 0 0 0 0 0 0 0 0
题目大意
从给点的矩阵中找由 #组成的图形,其中从中心 #往外一共有几层,按层数进行统计,分别输出1层、2层、3层……n层的个数。
思路
这道题我们可以枚举每一个#,对于每一个#,可以进行X型扩展,扩展的时候注意处理边界!(详情见代码吧!)
代码
#include <iostream>using namespace std;const int N = 1e2 + 10;int h, w;
char c[N][N];
int s[N];int main()
{cin >> h >> w;for (int i = 1; i <= h; i ++)for (int j = 1; j <= w; j ++)cin >> c[i][j];for (int i = 2; i < h; i ++)for (int j = 2; j < w; j ++)if (c[i][j] == '#'){int deep = 0;while (i + deep + 1 <= h && i - deep + 1 >= 1 && j - deep + 1 >= 1 && j + deep + 1 <= w && c[i + deep + 1][j - deep - 1] == '#' && c[i + deep + 1][j + deep + 1] == '#' && c[i - deep - 1][j - deep - 1] == '#' && c[i - deep - 1][j + deep + 1] == '#')deep ++;s[deep] ++;}for (int i = 1; i <= min(h, w); i ++)cout << s[i] << " ";return 0;
}
D - AABCC
原题
Problem Statement
How many positive integers no greater than N N N can be represented as a 2 × b × c 2 a^2 \times b \times c^2 a2×b×c2 with three primes a , b a,b a,b, and c c c such that a < b < c ?
Constraints
N N N is an integer satisfying 300 ≤ N ≤ 1 0 12 300 \le N \le 10^{12} 300≤N≤1012.
Input
The input is given from Standard Input in the following format:
N N N
Output
Print the answer as an integer.
Sample Input 1
1000
Sample Output 1
3
The conforming integers no greater than 1000 1000 1000 are the following three.
300 = 2 2 × 3 × 5 2 300 = 2^2 \times 3 \times 5^2 300=22×3×52
588 = 2 2 × 3 × 7 2 588 = 2^2 \times 3 \times 7^2 588=22×3×72
980 = 2 2 × 5 × 7 2 980 = 2^2 \times 5 \times 7^2 980=22×5×72
Sample Input 2
1000000000000
Sample Output 2
2817785
题目大意
对于质数 a , b a,b a,b, and c c c, a < b < c,问 a 2 × b × c 2 a^2 \times b \times c^2 a2×b×c2组成的小于N的数的个数。
思路
方法一:
由于 a 2 × b × c 2 ≤ N a^2 \times b \times c^2 \le N a2×b×c2≤N,且a < b < c,
所以 a 5 ≤ N a^5 \le N a5≤N, a ≤ 400 a \le 400 a≤400
对于b和c只需要遍历到 1 0 6 10^{6} 106就足够了。
所以先把 1 0 6 10^{6} 106的所有质数求出来,a只取前78个,其它的直接遍历计算就可以了。
方法二:
基本于方法一的思路 一样,只是对于C可以采用二分进行快速计算。
代码
方法一:
#include <iostream>
#include <cmath>
#include <vector>
#define int long long using namespace std;const int N = 1e6 + 10;int n;
vector<int> prime;
bool st[N];void div(int x)
{for (int i = 2; i <= x; i ++){if (!st[i]) prime.push_back(i);for (int j = 0; prime[j] <= x / i; j ++){st[i * prime[j]] = 1;if (i % prime[j] == 0) break;}}
}signed main()
{cin >> n;div(1000000);int res = 0;for (int i = 0; i < 78; i ++)for (int j = i + 1; prime[i] * prime[j] * prime[j] * prime[i] * prime[j] <= n; j ++)for (int k = j + 1; prime[i] * prime[j] * prime[k] * prime[i] * prime[k] <= n; k ++)res ++;cout << res << endl;return 0;
}
方法二:
#include <iostream>
#include <cmath>
#include <vector>
#define int long long using namespace std;const int N = 1e6 + 10;int n;
vector<int> prime;
bool st[N];void div(int x)
{for (int i = 2; i <= x; i ++){if (!st[i]) prime.push_back(i);for (int j = 0; prime[j] <= x / i; j ++){st[i * prime[j]] = 1;if (i % prime[j] == 0) break;}}
}signed main()
{cin >> n;div(290000);int res = 0;for (int i = 0; i < prime.size(); i ++)for (int j = i + 1; j < prime.size() && prime[j] * prime[i] <= 1e6; j ++){int l = j + 1, r = prime.size() - 1, t = 0;while (l <= r){int mid = l + r + 1 >> 1;if (prime[mid] * prime[i] <= 1e6 && (int)1ll * prime[i] * prime[j] * prime[mid] * prime[i] * prime[mid] <= n) l = mid + 1;else r = mid - 1;}res += l - j - 1;}cout << res << endl;return 0;
}
E - Dice Product 3
原题
Problem Statement
You have an integer 1 1 1 and a die that shows integers between 1 1 1 and 6 6 6 (inclusive) with equal probability.
You repeat the following operation while your integer is strictly less than N N N:
- Cast a die. If it shows x x x, multiply your integer by x x x.
Find the probability, modulo 998244353 998244353 998244353, that your integer ends up being N N N.
How to find a probability modulo 998244353 998244353 998244353?
We can prove that the sought probability is always rational.
Additionally, under the constraints of this problem, when that value is represented as P Q \frac{P}{Q} QP with two coprime integers P P P and Q Q Q, we can prove that there is a unique integer R R R such that R × Q ≡ P ( m o d 998244353 ) R \times Q \equiv P\pmod{998244353} R×Q≡P(mod998244353) and 0 ≤ R < 998244353 0 \leq R \lt 998244353 0≤R<998244353. Find this R R R.
Constraints
2 ≤ N ≤ 1 0 18 2 \leq N \leq 10^{18} 2≤N≤1018
N N N is an integer.
Input
The input is given from Standard Input in the following format:
$N$
Output
Print the probability, modulo 998244353 998244353 998244353, that your integer ends up being N N N.
Sample Input 1
6
Sample Output 1
239578645
One of the possible procedures is as follows.
Initially, your integer is 1 1 1.
You cast a die, and it shows 2 2 2. Your integer becomes 1 × 2 = 2 1 \times 2 = 2 1×2=2.
You cast a die, and it shows 4 4 4. Your integer becomes 2 × 4 = 8 2 \times 4 = 8 2×4=8.
Now your integer is not less than 6 6 6, so you terminate the procedure.
Your integer ends up being 8 8 8, which is not equal to N = 6 N = 6 N=6.
The probability that your integer ends up being 6 6 6 is 7 25 \frac{7}{25} 257. Since 239578645 × 25 ≡ 7 ( m o d 998244353 ) 239578645 \times 25 \equiv 7 \pmod{998244353} 239578645×25≡7(mod998244353), print 239578645 239578645 239578645.
Sample Input 2
7
Sample Output 2
0
No matter what the die shows, your integer never ends up being 7 7 7.
Sample Input 3
300
Sample Output 3
183676961
Sample Input 4
979552051200000000
Sample Output 4
812376310
题目大意
这道题的意思筛骰子,筛到每个数(即1-6)的概率均等,把所筛到的数相乘记作 T T T,筛到 T = N T=N T=N的概率是多少
思路
这道题可以想到DP,这里先给出一个简单的DP转移方程:
d p [ x ] = 1 5 ∑ i = 2 6 d p [ i × x ] dp[x]=\frac{1}{5}\displaystyle \sum_{i=2}^{6}dp[i \times x] dp[x]=51i=2∑6dp[i×x]
证明:
d p [ x ] = 1 6 d p [ 1 × x ] + 1 6 ∑ i = 2 6 d p [ i × x ] d p [ x ] − 1 6 d p [ 1 × x ] = 1 6 ∑ i = 2 6 d p [ i × x ] 5 6 d p [ x ] = 1 6 ∑ i = 2 6 d p [ i × x ] 5 6 d p [ x ] ÷ 5 6 = 1 6 ∑ i = 2 6 d p [ i × x ] ÷ 5 6 d p [ x ] = 1 5 ∑ i = 2 6 d p [ i × x ] \begin{equation*} \begin{split} & dp[x] = \frac{1}{6}dp[1\times x] + \frac{1}{6}\displaystyle \sum_{i=2}^{6}dp[i\times x]\\ & dp[x]-\frac{1}{6}dp[1\times x]=\frac{1}{6}\displaystyle \sum_{i=2}^{6}dp[i\times x]\\ & \frac{5}{6}dp[x]=\frac{1}{6}\displaystyle \sum_{i=2}^{6}dp[i\times x]\\ & \frac{5}{6}dp[x]\div \frac{5}{6}=\frac{1}{6}\displaystyle \sum_{i=2}^{6}dp[i\times x]\div \frac{5}{6}\\ & dp[x]=\frac{1}{5}\displaystyle \sum_{i=2}^{6}dp[i \times x] \end{split} \end{equation*} dp[x]=61dp[1×x]+61i=2∑6dp[i×x]dp[x]−61dp[1×x]=61i=2∑6dp[i×x]65dp[x]=61i=2∑6dp[i×x]65dp[x]÷65=61i=2∑6dp[i×x]÷65dp[x]=51i=2∑6dp[i×x]
但是,由于N很大,所以这样直接做肯定会TLE!
所以,我们想一想,因为有些数是不能被乘出来的,所以我们考虑哪些数会被乘出来!
因为乘的数只能是 2 , 3 , 4 , 5 , 6 2,3,4,5,6 2,3,4,5,6,所以其实就相当于只能是 2 , 3 , 5 2, 3, 5 2,3,5的幂。
即:分解质因数后有且仅有 2 , 3 , 5 2,3,5 2,3,5这三个数(数量没关系)
那么分别考虑:
若是2的幂:则只会有 log 2 1 0 18 \log_210^{18} log21018
若是3的幂:则只会有 log 3 1 0 18 \log_310^{18} log31018
若是5的幂:则只会有 log 5 1 0 18 \log_510^{18} log51018
所以最多只会有: log 2 1 0 18 × log 3 1 0 18 × log 5 1 0 18 \log_210^{18}\times \log_310^{18} \times \log_510^{18} log21018×log31018×log51018
时间复杂度肯定是可以接受的!
由于要考虑边界情况,所以我们可以用记忆化搜索来写,写的会简单点。对于题目中的 R × Q ≡ P ( m o d 998244353 ) R \times Q \equiv P\pmod{998244353} R×Q≡P(mod998244353) and 0 ≤ R < 998244353 0 \leq R \lt 998244353 0≤R<998244353,由于模数是质数,所以直接用快速幂求就行!
最后,输出的答案即为 d p [ 1 ] dp[1] dp[1],由于我们相当于倒着转移的。
代码
#include <iostream>
#include <unordered_map>
#define int long longusing namespace std;const int MOD = 998244353;int n, IE5;
unordered_map<int, int> val;inline int dp(int x)
{if (x > n) return 0;else if (x == n) return 1;else if (val.count((x))) return val[x];int res = 0;for (int i = 2; i <= 6; i ++) res += dp(i * x);res = res * IE5 % MOD;val[x] = res;return val[x];
}int qmi(int a, int b)
{int res = 1;while (b){if (b & 1) res = res * a % MOD;a = a * a % MOD;b >>= 1;}return res;
}void init()
{IE5 = qmi(5, MOD - 2);
}signed main()
{init();cin >> n;cout << dp(1) << endl;
}
F - More Holidays
原题
Problem Statement
You are given a string S S S of length N N N consisting of o and x, and integers M M M and K K K.
S S S is guaranteed to contain at least one x.
Let T T T be the string of length N M NM NM obtained by concatenating M M M copies of S S S.
Consider replacing exactly K K K x's in T T T with o.
Your objective is to have as long a contiguous substring consisting of o as possible in the resulting T T T.
Find the maximum length of a contiguous substring consisting of o that you can obtain.
Constraints
N N N, M M M, and K K K are integers.
1 ≤ N ≤ 3 × 1 0 5 1 \le N \le 3 \times 10^5 1≤N≤3×105
1 ≤ M ≤ 1 0 9 1 \le M \le 10^9 1≤M≤109
1 ≤ K ≤ x 1 \le K \le x 1≤K≤x, where x x x is the number of x's in the string T T T.
S S S is a string of length N N N consisting of o and x.
S S S has at least one x.
Input
The input is given from Standard Input in the following format:
N N N M M M K K K
S S S
Output
Print the answer as an integer.
Sample Input 1
10 1 2
ooxxooooox
Sample Output 1
9
S = S= S= ooxxooooox and T = T= T= ooxxooooox.
Replacing x at the third and fourth characters with o makes T = T= T= ooooooooox.
Now we have a length- 9 9 9 contiguous substring consisting of o, which is the longest possible.
Sample Input 2
5 3 4
oxxox
Sample Output 2
8
S = S= S= oxxox and T = T= T= oxxoxoxxoxoxxox.
Replacing x at the 5 , 7 , 8 5,7,8 5,7,8 and 10 10 10-th characters with o makes T = T= T= oxxooooooooxxox.
Now we have a length- 8 8 8 contiguous substring consisting of o, which is the longest possible.
Sample Input 3
30 1000000000 9982443530
oxoxooxoxoxooxoxooxxxoxxxooxox
Sample Output 3
19964887064
题目大意
字符串S由x和o组成,长度是N,M表示一共M个字符串S连接组成一个新的S,K表示在新的S中修改K个x为o,问S中最长o相连的子串的长度。
思路
因为S是M个重复字符串(每个长度为N)组成,所以如果第一个要改变的x一定在前N个字符中,此时可以有两种方法来做这个题。
方法一:
硬算,比赛时我就是硬算的,结果算的不对,导致时间不足了。
方法二:
采用遍历加二分的方法来完成。
1、对原始的S做一次前缀和,计算去前i个字符中x的个数。
2、对原始的S反过来再计算一次前缀和,计算第i个字符后x的个数。
3、计算原始的S共有多少个x,设为p
4、如果K > p,那么 NM长度的新S中K / p 个原S中的x都要转为o,K % p的x就要从前面的第一个S和后面的S中截取。所以只需要计算从第一个S中的第i位开始截取,到后面S的哪一位结束就可以了。这个过程,可以用二分来完成。
注意:求x个数的公式一定要仔细推,很容易推错!
写的简略了点,有问题可以问我!
代码
#include <iostream>
#define int long longusing namespace std;const int N = 3e5 + 10;int n, m, k, p;
int frw[N], rvs[N];
string s;bool check(int l, int r)
{int num_x = (r <= n) ? frw[r] - frw[l - 1] : rvs[l] + frw[r % n] + (r - n) / n * p;return num_x <= k;
}signed main()
{cin >> n >> m >> k >> s;s = ' ' + s;for (int i = 1; i <= n; i ++)frw[i] = frw[i - 1] + (s[i] == 'x'), p += (s[i] == 'x');for (int i = n; i >= 1; i --)rvs[i] = rvs[i + 1] + (s[i] == 'x');int res = 0;for (int i = 1; i <= n; i ++){int l = i, r = n * m;while (l < r){int mid = l + r + 1 >> 1;if (check(i, mid)) l = mid;else r = mid - 1;}res = max(res, l - i + 1);}cout << res << endl;
}G - P-smooth number
原题
Problem Statement
A positive integer is called a k k k-smooth number if none of its prime factors exceeds k k k.
Given an integer N N N and a prime P P P not exceeding 100 100 100, find the number of P P P-smooth numbers not exceeding N N N.
Constraints
N N N is an integer such that 1 ≤ N ≤ 1 0 16 1 \le N \le 10^{16} 1≤N≤1016.
P P P is a prime such that 2 ≤ P ≤ 100 2 \le P \le 100 2≤P≤100.
Input
The input is given from Standard Input in the following format:
N N N P P P
Output
Print the answer as an integer.
Sample Input 1
36 3
Sample Output 1
14
The 3 3 3-smooth numbers not exceeding 36 36 36 are the following 14 14 14 integers: 1 , 2 , 3 , 4 , 6 , 8 , 9 , 12 , 16 , 18 , 24 , 27 , 32 , 36 1,2,3,4,6,8,9,12,16,18,24,27,32,36 1,2,3,4,6,8,9,12,16,18,24,27,32,36.
Note that 1 1 1 is a k k k-smooth number for all primes k k k.
Sample Input 2
10000000000000000 97
Sample Output 2
2345134674
题目大意
计算N以内所有P的平滑数有多少个,其中P不超过100。
平滑数的定义:一个质因子不超过K的数,叫做K的平滑数。
思路
学习了一下官方的思路,这个题采用双向搜索(meet-in-the-middle trick),先从两端开始搜索,然后将结果放入两个集合中,最后将两个集合的混合计算。
注意:1是一个特殊的,永远是平滑数!
写的简略了点,有问题可以问我!
代码
#include <iostream>
#include <algorithm>
#include <vector>
#define int long longusing namespace std;int n, p;void push(vector<int> &a, int num)
{int sz = a.size();for (int i = 0; i < sz; i ++){int t = a[i];while (1){t *= num;if (t > n) break;a.push_back(t);}}
}signed main()
{vector<int> prime = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};cin >> n >> p;while (p < prime.back()) prime.pop_back();vector<int> frt = {1}, bck = {1};for (auto &c : prime)if (frt.size() < bck.size()) push(frt, c);else push(bck, c);sort(frt.begin(), frt.end());sort(bck.begin(), bck.end());int res = 0;for (int i = 0, j = bck.size() - 1; i < frt.size(); i ++){int left = n / frt[i];while (j >= 0 && left < bck[j]) j --;if (j < 0) break;res += j + 1;}cout << res << endl;
}本次题解的E题得到了国家队大佬刘一平老师的指点,感谢刘老师。
因为最近感冒,所以拖到现在才更新。
今天就到这里了!
大家有什么问题尽管提,我都会尽力回答的!
吾欲您伸手,点的小赞赞。吾欲您喜欢,点得小关注!
相关文章:

AtCoder Beginner Contest 300——A-G题讲解
蒟蒻来讲题,还望大家喜。若哪有问题,大家尽可提! Hello, 大家好哇!本初中生蒟蒻讲解一下AtCoder Beginner Contest 300这场比赛的A-G题! A - N-choice question 原题 Problem Statement Given integers A A A and…...

Go:值与指针
1. 计算机中的值 在百万年的演化历史中,人类对事物的属性进行了抽象,有了数量、精度、信息等概念的表示,对应的我们称之为整数、小数、文本文字等。计算机出现后,我们使用计算机对真实世界的问题进行建模,通过计算机的…...

【Linux】进程学习(2)---理解进程操作
文章目录 查看进程通过系统目录查看通过ps命令查看 通过系统调用获取进程标识符通过系统调用创建进程初识fork函数fork函数的返回值 进程状态阻塞与运行状态Linux内核源码中的进程状态运行状态-R浅度睡眠状态-S深度睡眠状态-D暂停状态-T僵尸状态-Z死亡状态-X 查看进程 通过系统…...

基于springcloud实现的医院信息系统
访问【WRITE-BUG数字空间】_[内附完整源码和文档] 医疗信息就诊系统,系统主要功能按照数据流量、流向及处理过程分为临床诊疗、药品管理、财务管理、患者管理。诊疗活动由各工作站配合完成,并将临床信息进行整理、处理、汇总、统计、分析等。本系统包括以…...
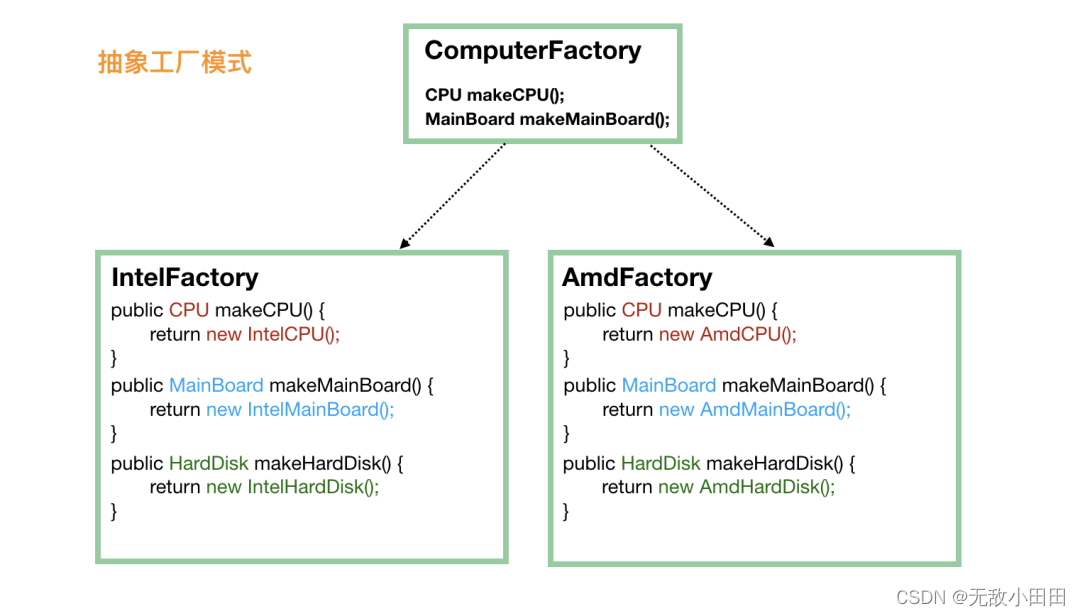
设计模式-创建型模式-(工厂、简单工厂、抽象工厂)
一、简单工厂模式 上代码 public class FoodFactory {public static Food makeFood(String name) {if (name.equals("noodle")) {Food noodle new LanZhouNoodle();noodle.addSpicy("more");return noodle;} else if (name.equals("chicken")…...

JAVA12新特性
JAVA12新特性 概述 2019年3月19日,java12正式发布了,总共有8个新的JEP(JDK Enhancement Proposals) JDK 12 is the open-source reference implementation of version 12 of the Java SE12 Platform as specified by by JSR 386 in the Java Community Process. JDK 12 reac…...

Nginx 静态文件、反向代理、负载均衡、缓存、SSL/TLS 加密、gzip 压缩 等等
Nginx的功能 1. 静态文件服务器2. 反向代理服务器3. 负载均衡4. 缓存5. SSL/TLS 加密6. URL 重写7. HTTP/28. WebSocket9. 反向代理缓存10. 安全限制11. gzip 压缩12. 请求限速13. 日志记录14. SSL 证书续订 Nginx 是一个高性能的开源 Web 服务器和反向代理服务器,它…...

Linux设备驱动模型(一)
一、sysfs文件系统 sysfs是一个虚拟文件系统,将内核总的设备对象的链接关系,以文件目录的方式表示出来,并提对设备提供读写接口。 二、kobject kobject是内核中对象表示的基类,可以认为所有的内核对象都是一个kobject kobject单…...

【Python入门篇】——Python基础语法(标识符与运算符)
作者简介: 辭七七,目前大一,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: Python入门,本专栏主要内容为Python的基础语法,Python中的选择循环语句…...

扩展 VirtualBox 已分配磁盘的方法
扩展 VirtualBox 已分配磁盘的方法 第一步:用VirtualBox命令行调整已分配磁盘的大小第二步:用windows磁盘管理工具扩展磁盘空间其他无关配置如何选择虚拟机的芯片组 注意:扩展操作只支持 vdi 格式的磁盘,就是VirtualBox自己的磁盘…...

【LeetCode】646. 最长数对链
646. 最长数对链(中等) 思路 这道题和 300. 最长递增子序列 类似,我们可以定义 dp 数组,其中 dp[i] 表示以 i 结尾的子序列的性质。在处理好每个位置后,统计一遍各个位置的结果即可得到题目要求的结果。 但是题目中强…...

Makefile教程(Makefile的结构)
文章目录 前言一、Makefile的结构二、深入案例三、Makefile中的一些技巧总结 前言 一、Makefile的结构 Makefile 通常由一系列规则组成,每条规则定义了如何从源文件生成目标文件。每个规则又由目标、依赖和命令三部分组成。 下面是 Makefile 规则的基本结构&…...

SpringMVC(后)SSM整合
10、文件上传和下载 10.1、文件下载 ResponseEntity用于控制器方法的返回值类型,该控制器方法的返回值就是响应到浏览器的响应报文 使用ResponseEntity实现下载文件的功能 RequestMapping("/testDown") public ResponseEntity<byte[]> testResp…...
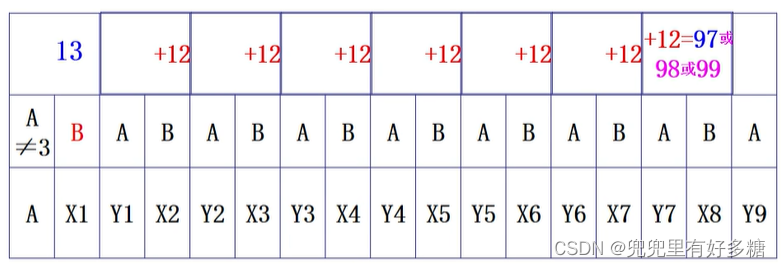
【博弈论】【第一章】博弈论导论
博弈论导论 【例题】选择数字【例题】巴什博弈【例题】射手博弈博弈论的基本概念:参与人战略行动信息支付函数【例题】分100元 课程概述: 【例题】选择数字 两个参与人A和B,轮流选择[3,4,5,6,7,8,9]中的一个整数(可重复)。当累计…...

keil移植linux(makefile)
文章目录 运行环境:1.1 freeRTOS_LED工程移植1)修改cubeMX配置2)setting设置3)launch设置4)修改makefile5)修改代码6)实验效果 运行环境: ubuntu18.04.melodic 宏基暗影骑士笔记本 stm32f427IIH6 stlink 9-24v可调电源 robomaster A 板 1.1 freeRTOS_L…...

C++——类和对象(3)
作者:几冬雪来 时间:2023年5月6日 内容:C类和对象内容讲解 目录 前言: 1.运算符重载(续): 2.赋值重载: 结尾: 前言: 在上一篇博客中我们再一次讲解了…...

itop-3568开发板驱动学习笔记(24)设备树(三)时钟实例分析
《【北京迅为】itop-3568开发板驱动开发指南.pdf》 学习笔记 文章目录 生产者属性#clock-cells 属性clock-output-namesclock-frequencyassigned-clockclock-indicesassigned-clock-parents 消费者属性 设备树中的时钟信息以时钟树形式体现,时钟树包括时钟的属性和结…...
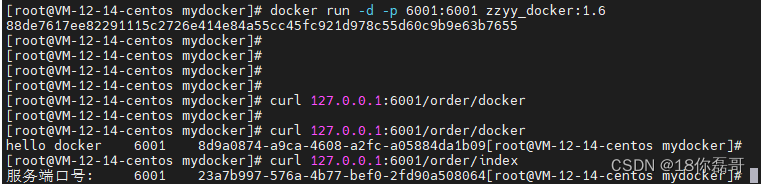
linux中使用docker部署微服务
目录 一、制作jar包(如果看一眼很简单,可以直接使用结尾的jar) 1.首先创建一个微服务 demo2 2.启动微服务(在DemoApplication上右键执行启动就行) 注意:其他操作导致的 可能遇到的报错 3.修改端口 4.新…...
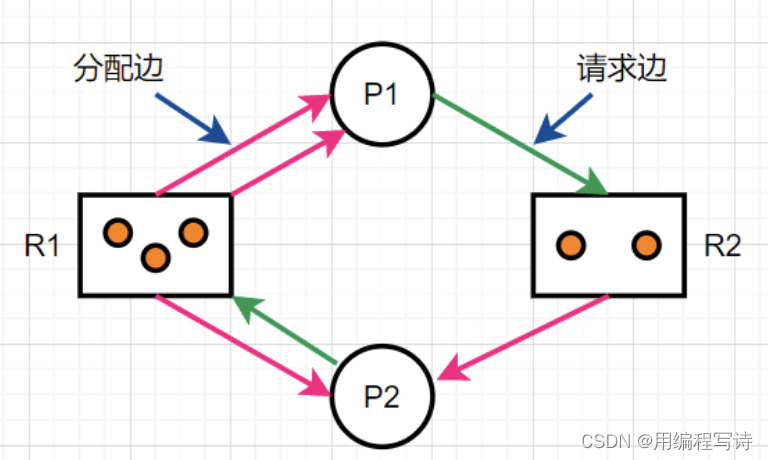
操作系统考试复习—第三章 优先级倒置 死锁问题
当前OS广泛采用优先级调度算法和抢占方式,然而在系统中存在着影响进程运行的资源从而可能产生"优先级倒置"现象 具体解释为:在原本的调度算法设计中,高优先级进程可以抢占低优先级的CPU资源,先执行高优先级任务。但是存…...

OpenHarmony送显流程分析
OpenHarmony送显流程分析 引言 本文档主要记录OpenHarmony在渲染完成之后如何进行合成和送显流程的。这个过程牵涉的代码很多,而且流程也是比较繁琐的。所以我一定要坚持下来。千万不能半途而废,也不要想着一口气吃出一个胖子,路漫漫其修远兮…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
