( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数
难度:中等
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O ( 1 ) O(1) O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
提示:
- 1 < = n < = 1 0 5 1 <= n <= 10^5 1<=n<=105
- nums.length == n + 1
- 1 <= nums[i] <= n
- nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
- 如何证明
nums中至少存在一个重复的数字? - 你可以设计一个线性级时间复杂度 O ( n ) O(n) O(n) 的解决方案吗?
💡思路:
法一:二分查找
由于数组中存储的数的范围是[1,n]且是连续的,所以我们可以进行二分查找,遍历数组统计小于等于数组中整数范围的中点mid的个数cnt:
- 如果
cnt > mid则重复的数一定在mid左边; - 否则一定在
mid的右边。 - 然后区间对半缩小,直到
l > h时,l即为重复的数。
法二:快慢指针
- 类似于有环链表中找出环的入口:
我们对 nums 数组建图,每个位置 i 连一条 i → nums[i]的边。由于存在的重复的数字 target,因此 target这个位置一定有起码两条指向它的边,因此整张图一定存在环,且我们要找到的 target 就是这个环的入口
对示例1进行建图,如下:
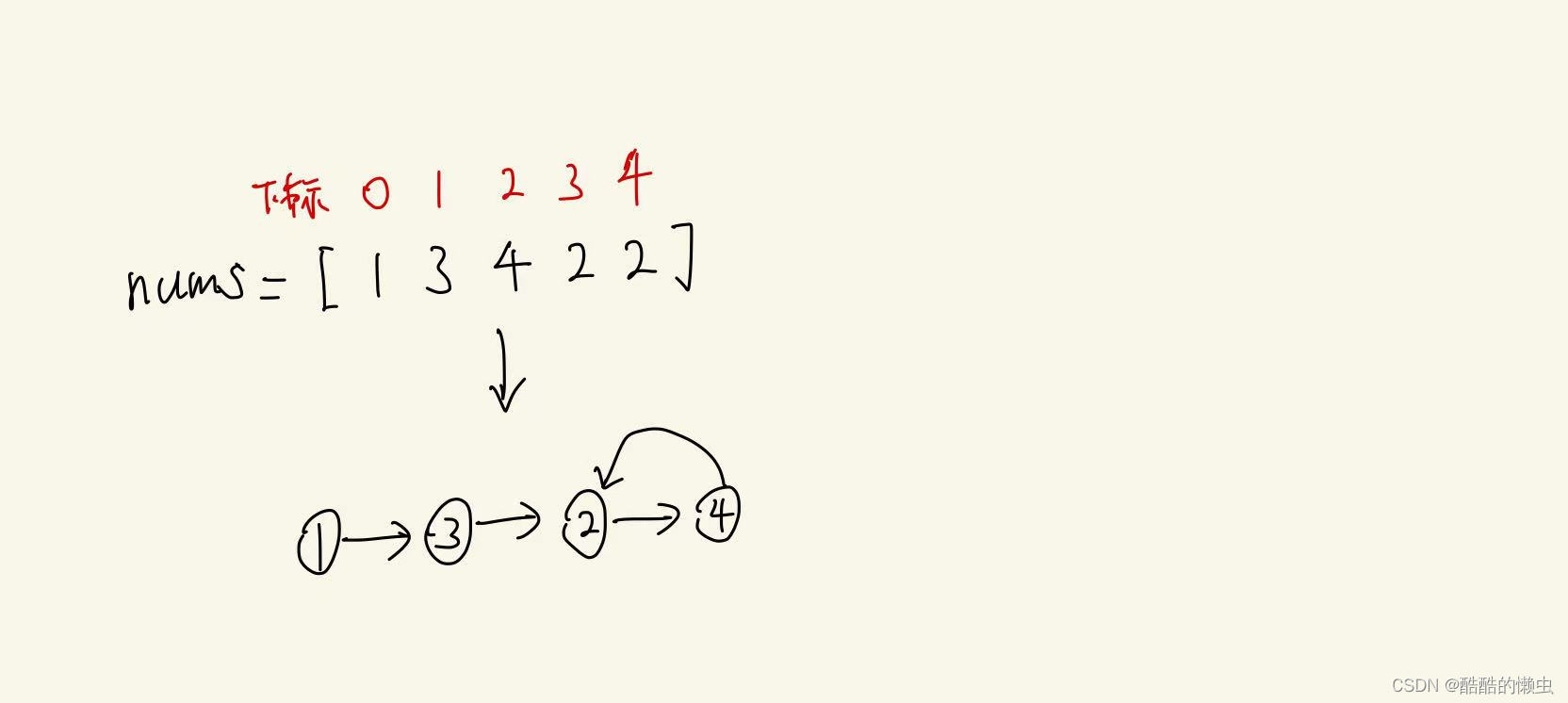
有两条边指向2,2即是环的入口,也是我们要找的target:
- 我们先设置慢指针
slow和快指针fast,慢指针每次走一步,快指针每次走两步,根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇; - 此时我们再将
slow放置起点0,两个指针每次同时移动一步,相遇的点就是答案。
这里简单证明为什么后面将
slow放置起点后移动相遇的点就一定是答案了。
假设环长为L,从起点到环的入口的步数是a,从环的入口继续走b步到达相遇位置,从相遇位置继续走c步回到环的入口,则有b+c= L,其中L、a、b、c都是正整数。
根据上述定义,慢指针走了
a+b步,快指针走了2(a+b)步。从另一个角度考虑,在相遇位置,快指针比慢指针多走了若干圈,因此快指针走的步数还可以表示成a+b+kL,其中k表示快指针在环上走的圈数。联立等式,可以得到:
2 ( a + b ) = a + b + k L 2(a+b)=a+b+kL 2(a+b)=a+b+kL
解得a = kL − b,整理可得:
a = ( k − 1 ) L + ( L − b ) = ( k − 1 ) L + c a=(k−1)L+(L−b)=(k−1)L+c a=(k−1)L+(L−b)=(k−1)L+c
从上述等式可知,如果慢指针从起点出发,快指针从相遇位置出发,每次两个指针都移动一步,则慢指针走了a步之后到达环的入口,快指针在环里走了k−1圈之后又走了c步,由于从相遇位置继续走c步即可回到环的入口,因此快指针也到达环的入口。两个指针在环的入口相遇,相遇点就是答案。
🍁代码:(Java、C++)
法一:二分查找
Java
class Solution {public int findDuplicate(int[] nums) {int l = 1, h = nums.length - 1;while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int num : nums){if(num <= mid){cnt++;}}if(cnt > mid) h = mid - 1;else l = mid + 1;}return l;}
}
C++
class Solution {
public:int findDuplicate(vector<int>& nums) {int l = 1, h = nums.size() - 1;while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int num : nums){if(num <= mid){cnt++;}}if(cnt > mid) h = mid - 1;else l = mid + 1;}return l;}
};
法二:快慢指针
Java
class Solution {public int findDuplicate(int[] nums) {int slow = nums[0], fast = nums[nums[0]];while(slow != fast){slow = nums[slow];fast = nums[nums[fast]];}slow = 0;while(slow != fast){slow = nums[slow];fast = nums[fast];}return slow;}
}
C++
class Solution {
public:int findDuplicate(vector<int>& nums) {int slow = nums[0], fast = nums[nums[0]];while(slow != fast){slow = nums[slow];fast = nums[nums[fast]];}slow = 0;while(slow != fast){slow = nums[slow];fast = nums[fast];}return slow;}
};
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中
n为 n u m s nums nums 数组的长度,「Floyd 判圈算法」时间复杂度为线性的时间复杂度;二分查找时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn), 二分查找最多需要二分 O ( l o g n ) O(logn) O(logn)。 - 空间复杂度: O ( 1 ) O(1) O(1),我们只需要常数空间存放若干变量。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度:中等 给定一个包含 n 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。 你…...

【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...

武忠祥老师每日一题||定积分基础训练(三)
常用的基本不等式: sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...

Docker安装常用软件-Apollo(有问题)
零:apollo概念介绍 官网网站:GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址:mirrors / ctripcorp / apollo GitCode …...

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...
)
如何使用二元三次回归分析建立预测模型?(分析、原理、代码示例)
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型,常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型,其中包括两个自变量(通常…...
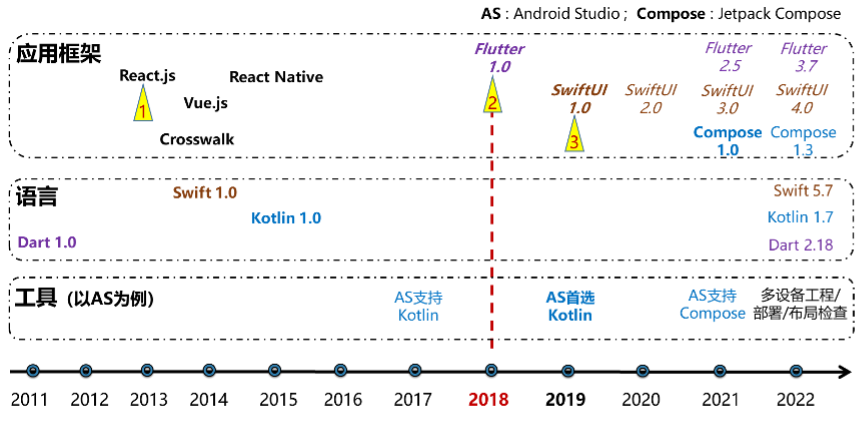
面向万物智联的应用框架的思考和探索(上)
原文:面向万物智联的应用框架的思考和探索(上),点击链接查看更多技术内容。 应用框架,是操作系统连接开发者生态,实现用户体验的关键基础设施。其中,开发效率和运行体验是永恒的诉求,…...

《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习,是一个交叉学科,是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期,使用专家设计的规则体系来设计。 缺点&…...

ClickHouse 内存管理是如何实现的
概述 本文介绍Clickhouse内存管理的实现原理。通过本文的分析,可以对Clickhouse的内存管理有一个概要的理解。 Clickouse内存管理组成 ClickHouse 使用内存管理系统来控制内存资源的分配和释放。内存管理系统的主要组成部分是: 内存池:Cl…...

docker容器技术
什么是docker Docker 使用 Google 公司推出的 Go 语言 进行开发实现,基于 Linux 内核的 cgroup,namespace,以及 OverlayFS 类的 Union FS 等技术,对进程进行封装隔离,属于 操作系统层面的虚拟化技术。由于隔离的进程独…...
设计模式七大设计原则
文章目录 1、什么是设计模式2、单一职责原则3、开闭原则4、接口隔离原则5、依赖倒置原则6、迪米特法则(最少知道原则)7、里式替换原则8、组合优于继承 设计模式主要是为了满足一个字 变,这个字,可能是需求变更、可能是场景变更&a…...
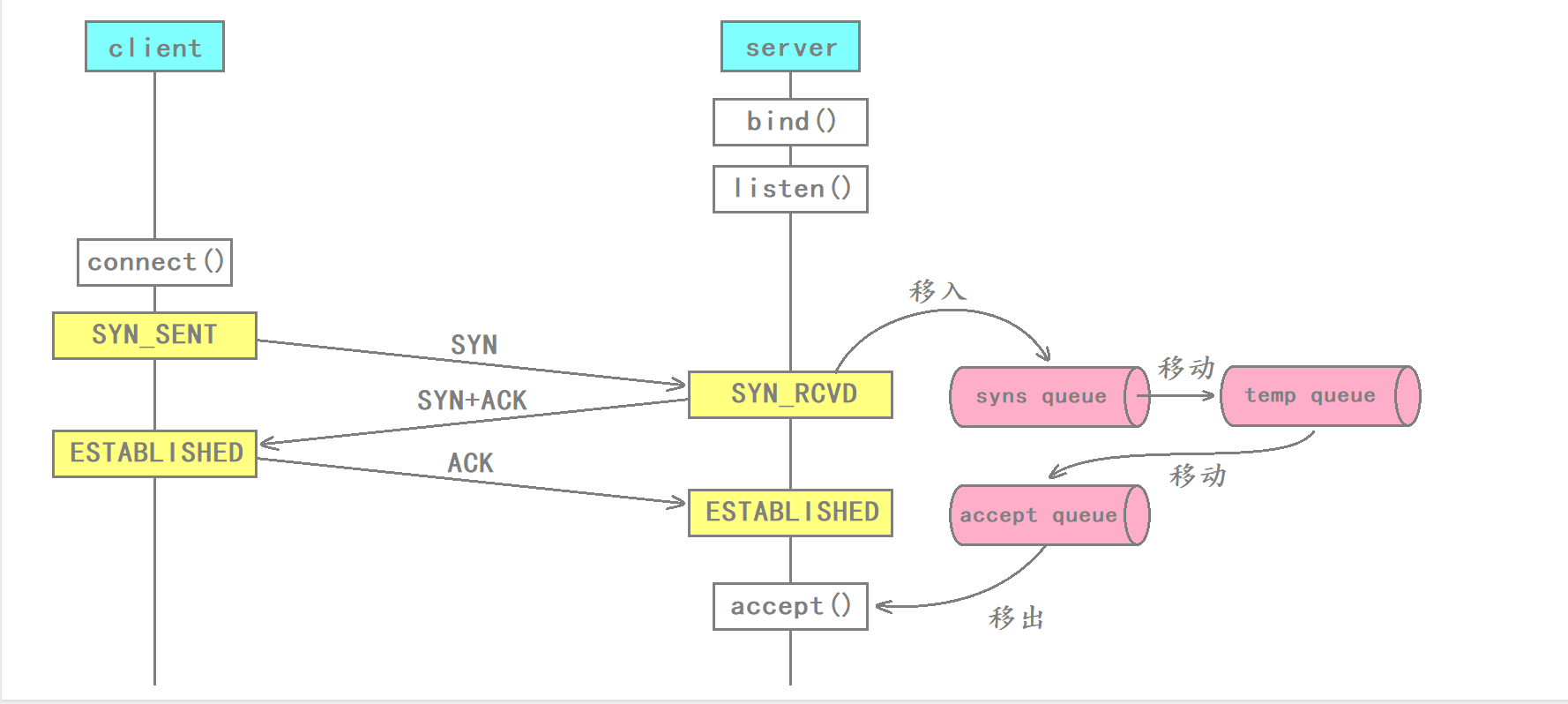
【Hello Network】TCP协议相关理解
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:补充下对于TCP协议的各种理解 TCP协议相关实验 TCP相关试验理解CLOSE_WAIT状态理解TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法理解listen的…...

实施CRM目标有哪几步?如何制定CRM目标?
在当今竞争激烈的商业环境中,与客户建立持久的关系是企业重要的工作。CRM客户管理系统能有效帮助企业管理优化流程、管理客户,提高销售成功率,推动收入增长。那么您了解如何实施CRM吗?下面说说实施CRM目标是什么,如何设…...
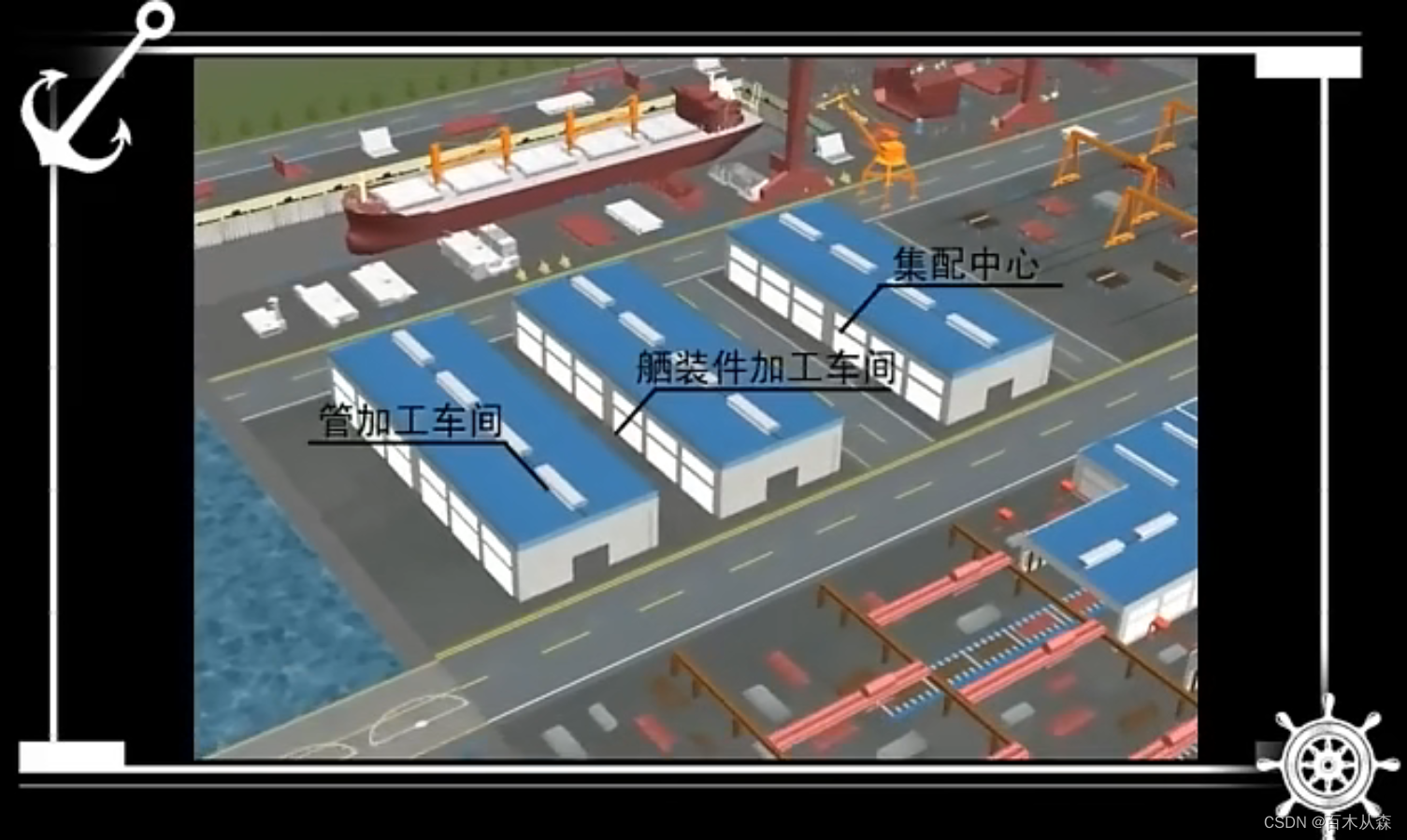
船舶建造概论(船舶建造工艺任务与现代造船模式)
船舶建造概论 1 船舶建造概论1.1 船舶建造工艺主要任务1.2 船舶建造流程(1)钢材料预处理(2) 钢材料加工(3)分段制作(4)总段制作(5)船台合拢(6&…...

项目内训(2023.5.6)
目录 Nacos是什么? 领域模型是什么? domain模块一般是干什么的? 在小乌龟中合并其他分支的作用是什么? nacos的配置文件 服务集群、服务提供、服务更加灵活庞大、消费服务、访问比较麻烦,A和B服务一起访问 系统结…...

【操作系统OS】学习笔记第二章 进程与线程(下)【哈工大李治军老师】
基于本人观看学习 哈工大李治军老师主讲的操作系统课程 所做的笔记,仅进行交流分享。 特此鸣谢李治军老师,操作系统的神作! 如果本篇笔记帮助到了你,还请点赞 关注 支持一下 ♡>𖥦<)!! 主页专栏有更多࿰…...
)
Linux命令集(Linux文件管理命令--rmdir指令篇)
Linux命令集(Linux文件管理命令--rmdir指令篇) Linux文件管理命令集(rmdir指令篇)5. rmdir(remove directory)1. 删除空的目录 folder12. 强制删除目录 folder1(包括非空目录)3. 递归删除目录及其目录下所有…...

在技术圈超卷的当下,学历到底是敲门砖还是枷锁?
前言 最近,突然之间被“孔乙己文学”刷屏了,短时间内“孔乙己文学”迅速走红,孔乙己是中国文学中的一位经典人物,他的长衫被认为是他的象征之一,孔乙己的长衫折射出很多现象,既有社会的,也有教育…...

Linux cgroup
前言 Cgroup和namespace类似,也是将进程进程分组,但是目的与namespace不一样,namespace是为了隔离进程组之前的资源,而Cgroup是为了对一组进程进行统一的资源监控和限制。 Cgroup的组成 subsystem 一个subsystem就是一个内核模…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
