B-Tree (多路查找树)分析-20230503
B-Tree (多路查找树)学习-20230503
- 前言
B-树是一类多路查询树,它主要用于文件系统和某些数据库的索引,如果采用二叉平衡树访问文件里面的数据,最坏情况下,磁头可能需要进行O(h)次对磁盘的读写,其中h为树的高度;此时如果采用B-树,由于它的多路访问特性可显著降低树的高度,所以对磁盘读写次数将大幅减少。
为了更清楚表述,我们引入经典的二次储存系统,为了增加储存容量,通常由多个磁盘构成,如果可以多路对磁盘进行访问,那么通过一次读取,很快可以定位数据的储存区域。

- B-Tree 的定义
根据《数据结构》(严蔚敏)定义一颗m阶的B-tree,或为空树,或满足下列特性的m叉树,
- 树中每个结点至多有m棵树,它定义节点中包含数据的上限值,此值和每个track的容量相关,由于B-tree的节点即储存键值,又储存子树指针,一般情况下键值会占据大量的数据空间,尤其是键值为结构体数据类型的时候,空间占据会急剧增加,为了应对这类挑战,人们发明了B+tree的数据结构
- 若根节点不是叶子节点,则至少有两棵树。此约束保证了B-tree不会退化为线性表,最坏情况下,允许退化为二叉树,这是最后的底线
- 除根节点之外的非终端节点至少有[m/2]棵子树,其中[m/2]取上限值
- 为了后续的程序操作方便,定义非终端结点包含下列数据信息的数据
( n , A 0 , K 1 , A 1 , K 2 , A 2 , . . . , K n , A n ) ; (n,A_0,K_1,A_1,K_2,A_2,...,K_n,A_n); (n,A0,K1,A1,K2,A2,...,Kn,An);
其中Ki为关键字,且K[i]<K[i+1],并且A[i-1]所指向的节点里面的关键字均小于K[i]关键字,A[i+1]所指向节点里面的关键字均大于K[i],n为关键字的数量([m/2]-1<=n<=m)
- 所有的叶子节点都在同一层次上,并且不带信息
- B-Tree 基本操作
3.1 查询操作
B-Tree树的查询操作与二叉查询树的查询操作类似。它实际上上分为两部分,第一部分需要找到值所在的节点的指针,然后在节点中可以采用顺序表搜索或者折半查找的方式定位待查询的值或者值所在的子树(指针),它是查找节点和在节点中搜索关键字的交叉进行的过程。

具体看一个例子,假定要查找key=99的值,从根节点出发,由于99>35,那么顺着A1指针指向的结点进行搜索,在A1指向的结点中,由于99>78,继续在A2所指的结点中搜索,在A2结点当中恰好K1=99,搜索完毕。
3.2 插入操作
B-Tree的生成是不断通过插入操作实现的,增加B-Tree高度唯一的途径是根节点的分裂,每次根节点分类事件发生,B-Tree的深度就增加1。除此之外,其它的插入也可能差生节点的分裂,但只要根节点不产生分裂,那么B-tree的深度就保持不变。
由于节点内关键字数目的限制,插入操作可能会导致节点分裂,这也导致了插入过程的复杂化。具体而言,插入某个值可以采用两个策略当中的任意一个,策略1 首先在最底层的某个非终端节点条件一个关键字,若该节点的数目不超过m-1,则插入完成,否则要产生节点的分裂,策略1实际上采用的是自下而上的方法,先从根节点出发,找到需要插入节点在最底层非终端节点上位置,然后执行插入,如果必要,则自下而上进行不断分裂。
具体看一个例子。对于m=3阶B-Tree,[m/2]=2。

假定需要依次插入关键字30,26,85和7,首先查找确定关键字应该插入的最底层结点的位置。通过查找得知,30应该插入在结点d所在位置,插入完成后,由于插入后的关键字数量小于m,无需任何分裂,插入作业完成。

同样查找关键字26亦应插入在d结点当中,由于d结点中关键在数目超过2,此时需要将d分裂成为两个结点,关键字26及其前后指针仍然保留在d结点中,而关键字37及其前后指针需要储存到新产生的结点d’当中。同时将中间关键字30和d’指针,一起插入到双亲结点中。由于更新后的b结点关键字未超过2,则插入完成。

结点d分裂为d和d’两个不同的结点。

类似地,在g中插入85后,需要分裂为两个结点,而当70插入到e结点当中去,由于e中的结点数目超过2,需要继续分裂;直到70插入到a结点中,插入结束。

85关键字插入后,g节点关键字数目不满足b-tree节点数目的基本要求,需要进行分裂,中间关键字70需要往移动到上一层节点e中去。由于70关键字的插入,导致 e结点关键字数量超过2,对于e结点需要继续分裂,中间关键字70继续往上移动至 结点a当中。

e结点分裂后的B-tree.

采用相同的思路,插入关键字7,通过查找关键字7应当插入至底层结点c当中,插入c后,由于c结点中的关键字数量大于2,需要分裂,关键字7移动至结点b当中,类似地,b结点中的关键字数量大于2;中间关键字24继续向上插入至根节点,由于根节点关键字数量大于2,根节点需要分裂,B-tree深度增加1,至此插入结束。
3.3 删除操作
B-Tree的删除操作比较复杂,其主要约束来自于B-tree特性的保持,一般情况下,则首先找到待删除关键字所在的结点,如果关键字所在结点为最下层的非终端节点,如果关键字数目不小于[m/2],直接删除即可,否则就需要自下而上进行结点的合并。倘若删除关键字为非终端结点Ki,则可以用指针Ai所指的树的最小关键字Y代替Ki,然后在相应的结点中删除Y即可。所以只需讨论删除最下层非终端结点的关键字即可。
有下列三种情况:
(1) 被删除关键字结点中的关键字数量不小于[m/2],则直接删除Ki和Ai即可,树的其它部分保持不变化。从树中删除关键字12就属于此类型。

删除12后,树的其它部分保持不变。

(2)被删除关键字所在的结点关键字数目为[m/2]-1,而与该节点相邻的右(左)兄弟结点的关键字数目大于[m/2]-1,则需将相邻右兄弟结点中最小(最大)的关键字上移至双亲结点中,而将双亲结点中小于(大于)且紧靠该上移关键字的关键字下移至被删除的结点当中。删除B-tree的关键字50便是如此情形。

(3)被删除关键字所在结点的左右子树关键字的数目都等于[m/2]-1, 假设该节点有右兄弟,且右兄弟结点由双亲结点中的Ai指针所指,那么在删除关键字之后,它所在的结点剩余的关键字和指针,另外加上双亲结点的Ki关键字合并到Ai所指的有兄弟结点中去。合并至左节点的逻辑亦相同。
删除关键字53,便是上述情形。

- 小结
由于B-tree的定义限制,导致 B-tree在插入和操作的时候需要分裂或合并结点,造成整体程序实现的复杂性。其实现方式通常采用自下而上,根据约束条件不断进行分裂或合并,直至根节点。另外B-tree深度增加的唯一途径就是根节点的分裂,B-tree深度减低的唯一途径就是根节点的合并。
参考文献:
并结点,造成整体程序实现的复杂性。其实现方式通常采用自下而上,根据约束条件不断进行分裂或合并,直至根节点。另外B-tree深度增加的唯一途径就是根节点的分裂,B-tree深度减低的唯一途径就是根节点的合并。
对于代码实现,如果有时间,我们将另外篇幅描述。
参考文献:
- 《数据结构》 严蔚敏
相关文章:

B-Tree (多路查找树)分析-20230503
B-Tree (多路查找树)学习-20230503 前言 B-树是一类多路查询树,它主要用于文件系统和某些数据库的索引,如果采用二叉平衡树访问文件里面的数据,最坏情况下,磁头可能需要进行O(h)次对磁盘的读写,其中h为树的高度&…...
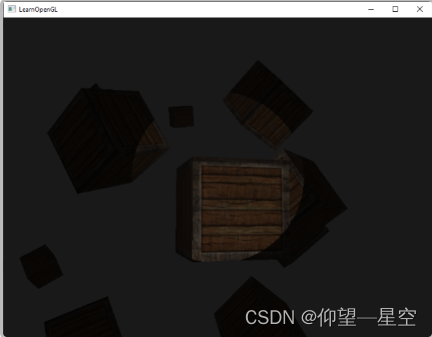
OpenGL光照教程之 透光物
引言 我们目前使用的所有光照都来自于一个单独的光源,这是空间中的一个点。它的效果不错,但是在真实世界,我们有多种类型的光,它们每个表现都不同。一个光源把光投射到物体上,叫做投光。这个教程里我们讨论几种不同的投…...

如何使用hook?
目标:将posix函数hook住 一个简单的例子 (连接mysql服务),连接成功则打印success mysql.c #include <mysql/mysql.h> #include <stdio.h> int main(){MYSQL* mysql mysql_init(NULL);if(!mysql){printf("my…...

双指针技巧秒杀七道链表题目
文档阅读 文档阅读 题目 141. 环形链表 https://leetcode.cn/problems/linked-list-cycle/ public class Solution {public boolean hasCycle(ListNode head) {ListNode fast head, slow head;while(fast ! null && fast.next ! null){fast fast.next.next;slo…...

在“裸奔”时代保护我们的隐私:网络攻击、数据泄露与隐私侵犯的应对策略与工具
摘要:随着信息技术的普及和发展,个人隐私和数据安全问题日益受到威胁。本文将讨论如何有效应对网络攻击、数据泄露和隐私侵犯,并提供一系列实用的技巧和工具,以帮助我们在“裸奔”时代更好地保护数据安全和隐私。 当今社会&#…...

如何写出高质量代码
你是否曾经为自己写的代码而感到懊恼?你是否想过如何才能写出高质量代码?那就不要错过这个话题!在这里,我们可以讨论什么是高质量代码,如何写出高质量代码等问题。无论你是初学者还是资深开发人员,都可以在…...
[oeasy]python0048_注释_comment_设置默认编码格式
注释Comment 回忆上次内容 使用了版本控制 git 制作备份进行回滚 尝试了 嵌套的控制结构 层层 控制 不过 除非 到不得以尽量不要 太多层次的嵌套 这样 从顶到底含义 明确而且 还扁平 扁平 也能 含义明确 还可以 做点什么? 让程序含义 更加明确呢?&…...
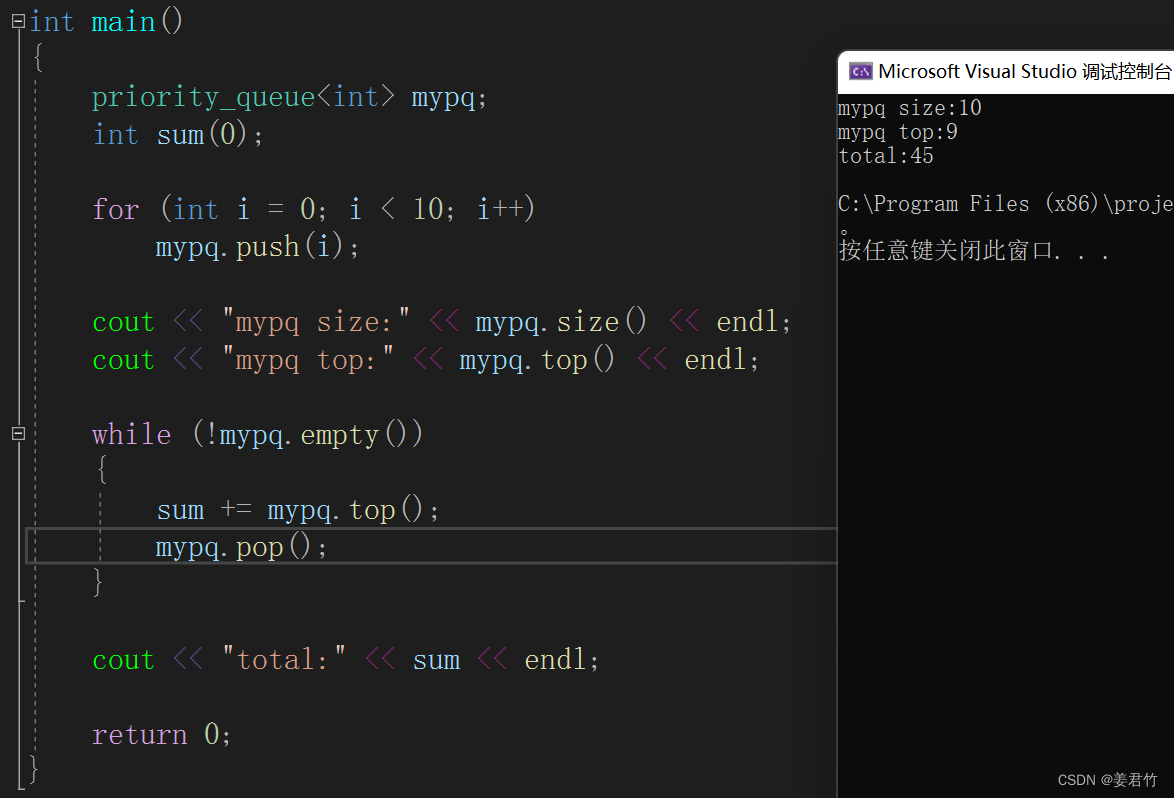
C++中的queue与priority_queue
文章目录 queuequeue的介绍queue的使用 priority_queuepriority_queue介绍priority_queue使用 queue queue的介绍 队列是一种容器适配器,专门用于上下文先进先出的操作中。队列的特性是先进先出,从容器的一端插入,另一端提取元素。 队列…...

电脑发挥极致,畅游永恒之塔sf
随着22寸显示器的普及,玩永恒之塔势必会对显示卡造成了很大负担。不要说效果全开,就连简洁的玩,都成了问题,那是不是就要重金把才买的显示卡又要拿掉呢? 最出众的解决办法,是超频。 主要就具有以下条件最佳…...
ChatGPT :十几个国内免费可用 ChatGPT 网页版
前言 ChatGPT(全名:Chat Generative Pre-trained Transformer),美国OpenAI 研发的聊天机器人程序 ,于2022年11月30日发布 。ChatGPT是人工智能技术驱动的自然语言处理工具,它能够通过理解和学习人类的语言…...
5 分钟教你如何免费用上 GPT-4
今天要分享的就是普通用户,没有 OpenAI 账号,不需要写代码,你依然可以免费体验 GPT-4,当然,会有一些缺点,本篇文章将会手把手教你怎么用上免费版的 GPT-4 以及它的一些限制。 第一步:打开 Stea…...

安卓手机搭建智能语音客服/通话播音/聊天播音乐技术实现
声明,此项技术需要root支持,如果因为刷机导致手机变砖或其他不可预料的后果请自行解决。 场景 我有一个朋友他是做业务的,主要还是做电销,其实电销相对于以前纪念没那么好做了(我自己觉得主要是互联网冲击,…...

【学习笔记】PKUSC2023 不知道咋记
挺快乐的。到 P K U PKU PKU感受了一下北大校园,其实并没有想像中那么令人惊艳,但是看到了许多亲切的学长以及他们的热心陪伴(虽然有的我甚至不认识),感觉心里还是挺暖的。 如果不算上 D 2 T 1 D2T1 D2T1被平衡树板子…...

Packet Tracer - 配置基于区域的策略防火墙 (ZPF)
Packet Tracer - 配置基于区域的策略防火墙 (ZPF) 拓扑图 地址分配表 设备 接口 IP 地址 子网掩码 默认网关 交换机端口 R1 G0/1 192.168.1.1 255.255.255.0 不适用 S1 F0/5 S0/0/0 (DCE) 10.1.1.1 255.255.255.252 不适用 不适用 R2 S0/0/0 10.1.1.2 255…...
全方位揭秘!大数据从0到1的完美落地之运行流程和分片机制
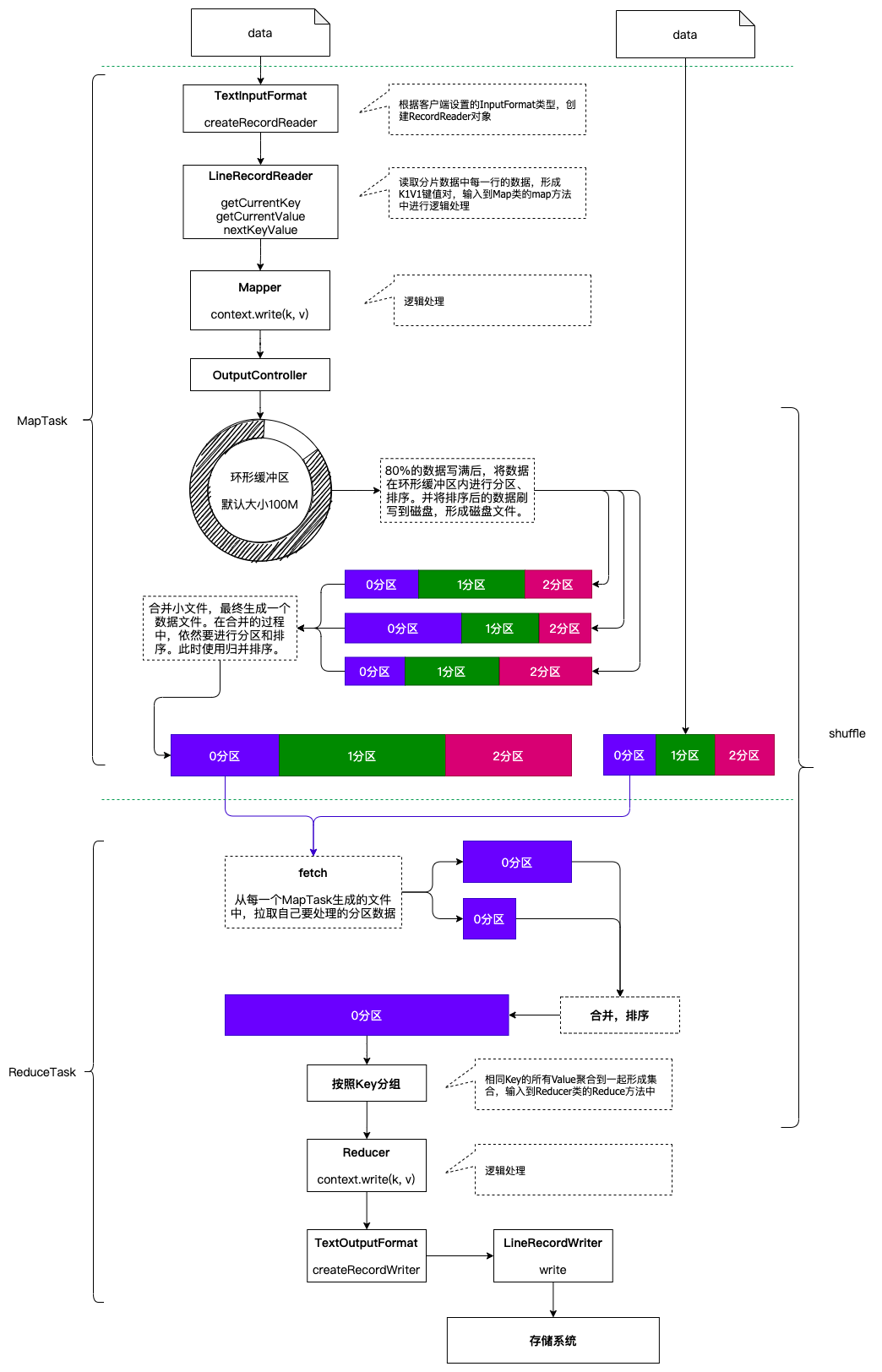
一个完整的MapReduce程序在分布式运行时有三类实例进程: MRAppMaster: 负责整个程序的过程调度及状态协调MapTask: 负责Map阶段的整个数据处理流程ReduceTask: 负责Reduce阶段的整个数据处理流程 当一个作业提交后(mr程序启动),大概流程如下࿱…...

后端程序员的前端必备【Vue】 - 07 ES6新语法
ES6新语法 1 let定义变量2 const定义常量3 模板字符串4 方法默认值5 箭头函数6 解构6.1 对象解构6.2 数组解构6.2 使用解构实现变量交换 7 Spread Operator8 模块化编程 1 let定义变量 使用let定义变量能更加精准的确定变量的作用域 //for(var i 0 ; i < 10 ; i){} for(let…...

AI落地:程序员如何用AI?
对于程序员来说,真正能提高效率、可落地的AI应用场景都有哪些? 目前已经能切实落地,融入我日常工作生活的有以下几个场景: 开发工作:自然语言生成代码,自动补全代码 日常工作学习:写作、翻译、…...

掌握优化+创新模式,轻松提升APP广告eCPM
无论是市场占有率高的综合性应用程序(App),还是透过特定目的所设计的专业化应用程序(App),内部嵌入广告已成为其主要的盈利方式。 而优化和创新作为提升广告收益的两大关键词。通过不断的数据分析和优化,结合对用户需求的深刻理解去优化和…...
在docker上安装运行Python文件
目录 一、在docker中安装python 1.1 输入镜像拉取命令 1.2 查看镜像 1.3 运行 1.4 查看是否成功 1.5 查看python版本 二、运行py文件 2.1准备运行所需文件 2.2 准备文件夹 2.3 大概是这幅模样 2.4 打包上传到服务器上 2.5 构建镜像示例 2.6 查看镜像 2.7 优化镜像的…...

RocketMQ第三节(生产者和消费者)
目录 1:生产者(同步、异步、单向) 1.1:同步发送消息(每发送一条等待mq返回值) 1.2:异步发送消息 1.3:单向发送消息(不管成功失败,只管发送消息)…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
