matlab频谱分析详解
频谱分析是一种用于分析信号频率特征的方法,常用于信号处理、音乐分析、谐波产生等领域。MATLAB是一种功能强大的数字信号处理软件,提供了许多用于频谱分析的函数和工具箱。
本文将介绍如何使用MATLAB进行频谱分析,包括信号预处理、选择合适的频谱分析方法、分析结果的可视化等内容,以便读者能够深入理解信号的频率特征特性。
一、信号预处理
在进行信号频谱分析之前,需要对信号进行预处理以获得高质量的频谱分析结果。常见的信号预处理方法包括滤波、去除噪声、平滑化、降采样等。
例如,可以使用MATLAB内置的butter函数设计高通滤波器来滤除低频噪声。具体代码如下:
fs = 1000; % 采样率为1000 Hz
order = 3; % 阶数为3阶
fc = 50; % 截止频率为50 Hz
[b, a] = butter(order, fc/(fs/2), 'high'); % 设计高通滤波器
y_filtered = filtfilt(b, a, y); % 滤波处理
二、选择合适的频谱分析方法
频谱分析方法包括快速傅里叶变换(FFT)、小波变换、模型拟合等。FFT是最常用的频谱分析方法,因为它计算速度快、易于实现。
使用MATLAB内置的fft函数可以进行FFT分析,代码如下:
Fs = 1000; % 采样率为1000 Hz
N = length(y); % 信号长度为N
Y = fft(y); % 计算FFT
f = Fs*(0:(N/2))/N; % 获取频率向量
P = abs(Y/N); % 计算幅值
P1 = P(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);
plot(f, P1) % 绘制幅度-频率图
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
在以上代码中,fs是采样率,N是输入信号的长度,Y是通过FFT计算得到的频域数据,f是频率向量,P是幅值数据。然后,我们从计算FFT后的输出数据中提取信号的幅值和频率信息,以便绘制频谱图。P1表示单侧幅值谱,即FFT计算后得到的结果的前一半。最后使用plot函数就可以绘制出数据的幅度谱(单侧频谱图)。
三、分析结果可视化
频谱分析的结果需要进行数据可视化,以便更好地理解和分析频域特征。MATLAB提供了许多绘图函数,如plot、semilogx、semilogy、loglog等,可以用于绘制频谱图。
例如,使用plot函数绘制信号的单侧幅值谱图,代码如下:
plot(f,P1); % 绘制频谱图
xlabel('频率(Hz)'); % 添加坐标轴标签
ylabel('幅度');
title('信号频率幅值谱图');
使用semilogx函数绘制包络值图,代码如下:
semilogx(f, 10*log10(P1),'r','LineWidth',2);
grid on;
xlabel('频率(Hz)'); % 添加坐标轴标签
ylabel('功率(dB)');
title('信号功率频谱覆盖值图');
使用imagesc函数绘制增益、时间和频率的三维图形,代码如下:
[s,f,t,p] = spectrogram(x,hanning(128),120,1024,fs,'yaxis');
imagesc(t,f,10*log10(p)),axis xy;
xlabel('Time(s)'),ylabel('Frequency(Hz)')
以上就是MATLAB频谱分析的具体操作步骤和代码实现,在这个过程中,我们需要注意充分了解信号特征,选择合适的预处理方法和分析方法,并使用适当的绘图函数来展示分析结果。
综上所述,本文介绍了MATLAB进行频谱分析的基本方法和技巧,希望对信号处理和音频分析领域的专业人士和科研工作者提供一些有用的参考和指导。
相关文章:

matlab频谱分析详解
频谱分析是一种用于分析信号频率特征的方法,常用于信号处理、音乐分析、谐波产生等领域。MATLAB是一种功能强大的数字信号处理软件,提供了许多用于频谱分析的函数和工具箱。 本文将介绍如何使用MATLAB进行频谱分析,包括信号预处理、选择合适…...

用layui写用户登录页面遇到的问题
用layui写用户登录页面遇到的问题 1.在layui-row下面的layui-col-md还是换行 原因:link标签和script标签中的type属性没写,导致应该是script或者这个css没有识别出来 解决办法:link标签里面加上type为text/css, script标签中加上type为 2…...
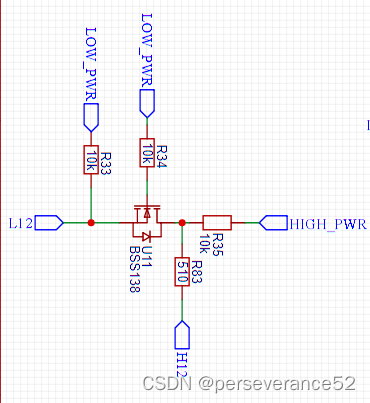
NMOS双向转换电路实测以及上升沿尖峰处理
NMOS双向转换电路实测以及上升沿尖峰处理 NMOS双向转换电路 🔧采用的是5V供电的STC8H单片机输出PWM波形,经过上面的电平转换电路测量低压端的波形。 ✨在做3.3V <>5V 电平转换电路方案验证时,输入5V PWM波形和输出波形的波形上升沿有尖…...
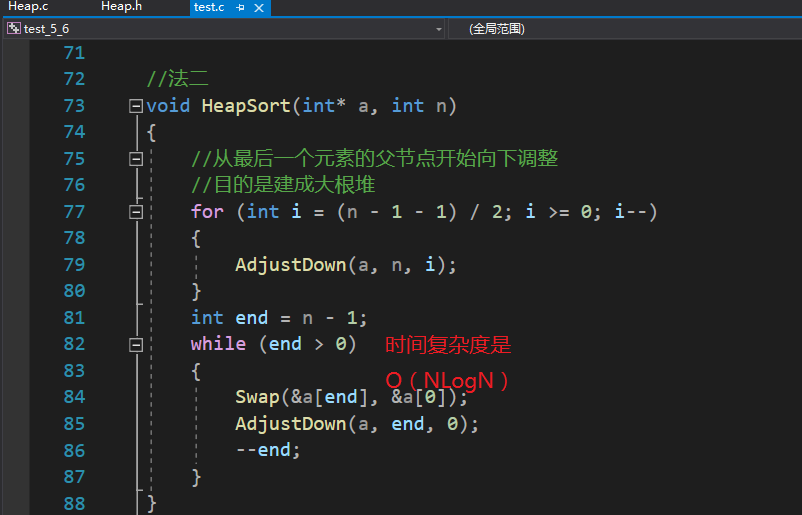
【数据结构】选择排序(详细)
选择排序 1. 直接选择排序2. 堆排序2.1 堆2.2 堆的实现(以大根堆为例)2.3 堆排序 3. 堆排序(topK问题) 1. 直接选择排序 思想 以排升序为例。以a[i]为最大值(或最小值),从a[i1]到a[n-1-i]比较选…...

什么是企业内容管理?
为什么出现企业内容管理? 在数字经济的宏观背景下,企业建立了各种应用系统以满足企业各业务的管理需求,这些系统每天都在产生大量的数据和信息资源,但在企业实践中存在很多数据或资源无法被应用系统获取、处理和共享。 比如发票…...

机器学习:分类、回归、决策树
分类:具有明确的类别 如:去银行借钱,会有借或者不借的两种类别 回归:不具有明确的类别和数值 如:去银行借钱,预测银行会借给我多少钱,如:1~100000之间的一个数值 不纯度࿱…...

java常见的异常,下一篇写如何正确处理异常
当我们编写Java程序时,经常会遇到各种异常情况。异常是指在程序执行过程中发生的一些错误或意外情况,它会打断程序的正常执行流程,并且需要被适当地处理。在Java中,异常被分为两种类型:可检查异常(Checked …...

C#开发的OpenRA游戏之网络协议打包和解包
C#开发的OpenRA游戏之网络协议打包和解包 OpenRA游戏里,由于这是一个网络游戏,那么与服务器通讯就缺少不了, 既然要通讯,那么就需要协议,有协议就需要对数据进行打包和解包, 这个过程其实就是序列化与反序列化的过程。 游戏里很多命令都需要发送给服务器,以便服务器同…...

K8S通过Ansible安装集群
K8S通过Ansible安装集群 K8S集群安装可参考https://gitee.com/open-hand/kubeadm-ha.git、https://github.com/easzlab/kubeasz.git 安装高可用集群 git clone https://gitee.com/open-hand/kubeadm-ha.git && cd kubeadm-ha升级内核,非必需,默认不升级&…...

ChatGPT辩证观点:“人才不是一个企业的核心竞争力,对人才的管理能力才是一个企业的核心竞争力”
一、问: “人才不是一个企业的核心竞争力,对人才的管理能力才是一个企业的核心竞争力”这句话的理解和误解,这句话有哪个中心论点转移和变化 二、ChatGPT答: 这句话的理解和误解: 理解:这句话的意思是说…...

windows11 永久关闭windows defender的方法
1、按键盘上的windows按键,再点【设置】选项。 2、点击左侧菜单的【隐私和安全性】,再点击列表的【Windows安全中心】选项。 3、点击界面的【病毒和威胁保护】设置项。 4、病毒保护的全部关闭 5、别人的图(正常是都开着的) 6、终极…...

继承的基本知识
概念 假设基于A类,创建了B类,那么称A为B的父类,B为A的子类 子类会继承父类的成员变量及成员函数,但是不能继承构造、析构、运算符重载 假设又基于B创建了C,那么称B为C的直接基类,A为C的间接基类 继承按…...
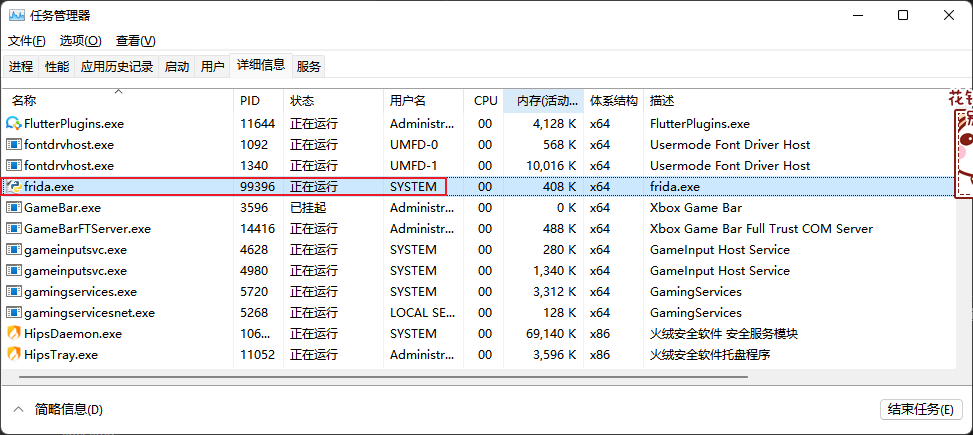
【Frida-实战】EA游戏平台的文件监控(PsExec.exe提权)
▒ 目录 ▒ 🛫 问题描述环境 1️⃣ 代码编写开源代码搜索自己撸代码procexp确定句柄对应的文件名并过滤 2️⃣ PsExec.exe提权定位找不到EABackgroundService.exe的问题 PsExec.exe提权PsExec.exe原理 🛬 结论📖 参考资料 🛫 问题…...

可视化和回归分析星巴克咖啡在中国的定价建议
可视化和回归分析星巴克咖啡在中国的定价建议。星巴克的拿铁大杯Tall 在各国的价格。 Claude AI | 代码自动生成的数据可视化代码 选择Claude AI 而非 ChatGPT的理由是前者更懂中文!具体可以参见我前面的两篇文章对比两者的中英文翻译的表现及使用安装等难易程度…...

热门影片怎么买票比较便宜,低价买电影票的方法,纯攻略!
有时候真的有被自己蠢到!看电影看了这么多年,竟然不知道电影票价格才9.9元、19.9元就能买到。之前我看电影动不动就是几十上百块,感觉好亏啊。 其实,我也不敢相信的,通过这些平台,同时在节假日甚至春节档期…...

Python通过SWIG调用C++时出现的ImportError问题解析
摘要 win10系统,编译器为mingw,按照教程封装C的一个类并用python调用,一步步进行直到最后一步运行python代码时,在python代码中import example时报错ImportError: DLL load failed while importing _example: The specified modul…...

3ds Max云渲染有多快,3ds Max云渲染怎么用?
本地渲染效果图和动画3D项目是一个非常耗时的过程,当在场景中使用未优化的几何体或在最终渲染中使用大量多边形模型时,诸如此类的变量最终会增加渲染项目所需的时间和处理器能力。随着提供的渲染服务的云渲染平台出现,越来越多动画师、艺术家…...

Java之线程安全
目录 一.上节回顾 1.Thread类常见的属性 2.Thread类中的方法 二.多线程带来的风险 1.观察线程不安全的现象 三.造成线程不安全现象的原因 1.多个线程修改了同一个共享变量 2.线程是抢占式执行的 3.原子性 4.内存可见性 5.有序性 四.解决线程不安全问题 ---synchroni…...

我有一个方法判断你有没有编程天赋
我有一个方法判断你有没有编程天赋 一 前言 基于知识的诅咒的原理 做一个敲击者很难。问题在于敲击者已拥有的知识(歌曲题目)让 他们想象不到缺乏这种知识会是什么情形。当他们敲击的时候,他 们不能想象听众听到的是那些独立的敲击声而不是…...

python 生成chart 并以附件形式发送邮件
import requests import json import pandas as pd import numpy as np import matplotlib.pyplot as plt data np.random.randn(5, 3)#生成chart def generate_line_chart(data):df pd.DataFrame(np.abs(data),index[Mon, Tue, Wen, Thir, Fri],columns[A, B, C])df.plot()…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
