数据结构刷题(三十一):1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II
一、1049. 最后一块石头的重量 II
1.思路:01背包问题,其中dp[j]表示容量为j的背包,最多可以背最大重量为dp[j]。
2.注意:递推公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);本题中的重量就是价值,所以第二个stone[i]表示价值的意思; 遍历顺序上仍然是先物品后背包
3.本题与分割等和子集类似,不同就在于最后return时,本题得到的target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]。
所以相撞也就是将target与sum - dp[target]作差即可。
class Solution {public int lastStoneWeightII(int[] stones) {if (stones.length == 0 || stones == null)return 0;int sum = 0;// 先求出这堆石头的和,以便得到背包能背的最大重量for (int stone : stones) {sum += stone;}int target = sum >> 1;int[] dp = new int[target + 1];// for循环, 先物品再背包for (int i = 0; i < stones.length; i++) {// 这里的内循环一定是j >= stone[i] ,否则无法判断第二个max条件for (int j = target; j >= stones[i]; j--){dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}二、完全背包
1.有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
2.核心代码:区别于01背包的一维滚动数组,差别就是内循环
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}3.计算过程

3.518. 零钱兑换 II
1.思路:完全背包。
2.递推公式:dp[j] += dp[j - nums[i]],表示填满j(包括j)这么大容积的包,有dp[j]种方法。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
3.注意:该题纯完全背包是能凑成总和就行,不用管怎么凑的,不需要管顺序。
4.代码:
class Solution {public int change(int amount, int[] coins) {// dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法int[] dp = new int[amount+1];//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装dp[0] = 1;for (int i = 0; i < coins.length; i++) { // 零钱的种类数for (int j = coins[i]; j <= amount; j++){ // 组合方法dp[j] += dp[j - coins[i]];}}return dp[amount];}
}相关文章:

数据结构刷题(三十一):1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II
一、1049. 最后一块石头的重量 II 1.思路:01背包问题,其中dp[j]表示容量为j的背包,最多可以背最大重量为dp[j]。 2.注意:递推公式dp[j] max(dp[j], dp[j - stones[i]] stones[i]);本题中的重量就是价值,所以第二个…...

opencv_c++学习(四)
图像在opencv中的存储方式 在上图中可以看出,在opencv中采用的是像素值来代表每一个像素三通道颜色的深浅。 Mat对象 Mat对象是在OpenCV2.0之后引进的图像数据结构、自动分配内存、不存在内存泄漏的问题,是面向对象的数据结构。分了两个部分࿰…...

基于AT89C51单片机的篮球计时记分设计
点击链接获取Keil源码与Project Backups仿真图: https://download.csdn.net/download/qq_64505944/87771065 源码获取 主要内容: 基于51单片机设计篮球计时计分器,结合单片机串行接口原理,用AT89C51设计一个篮球比赛计分计时器,能够通过数码管显示分数和比赛时间(并设有…...

并发编程-Day2
并发编程 1.共享模型-内存 共享变量在多线程间的<可见性>问题与多条指令执行时的<有序性>问题 1.1Java内存模型 JMM它定义了主存、工作内存抽象概念,底层对应着CPU寄存器、缓存、硬件内存CPU指令优化等. JMM体现在: 原子性-保证指令不会受到线程上…...

第1章 Nginx简介
基于 Nginx版本 1.14.2 ,Tomcat版本 9.0.0 演示 第1章 Nginx简介 1.1 Nginx发展介绍 Nginx (engine x) 是一个高性能的Web服务器和反向代理服务器,也可以作为邮件代理服务器。 Nginx 特点是占有内存少,并发处理能力…...
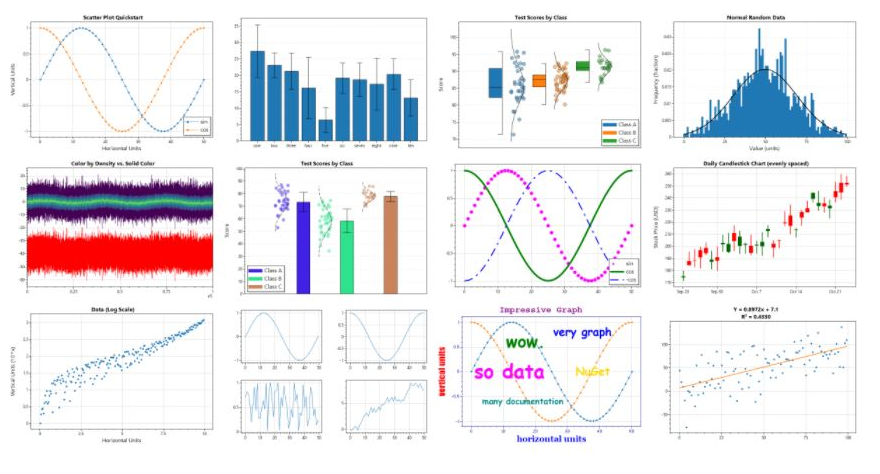
一个.Net功能强大、易于使用、跨平台开源可视化图表
可视化图表运用是非常广泛的,比如BI系统、报表统计等。但是针对桌面应用的应用,很多报表都是收费的,今天给大家推荐一个免费.Net可视化开源的项目! 项目简介 基于C#开发的功能强大、易于使用、跨平台高质量的可视化图表库&#…...

浅谈 ext2 文件系统的特点、优缺点以及使用场景
ext2(Extended File System 2)是 Linux 中最早的一种文件系统,它是 Linux 文件系统的基础,也被广泛用于其他类 Unix 系统中。下面是 ext2 文件系统的特点、优缺点以及使用场景: 特点: ext2 文件系统可以支…...

Map和Set数据结构和ES6模块化语法
Map和Set数据结构 ●ES6 新增的两种数据结构 ●共同的特点: 不接受重复数据 Set数据结构 ●是一个 类似于 数组的数据结构 ●按照索引排列的数据结构 创建 Set 数据结构 语法: var s new Set([ 数据1, 数据2, 数据3, ... ]) Set 数据结构的属性和方法 ●size 属性 ○语法: 数…...

10_Uboot启动流程_2
目录 _main函数详解 board_init_f函数详解 relocate_code函数详解 relocate_vectors函数详解 board_init_r 函数详解 _main函数详解 在上一章得知会执行_main函数_main函数定义在文件arch/arm/lib/crt0.S 中,函数内容如下: 第76行,设置sp指针为CONFIG_SYS_INIT_SP_ADDR,也…...
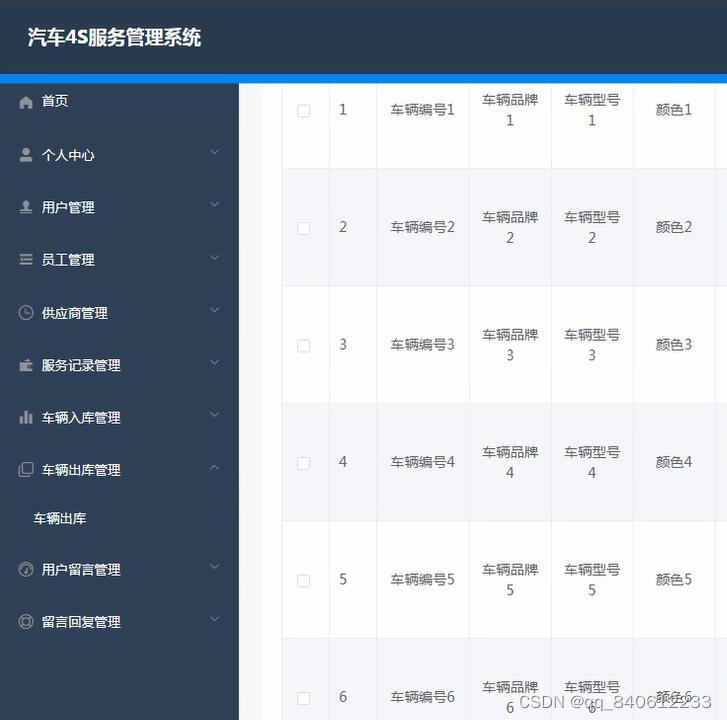
python+django汽车4S店零配件保养服务管理系统
汽车4S服务管理系统包括三种用户。管理员、普通员工、客户。 开发语言:Python 框架:django/flask Python版本:python3.7.7 数据库:mysql 数据库工具:Navicat 开发软件:PyCharm django 应用目录结构管…...

STM32F4的输出比较极性和PWM1,PWM2的关系
PWM 输出比较通道 在这里以通用定时器的通道1作为介绍。 如图,左边就是CNT计数器和CCR1第一路的捕获/比较寄存器,它俩进行比较,当CNT>CCR1, 或者CNTCCR1时,就会给输出模式控制器传送一个信号,然后输出模式控制器就…...

易优cms伪静态,EyouCms去除URL中的index.php
针对不同服务器、虚拟空间,运行PHP的环境也有所不同,目前主要分为:Nginx、apache、IIS以及其他服务器。下面分享如何去掉URL上的index.php字符,记得在管理后台清除缓存,对于一些ECS服务器可能要重启nginx等服务! 【Nginx服务器】 在原有的nginx重写文件里新增以下代码片…...
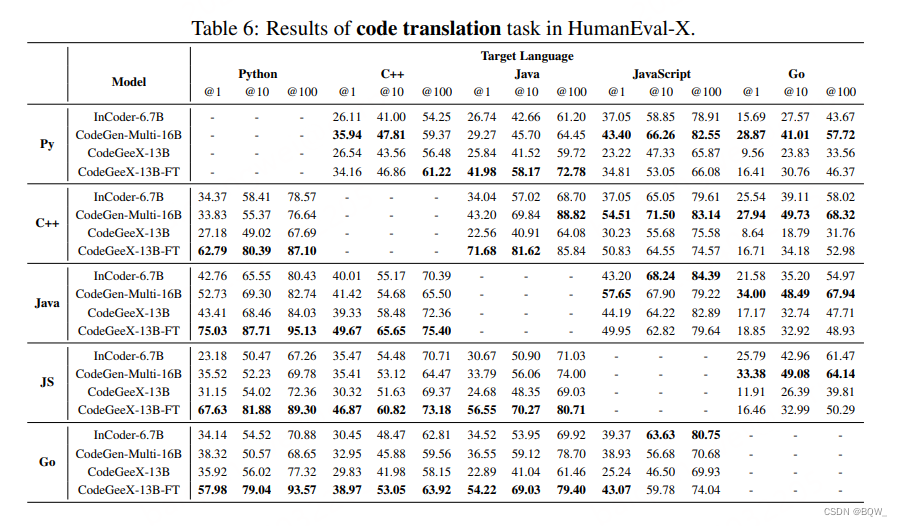
【自然语言处理】【大模型】CodeGeeX:用于代码生成的多语言预训练模型
CodeGeeX:用于代码生成的多语言预训练模型 《CodeGeeX: A Pre-Trained Model for Code Generation with Multilingual Evaluations on HumanEval-X》 论文地址:https://arxiv.org/pdf/2303.17568.pdf 相关博客 【自然语言处理】【大模型】CodeGen&#x…...

Open3D 非线性最小二乘拟合二维多项式曲线
目录 一、算法原理二、代码实现三、结果展示一、算法原理 多项式曲线表示为: p ( x ) = p 1 x n + p 2 x n...

kafka消息队列的两种模式
第一种模式: 点对点模式(一对一,消费者主动拉取数据,消息收到后消息清除) 1.消息生产者生产消息发送给队列,然后消费者从队列中取出并且消费消息 2.消息被消费以后,queue中不再有存储࿰…...
python语法复习
print:输出函数 print(520)效果:输出520. print(hello)效果:输出hello. print(1020)【效果:输出了:1020】注:“ ”在print里面是一个连接符。 print(1020)【效果:输出了30】注: 在此处…...
02-Java基础编程
Java基础编程 Java 基础语法Java 标识符变量变量的类型Java 基本数据类型基本数据类型转换 运算符常见运算符运算符的优先级 程序流程控制分支语句循环结构常用的循环结构循环的嵌套break 和 continue 关键字 数组一维数组多维数组的使用Arrays 工具类的使用数组中常见的异常 J…...
)
武忠祥老师每日一题||定积分基础训练(十)
已知f(x)连续 ∫ 0 x t f ( x − t ) d t 1 − cos x , 求 ∫ 0 π 2 f ( x ) d x 的值。 \int_{0}^{x}tf(x-t)\,{\rm d}t1-\cos x,求\int_{0}^{\frac{\pi}{2}}f(x)dx的值。 ∫0xtf(x−t)dt1−cosx,求∫02πf(x)dx的值。 已知一个关于f的变上限积分等式,&…...
)
C/C++趣味程序设计百例(41~50)
C/C语言经典、实用、趣味程序设计编程百例精解(5) 41.马克思手稿中的数学题 马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,在一家饭馆吃饭花了50先令;每个男人花3先令,每个…...

论文阅读-2-DeepSMOTE Fusing Deep Learning and SMOTE for Imbalanced Data
文章目录 Abstract1. Introduction2. Learning From Imbalanced Data1. 数据级2. 算法级3. 集成方法 3. Deep Learning From Imbalanced Data基于深度神经网络的实例生成损失函数适应长尾识别 4. DeepSMOTEA. 动机B. 描述C. encoder-decoder框架D. 增强的损失函数E. 人工图像生…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
