武忠祥老师每日一题||定积分基础训练(十)
已知f(x)连续 ∫ 0 x t f ( x − t ) d t = 1 − cos x , 求 ∫ 0 π 2 f ( x ) d x 的值。 \int_{0}^{x}tf(x-t)\,{\rm d}t=1-\cos x,求\int_{0}^{\frac{\pi}{2}}f(x)dx的值。 ∫0xtf(x−t)dt=1−cosx,求∫02πf(x)dx的值。
已知一个关于f的变上限积分等式,(变上限积分函数的特点,求导比较容易)所以可以等式两边同时求导。
但是对于这个题目,不可以直接求导。在变上限函数中,t是积分变量,而x不是。
对于这类题目,有一个通用方法----做变量代换,把x-t换成变量u。
❗❗❗变量代换注意换上下限,下面容易出错!
令u=x-t <=> t=x-u
d t = − d u , 但是当发生变量代换时: t = 0 , u = 0 ; t = x , u = − x dt=-du,但是当发生变量代换时:t=0,u=0;\\t=x,u=-x dt=−du,但是当发生变量代换时:t=0,u=0;t=x,u=−x
这时原式 = − ∫ 0 − x ( x − u ) f ( u ) d u = ∫ 0 x ( x − u ) f ( u ) d u 这时原式=-\int_{0}^{-x}(x-u)f(u)du=\int_{0}^{x}(x-u)f(u)du 这时原式=−∫0−x(x−u)f(u)du=∫0x(x−u)f(u)du
原式= ∫ 0 x ( x − u ) f ( u ) d u \int_{0}^{x}(x-u)f(u)du ∫0x(x−u)f(u)du
= x ∫ 0 x f ( u ) d u − ∫ 0 x u f ( u ) d u =x\int_{0}^{x}f(u)du-\int_{0}^{x}uf(u)du =x∫0xf(u)du−∫0xuf(u)du
对等式两边同时求导得,
∫ 0 x f ( u ) d u + x f ( x ) − x f ( x ) = sin x \int_{0}^{x}f(u)du+xf(x)-xf(x)=\sin x ∫0xf(u)du+xf(x)−xf(x)=sinx
即 ∫ 0 x f ( u ) d u = sin x \int_{0}^{x}f(u)du=\sin x ∫0xf(u)du=sinx
这时对等式两边再次同时求导,得
f ( x ) = cos x f(x)=\cos x f(x)=cosx
这时,题目要求的
∫ 0 π 2 f ( x ) d x \int_{0}^{\frac{\pi}{2}}f(x)dx ∫02πf(x)dx
= ∫ 0 π 2 cos x d x =\int_{0}^{\frac{\pi}{2}}\cos x dx =∫02πcosxdx
= sin x ∣ 0 π 2 = 1 =\sin x |_{0}^{\frac{\pi}{2}}=1 =sinx∣02π=1
相关文章:
)
武忠祥老师每日一题||定积分基础训练(十)
已知f(x)连续 ∫ 0 x t f ( x − t ) d t 1 − cos x , 求 ∫ 0 π 2 f ( x ) d x 的值。 \int_{0}^{x}tf(x-t)\,{\rm d}t1-\cos x,求\int_{0}^{\frac{\pi}{2}}f(x)dx的值。 ∫0xtf(x−t)dt1−cosx,求∫02πf(x)dx的值。 已知一个关于f的变上限积分等式,&…...
)
C/C++趣味程序设计百例(41~50)
C/C语言经典、实用、趣味程序设计编程百例精解(5) 41.马克思手稿中的数学题 马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,在一家饭馆吃饭花了50先令;每个男人花3先令,每个…...

论文阅读-2-DeepSMOTE Fusing Deep Learning and SMOTE for Imbalanced Data
文章目录 Abstract1. Introduction2. Learning From Imbalanced Data1. 数据级2. 算法级3. 集成方法 3. Deep Learning From Imbalanced Data基于深度神经网络的实例生成损失函数适应长尾识别 4. DeepSMOTEA. 动机B. 描述C. encoder-decoder框架D. 增强的损失函数E. 人工图像生…...
三种方法教你让模糊照片秒变高清图
现在随着数字相机和智能手机的普及,我们拍摄的照片数量越来越多,但是有些照片可能因为环境或技术等原因导致模糊不清,这时候我们就需要使用一些软件或工具来让照片变得清晰,以满足我们的需求。 下面介绍三种常用的照片变清晰的方…...
PyTorch深度学习实战 | 基于线性回归、决策树和SVM进行鸢尾花分类
鸢尾花数据集是机器学习领域非常经典的一个分类任务数据集。它的英文名称为Iris Data Set,使用sklearn库可以直接下载并导入该数据集。数据集总共包含150行数据,每一行数据由4个特征值及一个标签组成。标签为三种不同类别的鸢尾花,分别为&…...
服务端接口优化方案
一、背景 针对老项目,去年做了许多降本增效的事情,其中发现最多的就是接口耗时过长的问题,就集中搞了一次接口性能优化。本文将给小伙伴们分享一下接口优化的通用方案。 二、接口优化方案总结 1. 批处理 批量思想:批量操作数据…...

【并发基础】Happens-Before模型详解
目录 一、Happens-Before模型简介 二、组成Happens-Before模型的八种规则 2.1 程序顺序规则(as-if-serial语义) 2.2 传递性规则 2.3 volatile变量规则 2.4 监视器锁规则 2.5 start规则 2.6 Join规则 一、Happens-Before模型简介 除了显示引用vo…...

Kubernetes系列---Kubernetes 理论知识 | 初识
Kubernetes系列---Kubernetes 理论知识 | 初识 1.K8s 是什么?2.K8s 特性3.小拓展(业务升级)4.K8s 集群架构与组件①架构拓扑图:②Master 组件③Node 组件 五 K8s 核心概念六 官方提供的三种部署方式总结 1.K8s 是什么?…...

KingbaseES 原生XML系列三--XML数据查询函数
KingbaseES 原生XML系列三--XML数据查询函数(EXTRACT,EXTRACTVALUE,EXISTSNODE,XPATH,XPATH_EXISTS,XMLEXISTS) XML的简单使其易于在任何应用程序中读写数据,这使XML很快成为数据交换的一种公共语言。在不同平台下产生的信息,可以很容易加载XML数据到程序…...
【51单片机】点亮一个LED灯(看开发板原理图十分重要)
🎊专栏【51单片机】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【The Right Path】 🥰大一同学小吉,欢迎并且感谢大家指出我的问题🥰 目录 🍔基础内容 🏳…...
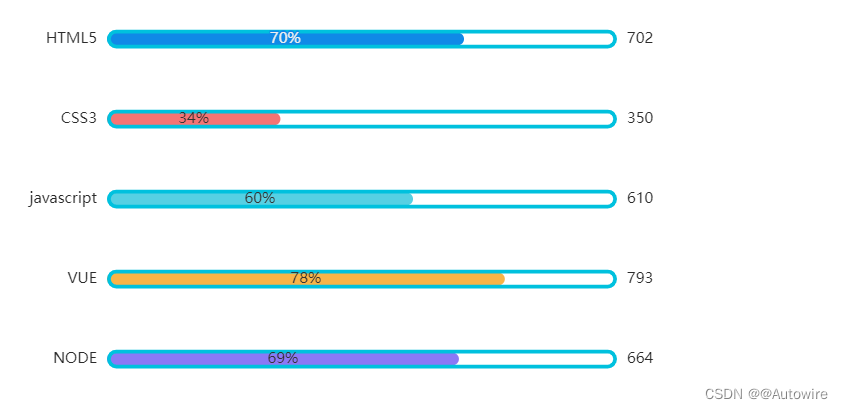
数据可视化工具 - ECharts以及柱状图的编写
1 快速上手 引入echarts 插件文件到html页面中 <head><meta charset"utf-8"/><title>ECharts</title><!-- step1 引入刚刚下载的 ECharts 文件 --><script src"./echarts.js"></script> </head>准备一个…...
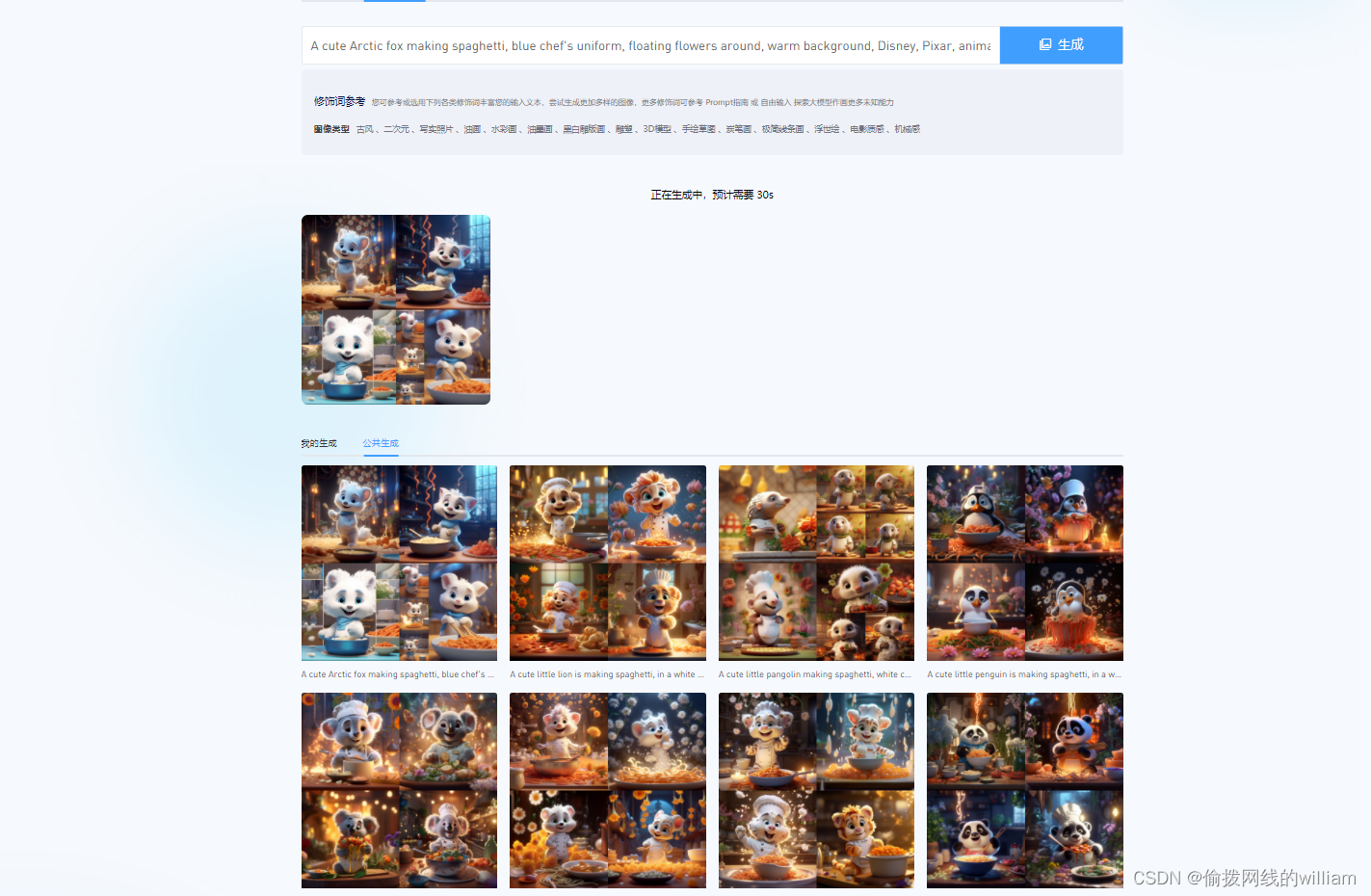
【AI绘画】——Midjourney关键词格式解析(常用参数分享)
目前在AI绘画模型中,Midjourney的效果是公认的top级别,但同时也是相对较难使用的,对小白来说比较难上手,主要就在于Mj没有webui,不能选择参数,怎么找到这些隐藏参数并且触发它是用好Mj的第一步。 今天就来…...

操作符知识点大全(简洁,全面,含使用场景,演示,代码)
目录 一.算术操作符 1.要点: 二.负数原码,反码,补码的互推 1.按位取反操作符:~(二进制位) 2.原反补互推演示 三.进制位的表示 1.不同进制位的特征: 2.二进制位表示 3.整型的二进制表…...

华工研究生语音课
这门课讲啥 语音蕴含的信息、语音识别的目的 语音的准平稳性、分帧、预加重、时域特征分析(能量和过零率)、端点检测(双门限法) 语音的基频及检测(主要是自相关法、野点的处理) 声音的产生过程…...

KingbaseES 原生XML系列二 -- XML数据操作函数
KingbaseES 原生XML系列二--XML数据操作函数(DELETEXML,APPENDCHILDXML,INSERTCHILDXML,INSERTCHILDXMLAFTER,INSERTCHILDXMLBEFORE,INSERTXMLAFTER,INSERTXMLBEFORE,UPDATEXML) XML的简单使其易于在任何应用程序中读写数据,这使XML很快成为数据交换的一种公共语言。…...
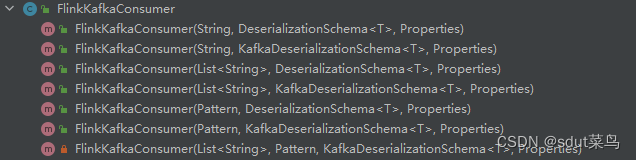
【Flink】DataStream API使用之源算子(Source)
源算子 创建环境之后,就可以构建数据的业务处理逻辑了,Flink可以从各种来源获取数据,然后构建DataStream进项转换。一般将数据的输入来源称为数据源(data source),而读取数据的算子就叫做源算子(…...
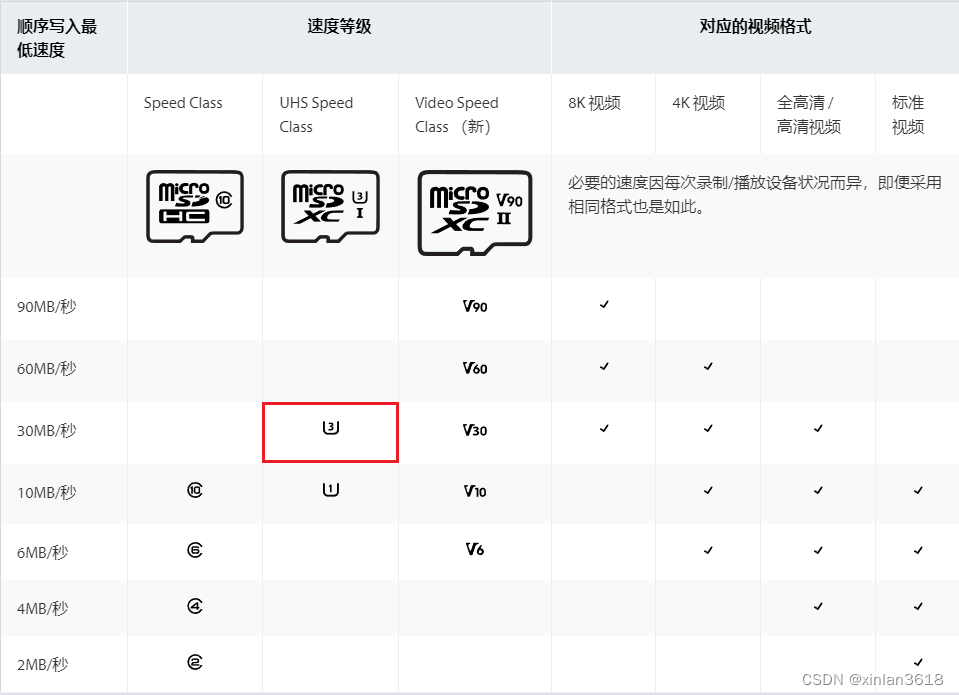
树莓派硬件介绍及配件选择
目录 树莓派Datasheet下载地址: Raspberry 4B 外观图: 技术规格书: 性能介绍: 树莓派配件选用 电源的选用: 树莓派外壳选用: 内存卡/U盘选用 树莓派Datasheet下载地址: Raspberry Pi …...
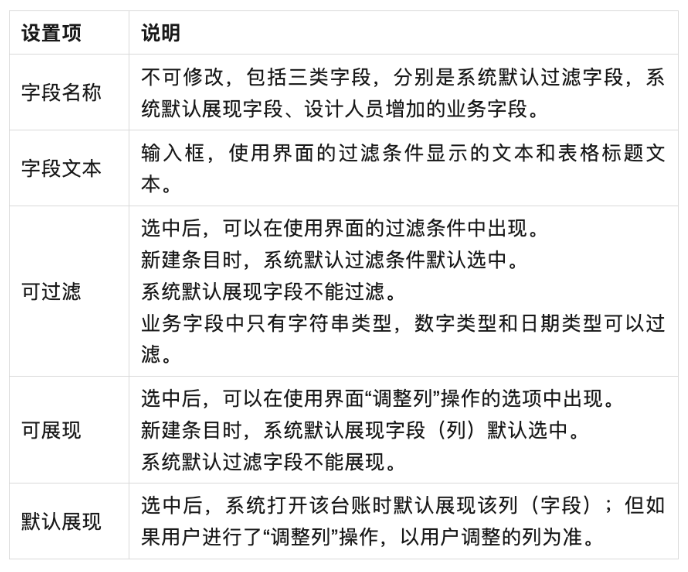
O2OA (翱途) 平台 V8.0 发布新增数据台账能力
亲爱的小伙伴们,O2OA (翱途) 平台开发团队经过几个月的持续努力,实现功能的新增、优化以及问题的修复。2023 年度 V8.0 版本已正式发布。欢迎大家到 O2OA 的官网上下载进行体验,也希望大家在藕粉社区里多提宝贵建议。本篇我们先为大家介绍应用…...

数控解锁怎么解 数控系统解锁解密
Amazon Fargate 在中国区正式落地,因 数控解锁使用 Serverless 架构,更加适合对性能要求不敏感的服务使用,Pyroscope 是一款基于 Golang 开发的应用程序性能分析工具,Pyroscope 的服务端为无状态服务且性能要求不敏感,…...
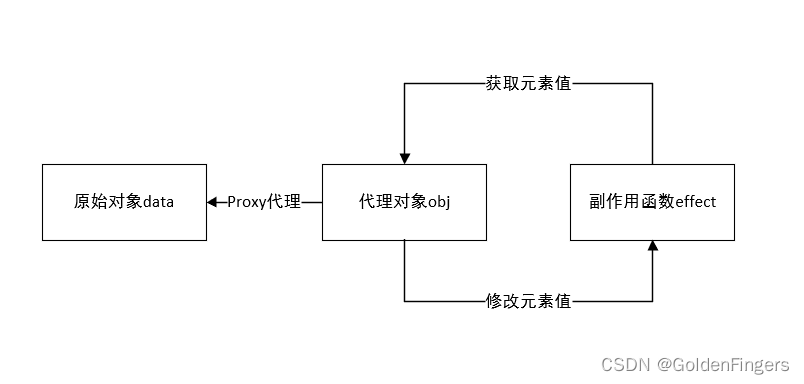
3.0 响应式系统的设计与实现
1、Proxy代理对象 Proxy用于对一个普通对象代理,实现对象的拦截和自定义,如拦截其赋值、枚举、函数调用等。里面包含了很多组捕获器(trap),在代理对象执行相应的操作时捕获,然后在内部实现自定义。 const…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
