【结构与算法】—— 游戏概率常用算法整理 | 游戏中的常见概率设计分析

- 📢博客主页:肩匣与橘
- 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!
- 📢本文由肩匣与橘编写,首发于CSDN🙉
- 📢生活依旧是美好而又温柔的,你也是✨
目录
一、随机数生成
二、概率分布
2.1均匀分布
2.2正态分布
2.3泊松分布
三、随机事件触发
3.1固定概率触发
3.2基于概率分布的触发
3.3基于条件的触发
四、常见概率算法
4.1概率表
4.2权重随机
4.3概率分布函数
五、真随机和伪随机
在游戏开发中,概率技术是非常重要的一部分。它涉及到游戏中的随机事件,如掉落物品、怪物出现、技能触发等。正确使用概率技术可以使游戏更加有趣和具有挑战性。
一、随机数生成
在游戏中,随机数生成是非常常见的。我们需要生成随机数来模拟各种随机事件。在C++中,我们可以使用rand函数来生成随机数。rand函数返回一个介于0和RAND_MAX(通常是32767)之间的整数。我们可以使用模运算和加法来生成指定范围内的随机数。 例如,我们要生成1到100之间的随机数,可以使用以下代码:
int randomNumber = rand() % 100 + 1;二、概率分布
在游戏中,我们经常需要使用不同的概率分布来模拟各种随机事件。以下是一些常见的概率分布:
2.1均匀分布
均匀分布是最基本的概率分布之一。在均匀分布中,每个数字出现的概率是相等的。我们可以使用rand函数来生成均匀分布。 例如,我们要生成1到6之间的随机数,可以使用以下代码:
int randomNumber = rand() % 6 + 1;2.2正态分布
正态分布是另一个常见的概率分布。在正态分布中,大多数数字集中在平均值附近,并且随着距离平均值的增加而变得越来越少。我们可以使用Box-Muller转换来生成正态分布。 以下是一个生成具有指定平均值和标准差的正态分布的代码示例:
double normalRandomNumber(double mean, double stddev)
{static double n2 = 0.0;static int n2_cached = 0;if (!n2_cached){double x, y, r;do{x = 2.0*rand()/RAND_MAX - 1;y = 2.0*rand()/RAND_MAX - 1;r = x*x + y*y;}while (r == 0.0 || r > 1.0);{double d = sqrt(-2.0*log(r)/r);double n1 = x*d;n2 = y*d;double result = n1*stddev + mean;n2_cached = 1;return result;}}else{n2_cached = 0;return n2*stddev + mean;}
}2.3泊松分布
泊松分布是用于模拟随机事件发生的数量的分布。在泊松分布中,事件发生的概率是相等的,而事件发生的次数是随机的。我们可以使用以下代码来生成泊松分布:
int poissonRandomNumber(double lambda)
{double L = exp(-lambda);double p = 1.0;int k = 0;do{k++;double u = rand()/((double)RAND_MAX + 1);p *= u;}while (p > L);return k - 1;
}三、随机事件触发
在游戏中,我们经常需要触发各种随机事件,如掉落物品、怪物出现、技能触发等。我们可以使用概率技术来控制这些事件的触发概率。以下是一些常见的随机事件触发技术:
3.1固定概率触发
在固定概率触发中,我们使用一个固定的概率来控制事件的触发。例如,我们可以使用以下代码来控制一个事件以50%的概率触发:
bool shouldTrigger = (rand() % 2 == 0);
if (shouldTrigger)
{// 触发事件
}3.2基于概率分布的触发
在基于概率分布的触发中,我们使用一个特定的概率分布来控制事件的触发。例如,我们可以使用以下代码来控制一个事件以正态分布的概率触发:
double mean = 0.5;
double stddev = 0.1;
double randomNumber = normalRandomNumber(mean, stddev);
if (randomNumber > 0 && randomNumber < 1)
{// 触发事件
}3.3基于条件的触发
在基于条件的触发中,我们使用一个或多个条件来控制事件的触发。例如,我们可以使用以下代码来控制一个事件仅在满足一定条件时触发:
bool condition1 = true;
bool condition2 = false;
if (condition1 && !condition2)
{// 触发事件
}四、常见概率算法
4.1概率表
概率表是一种最简单的概率算法。它将所有的可能结果列出,并为每个结果分配一个概率值。然后,使用随机数生成器来生成一个随机数,并根据随机数选择一个结果。 例如,我们有一个掉落物品的概率表,其中掉落物品的概率分别为30%、20%和10%:
| 物品 | 概率 |
|---|---|
| 物品A | 30% |
| 物品B | 20% |
| 物品C | 10% |
我们可以使用随机数生成器来生成一个随机数,例如在Java中,我们可以使用以下代码:
import java.util.Random;
public class Example {public static void main(String[] args) {Random random = new Random();// 生成一个随机整数int randomInt = random.nextInt(100);// 判断掉落的物品if (randomInt < 30) {// 掉落物品A} else if (randomInt < 50) {// 掉落物品B} else {// 掉落物品C}}
}上述代码中,我们生成一个0到99的随机整数,并根据随机数选择掉落的物品。
4.2权重随机
权重随机是一种更加高级的概率算法。它将所有的可能结果列出,并为每个结果分配一个权重值。然后,使用随机数生成器来生成一个随机数,并根据权重值选择一个结果。 例如,我们有一个掉落物品的权重表,其中掉落物品的权重分别为3、2和1:
| 物品 | 权重 |
|---|---|
| 物品A | 3 |
| 物品B | 2 |
| 物品C | 1 |
我们可以使用随机数生成器来生成一个随机数,并根据权重值选择掉落的物品,例如在Java中,我们可以使用以下代码:
import java.util.Random;
public class Example {public static void main(String[] args) {Random random = new Random();// 生成一个随机整数int randomInt = random.nextInt(6);// 判断掉落的物品if (randomInt < 3) {// 掉落物品A} else if (randomInt < 5) {// 掉落物品B} else {// 掉落物品C}}
}上述代码中,我们生成一个0到5的随机整数,并根据权重值选择掉落的物品。
4.3概率分布函数
概率分布函数是一种更加复杂的概率算法。它通过一个数学函数来计算每个结果的概率值。然后,使用随机数生成器来生成一个随机数,并根据概率分布函数计算出选择的结果。 例如,我们有一个技能释放的概率分布函数,其中释放技能的概率随时间逐渐增加。我们可以使用以下的代码计算释放技能的概率,其中,time表示时间,a表示技能开始释放的时间,k表示技能释放的速率。我们可以使用随机数生成器来生成一个随机数,并使用概率分布函数计算释放技能的概率,我们可以使用以下代码:
import java.util.Random;
public class Example {public static void main(String[] args) {Random random = new Random();// 生成一个随机浮点数double randomDouble = random.nextDouble();// 计算释放技能的概率double time = getTime();double a = 0.0;double k = 1.0;double probability = 1.0 / (1.0 + Math.exp(-k * (time - a)));// 判断是否释放技能if (randomDouble < probability) {// 释放技能}}private static double getTime() {// 获取当前时间return 0.0;}
}上述代码中,我们生成一个0到1的随机浮点数,并根据概率分布函数计算释放技能的概率。如果随机数小于概率值,我们就释放技能。
五、真随机和伪随机
在游戏开发中,概率是一个非常重要的概念。我们通常使用随机数进行生成,例如怪物掉落物品、技能释放概率等等。然而,在使用随机数时,开发者需要考虑到真随机和伪随机的问题。 伪随机数生成器(PRNG)是一种算法,它可以生成一个序列的数字,这些数字看起来像是随机的,但实际上是按照算法生成的。在PRNG中,种子值是非常重要的。如果我们使用相同的种子值,我们将会获得相同的随机数序列。
真随机数生成器(TRNG)是基于物理事件的,例如大气噪声、微粒衰变等等。它们可以生成真正的随机数,因为它们是由不可预测的物理事件生成的。然而,在大多数情况下,我们可以使用伪随机数生成器来模拟真随机数。
可以说,真随机是一种自然的随机机制,用代码来实现也非常容易,只需要用一个随机数与一个常量进行比较,根据大于小于等于分别触发不同的结果就行了。例如:掷色子,掷到到的值大于3触发什么奖励,小于三又是什么奖励,等于三又是另一种奖励。而伪随机则是人为创造出来的一种机制,他需要程序员写下更多的代码,也需要数值设计者做更多的计算。例如游戏的抽奖机制,当玩家抽到第90次还没有最好品质的奖励,那么第九十次必定获得该奖励,同时在获得该道具后,概率又恢复初始;亦或者是每次没有获得该道具,概率就增加,到第90次,概率是100%,必得该奖励,同时在获得该奖励后,概率又恢复初始。
在游戏开发中,概率技术是非常重要的一部分。我们可以使用随机数生成、概率分布和随机事件触发等技术来模拟各种随机事件,使游戏更加有趣和挑战性。在实际开发中,我们应该根据具体情况选择适当的技术,并进行充分的测试和优化,以确保游戏的质量和稳定性。
相关文章:

【结构与算法】—— 游戏概率常用算法整理 | 游戏中的常见概率设计分析
📢博客主页:肩匣与橘📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢本文由肩匣与橘编写,首发于CSDN🙉📢生活依旧是美好而又温柔的,你也是✨ …...

WebRTC系列-适配GPUImage及其他视频处理改造
文章目录 1. GPUImage 的一些改动1.1 GPUImage数据输入源1.1 GPUImage数据输出源2.WebRTC摄像头采集类改造GPUImage使用OpenGL提供了很多的图像处理算法,包括最常用的美颜处理、水印等功能,这些基本的功能如何添加到WebRTC中,本文以美颜为例子,叙述主要的改造流程;同时也适…...

day43—选择题
文章目录 1.A,B两台机器都正常工作,B机器未监听任何端口.如果A机器向B机器80端口发送SYN包,会收到何种类型的回包(D)2.下列哪个IP地址可以分配给一台计算机(D)3.以下哪个ip不和10.11.12.91/28处于同一个子网(D…...

<<和>>操作符、取地址重载、const关键字
文章目录 自定义类型<<和>>重载const关键字取地址重载(类的默认构造函数) 自定义类型<<和>>重载 在内置类型中,<<和>>可以自动识别 在自定义类型冲,运算符重载,<<和>&…...

数学模型,如何计算概率?
既然是数学模型,那应该如何计算呢? 最简单的方法,当然就是用统计学的方法去计算了,简单说来,就是靠输入的上下文进行统计,计算出后续词语的概率,比如「你吃了晚饭了吗」,「你吃了」后面按照概率,名词如「饭」或「晚饭」等概率更高,而不太可能是动词,如「睡」「睡觉…...
)
【Ehcache技术专题】「入门到精通」带你一起从零基础进行分析和开发Ehcache框架的实战指南(Spring整合ehcache)
带你一起从零基础进行分析和开发Ehcache框架的实战指南(Spring整合ehcache) 回顾一下Ehcache主要的特性 Spring框架所支持的第三方缓存Spring Cache的实现方式Spring Cache基本准备工作定义Ehcache配置文件启用Spring-CacheXML风格的xml代码 JavaConfig注…...

合肥市2023年度高校毕业生“双千培养工程”培训项目学员招募公告
为贯彻落实人社部实施促进高校毕业生等青年就业创业推进计划要求,提升高校毕业生就业技能,拟开展高校毕业生“双千培养工程”培训项目。根据工作计划安排,现面向高校和社会招募学员参加培训,培训方向为大数据应用、PythonAI人工智…...
重写Properties类,实现对properties文件的有序读写,数据追加,解决中文乱码
前言 *.properties文件,是 Java 支持的一种配置文件类型,并且 Java 提供了 properties 类来读取 properties 文件中的信息。文件中以键值对 "键值"的形式,存储工程中会多次重复使用的配置信息,通过“Properties”类来读…...

态势感知与信质、信量
未来的新智能是人机环境系统智能,而人机融合的态势感知是其关键,简单地说,态势感知(situation awareness)就是智能体在“一定时间和空间环境中的元素的感知,对它们的含义的理解,并对他们稍后状态…...
与bind()重写-JS中数据类型检测汇总-装箱与拆箱-类的多种继承方案)
20230508----重返学习-call()与bind()重写-JS中数据类型检测汇总-装箱与拆箱-类的多种继承方案
day-065-sixty-five-20230508-call()与bind()重写-JS中数据类型检测汇总-装箱与拆箱-类的多种继承方案 call()与bind()重写 call()重写 call()的作用例子 let obj {name: 珠峰培训 } const fn function fn(x, y, ev) {console.log(this, x, y, ev)return x y } let res f…...
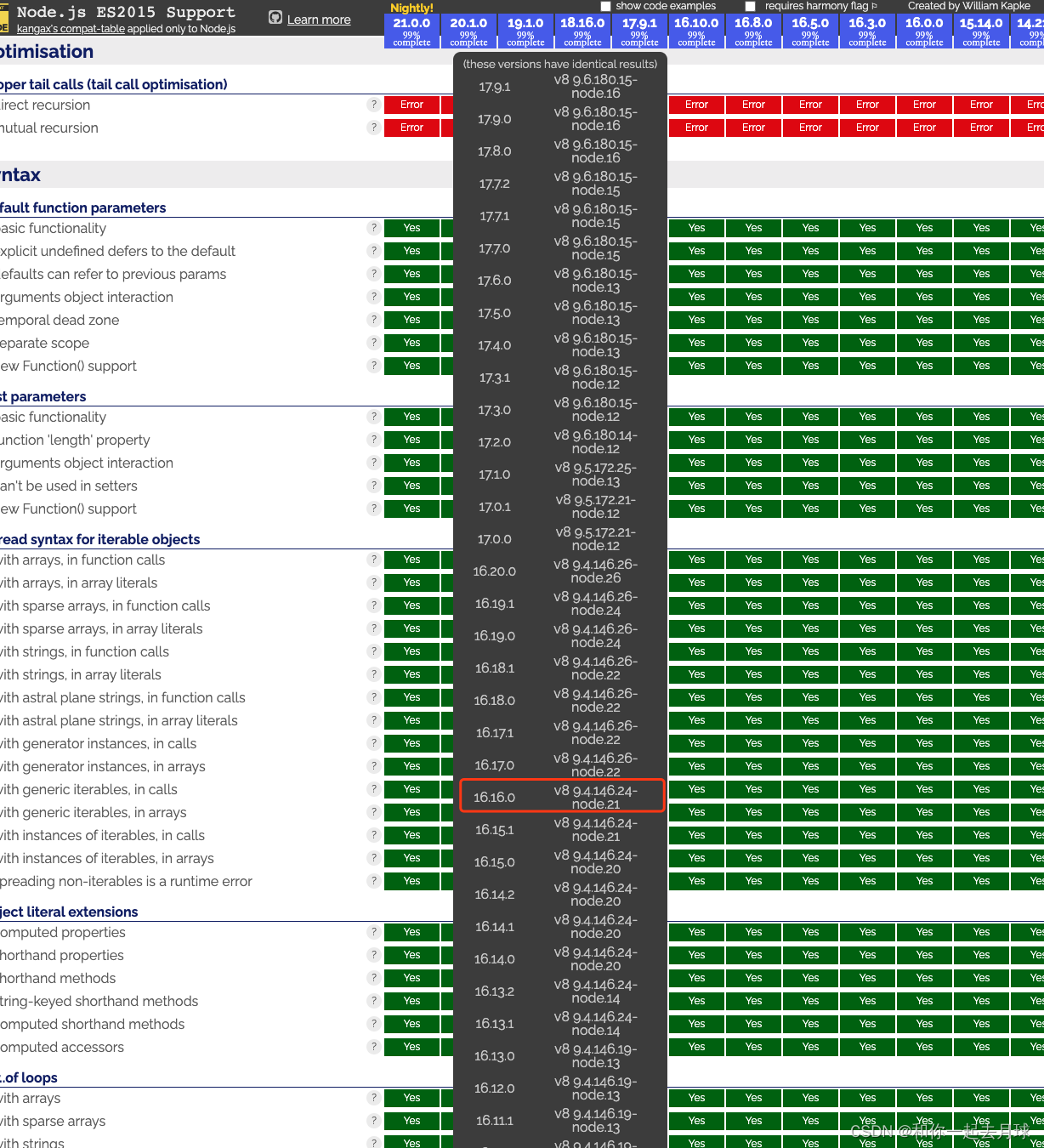
Node.js对ES6 及更高版本的支持
目录 1、简介 2、默认情况下什么特性随着 Node.js 一起发布? 3、有哪些特性在开发中? 4、移除这个标记(--harmony)吗 5、Node.js 对应 V8 引擎 1、简介 Node.js 是针对 V8 引擎构建的。通过与此引擎的最新版本保持同步&…...

【华为OD机试2023】工作安排 100% C++ Java Python
【华为OD机试2023】工作安排 100% C++ Java Python 前言 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能最优),不能保证通过率。 Tips1:机试为ACM 模式 你的代码需要处理输入输出,input/cin接收…...

面试题Spring - 关于Spring的25个经典问题和答案
文章目录 1 什么是Spring框架?Spring框架有哪些主要模块?2 使用Spring框架能带来哪些好处?3 什么是控制反转(IOC)?什么是依赖注入?4 请解释下Spring框架中的IoC?5 BeanFactory和ApplicationContext有什么区…...

C++学习day--10 条件判断、分支
1、if语句 if 语句的三种形态 形态1:如果。。。那么。。。 #include <iostream> using namespace std; int main( void ) { int salary; cout << " 你月薪多少 ?" ; cin >> salary; if (salary < 20000) { cout <&…...

和月薪5W的聊过后,才发现自己一直在打杂···
前几天和一个朋友聊面试,他说上个月同时拿到了腾讯和阿里的offer,最后选择了阿里。 我了解了下他的面试过程,就一点,不管是阿里还是腾讯的面试,这个级别的程序员,都会考察项目管理能力,并且权重…...
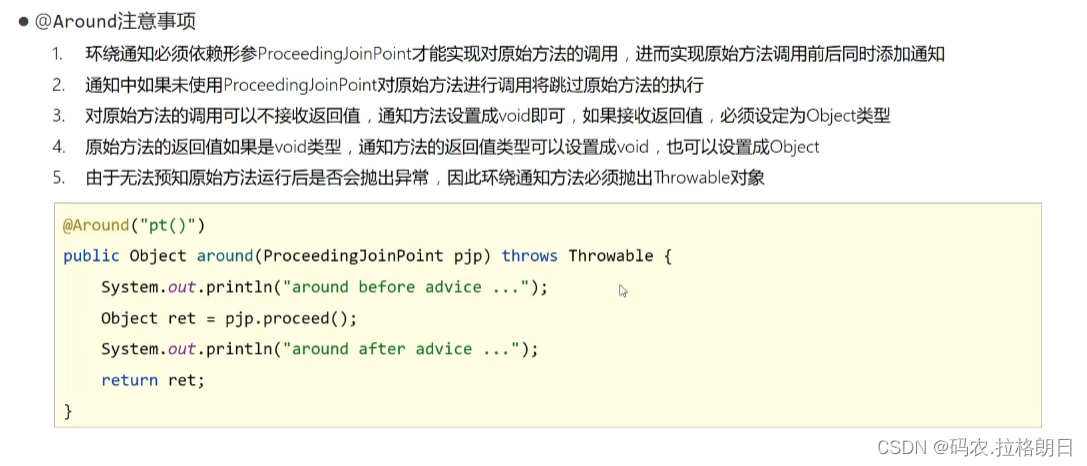
SSM框架学习-AOP通知类型
在AOP中,通知(Advice)是对切点进行操作的方法,用于实现切面定义的具体逻辑。Spring框架支持五种类型的通知: 1. 前置通知(Before advice) 在连接点执行前,执行通知 Before("**…...

微信小程序原生开发功能合集十四:登录健权及注册功能实现
本章实现微信自动登录及注册修改功能,包括匿名账号生成、权限自动检测、注册界面及注册流程的实现。 另外还提供小程序开发基础知识讲解课程,包括小程序开发基础知识、组件封装、常用接口组件使用及常用功能实现等内容,具体如下: 1. CSDN课程: https://edu.csdn…...

【Java零基础入门篇】第 ⑤ 期 - 抽象类和接口(二)
博主:命运之光 专栏:Java零基础入门 学习目标 1.了解什么是抽象类,什么是接口; 2.掌握抽象类和接口的定义方法; 3.理解接口和抽象类的使用场景; 4.掌握多态的含义和用法; 5.掌握内部类的定义方法…...
)
Halcon 集合运算(差集difference、交集intersection、并集union2、打散connection与 合集 union1)
文章目录 1 差集difference2. 交集intersection3. 并集union24 打散connection与 合集 union1 (二者互为反义词)4.1 打散connection与4.2 合集 union1 (注意与交集的区别)5 示例原图1 差集difference difference (Operator) Name difference — Calculate the difference …...

Allegro约束规则设计
首先是物理规则。 然后是间距规则。 如果有些特殊要求,还需要设计电气规则。 原则上,把规则设计好,然后把规则赋值给网络。 物理规则。PCS。 对于名字为DEFAULT的PCS,这是最基础的整板默认规则。 没有特殊要求的网络,…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
