【AI】YOLOV1原理详解
AI学习目录汇总
0、前言
YOLOv1~3作者是约瑟夫·雷德蒙(Joseph Chet Redmon),他的网站:https://pjreddie.com/
YOLOv1网站:https://pjreddie.com/darknet/yolov1/
YOLOv2网站:https://pjreddie.com/darknet/yolov2/
YOLOv3网站:https://pjreddie.com/darknet/yolo/
github:https://github.com/pjreddie/darknet
YOLOv4作者是AlexeyAB(俄),网站:https://github.com/AlexeyAB/darknet
YOLO之父Joseph Redmon因为YOLO被用于军事目的而退出,将衣钵传给了AlexeyAB
YOLOv5作者是ultralytics团队的Glenn Jocher,网站:https://github.com/ultralytics/yolov5
Glenn Jocher并没有发布YOLOv5相关论文,也不被YOLO之父Joseph Redmon认可
YOLOX作者是刘松涛
YOLOX PyTorch实现:https://github.com/Megvii-BaseDetection/YOLOX
YOLOX MegEngine实现:https://github.com/MegEngine/YOLOX
注:MegEngine是旷视深度学习框架天元
YOLOv6是由美团提出的:https://github.com/meituan/YOLOv6
YOLOv7是YOLOv4原开发团队(AlexeyAB等人)的续作,网站:https://github.com/WongKinYiu/yolov7
YOLOv8由ultralytics团队发布:
官网:https://docs.ultralytics.com/
github:https://github.com/ultralytics/ultralytics
1、简介
YOLO:You Only Look Once,一种对象检测算法,2016年由Redmon提出
优点:速度快,适合于实时检测任务;
缺点:准确度略低
2、其它算法对象检测原理
在YOLO出现之前,其它算法使用分类器对测试图像的不同切片进行评估。
例如,使用一个小窗口在图像上滑动来获取一小块图像,称为一块切片,在不同位置切出不同大小的切片后,再对这些切片进行分类处理,可以看成两个任务:找到图片中某个存在对象的区域,然后识别出该区域中具体是哪个对象。
遍历图片中所有可能的位置,地毯式搜索不同大小,不同宽高比,不同位置的每个区域,逐一检测其中是否存在某个对象,挑选其中概率最大的结果作为输出。显然这种方法效率太低。
3、YOLO原理
YOLO将图像分成NxN的格子,同时对每个格子做回归预测,输出每个格子对若干种检测目标的概率、所处的位置等信息。根据概率拼接格子就可以检测出目标的大致轮廓。
4、基本概念
4.1 神经元
神经元基本形式:y = wx + b,以下图为例:
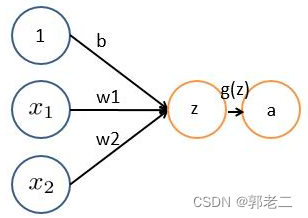
a=g(z) = g( x1 * w1 + x2 *w2 + b )
- x1、x2表示输入向量
- w1、w2为权重
- b为偏置bias
- z= x1 * w1 + x2 *w2 + b 线性组合函数
- g(z) 为激活函数
- a 为输出
4.2 激活函数
为什么要用激活函数?
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
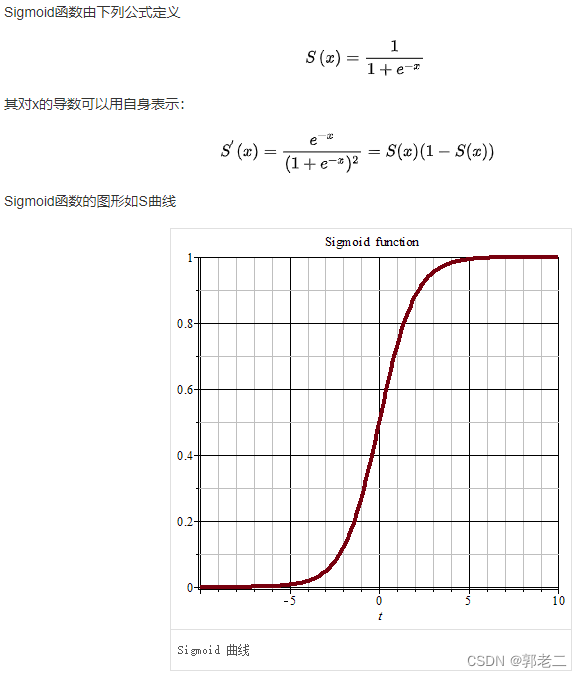
4.2.1 sigmoid
sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点:
- 优点:平滑、易于求导。
- 缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
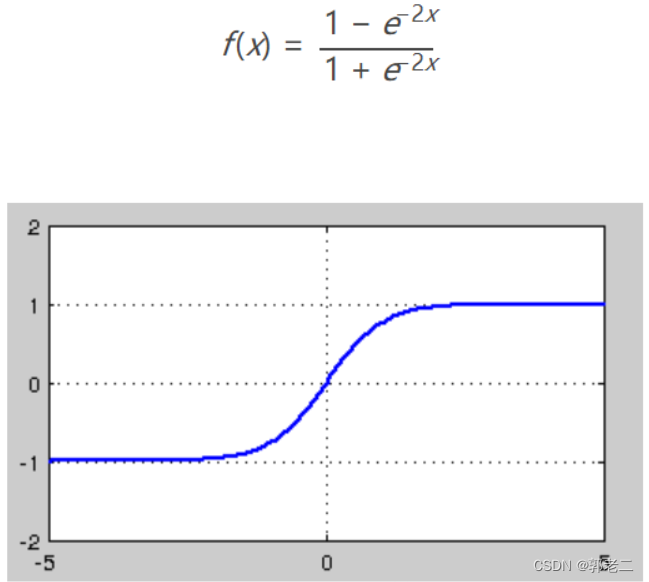
4.2.2 tanh
tanh优缺点:
- 优点:与sigmoid相比,它的输出均值是0,使得其收敛速度要比sigmoid快,减少迭代次数。
- 缺点:tanh一样具有软饱和性,从而造成梯度消失,在两边一样有趋近于0的情况
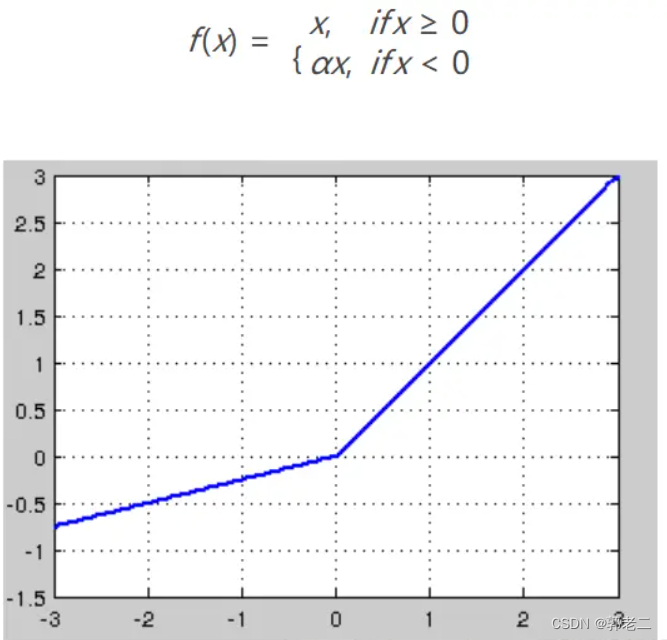
4.2.3 relu
Relu激活函数(The Rectified Linear Unit),用于隐层神经元输出。公式如下
4.3 人工神经网络(DNN)
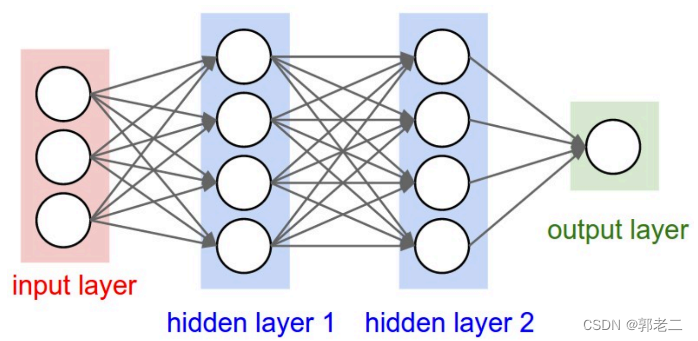
DNN层级结构如下图所示:包括1,输入层;2.隐含层(1,2,…,n);3.输出层。层级之间采用全连接(FC),激活函数一般采用sigmoid函数。优化算法一般是随机梯度下降(SGD)
4.4 卷积神经网络(CNN)
4.4.1 什么需要卷积神经网络?
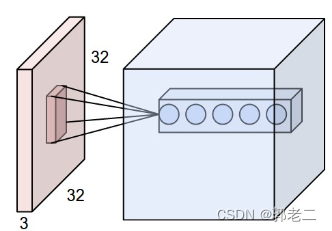
如果用普通的神经网络处理图像,一张图像的数据信息太多,输入层和隐藏层全连接时,将会产生过多的权重,例如,一张图像200x200x3(宽200,高200,颜色RGB通道数3)作为输入,和隐藏层的一个神经元将产生 2002003 = 120,000 个权重。
卷积神经网络以3个维度排列成3D体积的神经元:宽度、高度、深度;一层中的神经元只会连接到它之前的层的一小部分区域,如下图:
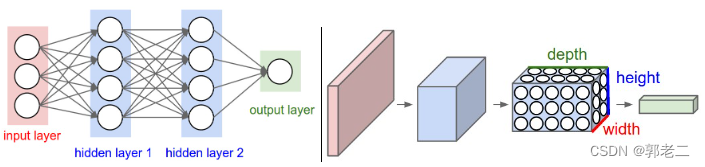
人工神经网络和卷积神经网络对比:
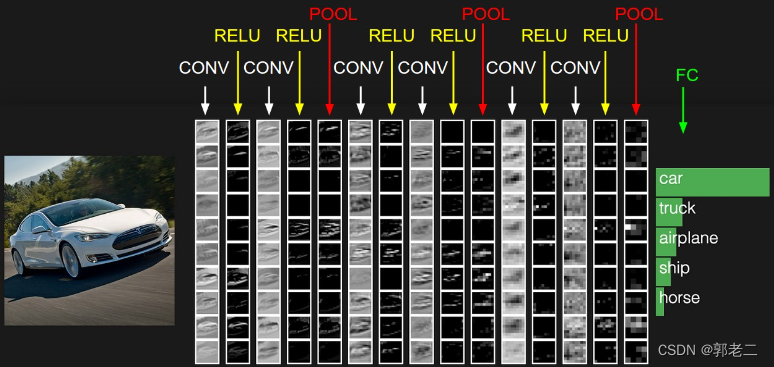
4.4.2CNN层级结构
CNN层级结构如下图所示:包括输入层,若干个(卷积层CONV+激励层(一般使用ReLU激活函数)+池化层(POOL,一般使用最大池化)),最后加一个全连接(FC),预测结果。CNN的每一层都通过可微函数将一个激活量转换为另一个激活量。
4.5 卷积层CONV
CNN笔记:通俗理解卷积神经网络
4.5.1 什么是卷积层
卷积层(Convolutional layer),卷积神经网络中每层卷积层由若干卷积单元组成,每个卷积单元的参数都是通过反向传播算法最佳化得到的。卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网路能从低级特征中迭代提取更复杂的特征。
4.5.2 超参
输入层的体积(宽、高、深度)受图像像素、色深限制为固定值,卷积层的体积大小怎么确认?
卷积层的体积受三个参数控制,称为超级参数:深度(depth)、步幅(stride)和零填充(zero-padding)
深度(depth):是指输出量的深度,将一组权重和偏置组成一个过滤器,有n个过滤器,通过卷积运算后将输出n个深度输出量
步幅(stride):滑动过滤器的步幅。当步幅为 1 时,将过滤器一次移动一个像素;当步幅为 2时,将过滤器一次移动两个像素
零填充(zero-padding):如果没有零填充,输出的体积将受输入的限制;人为将输入的数据边缘扩充为1个或多个0,可以控制输出体积的空间大小
4.5.3 卷积层体积计算
输入:W1×H1×D1
深度(过滤器):K
过滤器宽度:F
步幅:S
0填充:P
输出:W2×H2×D2
W2=(W1−F+2P)/S+1
H2=(H1−F+2P)/S+1
D2=K

4.5.4 计算输出
输出层体积中的每个点的值怎么计算?
例如:输入为X,体积为:X.shape: (11,11,4)
过滤器宽度:F = 5
步幅:S = 2
0填充:P = 0
过滤器:W0.shape: (5,5,4)
outV[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
outV[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
outV[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
outV[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
outV[0,1,0] = np.sum(X[:5,2:5,:] * W0) + b0
outV[1,1,0] = np.sum(X[2:7,2:5,:] * W0) + b0
outV[2,1,0] = np.sum(X[4:9,2:5,:] * W0) + b0
outV[3,1,0] = np.sum(X[6:11,2:5,:] * W0) + b0
……
4.6 激励层:RELU
每个卷积层后都再更一个RELU激活层
4.7 池化层:POOL
4.7.1 池化层作用
池化层夹在连续的卷积层中间, 用于减少数据和参数的个数。
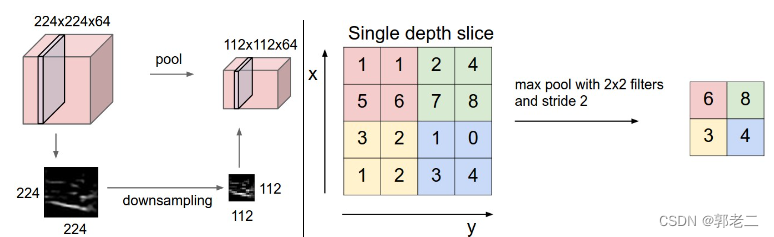
左图:大小为 [224x224x64] 的输入量经过大小为 2 、步幅为2的过滤器处理,输出量为 [112x112x64] 。请注意体积深度被保留。
右图:最常见的过滤操作是取最大值。
4.7.2 池化层体积计算
输入:W1×H1×D1
过滤器宽度:F
步幅:S
输出:W2×H2×D2
W2=(W1−F)/S+1
H2=(H1−F)/S+1
D2=D1
4.7.3 舍弃池化层
偶尔在 CONV 层中使用更大的步幅,来较少参数量,代理池化层的作用,反而训练的更好,例如变分自动编码器 (VAE) 或生成对抗网络 (GAN)。未来的架构可能会很少使用、甚至不再使用池化层。
4.8 全连接层
完全连接层中的神经元与前一层中的所有激活具有完全连接,如常规神经网络中所见。因此,它们的激活可以通过矩阵乘法和偏置偏移来计算。
4.9 过拟合
所谓过拟合(overfitting),指的是模型在训练集上表现的很好,但是在交叉验证集合测试集上表现一般,也就是说模型对未知样本的预测表现一般,泛化(generalization)能力较差。
4.10 损失函数
每一个样本经过模型后会得到一个预测值,然后得到的预测值和真实值的差值就成为损失(当然损失值越小证明模型越是成功)
最小化损失函数时,只需要使损失函数沿着负梯度前行,就能使损失函数最快下降。
梯度下降用于以最快速度、最少的步骤快速找到损失函数的极小值。
4.11 梯度下降
梯度就是导数;
梯度下降作用是找到函数的最小值所对应的自变量的值(曲线最低点对应x的值)。
梯度下降含义(具体操作)是:改变参数(权重、偏置等)的值使得导数的绝对值变小,当导数小于0时候,我们要让目前参数(权重、偏置等)值大一点点,再看它导数值。当导数大于0时候,我们要让目前参数(权重、偏置等)值减小一点点,再看它导数值。当导数接近0时候,我们就得到想要的自变量参数(权重、偏置等)了。也就是说找到这个算法最佳参数,使得拟合曲线与真实值误差最小
4.12 反向传播
参考:深度学习——反向传播(Backpropagation)
5、YOLOv1
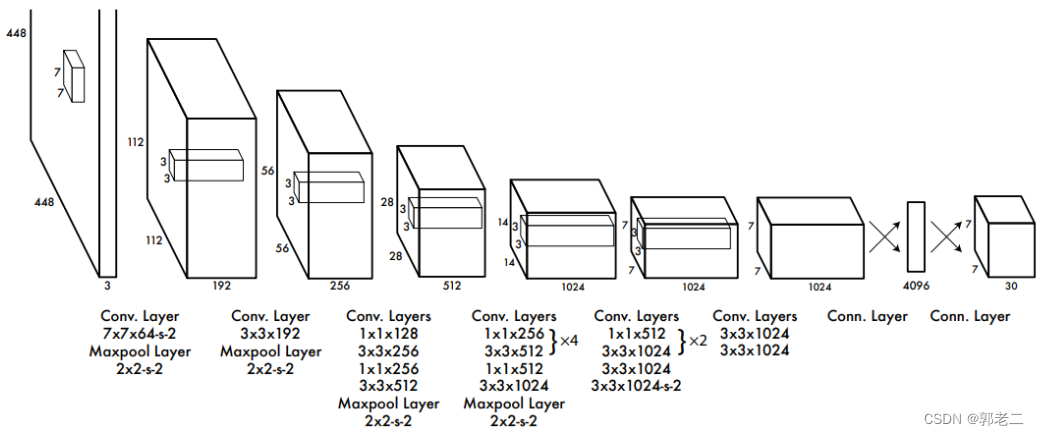
5.1 网络结构
输入层:448×448×3的彩色图片。
卷积层:由若干卷积层和最大池化层组成,用于提取图片的抽象特征。
全连接层:由两个全连接层组成,用来预测目标的位置和类别概率值。
输出层:7×7×30的预测结果。
5.2 检测原理
yolo-v1将一幅图像分成的是7x7大小的网格;
yolo-v1要求每个网格预测的是2个边界框(bounding box),每个边界框包含五个值坐标(x,y) 长宽(w,h)和置信度(confidence)
- (x,y) 表示边界框中心 相对于网格 的坐标;
- (w,h) 表示边界框 相对于整张图像 的宽和高
- 意思是边界框的中心坐标必须在网格内,但其宽和高不受网格限制、可以随意超过网格大小
- 当边界框中不存在目标时,置信度应等于0;当边界框中存在目标时,置信度应等于这一边界框和物体的真实边界框的IoU

yolo-v1默认可以预测的类别有20种,每个网格还要预测一个类别信息(C 个类)
IoU表示(真实值和预测值的交集)占(真实值和预测值的并集)的比列:

5.3 输出张量
S×S 个网格,每个网格要预测 B个边界框 ,还要预测 C 个类。输出层就是一个 S × S × (5×B+C) 的张量。对于yolo-v1,网络输出即是一个7x7x30的张量


6、YOLOV1的不足
- 每张图片能够进行分类数量太少,只有20种物体分类;
- 检测的目标的数量太少,一张图只能检测 7 * 7 = 49个目标;
- 对重叠在一起的物体检测性不好;
- YOLO对小目标的检测效果不好;
相关文章:

【AI】YOLOV1原理详解
AI学习目录汇总 0、前言 YOLOv1~3作者是约瑟夫雷德蒙(Joseph Chet Redmon),他的网站:https://pjreddie.com/ YOLOv1网站:https://pjreddie.com/darknet/yolov1/ YOLOv2网站:https://pjreddie.com/darknet…...
提高APP安全性的必备加固手段——深度解析代码混淆技术
APP 加固方式 Android APP 加固是优化 APK 安全性的一种方法,常见的加固方式有混淆代码、加壳、数据加密、动态加载等。下面介绍一下 Android APP 加固的具体实现方式。 混淆代码: 使用 ProGuard 工具可以对代码进行混淆,使得反编译出来的代…...

想让行车记录仪协助道路病害自动化检测?可以!
针对【RGB3DS道路表观病害信息智慧检测系统】,我们着重介绍过其与道路检测车做集成预装或者处理道路检测车数据的极大便利,其中之一便是可高效输出带有道路检测车桩号标记的病害报表,这是因为道路检测车数据本身具有规范性。 那么如果使用道…...
git上传大大大文件项目好折磨人
本来想把unity项目的源码上传上gitee啊,但是那个项目有1个多G,还是个半成品,要是写完,都不知道行不行 正常的上传 所用到的命令: 1、 git init 初始化,创建本地仓库 2、 git add . 添加到本地仓库 3、 git…...

java常见异常的处理方法
以下是一些常见的异常处理方法: 捕获和处理异常(try-catch): 使用try-catch语句块可以捕获并处理异常。在try块中编写可能抛出异常的代码,然后在catch块中指定异常类型,以便捕获并处理异常。 try {// 可能抛…...

上传图片到阿里云服务器base64 上传
//上传图片到阿里云服务器 function upload_Ali($remoteImage){$imageData $this->n_img_base_64($remoteImage);if ($imageData ! false) {// 初始化 cURL 句柄$ch curl_init();// 设置请求 URL 和一些 cURL 选项curl_setopt($ch, CURLOPT_URL, http://dev.com/index/aja…...

【致敬未来的攻城狮计划】— 连续打卡第二十六天:瑞萨RA Cortex-M 内核RA2E1 RT-Thread BSP 启蒙知识
系列文章目录 由于一些特殊原因: 系列文章链接:(其他系列文章,请点击链接,可以跳转到其他系列文章)或者参考我的专栏“ 瑞萨MCU ”,里面是 瑞萨RA2E1 系列文章。 24.RA2E1的 DMAC——数据传输 …...
)
2023年5月8日-5月14日(方案C,下班UE视频教程为主)
目前,ue视频教程进行到了智 慧 城 市(3.13),mysql(7.1),tf1(4.11),蓝图反射(1.9),moba(1.5)webapp(2.4),mmoarpg(00A_04),fps1_12(0:3…...

「MIAOYUN」:降本增效,赋能传统企业数字化云原生转型 | 36kr 项目精选
作为新经济综合服务平台第一品牌,36氪自2019年落地四川站以来,不断通过新锐、深度的商业报道,陪跑、支持四川的新经济产业。通过挖掘本土优质项目,36氪四川帮助企业链接更多资源,助力企业成长,促进行业发展…...

Python突破JS加密限制,进行逆向解密
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 目录标题 前言开发环境:模块使用:逆向目标逆向过程参数 JS 加密关键代码Python 登录关键代码尾语 💝 开发环境: Python 3.8 Pycharm 模块使用: time >>> 时间模块,属于内置,无…...

【Linux】exec函数族
目录 1、exec函数族的介绍2、exec相关函数 1、exec函数族的介绍 2、exec相关函数 #include <unistd.h> int execl(const char *pathname, const char *arg0, ... /* (char *)0 */ ); /* - path 需要指定的执行的文件的路径或者名称,相对路径or绝对路径- arg …...

OSQP二次规划求解库使用说明
OSQP二次规划求解库使用说明 贺志国 2023.5.10 1. 凸二次规划的一般表达式 m i n 1 2 x T P x q T x s . t . l ≤ A x ≤ u min \quad \frac{1}{2}x^T Px q^Tx \qquad s.t. \quad l \leq Ax \leq u min21xTPxqTxs.t.l≤Ax≤u 其中, P P P称为内核矩阵&#x…...

Elasticsearch(一)
Elasticsearch(一) 初始elasticsearch 什么是elasticsearch elasticsearch是一款非常强大的开源搜索引擎,可以帮助我们从海量数据中快速查找到需要的内容 elasticsearch结合kibana、Logstash、Beats,也就是elastic stack&…...

深入探究Java中的枚举类型:定义、特性和应用
引言: 在Java编程中,枚举类型是一种强大而灵活的工具,用于定义一组具名的常量。它不仅提供了代码可读性和可维护性的优势,还为开发人员提供了一种更安全和结构化的方式来处理固定的常量集合。本文将深入探讨Java中的枚举类型&…...

linux密码忘了?一招解决
目录 一、前言 二、进入编辑界面 三、单用户模式 四、修改密码 五、更新信息 六、退出 七、验证 一、前言 版本:centos7.9、VMware15.5 在我们学习linux运行级别的时候,面试题可能会出如何找回root密码,下面来详细的介绍一波ÿ…...
苹果mac清理软件CleanMyMac X v4.13兼容13系统,堪称Mac最好的系统清理工具
CleanMyMac X for mac是MacOS上一款Mac清理优化工具,不仅包含各种清理功能,更是具有卸载器、维护、扩展、碎纸机这些实用功能,可以同时代替很多工具。它可以清理,优化,保养和监测您的电脑,确保您的Mac运行…...
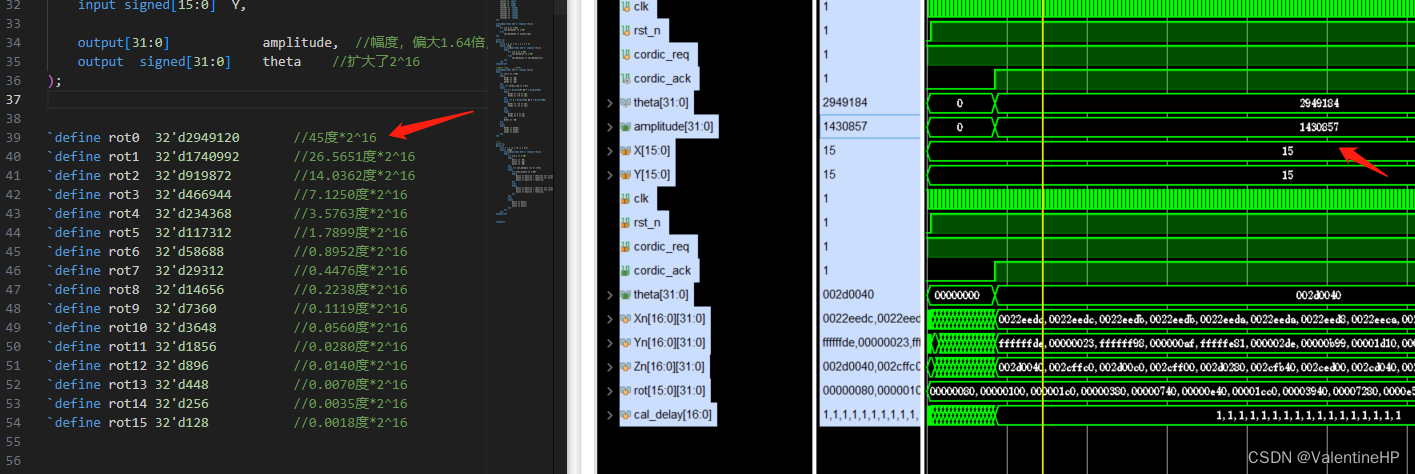
FPGA实现Cordic算法求解arctan和sqr(x*2 + y* 2)
一. 简介 由于在项目中需要使用的MPU6050,进行姿态解算,计算中设计到**arctan 和 sqr(x2 y 2),**这两部分的计算,在了解了一番之后,发现Cordic算法可以很方便的一次性求出这两个这两部分的计算。另外也可以一次性求出sin和cos的…...

【最终截稿 | Springer 独立出版 | EI稳定检索】 2023年绿色建筑国际会议(ICoGB 2023)
会议简介 Brief Introduction 2023年绿色建筑国际会议(ICoGB 2023) 会议时间:2023年5月21日-23日 召开地点:瑞典斯德哥尔摩 大会官网:www.icogb.org ICoGB 2023将围绕“绿色建筑”的最新研究领域而展开,为研究人员、工程师、专家学…...

Flutter常用状态管理框架及优缺点
Flutter 中常见的状态管理框架有以下几种: Provider: Provider 是一个轻量级的状态管理框架,可用于单个 Widget 或整个 Widget 树中分发状态。它通过 InheritedWidget 和 ChangeNotifier 来实现状态管理,并支持依赖项注入。Redux…...
Ubuntu 20.04 系统配置 OpenVINO 2022.3 环境
由于 OpenVINO 2021 版本在调用 IECore 时会出现 Segmentation fault 的问题,因此需要将其升级为 2022 版本的。 1. 卸载原来版本的 OpenVINO 进入OpenVINO的卸载目录,通常在 /opt/intel 文件夹下, cd /opt/intel/openvino_2021/openvino_…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
