MATLAB连续LTI系统的时域分析(十)
目录
1、实验目的:
2、实验内容:
1、实验目的:
1)掌握利用MATLAB对系统进行时域分析的方法;
2)掌握连续时间系统零输入响应的求解方法;
3)掌握连续时间系统零状态响应、冲激响应和阶跃响应的求解方法;
4)掌握利用计算机进行卷积积分和卷积和计算的方法。
2、实验内容:
2-1)、已知某系统可以由如下微分方程描述y′′(t)+ y′(t)+6y(t)=x(t),利用MATLAB绘出该系统冲激响应和阶跃响应的时域波形。(注:题中时域范围可取[0 10],参考函数tf、impulse、step)
a = [1 1 6]; b = [1]; %微分方程左右两端多项式的系数矩阵
time = 0:0.01:10; %时域范围[0 10]
sys = tf(b,a);
y1 = impulse(sys,time); %系统的冲激响应
y2 = step(sys,time); %系统的阶跃响应
subplot(1,2,1), plot(time,y1), xlabel('时间t'), title('冲激响应');
subplot(1,2,2), plot(time,y2), xlabel('时间t'), title('阶跃响应');2-2)、编程实现如下图所示的两个波形的卷积,并绘制出卷积后的波形。(要求:先构建两信号卷积函数,而后通过调用该函数实现做题)
编写的卷积函数
function [t,x] = sss_conv(x1,x2,t1,t2,dt)
%文件名与函数名对应
%自写的卷积函数
x = conv(x1,x2)*dt;
t0 = t1(1) + t2(1);
L = length(x1) + length(x2)-2;
t = t0:dt:(t0+L*dt);
end功能实现
dt = 0.01;
x1 = -1 : dt : 1;
f1t = 2*(heaviside(x1+1) - heaviside(x1-1));
% plot(x1,f1t);
x2 = -2 : dt : 2;
f2t = heaviside(x2+2) - heaviside(x2-2);
% plot(x2,f2t);
[t, f] = My_conv(f1t, f2t, x1, x2, dt); %调用卷积函数
plot(t, f);
axis([-4 4 -1 5]);2-3)、已知系统的微分方程为:,x(t)为e-tu(t),用数值法求零状态响应y(t)并绘图。(注:题中时域范围可取[0 10])
a = [1 4 4]; b = [1 3]; dt = 0.1; t = 0:dt:10; % 微分方程左侧系数向量a,微分方程右侧系数向量b
[r,p] = residue(b,a); % 用residue函数(参见12.1.2节)求出其特征根p1、p2和相应的留数r1、r2h = r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t); %叠加各根分量
subplot(1,2,1), plot(t,h), title('冲激响应');
x = exp(-t); % t已经大于0了
y = conv(x,h)*dt; % 求x和h的卷积,长度为2*length(t)-1
subplot(1,2,2), plot(t,y(1:length(t))), title('零状态响应');2-4)、分别用数值法和符号法求齐次微分方程在给定初始条件下的零输入响应波形,y′′(t)+2y(t)=0,y(0_)=3,y′(0_)=4。(注:题中时域范围可取[0 10],以实现方法作为图形标题名称)
% (1)数值法
a = [1 0 2]; % 方程左端系数向量
n=length(a)-1; % 微分方程的阶数(即根的数量)
Y0 = [3 4]; % 初始条件向量
p=roots(a); % 求特征方程的根
V=rot90(vander(p)); % 生成范德蒙特矩阵
C= V\Y0'; % 求对应于各特征根的系数 左除
dt = 0.1; tf = 10; % 时域取值范围[0 10]
t = 0:dt:tf; % 时域取值范围[0 10]
y = zeros(1,length(t));
for k=1:n y = y + C(k)*exp(p(k)*t); end % 将各分量叠加,得到零输入响应的通式
subplot(121);
plot(t, y), xlabel('t'), ylabel('real(y)'); %零输入响应的实部随时间变化的趋势
title('数值法');% 符号法
eq='D2y+2*y=0'; con='y(0)=3, Dy(0)=4';
y = dsolve(eq, con); y=simplify(y);
subplot(122);
ezplot(y, t); %一定要加参数t,限制时间的范围,保证波形正确
axis([0 10 -5 5]); % 限制xy轴范围
title('符号法'); 2-5)、求系统,y′(0+)=-1;y(0+)=0的全响应。(注:题中时域范围可取[0 10],参考函数tf2ss、lsim)
clear
b = [1]; a = [1 0 1];
t = 0:0.1:10; x = cos(t);
sys1 = tf(b,a); %系统函数模型
y1 = lsim(sys1,x,t); %零状态响应
% subplot(1,2,1),plot(t,y1);
xlabel('时间');title('零状态响应');
[A B C D] = tf2ss(b,a); %系统函数模型转化成状态空间模型参数
sys2 = ss(A,B,C,D) ;zi = [-1 0]; %产生状态空间模型和初始状态矩阵
y2 = lsim(sys2,x,t,zi); %全响应
% subplot(1,2,2);
plot(t,y2);
xlabel('时间t');title('全响应');
相关文章:

MATLAB连续LTI系统的时域分析(十)
目录 1、实验目的: 2、实验内容: 1、实验目的: 1)掌握利用MATLAB对系统进行时域分析的方法; 2)掌握连续时间系统零输入响应的求解方法; 3)掌握连续时间系统零状态响应、冲激响应和…...
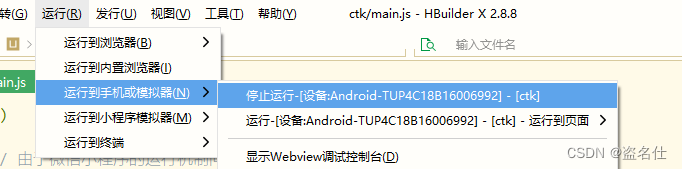
HBuilderX使用
HBuilderX使用(Vue前后端分离) 概述:DCloud开发者后台 DAccount Service 1、官网下载开发工具:HBuilderX-高效极客技巧 注意:安装目录路径中不能出现中文特殊字符,否则会造成项目无法编译。比如C:/Progr…...
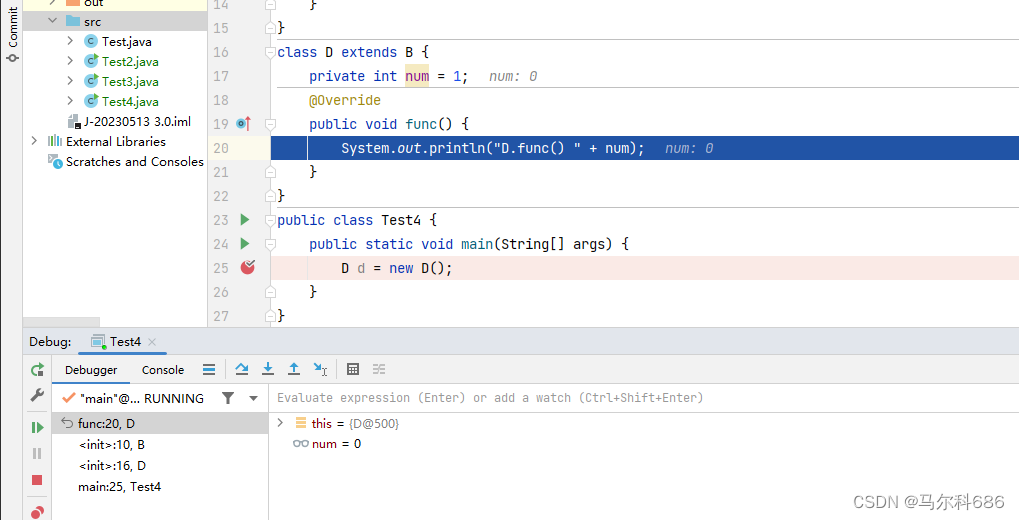
【JavaSE】多态(多态实现的条件 重写 向上转移和向下转型 向上转型 向下转型 多态的优缺点 避免在构造方法种调用重写的方法)
文章目录 多态多态实现的条件重写向上转移和向下转型向上转型向下转型 多态的优缺点避免在构造方法种调用重写的方法 多态 一种事物,多种形态。 多态的概念:去完成某个行为,当不同对象去完成时会产生出不同的状态。 多态实现的条件 1.必须…...
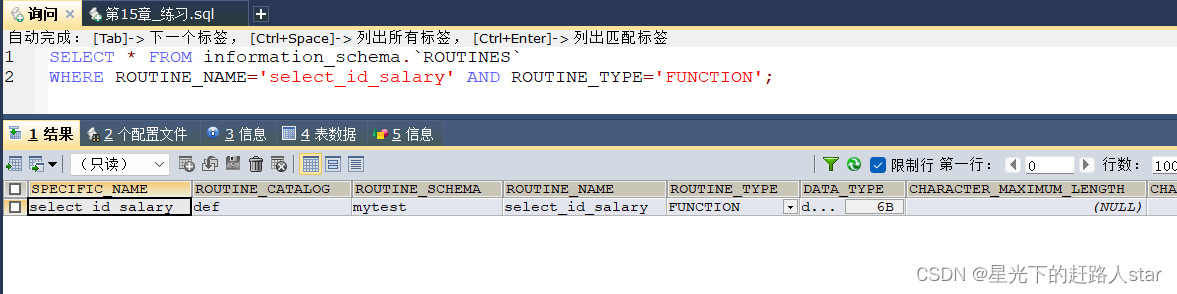
MySQL学习---13、存储过程与存储函数
1、存储过程概述 MySQL从5.0版本开始支持存储过程和函数。存储过程和函数能够将负杂的SQL逻辑封装在一起,应用程序无序关注存储过程和函数内部复杂的SQL逻辑,而只需要简单的调用存储过程和函数就可以。 1.1 理解 含义:存储过程的英文是Sto…...

Mysql日志管理、备份与恢复
文章目录 一、Mysql日志管理1.mysql日志2.日志种类3.日志的查询4.配置日志文件 二、Mysql备份与分类1.数据备份的重要性 一、Mysql日志管理 1.mysql日志 Mysql的日志默认保存位置为/usr/local/mysql/date,Mysql的日志配置文件为/etc/my.cnf,里面有一个…...

STM32单片机声控语音识别RGB彩灯多种模式亮度可调WS2812彩灯
实践制作DIY- GC0129-语音识别RGB彩灯 一、功能说明: 基于STM32单片机设计-语音识别RGB彩灯 二、功能介绍: STM32F103C系列最小系统板5VUSB电源64个灯珠的WS2812灯板1个开关键(3档亮度调节)1个模式切换键(白灯 红灯…...

高校9大学术工具推荐,一定要用起来哦!
1、文献管理工具:例如EndNote、Mendeley和Zotero,这些工具可以帮助您整理、管理和引用文献。 2、数据分析工具:例如SPSS、R和Python等,用于进行统计分析和数据处理。 3、学术写作工具:例如LaTeX和Microsoft Word&…...

记一次压力测试
性能测试文档 背景 为对产品性能有一定了解,现将产品展开一次性能测试; 环境与工具 本章为基本工具准备及linux命令说明,无先后顺序。 Xshell工具 本文使用Xshell在Windows界面下远程登录linux主机安装Xshell直接全部选择默认选项即可&…...

一个文明是否有竞争力,在很大程度上取决于信息传递的效率。
文章目录 引言I 有效地传递信息1.1 信息传播分类1.2 信息传递的有效性II 科技进步的必要条件和充分条件2.1 能量总量2.2 能量密度2.3 衡量科技成就的大小2.4 科学的诞生的意义:获得叠加式收益引言 科技进步的必要条件是能量总量,而充分条件是能量密度。一个文明是否有竞争力,…...

测试4年,跳槽一次涨8k,我跳了3次···
最近有人说,现在测试岗位初始工资太低了,有些刚刚入行的程序员朋友说自己工资连5位数都没有.....干了好几年也没怎么涨。看看别人动辄月薪2-3万,其实我想说也没那么难。说下如何高效地拿到3w。 1.暂且把刚入行的条件设低些吧,大专…...
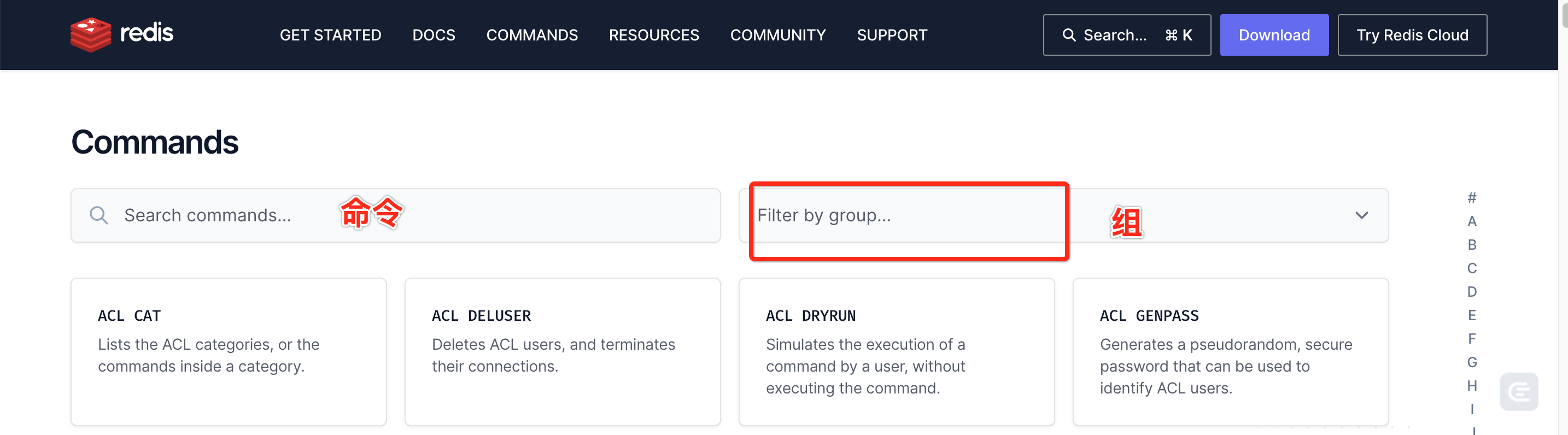
Redis 入门教程(简单全面版)
1 安装: 1.1 生产环境安装 注意: 1、如果安装过程有问题可以参考源代码中的 README.md 文件 2、如果服务器只安装一个 redis 通常选择 /usr/local/redis 作为安装目录,如果安装多台则建议带上 服务名称 区分(建议带上 服务名称 区…...

java并发-AQS
当我们使用Java并发编程时,我们经常会听到“AQS”的概念。AQS代表“AbstractQueuedSynchronizer”,是Java并发包中的一个重要组件。AQS提供了一个框架,使得开发者可以轻松地实现各种同步器,例如锁,信号量,倒…...

openAI图像生成开发文档
图像生成 了解如何使用我们的 DALLE 型号 介绍 图像 API 提供了三种与图像交互的方法: 根据文本提示从头开始创建图像根据新的文本提示创建现有图像的编辑创建现有图像的变体 本指南介绍了使用这三个 API 终结点的基础知识以及有用的代码示例。要了解它们的实际…...

Python综合案例—利用tkinter实现计算器的程序
目录 一、导入 tkinter 库 定义全局变量 二、定义回调函数 三、创建窗口对象 四、创建标签控件 五、创建数字按钮 六、创建加、减、乘、除和等于按钮 七、创建清空按钮 八、总结 用Python实现计算器可以让我们更好地理解面向对象编程、GUI 编程和事件驱动编程等概念&a…...
canvas学习笔记
其实还有react还没有学,但是公司技术栈里面有canvas,所以先系统学习一下canvas 一、canvas 简介 <canvas> 是 HTML5 新增的,一个可以使用脚本(通常为 JavaScript) 在其中绘制图像的 HTML 元素。它可以用来制作照片集或者制作简单(也…...
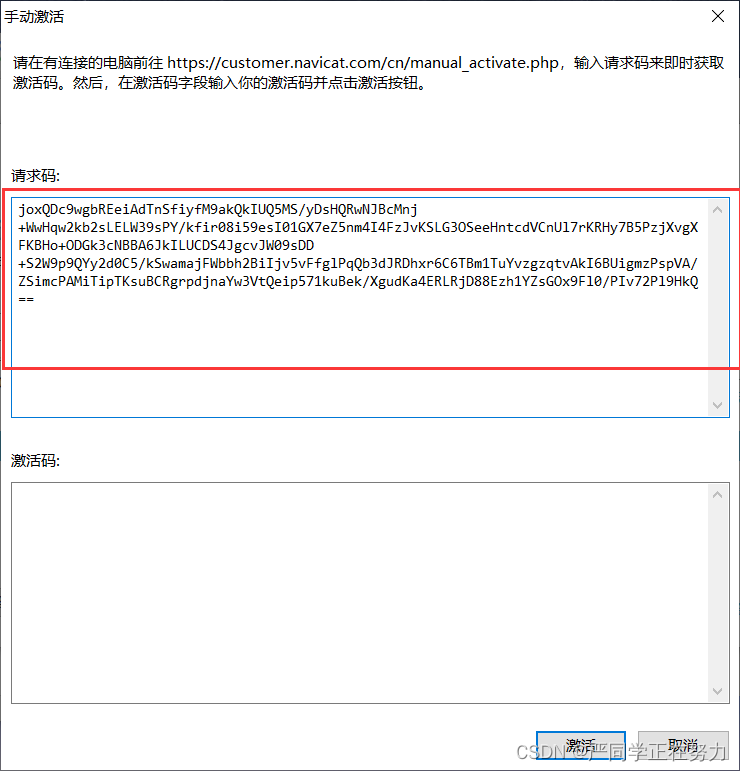
Navicat Premium 15安装注教程
Navicat Premium 15安装 准备工作 下载好安装包navicat150_premium_cs_x64和安装完成Navicat Premium 15 链接:https://pan.baidu.com/s/1TJs3pjAXJXhu7-13DJLzpg 提取码:hunk 安装Navicat Premium 15 无脑操作,下一步下一步就行了&…...
yolo v8
这个系列代码被封装的非常的精致,对二次开发不太友好,虽然也还是可以做些调节 模型的导出 有三种方式试过,都可以导出onnx的模型 1. 用yolov8 源码来自:ultralytics\yolo\engine\exporter.py (不固定尺寸) yolo export modelpa…...
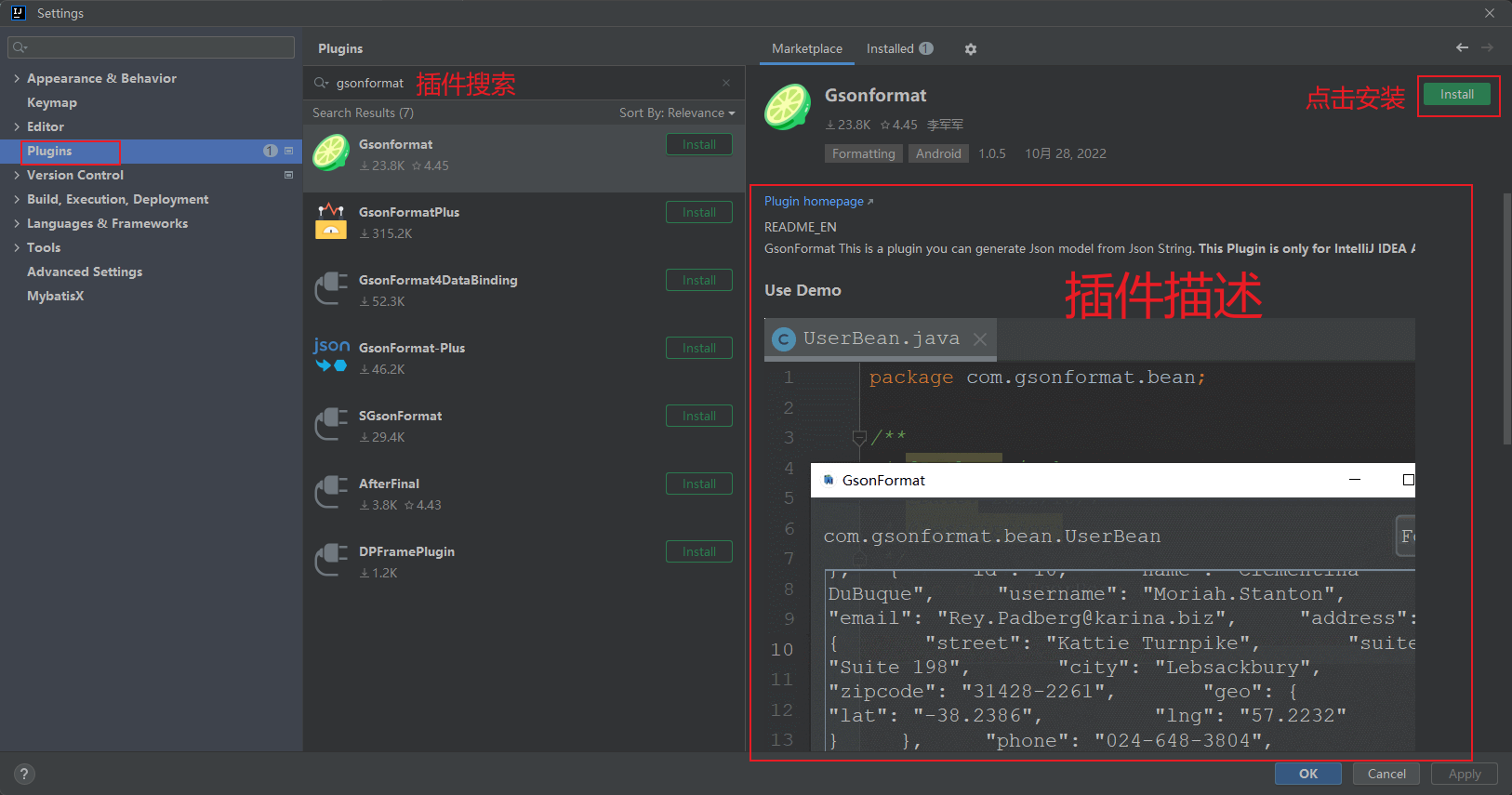
2022IDEA的下载、安装、配置与使用
文章目录 1.IntelliJ IDEA 介绍1.2 JetBrains 公司介绍1.2 IntelliJ IDEA 介绍1.3 IDEA 的主要功能介绍1.3.1 语言支持上1.3.2 其他支持 1.4 IDEA 的主要优势:(相较于 Eclipse 而言)1.5 IDEA 的下载地址1.6 官网提供的详细使用文档 2.windows 下安装过程2.1 安装前的…...
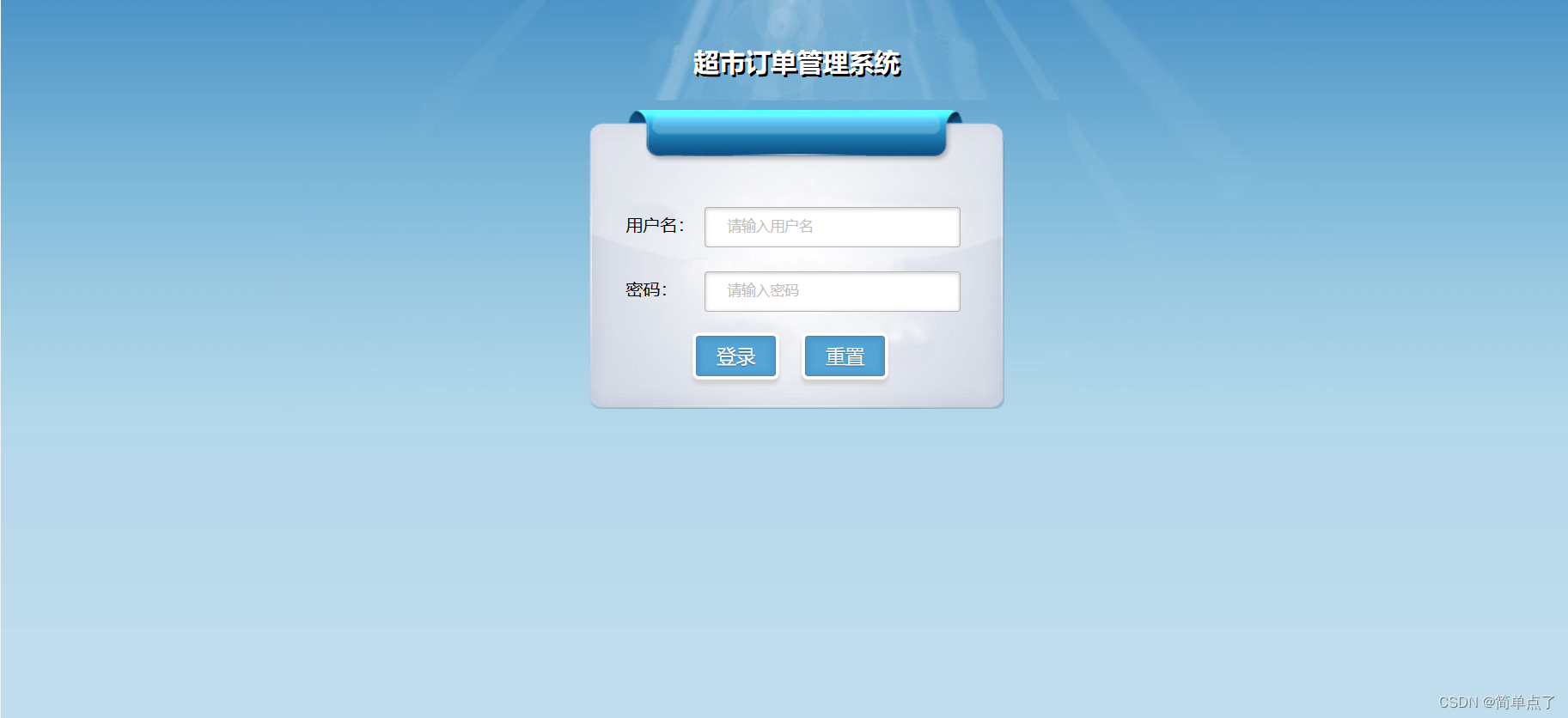
实验十 超市订单管理系统综合实验
实验十 超市订单管理系统综合实验 应粉丝要求,本博主帮助实现基本效果! 未避免产生版权问题,本项目博主不公开源码,如果您遇到相关问题可私聊博主! 一、实验目的及任务 通过该实验,掌握利用SSM框架进行系…...
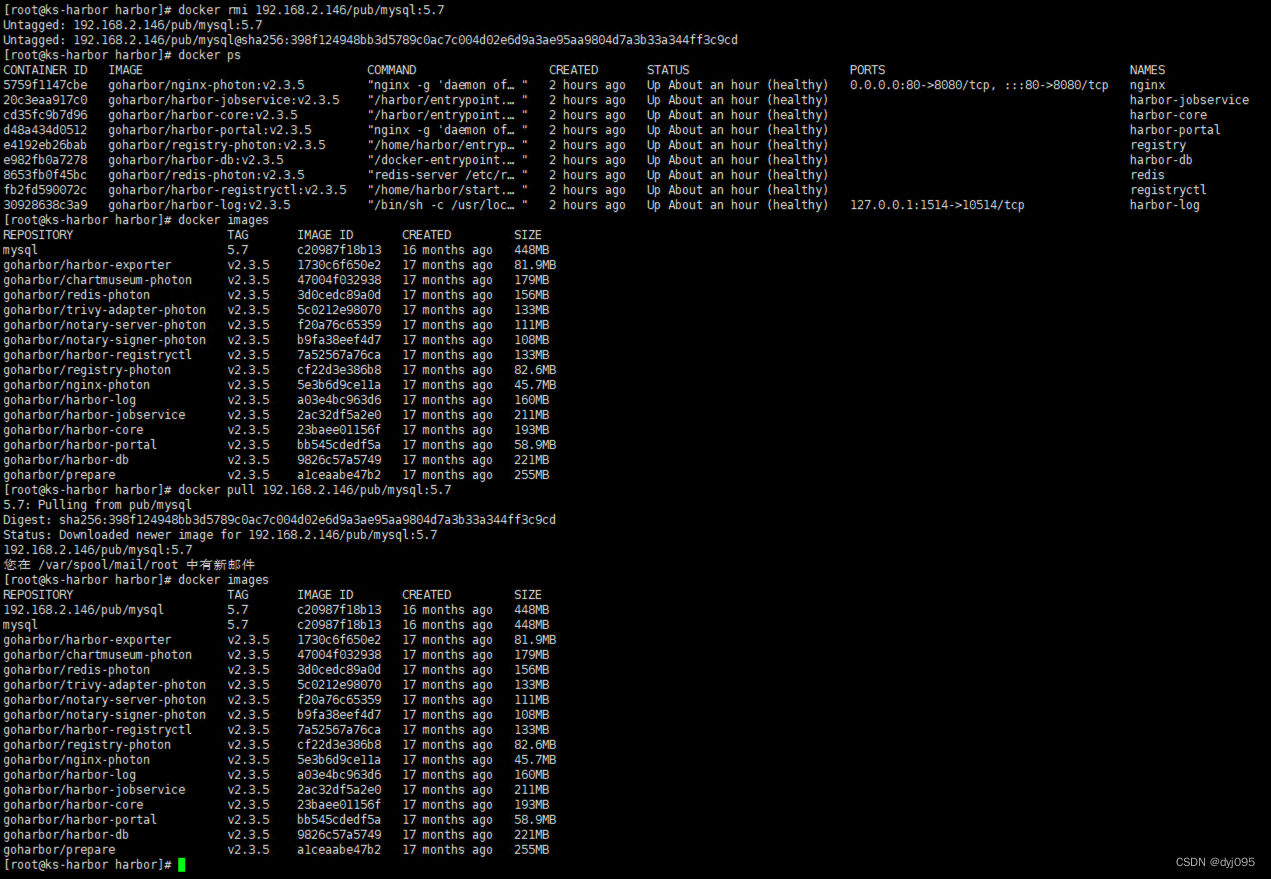
微服架构基础设施环境平台搭建 -(二)Docker私有仓库Harbor服务搭建
微服架构基础设施环境平台搭建 -(二)Docker私有仓库Harbor服务搭建 通过采用微服相关架构构建一套以KubernetesDocker为自动化运维基础平台,以微服务为服务中心,在此基础之上构建业务中台,并通过Jekins自动构建、编译、…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...



