牛客小白月赛 D.遗迹探险 - DP
题目描述
小Z是一名探险家。有一天,小Z误入了一个魔法遗迹。以下是该遗迹的具体组成:
1. 在 x 轴和 y 轴构成的平面上,满足在 1≤x≤n,1≤y≤m 的区域中(坐标(x,y)表示平面上的第x行的第y列),每个整数坐标 (x,y) 都有一个宝藏,坐标为(i,j)的宝藏的价值为ai,j(请注意,宝藏的价值可以为负)。换句话说,这个区域上的整点都有一个宝藏。
2. 对于任意一对点 (x1,y1) 和 (x2,y2),如果它们的横坐标相等,纵坐标之差为 1,则纵坐标小的点有一条道路可以到达纵坐标大的点,或者它们的纵坐标相等,横坐标之差为 1,则横坐标小的点有一条道路可以到达横坐标大的点。换句话说,(x,y)可以到达(x+1,y)或(x,y+1),反之不然。
3. 遗迹的入口在(1,1),出口在(n,m),小Z从入口进入后从出口离开,在移动的过程中他会将他所遇到的所有宝藏全部收集起来。
小Z想知道从进入到离开遗迹,他在离开遗迹时所能获得的宝藏的价值的和最大为多少。
作为一个有智慧的探险家,小Z当然会解决这个问题。但是由于这个遗迹具有魔法,问题就变得不是那么简单了。
在小Z进入该遗迹前,遗迹的魔法发动,它会在若干个具有宝藏的位置生成一个传送门。若小Z所在的坐标有传送门,则他可以通过这个传送门到达其它任意一个具有传送门的位置(当然,他也可以选择不使用传送门),并且小Z在使用一次传送门后,所有的传送门都会消失。换句话说,小Z只能最多使用一次传送门。
该遗迹具有魔法,每当小Z离开某个整点,该整点就会重新生成一个价值为ai,ja_{i,j}ai,j的宝藏。
小Z会进入TTT次该遗迹。请你帮助小Z计算出,对于每次进入遗迹,在给定传送门的坐标的情况下,他在离开遗迹时所能获得的宝藏的价值的和最大为多少?
输入描述:
第一行包含两个正整数 n,m (2≤n≤103),变量的含义如题意所示。接下来有n行,每行有m个整数,其中第i行第j列的数字代表坐标(i,j)的宝藏的价值ai,j (∣ai,j∣≤109)。接下来有一个数字T (1≤T≤103),表示小Z进入的遗迹次数。对于每次进入遗迹,第一行将给出一个整数k (2≤k≤5),表示传送门的个数。接下来k行,每行有两个整数x,y (1≤x≤n,1≤y≤m),表示坐标(x,y)上有一个传送门。 数据保证传送门的坐标两两不同。
输出描述:
输出T行,第i行表示第i次进入该遗迹的宝藏的最大值。
示例1
输入
3 3 1 2 3 4 5 6 7 8 9 2 2 1 1 3 3 3 1 1 1 3 3 1输出
58 41
分析:
计算两次dp,第一次计算从(1,1)到(i,j)的最大价值,第二次计算从(n,m)到(i,j)的最大价值(即任何一个点到(n,m)的最大价值),可以发现进入传送门可以多走一段路,那么最大价值就是不用传送门走到(n,m)的最大价值f(n,m),走到传送门的价值加上传送后(i,j)到(n,m)的最大值f(i1,j1)+g(i2,j2)。l另外需要预处理,注意存在负数情况。
代码:
#include <bits/stdc++.h>using namespace std;typedef pair<int,int> pii;
typedef long long ll;const int N=1010;ll a[N][N];
ll f[N][N];
ll g[N][N];int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,m;cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}memset(f,-0x3f,sizeof f);memset(g,-0x3f,sizeof g);f[0][1]=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];}}g[n][m+1]=0;for(int i=n;i>=1;i--){for(int j=m;j>=1;j--){g[i][j]=max(g[i+1][j],g[i][j+1])+a[i][j];}}int t;cin>>t;while(t--){vector<pii> d;int k;cin>>k;while(k--){int x,y;cin>>x>>y;d.push_back({x,y});}ll ans=f[n][m];for(int i=0;i<(int)d.size();i++){for(int j=0;j<(int)d.size();j++){if(i==j) continue;int x1=d[i].first;int x2=d[j].first;int y1=d[i].second;int y2=d[j].second;ans=max(ans,f[x1][y1]+g[x2][y2]);}}cout<<ans<<'\n';}
}相关文章:

牛客小白月赛 D.遗迹探险 - DP
题目描述 小Z是一名探险家。有一天,小Z误入了一个魔法遗迹。以下是该遗迹的具体组成: 1. 在 x 轴和 y 轴构成的平面上,满足在 1≤x≤n,1≤y≤m 的区域中(坐标(x,y)表示平面上的第x行的第y列),每个整数坐标 (x,y) 都有…...

前端架构师-week6-require源码解析
require 源码解析——彻底搞懂 npm 模块加载原理 require 的使用场景 加载模块类型 加载内置模块:require(fs)加载 node_modules 模块:require(ejs)加载本地模块:require(./utils)支持文件类型 加载 .js 文件加载 .mjs 文件加载 .json 文件…...

作为 IT 行业的过来人,你有什么话想对后辈说的?
作为 IT 行业的过来人,我想对后辈们说,要不断学习和探索新技术,但同时也要注意保持专注和耐心。在这个快速变化的时代,技术更新换代太快,可能会让人感到焦虑和无助,但只要有耐心并专注于自己所做的事情&…...
)
表数据编辑(数据库)
目录 一、插入数据 1.插入单个元组: INSERT…VALUES语句 2.插入子查询的结果: INSERT…SELECT语句 3.使用SELECT…INTO语句进行数据插入 二、修改数据 1、数据修改语句:UPDATE 2、修改给定表的所有行 3、基于给定表修改某…...
考虑多能负荷不确定性的区域综合能源系统鲁棒规划(Python代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
RocketMQ整理
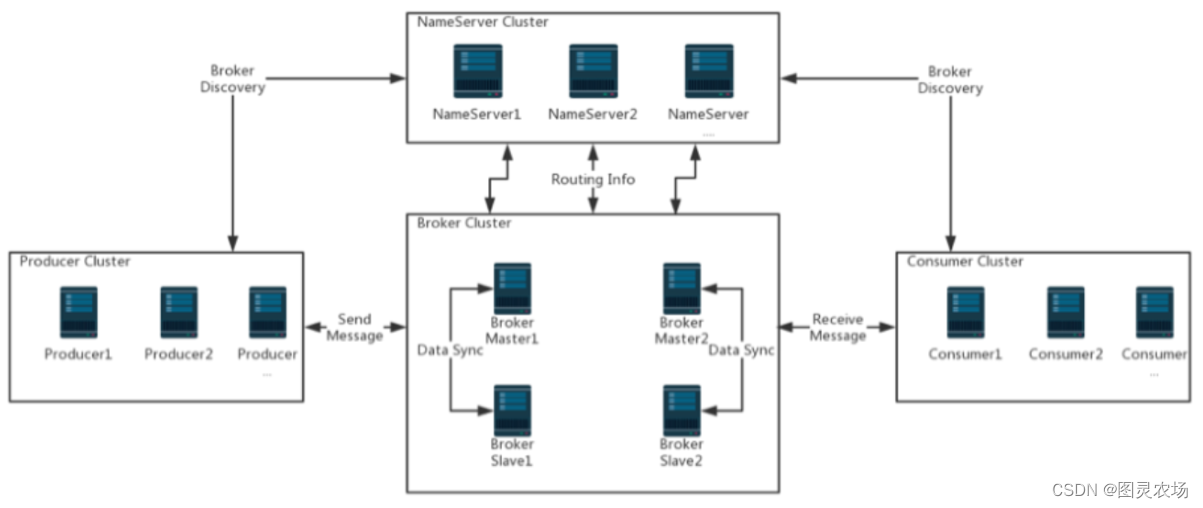
RocketMQ在阿里云上的商业版本,集成了阿里内部一些更深层次的功能及运维定制。开源版本,功能上略有缺失,但大体上是一样的。 使用Java开发,便于深度定制。最早叫MetaQ。消息吞吐量虽然依然不如Kafka,但是却比RabbitMQ高很多。在阿里内部,RocketMQ集群每天处理的请求数超过…...

Springboot +Flowable,会签、或签简单使用(二)
一.简介 **会签:**在一个流程中的某一个 Task 上,这个 Task 需要多个用户审批,当多个用户全部审批通过,或者多个用户中的某几个用户审批通过,就算通过。 例如:之前的请假流程,假设这个请假流程…...
将核心交换机配置为NTP服务器
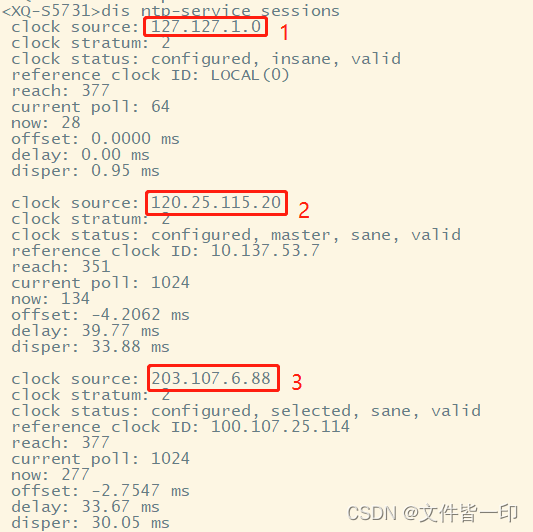
AR配置外源NTP 1.配置ntp <XQ-R1220>sys [XQ-R1220]ntp-service unicast-server 120.25.115.20 #阿里云ntp [XQ-R1220]ntp-service unicast-server 203.107.6.88 #阿里云ntp 2.查看ntp状态 <XQ-R1220>display ntp status clock sta…...

application.properties文件注释
这是一个常用的Spring Boot配置文件 在这里,我们可以配置应用程序的各种属性 服务器端口号 server.port8080 数据库配置 spring.datasource.urljdbc:mysql://localhost:3306/test spring.datasource.usernameroot spring.datasource.password123456 spring.datasou…...

MySql查询报错this is incompatible with sql_mode=only_full_group_by
错误示例 Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column ‘yiliaohaocai_new.a.id’ which is not functionally dependent on columns in GROUP BY clause; this is incompatible with sql_modeonly_full_group_by 原因 SQL …...
VMware Workstation 网络备忘 + 集群规模
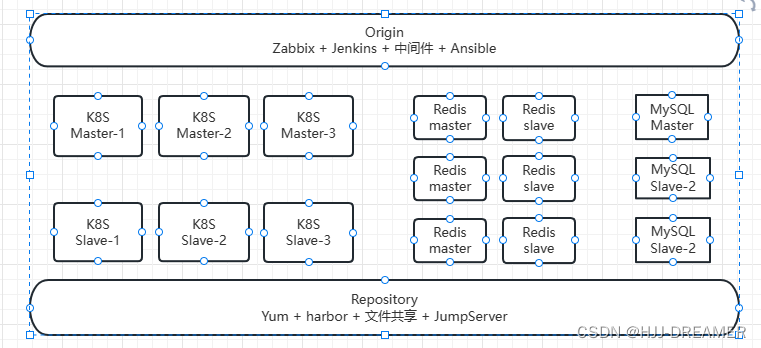
概述 在虚拟机中部署服务,进行IP规划,进行相关的前期准备 3 张网卡 2个不同的网段 1个NAT 概述截图 NAT 截图 VMnet0 截图 VMnet1 截图 总结: 网卡(网络适配器)名称IP网段备注NATens33192.168.139.0VMnet0ens34VMne…...

被裁现状,给找工作的同学一些建议
2022 到 2023 国内知名互联网公司腾讯、阿里、百度、快手、滴滴、京东、阿里、爱奇艺、知乎、字节跳动、小米等公司均有裁员,其中有不少公司,在过去年的一整年,进行了多轮裁员,以下是网传的一张 “2022 年裁员企业名单”。 这些裁…...

编程到底难在哪里?
编程是一门非常有挑战性的技术,能够让人们使用计算机来完成各种任务。它不仅需要掌握各种计算机语言和框架,还需要在实际应用中充分发挥自己的专业知识和创造力。 然而,对于初学者来说,在编程过程中遇到的难点可能是多方面的。以…...

C++ 仿函数(一)
目录 一、仿函数是什么? 二、仿函数的特点 1.仿函数在使用时,可以像普通函数那样调用, 可以有参数,可以有返回值 2.仿函数超出普通函数的概念,可以有自己的状态 编辑3.仿函数可以作为参数传递。 三、谓词 一元谓词示例&a…...

MATLAB连续LTI系统的时域分析(十)
目录 1、实验目的: 2、实验内容: 1、实验目的: 1)掌握利用MATLAB对系统进行时域分析的方法; 2)掌握连续时间系统零输入响应的求解方法; 3)掌握连续时间系统零状态响应、冲激响应和…...
HBuilderX使用
HBuilderX使用(Vue前后端分离) 概述:DCloud开发者后台 DAccount Service 1、官网下载开发工具:HBuilderX-高效极客技巧 注意:安装目录路径中不能出现中文特殊字符,否则会造成项目无法编译。比如C:/Progr…...
【JavaSE】多态(多态实现的条件 重写 向上转移和向下转型 向上转型 向下转型 多态的优缺点 避免在构造方法种调用重写的方法)
文章目录 多态多态实现的条件重写向上转移和向下转型向上转型向下转型 多态的优缺点避免在构造方法种调用重写的方法 多态 一种事物,多种形态。 多态的概念:去完成某个行为,当不同对象去完成时会产生出不同的状态。 多态实现的条件 1.必须…...
MySQL学习---13、存储过程与存储函数
1、存储过程概述 MySQL从5.0版本开始支持存储过程和函数。存储过程和函数能够将负杂的SQL逻辑封装在一起,应用程序无序关注存储过程和函数内部复杂的SQL逻辑,而只需要简单的调用存储过程和函数就可以。 1.1 理解 含义:存储过程的英文是Sto…...

Mysql日志管理、备份与恢复
文章目录 一、Mysql日志管理1.mysql日志2.日志种类3.日志的查询4.配置日志文件 二、Mysql备份与分类1.数据备份的重要性 一、Mysql日志管理 1.mysql日志 Mysql的日志默认保存位置为/usr/local/mysql/date,Mysql的日志配置文件为/etc/my.cnf,里面有一个…...

STM32单片机声控语音识别RGB彩灯多种模式亮度可调WS2812彩灯
实践制作DIY- GC0129-语音识别RGB彩灯 一、功能说明: 基于STM32单片机设计-语音识别RGB彩灯 二、功能介绍: STM32F103C系列最小系统板5VUSB电源64个灯珠的WS2812灯板1个开关键(3档亮度调节)1个模式切换键(白灯 红灯…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
