【一文吃透归并排序】基本归并·原地归并·自然归并 C++
目录
- 1 引入情境
- 基本归并排序实现 C++
- 2 原地归并排序
- 2-1 死板的解法
- 2-2 原地工作区
- 2-3 链表归并排序
- 3 自底向上归并排序
- 4 两路自然归并排序
- 4-1 形式化描述
- 4-2 代码实现
1 引入情境
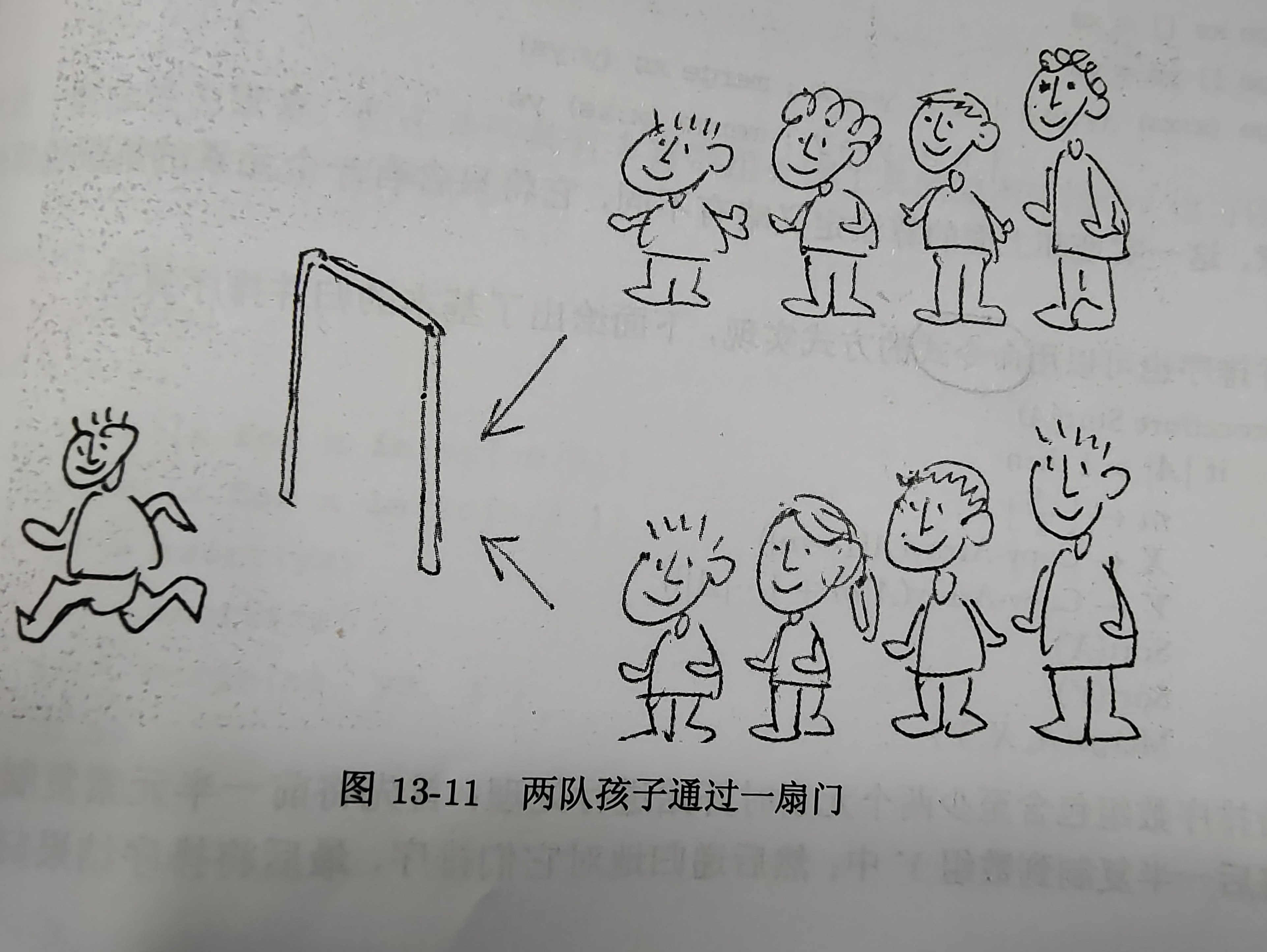
归并思想:假设有两队小孩,都是从矮到高排序,现在通过一扇门后合并为一队。要求:任何孩子,只有所有比它矮的孩子通过后,才能通过。
function merge_sort(A):if len(A) > 1 thenm = floor(len(A)/2) # 获取中心点X = copy_array(A,0,m)Y = copy_array(A,m+1,len(A)-1) #拆成差不多的两半merge_sort(X)merge_sort(Y) # 分别排序merge(A,X,Y) # 合并
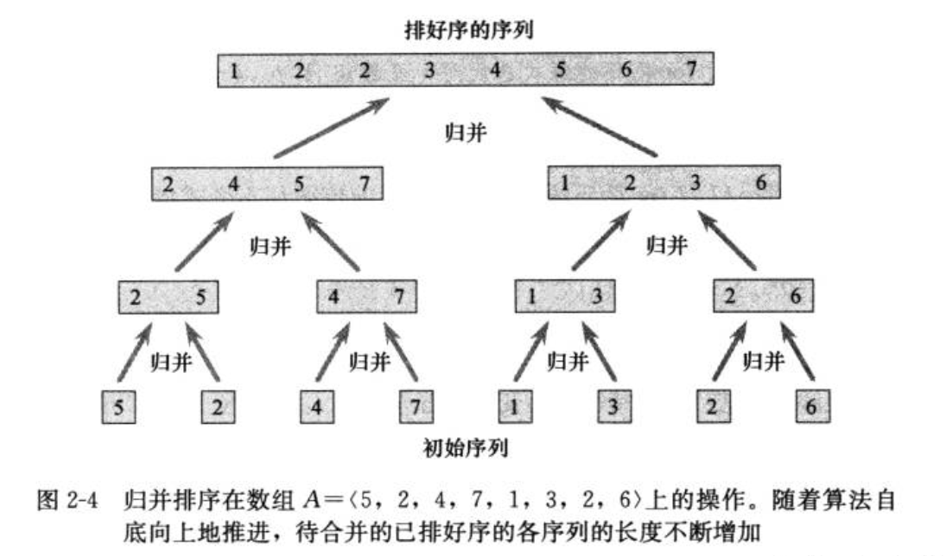
假如我理解了上面归并,但是,在排序之前,怎么得到有序的两个队列呢?注意到,伪代码的出口是 l e n ( A ) ≤ 1 len(A) \leq 1 len(A)≤1 就会返回,即一个数本身有序。当它拆分到自然有序,返回头开始合并,直接上图:
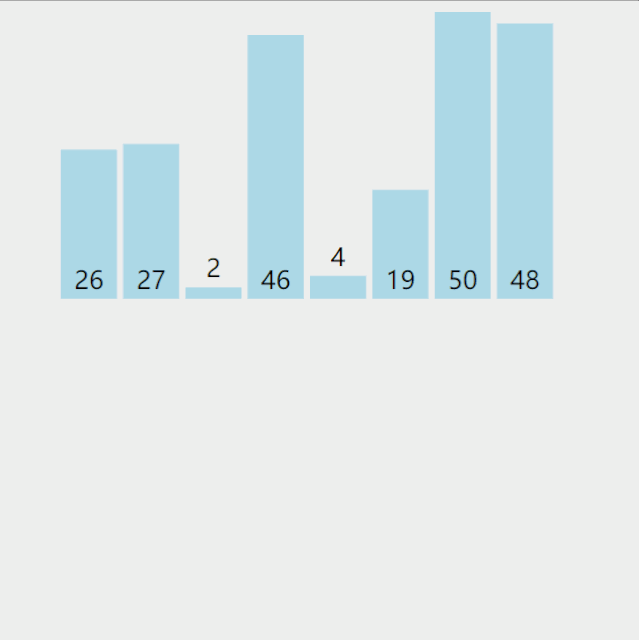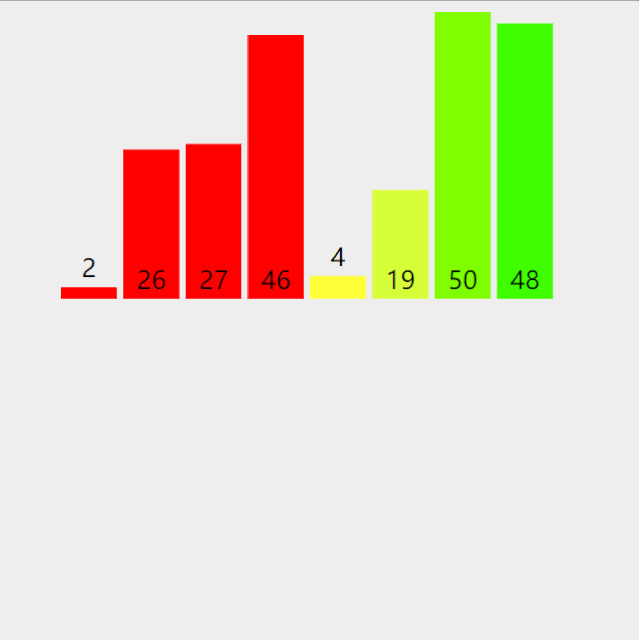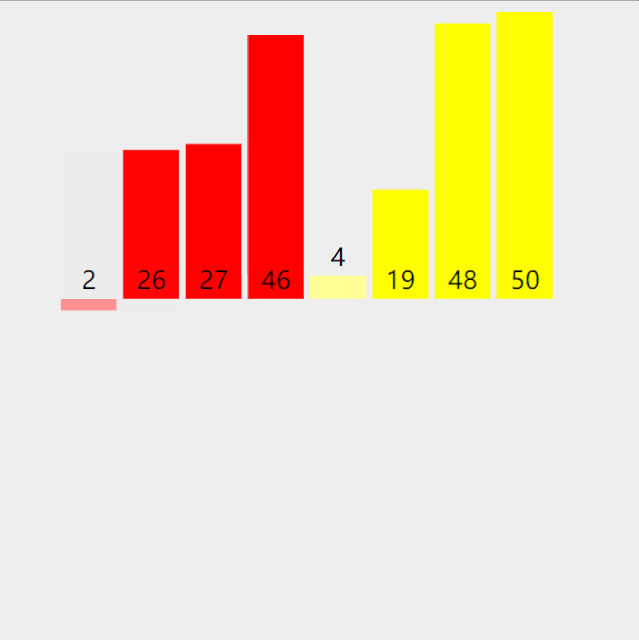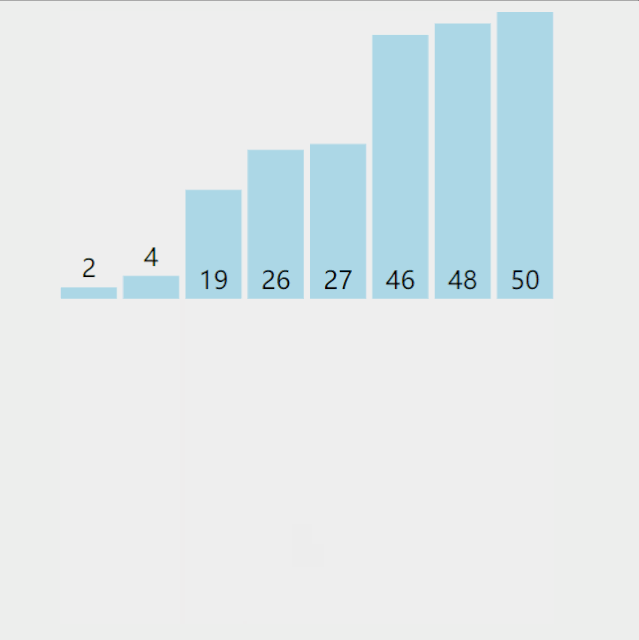
只剩下一个问题,merge(A,X,Y)是怎么做的?简单的理解,每次比较X,Y头部,选一个最小的放到目标有序数组A的队尾即可;若一队为空,另一队还有剩余就直接放到A的队尾。给出伪代码描述:
function Merge(A,X,Y):i=1,j=1,k=1xlen=|X|ylen=|Y|# 从队伍头部选一个最小的放到目标队伍末尾while i<= xlen and j <=ylen doif X[i] <= Y[i] thenA[k] = X[i]i = i + 1elseA[k] = Y[j]j = j + 1k = k + 1# 处理剩余的部分,放到末尾while i <= xlen doA[k] = X[i]k = k + 1while j <= ylen doA[k]= Y[j]j = j + 1
关于时间复杂度,设排序用时为 T ( N ) T(N) T(N),则递归开销为:
T ( N ) = T ( N 2 ) + T ( N 2 ) + c N T(N) = T(\frac {N} {2})+T(\frac {N} {2})+cN T(N)=T(2N)+T(2N)+cN
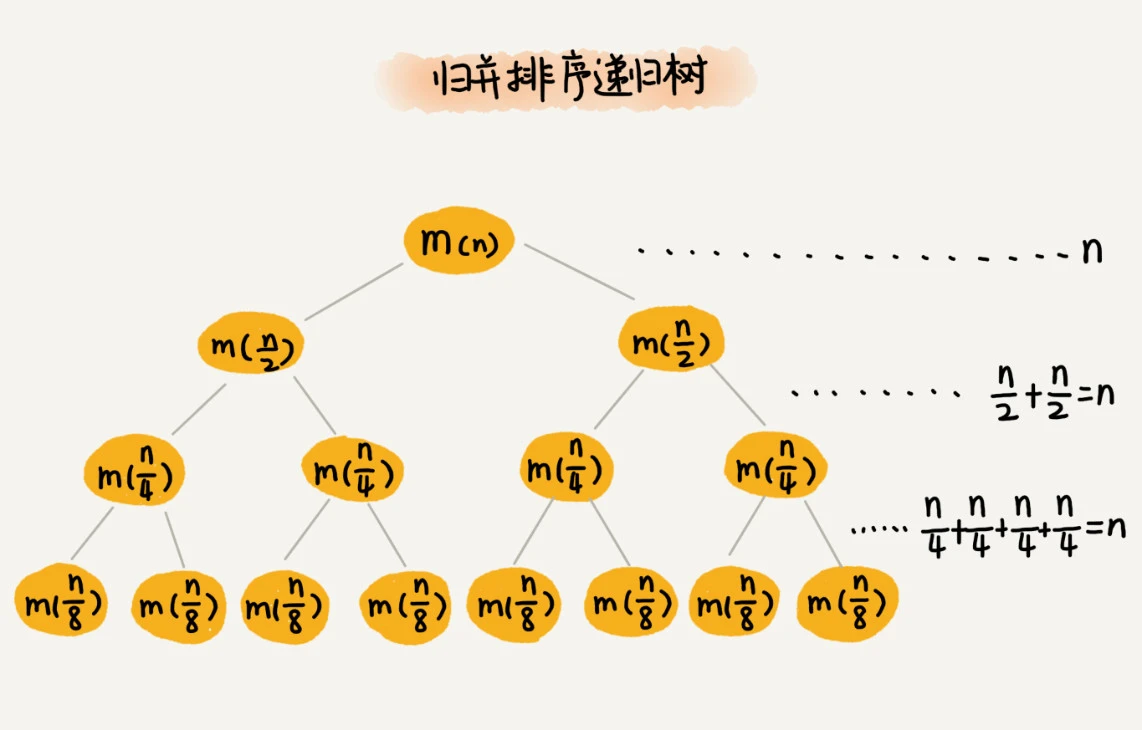
对两半分别排序是 2 T ( N 2 ) 2T(\frac {N} {2}) 2T(2N), c n cn cn是合并两个队列用时,解开后是O(NlgN)。另一种直观理解的方式如下图,拆半分层最多是 l g N lgN lgN层,每层归并都是O(N),相乘即可。
基本归并排序实现 C++
在实现之前,我们加一个小改进,在每队队伍加入一个哨兵:正无穷大(如果是非递增是负无穷),于是,merge的过程无需另行考虑剩余部分。
# 加入正无穷哨兵,会让一个较短的队列的下标阻塞在末尾
function merge(A,X,Y):append(X,INF) # 在队列尾加入哨兵,正无穷INFappend(Y,INF)for k from 1 to A.len doif X[i] < Y[j] thenA[k]=X[i]i = i + 1elseA[k]=Y[j]j =j + 1
实现时发生了两个错误:
l+(r-l)>>1和l+(r-l)/2是不同的;l+(r-l)/2和l+((r-l)>>1)才等价- l 和 1 总是容易弄混;下载编程字体点链接source code Pro
#include <iostream>
#include <vector>
#include <string>
using namespace std;const int INF=1e5;
using Key=int;
using Array =vector<Key>;void merge(Array &A,int l,int m,int r){// 开两个队列分别放 A[l,m) A[m,r)Array X(m-l+1);//多一个哨兵的位置Array Y(r-m+1);//复制元素int i=0,j=0;for(int k=l;k<m;++k) X[i++]=A[k];for(int k=m;k<r;++k) Y[j++]=A[k];X[m-l]=INF; //设置哨兵Y[r-m]=INF;for(i=0,j=0;l<r;++l){A[l]=X[i] < Y[j] ? X[i++]:Y[j++];}
}// A[l,r)
void merge_sort(Array &A,int l,int r){if(r-l>1){int m = l+(r-l)/2; // 防止溢出merge_sort(A,l,m);merge_sort(A,m,r);merge(A,l,m,r);}
}static void see_array(string arr_info,const Array &A){cout<<arr_info <<" { ";for(auto& item:A){cout<<item<<" ";}cout<<"}"<<endl;
}
void test(){Array arr{23,45,1,2,7,5,6};// merge(arr,0,3,arr.size());merge_sort(arr,0,arr.size());see_array("sorted ",arr);
}int main()
{test();return 0;
}注意到,在merge中需要申请两个数组来放数据,频繁的申请释放内存会花费大量的时间。一个解决办法是一次性申请一个和待排序数组一样大的数组B,作为工作区。这一改进将所需空间从O(NLgN)减少到了O(N),对十万个数字排序上速度提示20%~25%。C++实现如下:
#include <iostream>
#include <vector>
#include <string>
using namespace std;const int INF=1e5;
using Key=int;
using Array =vector<Key>;void merge(Array &A,Array &B,int l,int m,int r){// 合并 A[l,m) A[m,r) 到 B,再复制回来int i,j,k;// 记录两个队列的起点i=k=l;j=m;// 归并while(i<m && j<r){B[k++]=A[i]<A[j] ? A[i++]:A[j++];}// 收尾工作while(i<m) B[k++]=A[i++];while(j<r) B[k++]=A[j++];for(;l<r;++l) A[l]=B[l];
}void msort(Array &A,Array &B,int l,int r){int m;if(r-l>1){m = l+(r-l)/2; // 防止溢出msort(A,B,l,m);msort(A,B,m,r);merge(A,B,l,m,r);}
}// A[l,r)
void merge_sort(Array &A,int l,int r){Array B(r-l); //申请一个同样大小的工作区msort(A,B,l,r);
}static void see_array(string arr_info,const Array &A){cout<<arr_info <<" { ";for(auto& item:A){cout<<item<<" ";}cout<<"}"<<endl;
}
void test(){Array arr{23,45,1,2,7,5,6};// merge(arr,0,3,arr.size());merge_sort(arr,0,arr.size());see_array("sorted ",arr);
}int main()
{test();return 0;
}
2 原地归并排序
不带优化的基本实现需要空间O(NLgN),使用工作区也需要O(N),可以不用额外空间原地排序吗?
2-1 死板的解法
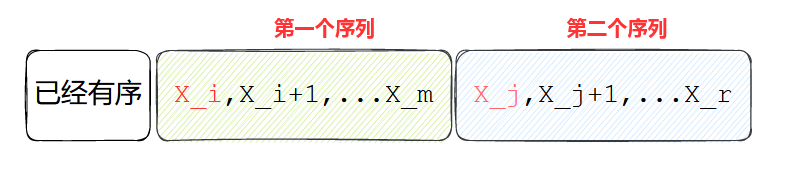
如下图,类比插入排序,通过比较 x i x_i xi和 x j x_j xj的大小确定把谁放在当前 x i x_i xi的位置上;注意到如果 x j x_j xj是更小的那个,需要把第一个序列整体向后移动一步,即覆盖掉 x j x_j xj,这样一来归并排序降低为 O ( N 2 ) O(N^2) O(N2)。
void naive_merge(Array &A,int l,int m,int r){int i;Key tmp;for(;l<m && m<r;++l){if(!(A[l]<A[m])){tmp=A[m++]; //先保存,后覆盖for(i=m-1;i>l;--i) A[i]=A[i-1];A[l]=tmp;}}
}
2-2 原地工作区
注意,这一节有亿点点的抽象,看不懂可以跳过。原地工作区的思路是借用数组未排序的部分复用为归并的工作区,稍作思考就会发现有几个问题:
-
工作区一般是空白的,如果和未排序元素共用,会不会直接把原来的、还没有排序的数据给覆盖,造成数据丢失?
-
有序的子序列很大,自然意味着剩余未排序的空间小,那用这么小的工作区能完成归并任务吗?是不是和有序的子数组也会重叠呢?
先记下这些问题并直接给出方案,并逐渐改进使问题得到应对。
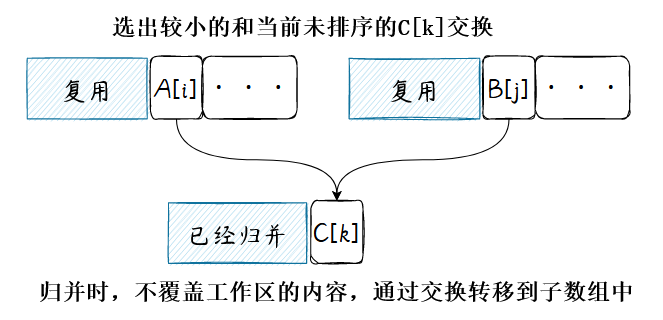
核心操作就是交换未排序的数据到子序列中,伪代码描述:
function merge(A,[i,m),[j,n),k):while i<m and j <n do if A[i]<A[j] thenswap(A[k],A[i])i =i+1else swap(A[k],A[j])j =j+1k=k+1while i<m doswap(A[k],A[i])i=i+1k=k+1while j<n doswap(A[k],A[j])j=j+1k=k+1
考虑问题2,在工作区>=待归并元素长的条件下,容易实现数组的一半有序,因为可以拿另一半作为工作区。接下来的问题是,剩下的一半怎么搞?再递归呢?如果直接归并1/4和1/2,未排序的复用空间明显不够用。
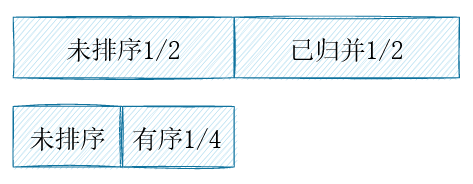
实际上,工作区可以和任何一个有序的子数组重叠,但是需要保证,尚未归并的元素不会被覆盖。所以,当归并1/4和1/2的元素时,我们可以把工作区放在正中间,允许它和有序的子数组重叠。
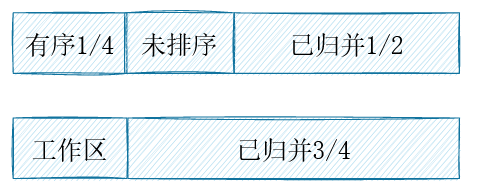
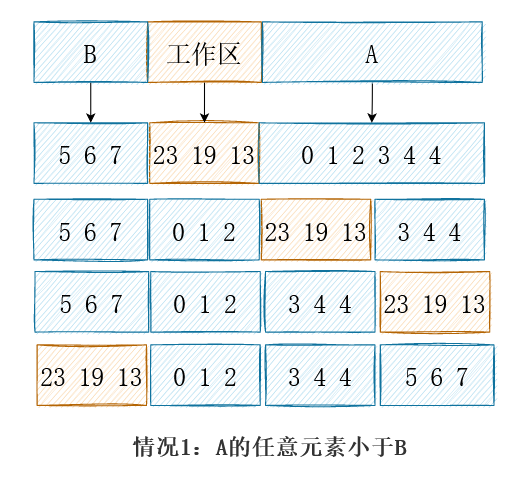
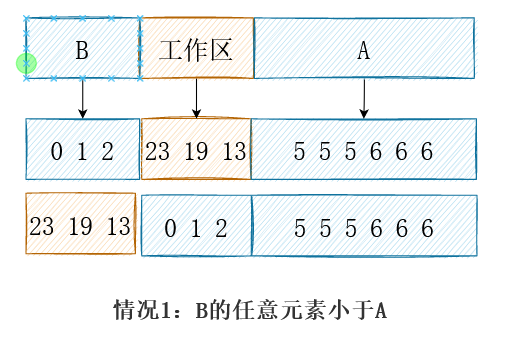
其他正常的例子与特殊情况均可保证工作区被换到左侧。于是算法明确了:总是重复对未排序部分的前1/2进行排序,从而将有序的结果交换到前一半,而使得工作区位于中间。渐渐当工作区足够小,剩余一个元素等价于插入排序;实际上对于最后几个元素(20以内)完全可以直接插入排序。伪代码描述如下:
function sort(A,l,r)if r-l>0 thenm = floor((l+r)/2)w = l+r-m # 工作区的起点sort1(A,l,m,w) # 保证后一半元素有序while w -l >1 do # 工作区间不为空nr = ww = ceil((l+nr)/2)sort1(A,w,nr,l) # 同样递归对后1/2排序后放到前面merge(A,[l,l+nr-w],[nr,r],w)## 改用插入排序for i from w down-to l doj =iwhile j <= r and A[j]<A[j-1] doswap(A[j],A[j-1])j=j+1#反向调用sort 用于交换工作区和有序部分
function sort1(A,l,r,w)if r-l > 0 thenm = floor((l+r)/2)sort(A,l,m)sort(A,m+1,r)merge(A,[l,m],[m+1,r],w) #排序并放到w开始的位置else #将所有元素交换到工作区while l<=r doswap(A[l],A[w])l =l+1w =w+1
注意虽然实现了原地归并,即O(1)的空间复杂度,但多了不少额外的交换操作。和使用额外工作区的版本相比,对十万个数字排序,速度下降了60%。C++ 详细实现如下:
#include <iostream>
#include <cmath>
#include <ctime> //随机数组using namespace std;using Key = int;// 定于一个区间
struct Range
{int l, r;Range(int a, int b) : l(a), r(b) {}void set(int left, int right){l = left;r = right;}int size(){return r - l;}
}; //[l,r);// 封装C语言的数组
struct Array
{Key *arr;int len;Array(int l) : len(l){arr = (Key *)malloc(sizeof(Key) * len);srand(time(NULL));static const int M=15; //在1~M范围内生成随机数for (int i = 0; i < len; i++){at(i) = rand() % M + 1;}}Key &operator[](int i){return *(arr + i);}Key &at(int i){return *(arr + i);}void swap(int i, int j){Key tmp = at(i);at(i) = at(j);at(j) = tmp;}void exchange(Array &B){Key *tmp = arr;arr = B.arr;B.arr = tmp;}void show(const char info[]=""){cout<<info<<"[";for (size_t i = 0; i < len; i++){cout<<at(i)<<" ";}cout<<"]."<<endl;}
};/// @brief 将数组A的两个区间的内容归并到start开始的区域
/// @param A 原数组
/// @param X 原数组的一个区间
/// @param Y 另一个区间
/// @param start 存放归并结果的开始位置
void merge(Array &A, Range &X, Range &Y, int start)
{while (X.l < X.r && Y.l < Y.r){int now = A[X.l] < A[Y.l] ? X.l++ : Y.l++;A.swap(start++, now);}while (X.l < X.r)A.swap(start++, X.l++);while (Y.l < Y.r)A.swap(start++, Y.l++);
}void sort(Array &A, int l, int r, int w);
void merge_sort(Array &A, int l, int r)
{int m, n, w;if (r - l > 1){m = l + (r - l) / 2; // midw = l + r - m; // 工作区的终点+1sort(A, l, m, w); // 将前一半排序放到后一半//[l,w]当前待排序的区间while (w - l > 2){n = w;w = l + (n - l + 1) / 2;sort(A, w, n, l); // 排序后一半放到前面Range X(l, l + n - w), Y(n, r);merge(A, X, Y, w); // 将两头有序数组合并}// 剩下一两个数作插入排序for (n = w; n >= l; --n){for (m = n; m < r && A[m] < A[m - 1]; ++m){A.swap(m, m - 1);}}}
}/// @brief 把A[l,r)排序后,放到从下标w开始的区域
void sort(Array &A, int l, int r, int w)
{int m;if (r - l > 1){m = l + (r - l) / 2;merge_sort(A, l, m);merge_sort(A, m, r);Range X(l, m), Y(m, r);merge(A, X, Y, w);}else{while (l < r){A.swap(l++, w++);}}
}void test()
{int len = 8;Array A(len);A.show("srcArr ");// test sort// sort(A,0,3,3);merge_sort(A, 0, len);A.show("sorted ");
}int main()
{test();return 0;
}2-3 链表归并排序
和数组存储类似,链表也需要均分为两个差不多长的子序列,这里使用一种奇偶分割法,简单说,从原链表头部摘下节点,交替放到两个不同的子链表中。伪代码说明:
function split(L):(A,B) =(null,null)while L not null doptr = L # 当前头结点L = next(L) # 头指针后移A = link(p,A) #将p放到链表A的头部swap(A,B) # 交换,下次换B被插入新元素return (A,B)
C++ 详细实现如下:
#include <iostream>
#include <vector>
#include <string>
using namespace std;const int INF=1e5;
using Key=int;
using Array =vector<Key>;struct Node{Key val;struct Node* nxt;Node(Key k,struct Node* next=nullptr):val(k),nxt(next){}
};using Nptr=struct Node* ;Nptr link(Nptr pre,Nptr old_head){pre->nxt=old_head;return pre;
}Nptr mk_list(const Array &A){Nptr head=new Node(-1);Nptr p=head;for(auto &x:A){Nptr now=new Node(x);p->nxt=now;p=now;}return head->nxt;
}Nptr merge(Nptr ap,Nptr bp){Nptr head=new Node(-1);//哨兵,头结点Nptr p=head;while(ap && bp){if(ap->val<bp->val){link(p,ap);ap=ap->nxt;}else{link(p,bp);bp=bp->nxt;}p=p->nxt;}if(ap) link(p,ap);if(bp) link(p,bp);return head->nxt;
}Nptr msort(Nptr L){Nptr p, ap,bp;if(!L || !L->nxt) return L;ap=bp=nullptr;while(L){p=L;L=L->nxt;ap=link(p,ap);swap(ap,bp);}ap=msort(ap);bp=msort(bp);return merge(ap,bp);
}void test_list(){Array A{23,7,1,56,23,8,31};Nptr l=mk_list(A);l=msort(l);Nptr p=l;while(p){cout<<p->val<<endl;p=p->nxt;}
}int main()
{test_list();return 0;
}
3 自底向上归并排序
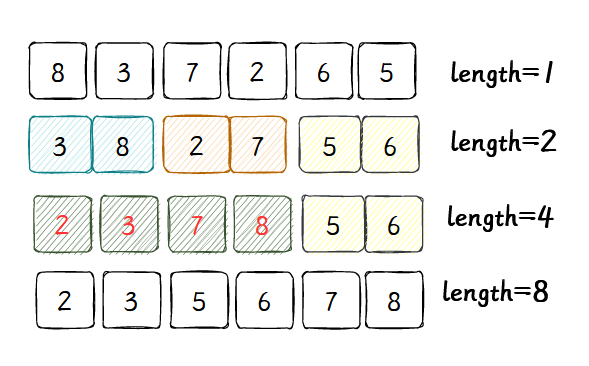
不从整体开始切分,而是一开始把每一个元素当成一个列表,然后,自底向上地合并相邻的列表,重复利用开始的那张图。注意到,因为不同切分数组,可以直接迭代,无需递归。

- 首先获得N个子列表,每个子列表一个元素;
- 将相邻的两个子序列合并,得到 n / 2 n/2 n/2个长度为2的子序列;重复这个过程,直到整体有序。
伪代码描述:
function sort(A):B = {} # 存放列表的列表,设下标从1开始for each a in A doB.append({a}) # 存入N个长度为1的子列表N = B.lengthwhile(N>1){for i from 1 to floor(N/2) doB[i] = merge(B[2i-1],B[2i]) # 每次取头两个合并if Odd(N) thenB[ceil(N/2)] = B[N] # 处理落单的N = ceil(N/2) # 向上取整if B is empty thenreturn {}return B[1]
严蔚敏的《数据结构(C语言版)》给出一种实现如下,写得真好:
/********************************************************
*函数名称:Merge
*参数说明:pDataArray 无序数组;* int *pTempArray 临时存储合并后的序列* bIndex 需要合并的序列1的起始位置* mIndex 需要合并的序列1的结束位置并且作为序列2的起始位置* eIndex 需要合并的序列2的结束位置
*说明: 将数组中连续的两个子序列合并为一个有序序列
*********************************************************/
void Merge(int* pDataArray, int *pTempArray, int bIndex, int mIndex, int eIndex)
{int mLength = eIndex - bIndex; //合并后的序列长度int i = 0; //记录合并后序列插入数据的偏移int j = bIndex; //记录子序列1插入数据的偏移int k = mIndex; //记录子序列2掺入数据的偏移while (j < mIndex && k < eIndex){if (pDataArray[j] <= pDataArray[k]){pTempArray[i++] = pDataArray[j];j++;}else{pTempArray[i++] = pDataArray[k];k++;}}if (j == mIndex) //说明序列1已经插入完毕while (k < eIndex)pTempArray[i++] = pDataArray[k++];else //说明序列2已经插入完毕while (j < mIndex)pTempArray[i++] = pDataArray[j++];for (i = 0; i < mLength; i++) //将合并后序列重新放入pDataArraypDataArray[bIndex + i] = pTempArray[i];
}/********************************************************
*函数名称:BottomUpMergeSort
*参数说明:pDataArray 无序数组;* iDataNum为无序数据个数
*说明: 自底向上的归并排序
*********************************************************/
void BottomUpMergeSort(int* pDataArray, int iDataNum)
{int *pTempArray = (int *)malloc(sizeof(int) * iDataNum); //临时存放合并后的序列int length = 1; //初始有序子序列长度为1while (length < iDataNum){int i = 0;for (; i + 2*length < iDataNum; i += 2*length)Merge(pDataArray, pTempArray, i, i + length, i + 2*length);if (i + length < iDataNum)Merge(pDataArray, pTempArray, i, i + length, iDataNum);length *= 2; //有序子序列长度*2}free(pTempArray);
}
几点说明:
- length代表的是单个子序列的长度;
- pTempArray 是上述文章提到的统一的工作区
- 实际排序时,并没有分为多个数组,而是只针对下标作逻辑上的合并,数据还在原来的数组中。
- 每次需要合并的两部分是
A[i,i+length) 和 A[i+length,i+2*length)注意右边界取不到。 - 下一次只需要把长度值翻倍即可,省去了许多开辟、释放空间的时间。
- 每次需要合并的两部分是
4 两路自然归并排序
从一个例子说起,如下图。虽然整个序列是混乱的,但是总有些部分是自然有序的(最差是一个数);想象一个两头都被点燃的蜡烛,同样的,我们从序列的两头同时开始寻找一个非递减的序列,如图中左右两端的 [8,12,14]和[15,7],合并到最右端;下一次找到后,合并到最最左端,这样做是为了平衡。
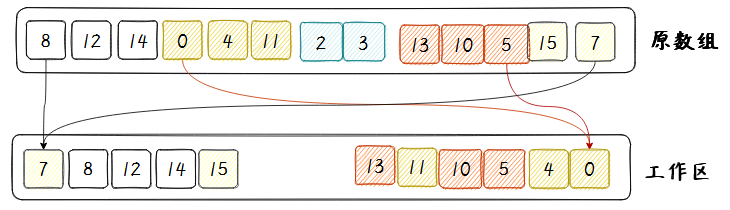
注意,上图数据归并后,左边是非递减,右边是非递增;且并不是一次完成所有的数据有序,而是多段有序,下面会进一步解释。
4-1 形式化描述
自然归并排序的不变性质,如下图所示:

- 任何时候,a之前和d之后的元素已经被扫描并归并到工作区的左右两端。
- 每次都需要将非递减子序列
[a,b)扩展到最长,同样的将[c,d)向左扩展到最长。 f(front)之前和r(rear)之后的元素是已经处理过的,可能包含若干有序的子序列,并非直接有序。- 奇数轮归并到
f这一边,偶数轮归并到r那一边。 - 关键中的关键,当扫描一轮后,原数组和工作区交换,继续归并,此时原数组(指针)指向工作区,且有序的子序列明显增多。
给出伪代码描述,如果还是看不明白建议抄一下伪代码:
function sort(A):if A.length > 1 thenn = A.lengthB = creat-array(n) # 创建工作区loop [a,b) = [1,1)[c,d) = [n+1,n+1)f = 1,r = n # 工作区的首尾指针t = False # 控制从f还是r归并while b < c dorepeat b = b+1until b >= c || A[b]<A[b-1]repeatc = c-1until c<=b || A[c-1]<A[c]if c < b then # 避免overlap 重叠c = bif b-a >=n then # 整个数组已经有序return Aif t then # 从front归并f = merge(A,[a,b),[c,d),B,f,1)else #从rear归并r = merge(A,[a,b),[c,d),B,r,-1)a = bd = ct = not t # 换方向exchange A<->B # 关键的一步,切换工作区return A# w 是工作区归并边界的下标 f 或 r
# det 表示方向 +1 或 -1
function merge(A,[a,b),[c,d),B,w,det):while a<b and c<d doif A[a]<A[d-1] thenB[w] = A[a]a =a + 1elseB[w] = A[d-1]d = d-1w = w+detwhile a < b doB[w] = A[a]a=a+1w=w+det while c < d doB[w]=A[d-1]d=d-1w=w+detreturn w
4-2 代码实现
一些说明:
- 为了提高可读性,封装了C语言下的数组指针和区间类Range
- 参数很多时,建议先声明,然后统一赋值;注意到下标得到赋值在每一轮都需要更新
#include <iostream>
#include <cmath>
#include <ctime> //随机数组using namespace std;using Key = int;// 定义一个左闭右开的区间
struct Range{int l,r;void set(int left,int right){l=left;r=right;}int size(){return r-l;}
};//[l,r);// 封装C语言的数组
struct Array
{Key* arr;int len;Array(int len):len(len){arr=(Key*) malloc(sizeof(Key)*len);}Key& operator[](int i){return *(arr+i);}Key& at(int i){return *(arr+i);}void exchange(Array &B){Key* tmp=arr;arr=B.arr;B.arr=tmp;}
};/// @brief 合并A的两个区间 Up Down到工作区B的w开始处
/// @param A 源序列
/// @param Up 位于左边的非递减序列
/// @param Down 位于右边的非递增序列
/// @param B 工作区,和源序列同样大
/// @param w 工作区的归并起点
/// @param det 控制w的增长方向,+1 or -1
/// @return 归并后的w值
int merge(Array &A, Range &Up, Range &Down,Array &B, int w, int det)
{for(;Up.l<Up.r && Down.l<Down.r;w+=det){B[w]= (A[Up.l]<A[Down.r-1]) ? A[Up.l++]:A[--Down.r];}// 收尾工作for(;Up.l<Up.r;w+=det){B[w]=A[Up.l++];}for(;Down.l<Down.r;w+=det){B[w]=A[--Down.r];}return w;
}Array& merge_sort(Array &A){if(A.len<2) return A;Array B(A.len); //申请工作区Range Up,Down; //左边的非递减区间,右边的非递增区间int front,rear,dir;//工作区的前后指针和方向for(;;){Up.set(0,0);Down.set(A.len,A.len);front=0;rear=A.len-1;dir=1;while(Up.r<Down.l){do{++Up.r; // 寻找非递减序列的右边界}while(Up.r<Down.l && A[Up.r-1]<=A[Up.r]);do{--Down.l;}while(Up.r<Down.l && A[Down.l]<=A[Down.l-1]);if(Down.l<Up.r){Down.l=Up.r; //消除可能的重叠}// 出口,已经有序if(Up.size()>=A.len){return A;}if(dir){front=merge(A,Up,Down,B,front,1);}else{rear=merge(A,Up,Down,B,rear,-1);}Up.l=Up.r;Down.r=Down.l;// 跳过已经扫描的部分dir=!dir;}A.exchange(B);}return A;
}void test(){const int len=7;Array A(len);srand(time(NULL));for(int i=0;i<len;i++){A.at(i)=rand()%25+1;cout<<A.at(i)<<" ";}cout<<endl;merge_sort(A);for(int i=0;i<len;i++){cout<<A.at(i)<<" ";}cout<<endl;
}int main()
{test();return 0;
}相关文章:

【一文吃透归并排序】基本归并·原地归并·自然归并 C++
目录 1 引入情境基本归并排序实现 C 2 原地归并排序2-1 死板的解法2-2 原地工作区2-3 链表归并排序 3 自底向上归并排序4 两路自然归并排序4-1 形式化描述4-2 代码实现 1 引入情境 归并思想:假设有两队小孩,都是从矮到高排序,现在通过一扇门后…...

读《Spring Boot 3核心技术与最佳实践》有感
我是谁? 👨🎓作者:bug菌 ✏️博客:CSDN、掘金、infoQ、51CTO等 🎉简介:CSDN/阿里云/华为云/51CTO博客专家,C站历届博客之星Top50,掘金/InfoQ/51CTO等社区优质创作者&am…...

板子短路了?
有段时间没更新了,主要是最近有点忙,当然也因为有点“懒”。 做这行业的都知道,下半年都是比较忙的,相信大家也是! 相信做硬件的小伙伴们,遇到过短路的板子已经不计其数了。 短路带来的危害:…...

一行代码绘制高分SCI限制立方图
一、概述 Restricted cubic splines (RCS)是一种基于样条函数的非参数化模型,它可以可靠地拟合非线性关系,可以自适应地调整分割结点。在统计学和机器学习领域,RCS通常用来对连续型自变量进行建模,并在解释自变量与响应变量的关系…...
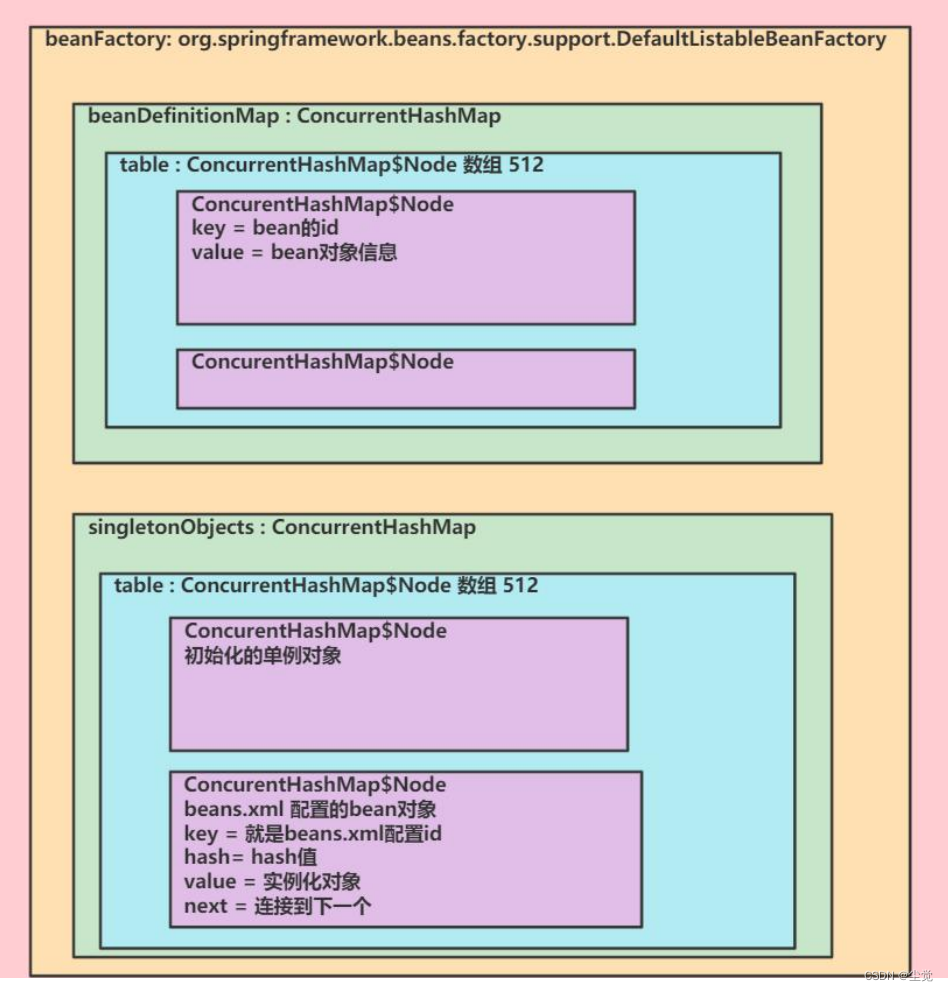
spring 容器结构/机制debug分析--Spring 学习的核心内容和几个重要概念--IOC 的开发模式--综合解图
目录 Spring Spring 学习的核心内容 解读上图: Spring 几个重要概念 ● 传统的开发模式 解读上图 ● IOC 的开发模式 解读上图 代码示例—入门 xml代码 注意事项和细节 1、说明 2、解释一下类加载路径 3、debug 看看 spring 容器结构/机制 综合解图 Spring Spr…...
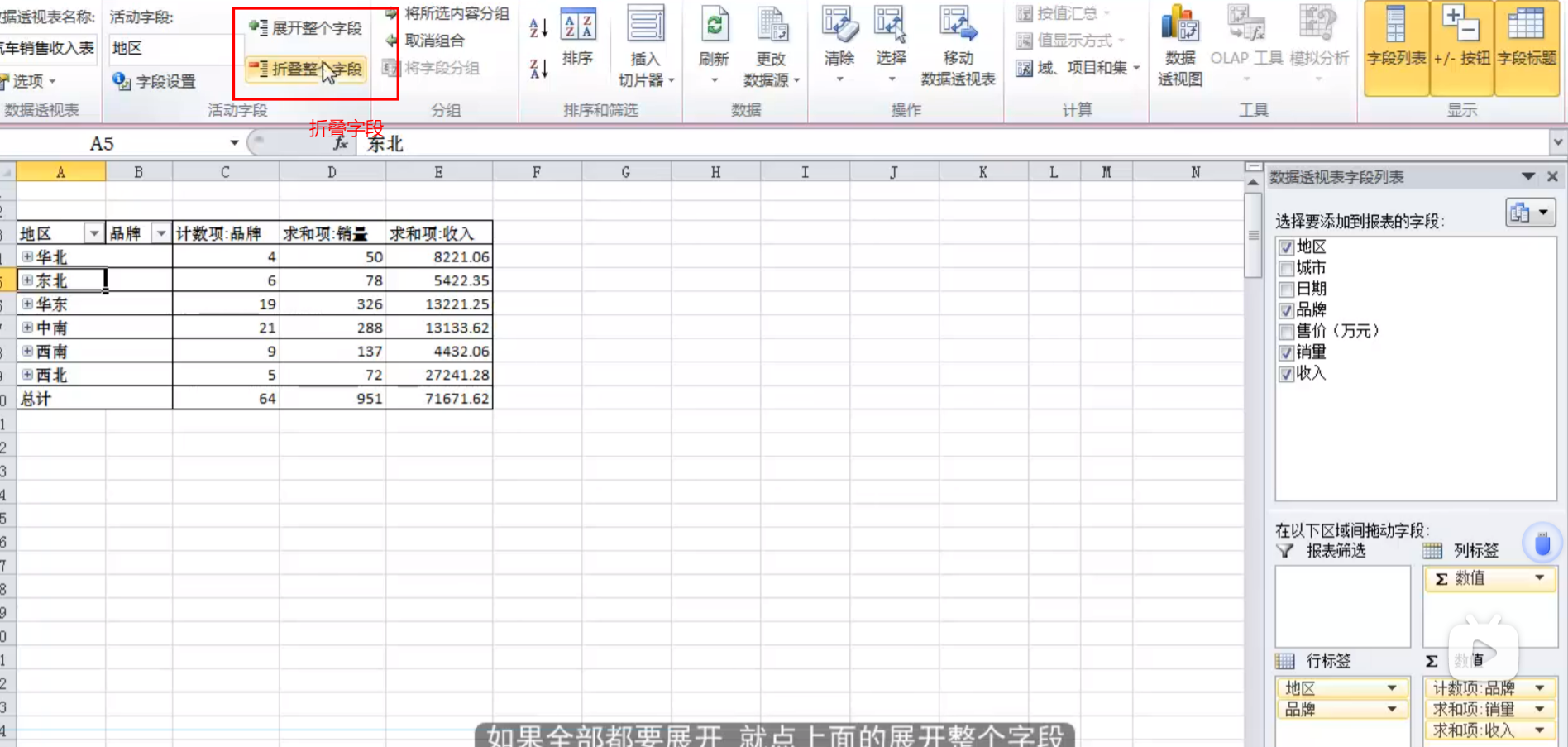
excel实战小测第四
【项目背景】 本项目为某招聘网站部分招聘信息,要求对“数据分析师”岗位进行招聘需求分析,通过对城市、行业、学历要求、薪资待遇等不同方向进行相关性分析,加深对数据分析行业的了解。 结合企业真实招聘信息,可以帮助有意转向数…...
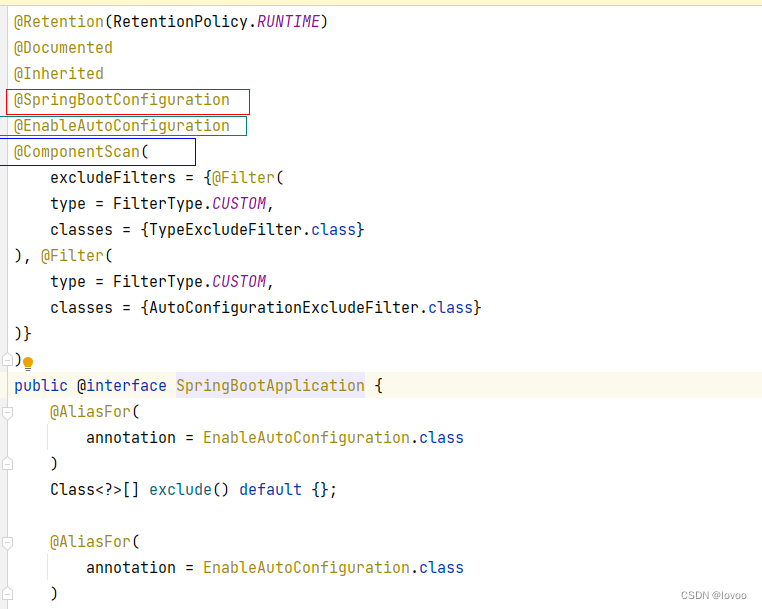
什么是SpringBoot自动配置
概述: 现在的Java面试基本都会问到你知道什么是Springboot的自动配置。为什么面试官要问这样的问题,主要是在于看你有没有对Springboot的原理有没有深入的了解,有没有看过Springboot的源码,这是区别普通程序员与高级程序员最好的…...
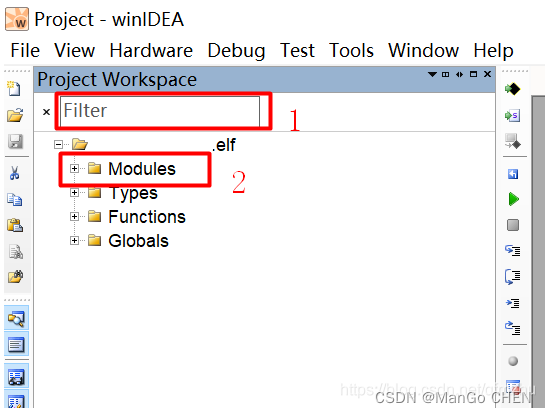
基于IC5000烧录器使用winIDEA烧写+调试程序(S32K324的软件烧写与调试)
目录 一、iSYSTEM简介二、如何使用iSYSTEM winIDEA烧写调试程序2.1 打开winIDEA:2.2 新建一个Workspace;2.3 硬件配置:2.4 选择CPU芯片型号:2.5 加载烧写文件:2.6 开始烧录程序:2.7 程序调试Debug:2.7.1 运行程序&…...
新手开始学【网络安全】要怎么入门?
前言:网络安全如何从零开始学习,少走弯路? 目录: 一,怎么入门? 1、Web 安全相关概念(2 周)2、熟悉渗透相关工具(3 周)3、渗透实战操作(5 周&…...

Linux指令 快捷键
热键 上一次我们说到了linux的基本指令,这次我们先说一下热键 TAB TAB键在linux中有什么作用呢?? 在Linux中,假设我们想要输入的指令忘记了,我们可以TAB两下,帮我们补全命令或者假如命令太多࿰…...

Testing and fault tolerence考试要点
文章目录 ATPGFault modelScanFunctional testMemory BISTLogic BISTboundary scanATEIddq testingFault tolerant designRisk analysis ATPG ATPG工作流程fault collapsing的原则 Fault model 有哪些fault model以及他们的工作原理 Scan Scan寄存器结构Scan Chain的连接方…...

记一次springboot项目漏洞挖掘
前言 前段时间的比赛将该cms作为了题目考察,这个cms的洞也被大佬们吃的差不多了,自己也就借此机会来浅浅测试下这个cms残余漏洞,并记录下这一整个流程,谨以此记给小白师傅们分享下思路,有错误的地方还望大佬们请以指正…...

R语言 | 数据框
目录 一、认识数据框 7.1 建立第一个数据框 7.2 验证与设定数据框的列名和行名 二、认识数据框的结构 三、获取数据框内容 3.1 一般获取 3.2 特殊字符$ 3.3 再看取得的数据 四、使用rbind()函数增加数据框的行数据 五、使用cbind()函数增加数据框的列数据 5.1 使用$符号…...
基于SpringBoot的招生管理系统的设计与实现
背景 本次设计任务是要设计一个招生管理系统,通过这个系统能够满足管理员和学生的招生公告管理功能。系统的主要功能包括首页、个人中心、学生管理、专业信息管理、专业报名管理、录取通知管理、系统管理等功能。 管理员可以根据系统给定的账号进行登录࿰…...
Oracle Profile详解
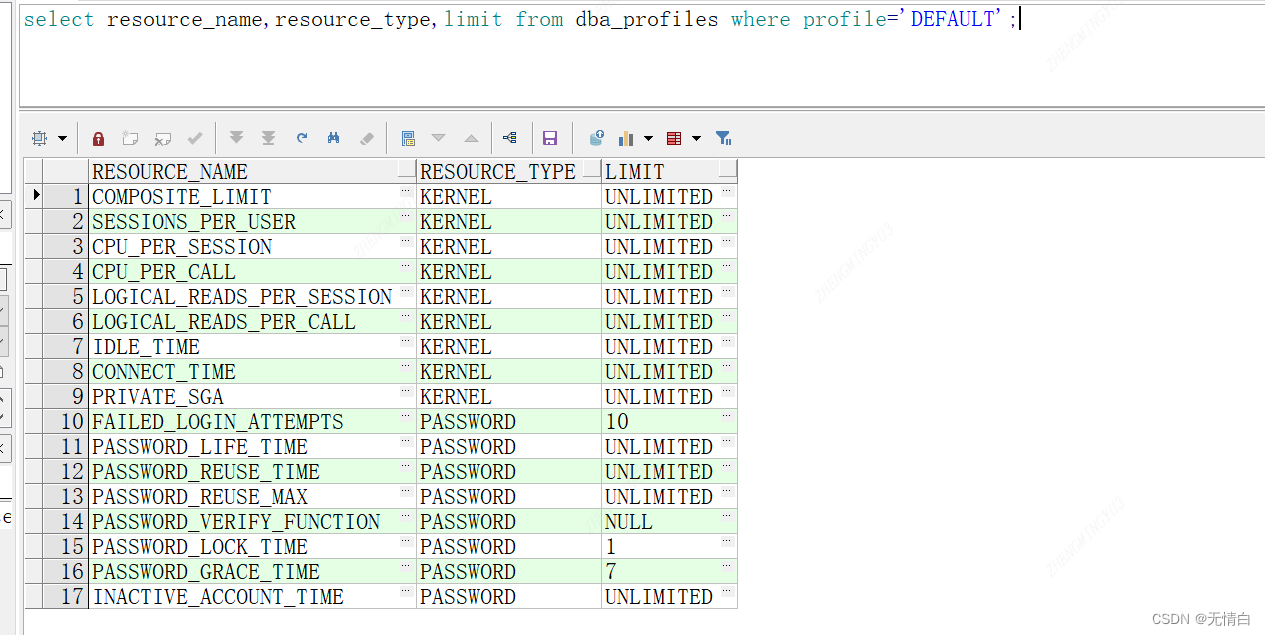
Profile的作用主要表现在三个方面 1、密码策略 2、对用户所能使用的资源进行管理 3、profile存放在数据字典里面,默认有一个名字为default的profile set linesize 160 set pagesize 30 select resource_name,resource_type,limit from dba_profiles where profile‘…...

r语言tidyverse教程:5 字符串处理stringr
文章目录 R语言系列: 编程基础💎循环语句💎向量、矩阵和数组💎列表、数据帧排序函数💎apply系列函数tidyverse:readr💎tibble💎tidyr💎dplyr💎stringr stri…...

知识变现海哥:知识变现的本质就是卖
知识变现的本质就是卖,而有人买的本质,就是你解决了某方面的需求。 好的成交,从来都是相互的, 只靠一边主动推销来维系是远远不够的。 绝对不是靠忽悠,而是靠实力。 先讲一个故事。 19世纪时,一个年轻的…...

jdbc和druid和mybatis之间的关系
第一种方式 jdbc整合了:加载数据库驱动,创建连接,写原生语句,执行,关闭这些东西. 第二种方式 mybatis对jdbc进行封装,他允许你通过配置的形式,配置数据库参数,并且允许你通过xml来写动态sql语句.if:test让你可以把sql变得灵活起来.并且还能将你的查询结果直接映射到你想要的…...
云原生Istio案例实战
目录 1 Istio监控功能1.1 prometheus和grafana1.2 访问prometheus1.3 访问grafana 2 项目案例:bookinfo2.1 理解什么是bookinfo2.2 sidecar自动注入到微服务2.3 启动bookinfo2.4 通过ingress方式访问2.5 通过istio的ingressgateway访问2.5.1 确定 Ingress 的 IP 和端…...

解读赛力斯年报:华为智选车的B面
作者 | Amy 编辑 | 德新 赛力斯,华为智选车的B面。 2021年,赛力斯SF5进入华为渠道销售,华为自此开启了智选车模式。到年末,双方更是推出AITO品牌。AITO凭借M5/M7等车型在2022年拿下了超过7.5万台的销量,成为增长最快的…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
