【ADRC控制】使用自抗扰控制器调节起动机入口压力值
以前只知道工业控制中用的是PID控制,然而最近了解到实际生产中还在使用ADRC控制,而且使用效果还优于PID控制,遂找了几篇文献学习学习。
0 引言
自抗扰控制(Active Disturbances Rejection Controller,ADRC)技术,是发扬PID控制技术的精髓并且吸取了现代控制理论,不依赖于被控对象精确模型,能够替代PID控制技术,是一种新型的实用数字控制技术。
PID控制的缺点:
①直接以 e=v−ye=v-ye=v−y 的方式产生原始误差不太合理,因为控制目标 vvv 是可以跳变的,而对象输出 yyy 是存在惯性的,不可能跳变,所以让缓变的 yyy 来跟踪能跳变的 vvv 是不合理的。
② 由于微分器物理不可实现,只能近似实现,所以产生误差的微分信号 de/dt\mathrm{d}e/\mathrm{d}tde/dt 是不合适的,并且微分信号容易被噪声干扰。
③线性组合不一定是最好的组合办法。
④误差信号 eee 的积分∫0∝e(t)dt\int\limits_0^{\propto}{e\left( t \right) \mathrm{d}t}0∫∝e(t)dt 的引入有很多负作用,其能使闭环变得迟钝,容易产生振荡。
因此,基于PID控制的思想,并且利用现代数字信号处理技术,开发出新型实用数字控制技术——ADRC自抗扰控制。
1 空气起动系统模型
空气起动系统模型见:【空气起动系统控制】使用神经网络PID调节起动机入口压力值
2 ADRC控制器设计
自抗扰控制器(ADRC)主要包括由安排过度过程减少输入对系统的冲击以及提取微分信号的跟踪微分器TD;对系统状态观测和扰动估计的扩张状态观测器ESO;实时动态反馈的状态误差反馈控制NLSEF三个部分,结构图如下图所示。
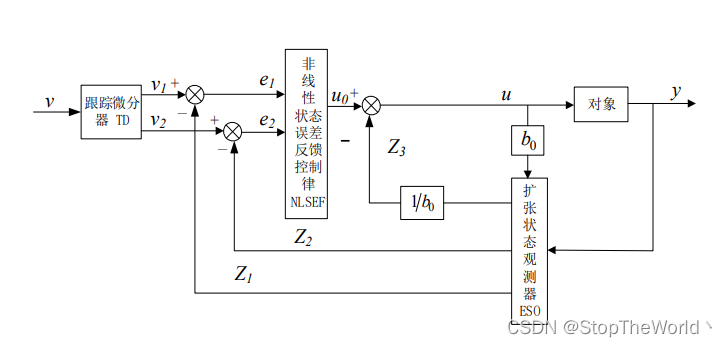
2.1 跟踪微分器TD
跟踪微分器(Tracking Differentiator)可以对输入信号进行预处理,其能够快速的跟踪给定的输入信号,并且能够通过非线性最速函数迭代的方式得到输入的微分,而不是直接应用微分器的方式得到输入的微分,减少了噪声信号的干扰。一般二阶形式如下:
{v˙1=v2v˙2=fhfh=fhan(v1−v0,v2,r,h0)\begin{cases} \dot{v}_1=v_2\\ \dot{v}_2=fh\\ fh=fhan\left( v_1-v_0, v_2, r, h_0 \right)\\ \end{cases} ⎩⎨⎧v˙1=v2v˙2=fhfh=fhan(v1−v0,v2,r,h0) v0v_0v0 输入信号,v1v_1v1 输入信号的跟踪信号,v2v_2v2 输入信号的微分信号,rrr 速度因子,h0h_0h0 滤波因子,fhanfhanfhan 为非线性的最速控制综合函数,能够实现对期望输入的平稳快速跟踪,且对输入信号的噪声具有一定的抑制效果。
fhan(v1−v0,v2,r,h0)={fsg(x,d)=(sign(x+d)−sign(x−d))/2d=rh2a0=h0x2y=x1+a0a1=d(d+8∣y∣)a2=a0+sign(y)(a1−d)/2a=(a0+y)fsg(y,d)+a2(1−fsg(y,d))fhan=−r(ad)fsg(a,d)−rsign(a)(1−fsg(a,d))fhan\left( v_1-v_0, v_2, r, h_0 \right) =\left\{ \begin{array}{c} \begin{array}{c} \begin{array}{c} \begin{array}{c} fsg\left( x,d \right) =\left( \mathrm{sign}\left( x+d \right) -\mathrm{sign}\left( x-d \right) \right) /2\\ d=rh^2\\ \end{array}\\ a_0=h_0x^2\\ \end{array}\\ y=x_1+a_0\\ \end{array}\\ \begin{array}{c} \begin{array}{c} a_1=\sqrt{d\left( d+8\left| y \right| \right)}\\ a_2=a_0+\mathrm{sign}\left( y \right) \left( a_1-d \right) /2\\ \end{array}\\ a=\left( a_0+y \right) fsg\left( y,d \right) +a_2\left( 1-fsg\left( y,d \right) \right)\\ fhan=-r\left( \frac{a}{d} \right) fsg\left( a,d \right) -r\mathrm{sign}\left( a \right) \left( 1-fsg\left( a,d \right) \right)\\ \end{array}\\ \end{array} \right. fhan(v1−v0,v2,r,h0)=⎩⎨⎧fsg(x,d)=(sign(x+d)−sign(x−d))/2d=rh2a0=h0x2y=x1+a0a1=d(d+8∣y∣)a2=a0+sign(y)(a1−d)/2a=(a0+y)fsg(y,d)+a2(1−fsg(y,d))fhan=−r(da)fsg(a,d)−rsign(a)(1−fsg(a,d))
2.2 扩张状态观测器ESO
扩张状态观测器(Extended State Observer)是将除了串联积分标准型以外的模型部分和外界扰动当作一个新的状态,进行观测。对于二阶系统,ESO 的标准形式为
{e=z1−yz˙1=z2−β01ez˙2=z3−β02fal(e,α01,δ01)+b0uz˙3=−β03faln(e,α02,δ02)\begin{cases} \begin{array}{l} \begin{array}{l} e=z_1-y\\ \dot{z}_1=z_2-\beta _{01}e\\ \end{array}\\ \dot{z}_2=z_3-\beta _{02}fal\left( e,\alpha _{01},\delta _{01} \right) +b_0u\\ \end{array}\\ \dot{z}_3=-\beta _{03}fal_n\left( e,\alpha _{02},\delta _{02} \right)\\ \end{cases} ⎩⎨⎧e=z1−yz˙1=z2−β01ez˙2=z3−β02fal(e,α01,δ01)+b0uz˙3=−β03faln(e,α02,δ02) 其中非线性函数 falfalfal 为
fal(x,α,δ)={∣x∣αsign(x),∣x∣⩾δx/δ1−α,∣x∣<δfal\left( x,\alpha ,\delta \right) =\begin{cases} \left| x \right|^{\alpha}\mathrm{sign}\left( x \right) , \left| x \right|\geqslant \delta\\ x/\delta ^{1-\alpha}, \left| x \right|<\delta\\ \end{cases} fal(x,α,δ)={∣x∣αsign(x),∣x∣⩾δx/δ1−α,∣x∣<δ β01\beta _{01}β01, β02\beta _{02}β02, …, β0n\beta _{0n}β0n 为ESO的增益,其值对ESO的观测能力和估计扰动的能力起决定性作用。eee 为观测误差,δ0i\delta _{0i}δ0i 为观测误差的线性变化区域的大小,α0i\alpha _{0i}α0i 代表误差指数变化的参数,b0b _{0}b0 为控制增益的估计值。ESO不仅能够观测出状态变量 x(n)x^{\left( n \right)}x(n) 和 znz_nzn 还能估计出系统总扰动 zn+1z_{n+1}zn+1,其中总扰动包括已建动力学模型、模型不确定性和外部干扰等因素。
2.3 非线性反馈
非线性反馈(Nonlinear State Error Feedback)是保留了PID基于误差消除误差的部分,与 PD 控制不同的是加入了非线性函数,不再是原来线性组合的方式,利用非线性函数的性质实现更高精度的控制,常用的控制器主要为:
{e1=v1−z1e2=v2−z2u0=β1fal(e1,α1,δ1)+β2fal(e2,α2,δ1)\begin{cases} e_1=v_1-z_1\\ e_2=v_2-z_2\\ u_0=\beta _1fal\left( e_1,\alpha _1,\delta _1 \right) +\beta _2fal\left( e_2,\alpha _2,\delta _1 \right)\\ \end{cases} ⎩⎨⎧e1=v1−z1e2=v2−z2u0=β1fal(e1,α1,δ1)+β2fal(e2,α2,δ1) 其中,viv_ivi 为TD输出信号,ziz_izi 为ESO的输出,βi\beta_iβi 为非线性反馈的增益,falfalfal 函数见上。
2.4 扰动补偿
扰动补偿部分是 ADRC 控制器最为核心思想。通过 ESO 实时观测扰动并在控制输入端实时补偿,在扰动对系统产生影响前补偿到控制输入端。针对二阶系统,z3z_3z3 是对总扰动的估计,所以控制量为
u=u0−z3/b0u=u_0-z_3/b_0 u=u0−z3/b0 其中,b0b_0b0 为补偿因子,与ESO中的参数 b0b_0b0 一致,适当调节可得到最终的控制效果。
另外,TD、ESO、NLSEF的参数整定方法见空气起动系统仿真下面的 NLSEF.m 脚本说明。
3 仿真结果
将本文的控制方法与之前使用的PID控制器、RBF-PID控制器进行对比,在相同的参数下,仿真结果如下
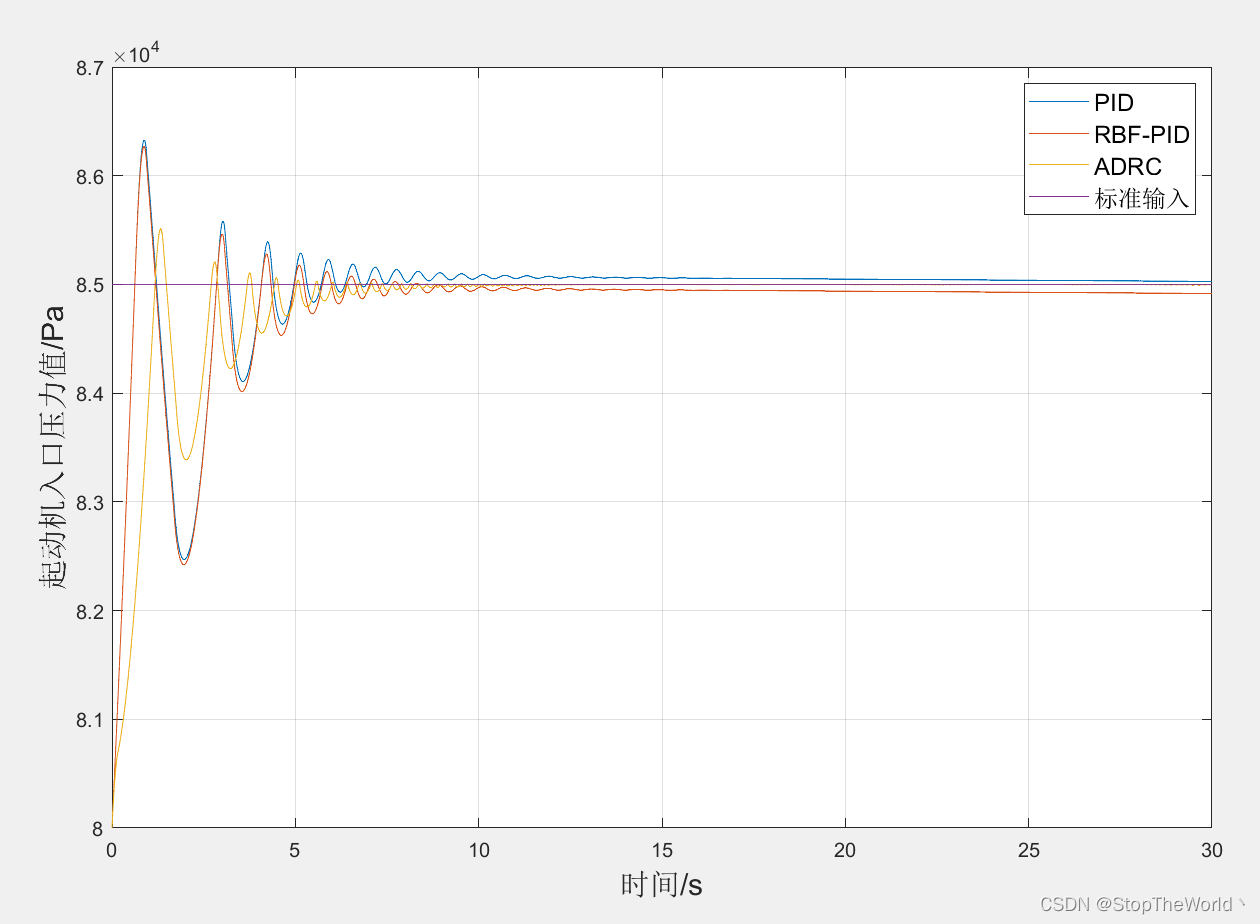
结论:由图可得,ADRC控制器相比于另外两种控制器,其超调量更小,稳态误差也更小,调节时间也更短,有明显的性能改善,初步验证了ADRC控制在理论上的可行性。
4 未来工作
由于ADRC控制相比PID控制在基础理论层面和仿真层面上有明显的改善,所以下一步工作准备将ADRC控制应用于实际工程上,使用PLC程序编写ADRC控制代码以替换掉原来的PID控制程序,看看ADRC的实际控制结果究竟如何。
相关文章:

【ADRC控制】使用自抗扰控制器调节起动机入口压力值
以前只知道工业控制中用的是PID控制,然而最近了解到实际生产中还在使用ADRC控制,而且使用效果还优于PID控制,遂找了几篇文献学习学习。 0 引言 自抗扰控制(Active Disturbances Rejection Controller,ADRC)…...
)
剑指 Offer Day2——链表(简单)
目录剑指 Offer 06. 从尾到头打印链表剑指 Offer 24. 反转链表剑指 Offer 35. 复杂链表的复制剑指 Offer 06. 从尾到头打印链表 原题链接:06. 从尾到头打印链表 最容易想到的思路就是先从头到尾打印下来,然后 reverse 一下,但这里我们使用递归…...

Final Cut Pro 10.6.5
软件介绍Final Cut Pro 10.6.5 已通过小编安装运行测试 100%可以使用。Final Cut Pro 10.6.5 破解版启用了全新的矩形图标,与最新的macOS Ventura设计风格统一,支持最新的macOS 13 文图拉系统,支持Apple M1/M2芯片。经过完整而彻底的重新设计…...
Modelsim仿真操作指导
目录 一、前言 二、仿真分类 三、RTL级仿真 3.1创建库 3.2 仿真配置设置 3.3 运行仿真 四、常见问题 4.1 运行仿真时报错“cant read "Startup(-L)": no such element in array” 4.2 运行仿真时无任何报错,但object窗口为空,可正常运…...

你知道这20个数组方法是怎么实现的吗?
前言你们一定对JavaScript中的数组很熟悉,我们每天都会用到它的各种方法,比如push、pop、forEach、map……等等。但是仅仅使用它就足够了吗?如此出色,您一定不想停在这里。我想和你一起挑战实现20数组方法的功能。1、forEachforEa…...

《系统架构设计》-01-架构和架构师概述
文章目录1. 架构的基本定义1.1 架构组成理论1.1.1 系统元素1)概念2)静态结构和动态结构1.1.2 基本系统属性1.1.3 设计和发展原则1.2 架构的决策理论1.2.1 统一软件过程(Rational Unified Process,统一软件过程)1.2.2 决…...
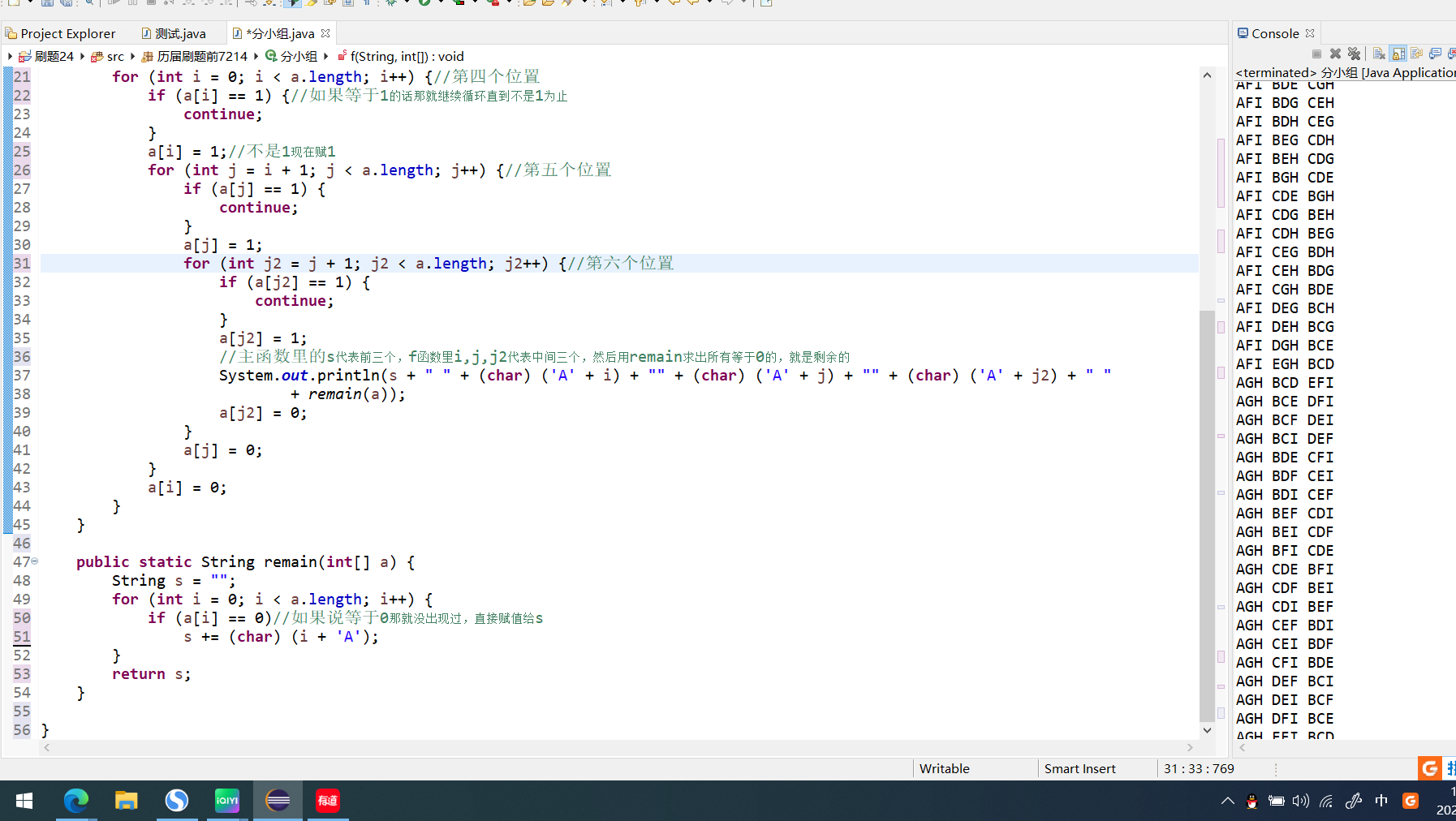
第七届蓝桥杯省赛——5分小组
题目:9名运动员参加比赛,需要分3组进行预赛。有哪些分组的方案呢?我们标记运动员为 A,B,C,... I下面的程序列出了所有的分组方法。该程序的正常输出为:ABC DEF GHIABC DEG FHIABC DEH FGIABC DEI FGHABC DFG EHIABC DFH EGIABC DF…...

中国专科医院行业市场规模及未来发展趋势
中国专科医院行业市场规模及未来发展趋势中国专科医院行业在过去几年中取得了跨越式发展,市场规模不断扩大,未来的发展前景也远比过去更加乐观。根据市场调研在线网发布的2023-2029年中国专科医院行业运营现状及发展前景预测报告分析,截至2018年…...
【刷题笔记】--两数之和Ⅳ,从二叉树中找出两数之和
法一:深度搜索中序遍历双指针 思路:通过中序遍历二叉树得到一个递增的数列,再在这个递增的二叉树中找到这两数。 主要学到双指针这个方法。 对于一般数列,我们要找到两数满足其之和等于目标数,我们一般会进行暴力&a…...

浏览器渲染原理JavaScript V8引擎
浏览器渲染原理 前言 在我们面试过程中,面试官经常会问到这么一个问题,那就是从在浏览器地址栏中输入URL到页面显示,浏览器到底发生了什么? 浏览器内有哪些进程,这些进程都有些什么作用;浏览器地址输入U…...

在TheSandbox 的「BOYS PLANET」元宇宙中与你的男孩们见面吧!
世界各的男孩们成为 K-Pop 男团的旅程。 Mnet 的全球项目 BOYS PLANET 终于在 2 月 2 日首次亮相! The Sandbox 与 CJ ENM 合作,于 2 月 6 日晚上 10 点开始举办两个基于 BOYS PLANET 生存节目的虚拟体验:BOYS PLANET:BOYS LAND 和…...

数据结构与算法:java对象的比较
1.基本类型的比较 在Java中,基本类型的对象可以直接比较大小。 public class TestCompare {public static void main(String[] args) {int a 10;int b 20;System.out.println(a > b);System.out.println(a < b);System.out.println(a b);char c1 A;char…...

python(16)--类
一、类的基本操作1.定义一个类格式:class Classname( ):内容💎鄙人目前还是一名学生,最熟悉的也就是学校了,所以就以学校为例子来建立一个类吧class School():headline"帝国理工大学"def schoolmotto(self):…...
Calico 介绍与原理(二))
CNI 网络流量分析(七)Calico 介绍与原理(二)
文章目录CNI 网络流量分析(七)Calico 介绍与原理(二)CNIIPAM指定 IP指定非 IPAM IPCNI 网络流量分析(七)Calico 介绍与原理(二) CNI 支持多种 datapath,默认是 linuxDa…...

API安全的最大威胁:三体攻击
最近《三体》火的一塌糊涂,动画片、电视剧和书都受到了大家的喜爱。在API安全上,最近也发现了三体攻击。 当然了,肯定是不来自于三体人的攻击,这里的三体攻击指的是(trinity,也称三位一体攻击),是一个新的攻击手法。具体的情况老李也找到了相关的介绍,下面就分享给大…...

分布式事务解决方案——TCC
TCC是Try、Confirm、Cancel三个词语的缩写,TCC要求每个分支事务实现三个操作:预处理Try、确认Confirm、撤销Cancel。1、Try 阶段是做业务检查(一致性)及资源预留(隔离),此阶段仅是一个初步操作,它和后续的Confirm一起才能真正构成…...

ITSS认证分为几个级别,哪个级别最高
一、什么是ITSS ITSS( 信息技术服务标准,简称ITSS)是国内第一套成体系和综合配套的信息技术服务标准库,全面规范了IT服务产品及其组成要素,用于指导实施标准化和可信赖的IT服务。 ITSS是在工业和信息化部、国家标准化管理委员会的联合指导下…...

ZigBee案例笔记 - USART
文章目录1.串行通信接口简述2.串行通信接口寄存器U0CSR (0x86) -USART 0 控制和状态U0UCR (0xC4)–USART 0 UART 控制U0GCR (0xC5)–USART 0 通用控制U0BUF (0xC1) – USART 0 接收/传送数据缓存U0BAUD (0xC2) – USART 0 波特率控制3.设置串行通信接口比特率控制寄存器4.外设I…...

java | 基于Redis的分布式锁实现①
前言 首先,为了确保分布式锁可用,我们至少要确保锁的实现同时满足以下四个条件: 互斥性。在任意时刻,只有一个客户端能持有锁。不会发生死锁。即使有一个客户端在持有锁的期间崩溃而没有主动解锁,也能保证后续其他客户…...

十六、基于FPGA的CRC校验设计实现
1,CRC校验循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种信道编码技术,主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
