17- 梯度提升回归树GBRT (集成算法) (算法)
梯度提升回归树:
- 梯度提升回归树是区别于随机森林的另一种集成方法,它的特点在于纠正与加强,通过合并多个决策树来构建一个更为强大的模型。
- 该模型即可以用于分类问题,也可以用于回归问题中。
- 在该模型中,有三个重要参数分别为 n_estimators(子树数量)、learning_rate(学习率)、max_depth(最大深度)。
- n_estimators 子树数量: 通常用来设置纠正错误的子树数量,梯度提升树通常使用深度很小(1到 5之间)的子树,即强预剪枝,来进行构造强化树。并且这样占用的内存也更少,预测速度也更快。
- learning_rate 学习率: 通常用来控制每颗树纠正前一棵树的强度。较高的学习率意味着每颗树都可以做出较强的修正,这样的模型普遍更复杂。
- max_depth 最大深度: 通常用于降低每颗树的复杂度,从而避免深度过大造成过拟合的现象。梯度提升模型的 max_depth 通常都设置得很小,一般来讲不超过5。
-
梯度提升决策树是监督学习中 最强大也是最常用 的模型之一。
-
该算法无需对数据进行缩放就可以表现得很好,而且也适用于二元特征与连续特征同时存在的数据集。
-
缺点是需要进行仔细调参,且训练时间可能较长,通常不适用于高维稀疏数据。
单一KNN算法: # knn近邻算法: K-近邻算法(KNN)
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(X_train,y_train)
KNN集成算法:
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import BaggingClassifier
# 100个算法,集成算法,准确提升到了73.3%
knn = KNeighborsClassifier()
# bag中100个knn算法
bag_knn = BaggingClassifier(base_estimator=knn, n_estimators=100, max_samples=0.8,max_features=0.7)
bag_knn.fit(X_train,y_train)
print('KNN集成算法,得分是:', bag_knn.score(X_test,y_test))逻辑斯蒂回归集成算法:
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import BaggingClassifier
bag = BaggingClassifier(base_estimator=LogisticRegression(),n_estimators=500,max_samples=0.8, max_features=0.5)
bag.fit(X_train,y_train)决策树集成算法:
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
bag = BaggingClassifier(base_estimator=DecisionTreeClassifier(),n_estimators=100,max_samples=1.0,max_features=0.5)
bag.fit(X_train,y_train)梯度提升回归算法:
from sklearn.ensemble import GradientBoostingRegressor
gbdt = GradientBoostingRegressor(n_estimators=3,loss = 'ls', # 最小二乘法learning_rate=0.1)
gbdt.fit(X,y) # 训练1、集成算法
1.1、不同集成算法
集成算法流程概述
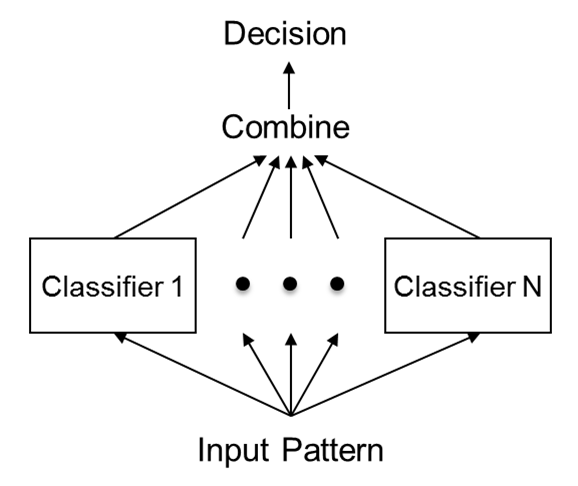
同质学习器(也叫算法,model,模型)
-
随机森林,同质学习器,内部的100个模型,都是决策树
-
bagging:套袋法
-
随机森林
-
极端森林
-
-
boosting:提升法
-
GBDT
-
AdaBoost
-
1.2、bagging
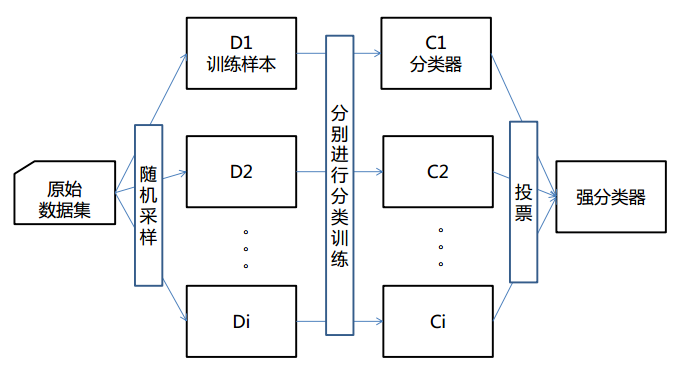
1.3、自建集成算法(同质)
1、导包数据创建
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
X,y = datasets.load_wine(return_X_y = True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 1024)2、KNN集成算法
算法原理:
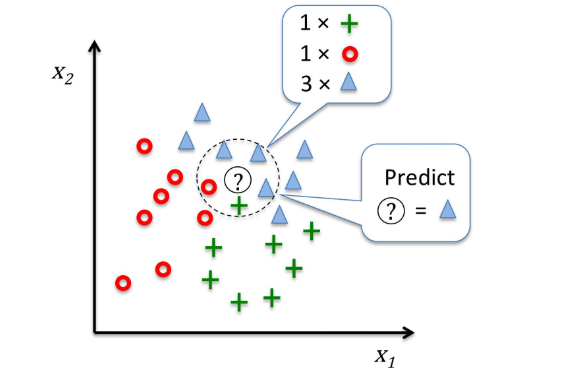
# 一个算法,准确率 62%
knn = KNeighborsClassifier()
knn.fit(X_train,y_train)
print('单一KNN算法,得分是:',knn.score(X_test,y_test)) # 0.6222222222222222# 100个算法,集成算法,准确提升到了73.3%
knn = KNeighborsClassifier()
# bag中100个knn算法
bag_knn = BaggingClassifier(base_estimator=knn,n_estimators=100,max_samples=0.8,max_features=0.7)
bag_knn.fit(X_train,y_train)
print('KNN集成算法,得分是:',bag_knn.score(X_test,y_test)) # 0.7555555555555555 3、逻辑斯蒂回归集成算法
import warnings
warnings.filterwarnings('ignore')
lr = LogisticRegression()
lr.fit(X_train,y_train)
print('单一逻辑斯蒂算法,得分是:',lr.score(X_test,y_test)) # 0.9333333333333333# 偶尔效果会好
bag = BaggingClassifier(base_estimator=LogisticRegression(),n_estimators=500,max_samples=0.8, max_features=0.5)
bag.fit(X_train,y_train)
print('逻辑斯蒂集成算法,得分是:', bag.score(X_test,y_test)) # 0.93333333333333334、决策树自建集成算法
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
print('单棵决策树,得分是:',clf.score(X_test,y_test)) # 0.9555555555555556
bag = BaggingClassifier(base_estimator=DecisionTreeClassifier(),n_estimators=100,max_samples=1.0,max_features=0.5)
bag.fit(X_train,y_train)
print('决策树集成算法,得分是:',bag.score(X_test,y_test)) # 0.97777777777777771.4、boosting
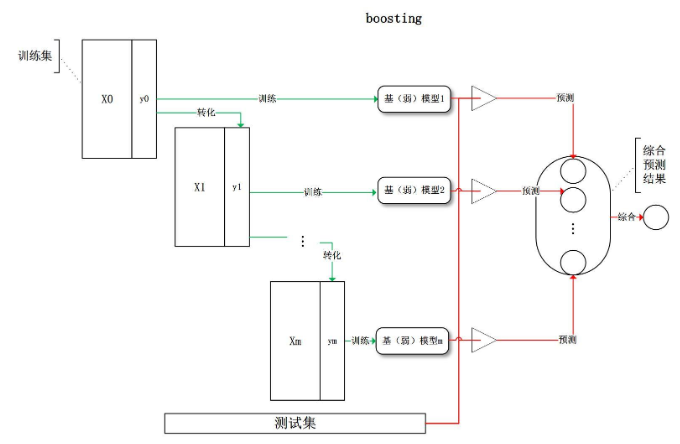
2、GBDT
2.1、梯度提升树概述
-
gradient Boosting DecisionTree 一一> GBDT
-
Boosting :提升的,一点点靠近最优答案
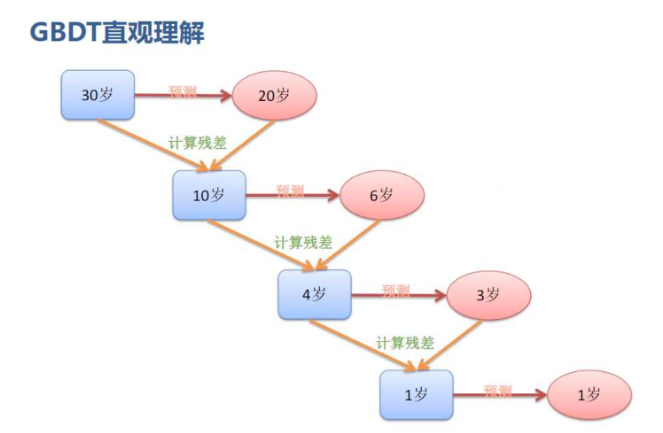
-
残差
-
残差的意思就是: A的预测值 + A的残差 = A的实际值
-
残差 = 实际值 - 预测值
-
预测值 = 实际值 - 残差
-
2.2、梯度提升树应用
1、使用全量数据构建梯度提升树(0.1434)
from sklearn.ensemble import GradientBoostingRegressor
import numpy as np
import pandas as pd # 加载数据
data_train = pd.read_csv('zhengqi_train.txt', sep='\t')
data_test = pd.read_csv('zhengqi_test.txt', sep='\t')
X_train = data_train.iloc[:,:-1]
y_train = data_train['target']
X_test = data_test# GBDT模型训练预测
gbdt = GradientBoostingRegressor()
gbdt.fit(X_train,y_train)
y_pred = gbdt.predict(X_test)
np.savetxt('GBDT_full_feature_result.txt', y_pred)2、使用部分数据构建梯度提升树(0.1486)
from sklearn.linear_model import ElasticNet
from sklearn.ensemble import GradientBoostingRegressor
import numpy as np
import pandas as pd # 加载数据
data_train = pd.read_csv('zhengqi_train.txt', sep='\t')
data_test = pd.read_csv('zhengqi_test.txt', sep='\t')
X_train = data_train.iloc[:,:-1]
y_train = data_train['target']
X_test = data_test# 先使用ElaticNet模型进行数据筛选
model = ElasticNet(alpha = 0.1, l1_ratio=0.05)
model.fit(X_train, y_train)
cond = model.coef_ != 0
X_train = X_train.iloc[:,cond]
X_test = X_test.iloc[:,cond]
print('删除数据后,形状是:',X_train.shape)# GBDT模型训练预测
gbdt = GradientBoostingRegressor()
gbdt.fit(X_train,y_train)
y_pred = gbdt.predict(X_test)
np.savetxt('GBDT_drop_feature_result.txt', y_pred)2.3、梯度提升树原理
1、创建数据并使用梯度提升回归树进行预测
import numpy as np
from sklearn.ensemble import GradientBoostingRegressor
import matplotlib.pyplot as plt
from sklearn import tree
import graphviz### 实际问题,年龄预测,回归问题
# 简单的数据,算法原理,无论简单数据,还是复杂数据,都一样
# 属性一表示花销,属性二表示上网时间
X = np.array([[600,0.8],[800,1.2],[1500,10],[2500,3]])
y = np.array([14,16,24,26]) # 高一、高三,大四,工作两年
# loss = ls 最小二乘法
learning_rate = 0.1
gbdt = GradientBoostingRegressor(n_estimators=3,loss = 'ls',# 最小二乘法learning_rate=0.1)#learning_rate 学习率
gbdt.fit(X,y)#训练
y_ = gbdt.predict(X) # 预测2、计算残差
# 目标值,真实值,算法,希望,预测,越接近真实,模型越好!!!
print(y)
# 求平均,这个平均值就是算法第一次预测的基准,初始值
print(y.mean())
# 残差:真实值,和预测值之间的差
residual = y - y.mean()
residual
# 残差,越小越好
# 如果残差是0,算法完全准确的把数值预测出来!3、绘制三棵树
-
第一棵树
# 第一颗树,分叉时,friedman-mse (就是均方误差)= 26
print('均方误差:',((y - y.mean())**2).mean())
dot_data = tree.export_graphviz(gbdt[0,0],filled=True)
graph = graphviz.Source(dot_data)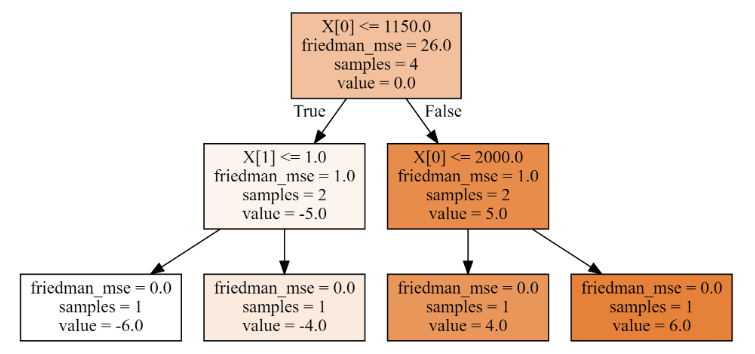
# 梯度下降,降低残差
residual = residual - learning_rate*residual
residual
# 输出:array([-5.4, -3.6, 3.6, 5.4])- 第二棵树
# 第二颗树
dot_data = tree.export_graphviz(gbdt[1,0],filled=True)
graph = graphviz.Source(dot_data)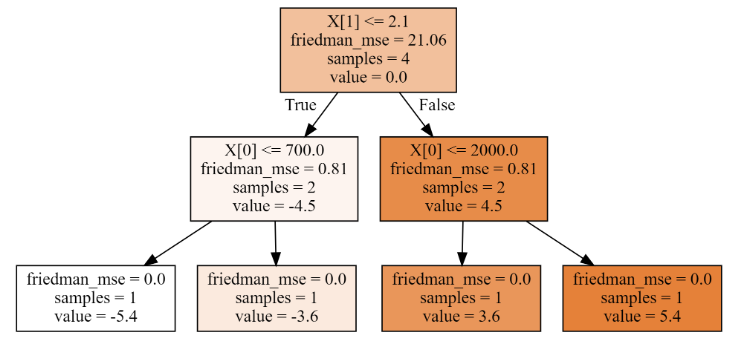
# 梯度下降,降低残差
residual = residual - learning_rate*residual
residual
# 输出:array([-4.86, -3.24, 3.24, 4.86])- 第三棵树
# 第三颗树
dot_data = tree.export_graphviz(gbdt[2,0],filled=True)
graph = graphviz.Source(dot_data)# 梯度下降,降低残差
residual = residual - learning_rate*residual
residual
# 输出:array([-4.374, -2.916, 2.916, 4.374])4、使用残差计算最终结果
# 使用残差一步步,计算的结果
y_ = y - residual
print('使用残差一步步计算,最终结果是:\n',y_)
# 使用算法,预测
gbdt.predict(X)
# 两者输出结果一样2.4、梯度提升回归树的最佳裂分条件计算
1、第一棵树,分裂情况如下:
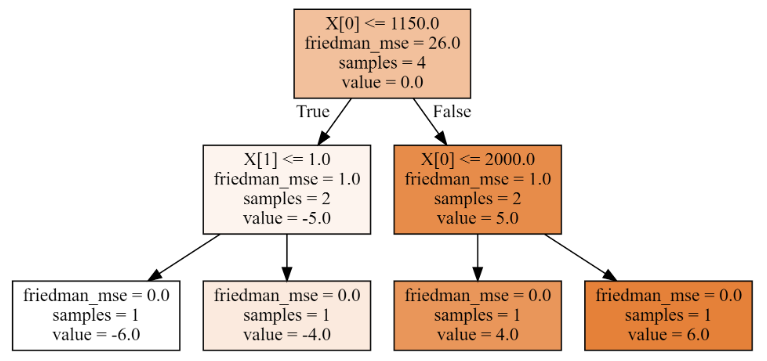
# 计算未分裂均方误差
lower_mse = ((y - y.mean())**2).mean()
print('未分裂均方误差是:',lower_mse)
best_split = {}
for index in range(2):for i in range(3):t = X[:,index].copy()t.sort()split = t[i:i + 2].mean()cond = X[:,index] <= splitmse1 = round(((y[cond] - y[cond].mean())**2).mean(),3)mse2 = round(((y[~cond] - y[~cond].mean())**2).mean(),3)p1 = cond.sum()/cond.sizemse = round(mse1 * p1 + mse2 * (1- p1),3)print('第%d列' % (index),'裂分条件是:',split,'均方误差是:',mse1,mse2,mse)if mse < lower_mse:best_split.clear()lower_mse = msebest_split['第%d列'%(index)] = splitelif mse == lower_mse:best_split['第%d列'%(index)] = split
print('最佳分裂条件是:',best_split)
# 输出:
'''
未分裂均方误差是: 26.0
第0列 裂分条件是: 700.0 均方误差是: 0.0 18.667 14.0
第0列 裂分条件是: 1150.0 均方误差是: 1.0 1.0 1.0
第0列 裂分条件是: 2000.0 均方误差是: 18.667 0.0 14.0
第1列 裂分条件是: 1.0 均方误差是: 0.0 18.667 14.0
第1列 裂分条件是: 2.1 均方误差是: 1.0 1.0 1.0
第1列 裂分条件是: 6.5 均方误差是: 27.556 0.0 20.667
最佳分裂条件是: {'第0列': 1150.0, '第1列': 2.1}
'''2、第二棵树,分裂情况如下:
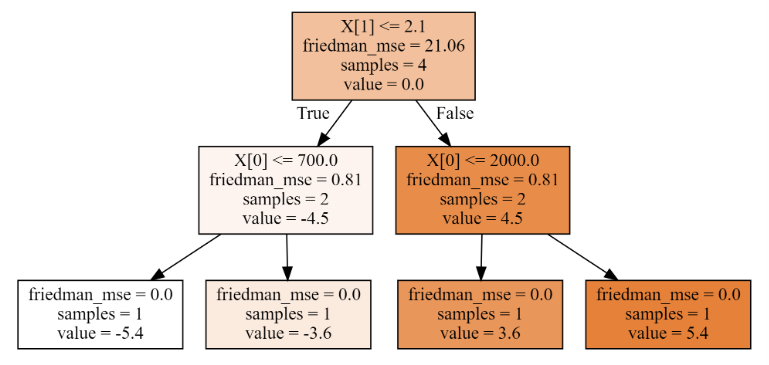
# 梯度下降,降低残差
residual = residual - learning_rate*residual
# 计算未分裂均方误差
lower_mse = round(((residual - residual.mean())**2).mean(),3)
print('未分裂均方误差是:',lower_mse)
best_split = {}
for index in range(2):for i in range(3):t = X[:,index].copy()t.sort()split = t[i:i + 2].mean()cond = X[:,index] <= splitmse1 = round(((residual[cond] - residual[cond].mean())**2).mean(),3)mse2 = round(((residual[~cond] - residual[~cond].mean())**2).mean(),3)p1 = cond.sum()/cond.sizemse = round(mse1 * p1 + mse2 * (1- p1),3)print('第%d列' % (index),'裂分条件是:',split,'均方误差是:',mse1,mse2,mse)if mse < lower_mse:best_split.clear()lower_mse = msebest_split['第%d列'%(index)] = splitelif mse == lower_mse:best_split['第%d列'%(index)] = split
print('最佳分裂条件是:',best_split)
# 输出
'''
未分裂均方误差是: 21.06
第0列 裂分条件是: 700.0 均方误差是: 0.0 15.12 11.34
第0列 裂分条件是: 1150.0 均方误差是: 0.81 0.81 0.81
第0列 裂分条件是: 2000.0 均方误差是: 15.12 0.0 11.34
第1列 裂分条件是: 1.0 均方误差是: 0.0 15.12 11.34
第1列 裂分条件是: 2.1 均方误差是: 0.81 0.81 0.81
第1列 裂分条件是: 6.5 均方误差是: 22.32 0.0 16.74
最佳分裂条件是: {'第0列': 1150.0, '第1列': 2.1}
'''3、第三棵树,分裂情况如下:
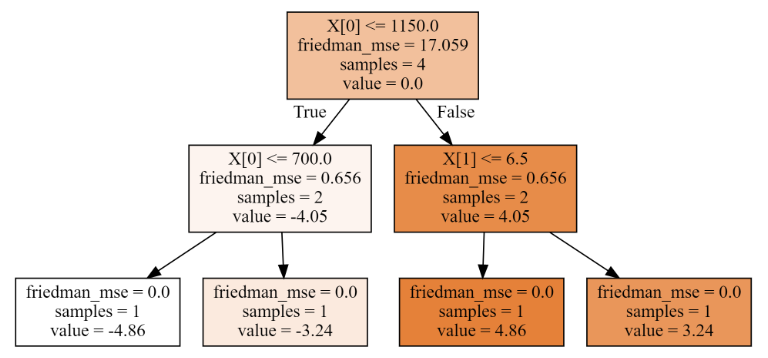
# 梯度下降,降低残差
residual = residual - learning_rate*residual
# 计算未分裂均方误差
lower_mse = round(((residual - residual.mean())**2).mean(),3)
print('未分裂均方误差是:',lower_mse)
best_split = {}
for index in range(2):for i in range(3):t = X[:,index].copy()t.sort()split = t[i:i + 2].mean()cond = X[:,index] <= splitmse1 = round(((residual[cond] - residual[cond].mean())**2).mean(),3)mse2 = round(((residual[~cond] - residual[~cond].mean())**2).mean(),3)p1 = cond.sum()/cond.sizemse = round(mse1 * p1 + mse2 * (1- p1),3)print('第%d列' % (index),'裂分条件是:',split,'均方误差是:',mse1,mse2,mse)if mse < lower_mse:best_split.clear()lower_mse = msebest_split['第%d列'%(index)] = splitelif mse == lower_mse:best_split['第%d列'%(index)] = split
print('最佳分裂条件是:',best_split)
# 输出
'''
未分裂均方误差是: 17.059
第0列 裂分条件是: 700.0 均方误差是: 0.0 12.247 9.185
第0列 裂分条件是: 1150.0 均方误差是: 0.656 0.656 0.656
第0列 裂分条件是: 2000.0 均方误差是: 12.247 0.0 9.185
第1列 裂分条件是: 1.0 均方误差是: 0.0 12.247 9.185
第1列 裂分条件是: 2.1 均方误差是: 0.656 0.656 0.656
第1列 裂分条件是: 6.5 均方误差是: 18.079 0.0 13.559
最佳分裂条件是: {'第0列': 1150.0, '第1列': 2.1}
'''相关文章:

17- 梯度提升回归树GBRT (集成算法) (算法)
梯度提升回归树: 梯度提升回归树是区别于随机森林的另一种集成方法,它的特点在于纠正与加强,通过合并多个决策树来构建一个更为强大的模型。该模型即可以用于分类问题,也可以用于回归问题中。在该模型中,有三个重要参数分别为 n_…...

05 OpenCV色彩空间处理
色彩空间(Color Space)是一种用于描述颜色的数学模型,它将颜色表示为多维向量或坐标,通常由三个或四个独立的分量来表示。不同的色彩空间在颜色的表示方式、可表达颜色的范围、计算速度和应用场景等方面存在差异,不同的…...
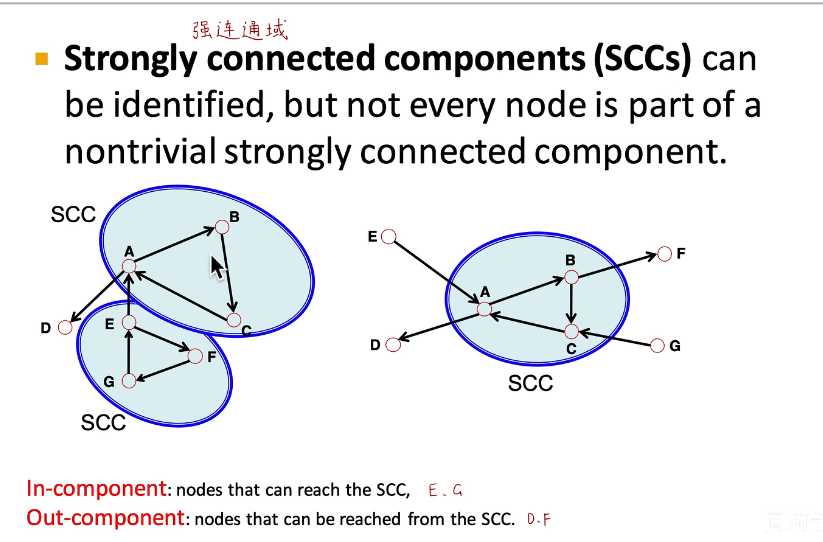
【CS224图机器学习】task1 图机器学习导论
前言:本期学习是由datawhale(公众号)组织,由子豪兄讲解的202302期CS224图机器学习的学习笔记。本次学习主要针对图机器学习导论做学习总结。1.什么是图机器学习?通过图这种数据结构,对跨模态数据进行整理。…...
Powershell Install SQL Server 2022
前言 SQL Server 2022 (16.x) 在早期版本的基础上构建,旨在将 SQL Server 发展成一个平台,以提供开发语言、数据类型、本地或云环境以及操作系统选项。 SQL Server Management Studio (SSMS) 是一种集成环境,用于管理从 SQL Server 到 Azure SQL 数据库的任何 SQL 基础结构…...

Jetson NX2 装机过程
1.固态硬盘安装完成后,系统配置 df -h 查看硬盘使用情况 2.查看Jetson NX的IP地址,以下两个都行 ifconfig ip address show 3.Jetson NX2安装arm64的annaconda3,安装有问题报错illegal instruction,未解决。 4.VNC远程登录 …...

初始C++(四):内联函数
文章目录一.内联函数概念二.内联函数用法三.内联函数的特性四.内联函数和宏一.内联函数概念 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调用建立栈帧的开销,内联函数提升程序运行的效率。 二.内联函…...

九、初识卷积
文章目录1、通过边缘检测认识卷积2、Padding3、Strid Convelution4、RGB图像的卷积THE END1、通过边缘检测认识卷积 \qquad在使用神经网络进行图像识别时,神经网络的前几层需要完成对图像的边缘检测任务,所谓的边缘检测就是让计算机识别出一张图片的垂直…...

【Linux】【编译】编译调试过程中如何打印出实际的编译命令
🐚作者简介:花神庙码农(专注于Linux、WLAN、TCP/IP、Python等技术方向)🐳博客主页:花神庙码农 ,地址:https://blog.csdn.net/qxhgd🌐系列专栏:Linux技术&…...

linux安装jdk
step1 下载jdk 到下面的网站下载需要的jdk安装包版本。 Java Downloads | Oracle step2 复制到opt目录 其中user_name对应自己的home目录的用户文件夹 sudo cp /home/user_name//home/czh/Downloads/jdk-17_linux-x64_bin.tar.gz /opt/ step3 到opt目录解压安装包…...

迅为iTOP-3A5000龙芯开发板安装UOS操作系统
3A5000板卡采用全国产龙芯3A5000处理器,基于龙芯自主指令系统(LoongArch),市面上龙芯3A5000主板价格都在上万元,可以说是非常贵了, 迅为全新推出了款千元内的iTOP-3A5000开发板,这款板卡各方面的配置也是第…...

Firefox 110, Chrome 110, Chromium 110 官网离线下载 (macOS, Linux, Windows)
Mozilla Firefox, Google Chrome, Chromium, Apple Safari 请访问原文链接:https://sysin.org/blog/chrome-firefox-download/,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org 天下只剩三种(主流&am…...
如何使用ArcGIS转换坐标
1.概述大家都知道ArcGIS提供了坐标转换功能,在我们手里的数据坐标系千差万别,经常会遇到转换坐标的时候,那么是否可以用ArcGIS进行转换?答案是肯定的,但是转换的过程比较复杂,这里为大家介绍一下转换的方法…...

链表基本原理
链表基本原理1.链表1.1 基本原理1.2 链表大O记法表示2. 链表操作2.1 读取2.2 查找2.3 插入2.4 删除3.链表代码实现1.链表 1.1 基本原理 节点 组成链表的数据格子不是连续的。可以分布在内存的各个位置。这种不相邻的格子就叫结点。每个结点保存数据还保存着链表里的下一结点的…...

基于JAVA+SpringBoot+Vue+ElementUI中学化学实验室耗材管理系统
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 当前,中学…...

1.输入子系统学习-struct input_dev-2023.02
内核版本:4.4.194 平台相关:rk3399 目前主要是看的触摸屏的代码 目录 一、include/linux/input.h(struct_input_dev) 二、结构体的注释部分(百度翻译) 三、Documentation/input/event-codes.txt&…...

解决:PDFBox报的java.io.IOException: Missing root object specification in trailer
文章目录问题描述原因分析解决方案问题描述 使用pdfbox类库操作pdf文件时,遇到下面的报错信息: java.io.IOException: Missing root object specification in trailer PDFBox参考: https://pdfbox.apache.org/ Apache PDFBox 库是一个开源的…...

MAC OSX安装Python环境 + Visual Studio Code
MAC上开发python怎么能少得了python3环境呢,而安装python3环境的方式也有多种,这里仅选用并记录本人认为比较方便的方式 安装Homebrew Homebrew是macOS 缺失的软件包管理器, 使用它可以在MAC上安装很多没有预装的东西,详细说明可…...
音乐 APP 用户争夺战,火山引擎 VeDI 助力用户体验升级!
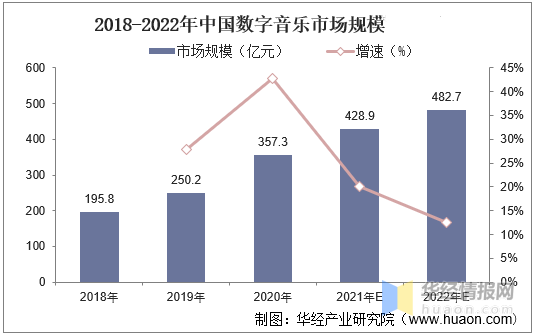
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,并进入官方交流群 国内数字音乐市场正在保持稳定增长。 根据华经产业研究院数据报告显示,2020 年数字音乐市场规模为 357.3 亿元,到 2022 年市场规模已增长至 482.7 …...

CAP和BASE理论
CAP理论CAP是 Consistency、Availability、Partition tolerance 三个词语的缩写,分别表示一致性、可用性、分区容忍性。它指出一个分布式计算系统不可能同时满足以下三点:• 一致性(Consistency) :等同于所有节点访问同…...

基于商品理解的成交能力和成交满意度优化在Lazada的实践
作者:马蕊 Lazada推荐算法团队 在Lazada各域推荐场景中,既有优质商品优质卖家不断涌现带来的机会,也有商品质量参差带来的问题。如何才能为用户提供更好的体验,对卖家变化行为进行正向激励呢?下面本文将为大家分享我们…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
