算法思想 - 搜索算法
本文主要介绍算法中搜索算法的思想,主要包含BFS,DFS。
搜索相关题目
深度优先搜索和广度优先搜索广泛运用于树和图中,但是它们的应用远远不止如此。
BFS
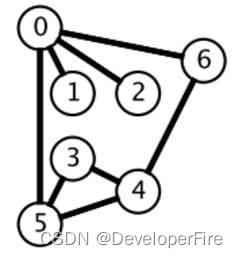
广度优先搜索的搜索过程有点像一层一层地进行遍历,每层遍历都以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历。
第一层:
0 -> {6,2,1,5};
第二层:
6 ->
2 -> {}
1 -> {}
5 ->
第三层:
4 -> {}
3 -> {}
可以看到,每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离,推导出一个结论: 对于先遍历的节点 i 与后遍历的节点 j,有 di<=dj。利用这个结论,可以求解最短路径等 最优解 问题: 第一次遍历到目的节点,其所经过的路径为最短路径。应该注意的是,使用 BFS 只能求解无权图的最短路径。
在程序实现 BFS 时需要考虑以下问题:
队列: 用来存储每一轮遍历得到的节点;
标记: 对于遍历过的节点,应该将它标记,防止重复遍历。
计算在网格中从原点到特定点的最短路径长度
[[1,1,0,1],[1,0,1,0],[1,1,1,1],[1,0,1,1]]1 表示可以经过某个位置,求解从 (0, 0) 位置到 (tr, tc) 位置的最短路径长度。
public int minPathLength(int[][] grids, int tr, int tc) {final int[][] direction = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};final int m = grids.length, n = grids[0].length;Queue<Pair<Integer, Integer>> queue = new LinkedList<>();queue.add(new Pair<>(0, 0));int pathLength = 0;while (!queue.isEmpty()) {int size = queue.size();pathLength++;while (size-- > 0) {Pair<Integer, Integer> cur = queue.poll();for (int[] d : direction) {int nr = cur.getKey() + d[0], nc = cur.getValue() + d[1];Pair<Integer, Integer> next = new Pair<>(nr, nc);if (next.getKey() < 0 || next.getValue() >= m|| next.getKey() < 0 || next.getValue() >= n) {continue;}grids[next.getKey()][next.getValue()] = 0; // 标记if (next.getKey() == tr && next.getValue() == tc) {return pathLength;}queue.add(next);}}}return -1;
}组成整数的最小平方数数量
279. Perfect Squares (Medium)
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.可以将每个整数看成图中的一个节点,如果两个整数之差为一个平方数,那么这两个整数所在的节点就有一条边。
要求解最小的平方数数量,就是求解从节点 n 到节点 0 的最短路径。
本题也可以用动态规划求解,在之后动态规划部分中会再次出现。
public int numSquares(int n) {List<Integer> squares = generateSquares(n);Queue<Integer> queue = new LinkedList<>();boolean[] marked = new boolean[n + 1];queue.add(n);marked[n] = true;int level = 0;while (!queue.isEmpty()) {int size = queue.size();level++;while (size-- > 0) {int cur = queue.poll();for (int s : squares) {int next = cur - s;if (next < 0) {break;}if (next == 0) {return level;}if (marked[next]) {continue;}marked[next] = true;queue.add(cur - s);}}}return n;
}/*** 生成小于 n 的平方数序列* @return 1,4,9,...*/
private List<Integer> generateSquares(int n) {List<Integer> squares = new ArrayList<>();int square = 1;int diff = 3;while (square <= n) {squares.add(square);square += diff;diff += 2;}return squares;
}最短单词路径
127. Word Ladder (Medium)
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]Output: 5Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]Output: 0Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.找出一条从 beginWord 到 endWord 的最短路径,每次移动规定为改变一个字符,并且改变之后的字符串必须在 wordList 中。
public int ladderLength(String beginWord, String endWord, List<String> wordList) {wordList.add(beginWord);int N = wordList.size();int start = N - 1;int end = 0;while (end < N && !wordList.get(end).equals(endWord)) {end++;}if (end == N) {return 0;}List<Integer>[] graphic = buildGraphic(wordList);return getShortestPath(graphic, start, end);
}private List<Integer>[] buildGraphic(List<String> wordList) {int N = wordList.size();List<Integer>[] graphic = new List[N];for (int i = 0; i < N; i++) {graphic[i] = new ArrayList<>();for (int j = 0; j < N; j++) {if (isConnect(wordList.get(i), wordList.get(j))) {graphic[i].add(j);}}}return graphic;
}private boolean isConnect(String s1, String s2) {int diffCnt = 0;for (int i = 0; i < s1.length() && diffCnt <= 1; i++) {if (s1.charAt(i) != s2.charAt(i)) {diffCnt++;}}return diffCnt == 1;
}private int getShortestPath(List<Integer>[] graphic, int start, int end) {Queue<Integer> queue = new LinkedList<>();boolean[] marked = new boolean[graphic.length];queue.add(start);marked[start] = true;int path = 1;while (!queue.isEmpty()) {int size = queue.size();path++;while (size-- > 0) {int cur = queue.poll();for (int next : graphic[cur]) {if (next == end) {return path;}if (marked[next]) {continue;}marked[next] = true;queue.add(next);}}}return 0;
}DFS
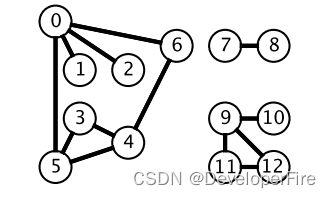
广度优先搜索一层一层遍历,每一层得到的所有新节点,要用队列存储起来以备下一层遍历的时候再遍历。
而深度优先搜索在得到一个新节点时立马对新节点进行遍历: 从节点 0 出发开始遍历,得到到新节点 6 时,立马对新节点 6 进行遍历,得到新节点 4;如此反复以这种方式遍历新节点,直到没有新节点了,此时返回。返回到根节点 0 的情况是,继续对根节点 0 进行遍历,得到新节点 2,然后继续以上步骤。
从一个节点出发,使用 DFS 对一个图进行遍历时,能够遍历到的节点都是从初始节点可达的,DFS 常用来求解这种 可达性 问题。
在程序实现 DFS 时需要考虑以下问题:
栈: 用栈来保存当前节点信息,当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
标记: 和 BFS 一样同样需要对已经遍历过的节点进行标记。
查找最大的连通面积
695. Max Area of Island (Easy)
[[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int maxAreaOfIsland(int[][] grid) {if (grid == null || grid.length == 0) {return 0;}m = grid.length;n = grid[0].length;int maxArea = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {maxArea = Math.max(maxArea, dfs(grid, i, j));}}return maxArea;
}private int dfs(int[][] grid, int r, int c) {if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0) {return 0;}grid[r][c] = 0;int area = 1;for (int[] d : direction) {area += dfs(grid, r + d[0], c + d[1]);}return area;
}矩阵中的连通分量数目
200. Number of Islands (Medium)
Input:
11000
11000
00100
00011Output: 3可以将矩阵表示看成一张有向图。
private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int numIslands(char[][] grid) {if (grid == null || grid.length == 0) {return 0;}m = grid.length;n = grid[0].length;int islandsNum = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] != '0') {dfs(grid, i, j);islandsNum++;}}}return islandsNum;
}private void dfs(char[][] grid, int i, int j) {if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') {return;}grid[i][j] = '0';for (int[] d : direction) {dfs(grid, i + d[0], j + d[1]);}
}好友关系的连通分量数目
547. Friend Circles (Medium)
Input:
[[1,1,0],[1,1,0],[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.好友关系可以看成是一个无向图,例如第 0 个人与第 1 个人是好友,那么 M[0][1] 和 M[1][0] 的值都为 1。
private int n;public int findCircleNum(int[][] M) {n = M.length;int circleNum = 0;boolean[] hasVisited = new boolean[n];for (int i = 0; i < n; i++) {if (!hasVisited[i]) {dfs(M, i, hasVisited);circleNum++;}}return circleNum;
}private void dfs(int[][] M, int i, boolean[] hasVisited) {hasVisited[i] = true;for (int k = 0; k < n; k++) {if (M[i][k] == 1 && !hasVisited[k]) {dfs(M, k, hasVisited);}}
}填充封闭区域
130. Surrounded Regions (Medium)
For example,
X X X X
X O O X
X X O X
X O X XAfter running your function, the board should be:
X X X X
X X X X
X X X X
X O X X使被 'X' 包围的 'O' 转换为 'X'。
先填充最外侧,剩下的就是里侧了。
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
private int m, n;public void solve(char[][] board) {if (board == null || board.length == 0) {return;}m = board.length;n = board[0].length;for (int i = 0; i < m; i++) {dfs(board, i, 0);dfs(board, i, n - 1);}for (int i = 0; i < n; i++) {dfs(board, 0, i);dfs(board, m - 1, i);}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (board[i][j] == 'T') {board[i][j] = 'O';} else if (board[i][j] == 'O') {board[i][j] = 'X';}}}
}private void dfs(char[][] board, int r, int c) {if (r < 0 || r >= m || c < 0 || c >= n || board[r][c] != 'O') {return;}board[r][c] = 'T';for (int[] d : direction) {dfs(board, r + d[0], c + d[1]);}
}能到达的太平洋和大西洋的区域
417. Pacific Atlantic Water Flow (Medium)
Given the following 5x5 matrix:Pacific ~ ~ ~ ~ ~~ 1 2 2 3 (5) *~ 3 2 3 (4) (4) *~ 2 4 (5) 3 1 *~ (6) (7) 1 4 5 *~ (5) 1 1 2 4 ** * * * * AtlanticReturn:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (positions with parentheses in above matrix).左边和上边是太平洋,右边和下边是大西洋,内部的数字代表海拔,海拔高的地方的水能够流到低的地方,求解水能够流到太平洋和大西洋的所有位置。
private int m, n;
private int[][] matrix;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public List<int[]> pacificAtlantic(int[][] matrix) {List<int[]> ret = new ArrayList<>();if (matrix == null || matrix.length == 0) {return ret;}m = matrix.length;n = matrix[0].length;this.matrix = matrix;boolean[][] canReachP = new boolean[m][n];boolean[][] canReachA = new boolean[m][n];for (int i = 0; i < m; i++) {dfs(i, 0, canReachP);dfs(i, n - 1, canReachA);}for (int i = 0; i < n; i++) {dfs(0, i, canReachP);dfs(m - 1, i, canReachA);}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (canReachP[i][j] && canReachA[i][j]) {ret.add(new int[]{i, j});}}}return ret;
}private void dfs(int r, int c, boolean[][] canReach) {if (canReach[r][c]) {return;}canReach[r][c] = true;for (int[] d : direction) {int nextR = d[0] + r;int nextC = d[1] + c;if (nextR < 0 || nextR >= m || nextC < 0 || nextC >= n|| matrix[r][c] > matrix[nextR][nextC]) {continue;}dfs(nextR, nextC, canReach);}
}相关文章:

算法思想 - 搜索算法
本文主要介绍算法中搜索算法的思想,主要包含BFS,DFS。搜索相关题目深度优先搜索和广度优先搜索广泛运用于树和图中,但是它们的应用远远不止如此。BFS广度优先搜索的搜索过程有点像一层一层地进行遍历,每层遍历都以上一层遍历的结果…...
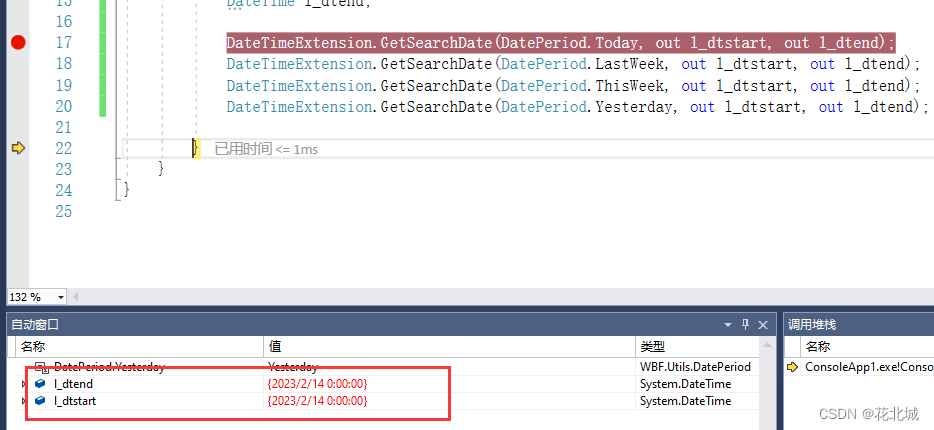
C#底层库--日期扩展类(上周、本周、明年、前年等)
系列文章 C#底层库–记录日志帮助类 本文链接:https://blog.csdn.net/youcheng_ge/article/details/124187709 C#底层库–数据库访问帮助类(MySQL版) 本文链接:https://blog.csdn.net/youcheng_ge/article/details/126886379 …...

如何在 Webpack 中开启图片压缩
工具对比 npmtrends.com/image-minim… 这四个压缩工具,从下载量来看,image-webpack-loader 较多,image-minimizer-webpack-plugin、imagemin-webpack-plugin 次之,imagemin-webpack 已经不再维护,因此不考虑此工具。 …...

Web-Filter
## 今日内容 1. Filter:过滤器 2. Listener:监听器 # Filter:过滤器 1. 概念: * 生活中的过滤器:净水器,空气净化器,土匪、 * web中的过滤器:当访问服务器的资源时…...

测试写文章自动保存
近日恰逢双十一,瞅了瞅自己干瘪的钱包,没忍心入手期待已久的 macPro,只好在虚拟机里玩一下 mac好了,等以后钱包傲气的时候再来个真实的。 安装环境: windows10 VMWare14.2 2018-7-28 小嘚瑟补充:唧唧歪歪大半年,一夜回到解放前,终于剁手整了个真机,可以折腾一下了 ——…...

云平台搭建实例
嗨嗨,每天一更是不是很奈斯?我也觉得,昨天晚上我学校的老师借一天一千的设备,只能用七天,所以我拿出来给你们没有设备和刚用设备的看看吧。操作:首先我们将云平台安装好后,插上网线,…...

【Airplay_BCT】关于Bonjour的概念解答
1.什么是Bonjour? Bonjour,也称为零配置网络,可以自动发现 IP 网络上的计算机、设备和服务。 Bonjour 使用行业标准 IP 协议,允许设备自动发现彼此,无需输入 IP 地址或配置 DNS 服务器。具体来说,Bonjour …...
C++深入浅出(九)—— 多态
文章目录1. 多态的概念2. 多态的定义及实现🍑 多态的构成条件🍑 虚函数🍑 虚函数的重写🍑 虚函数重写的两个例外🍑 C11的override 和 final🍑 重载、覆盖(重写)、隐藏(重定义)的对比3. 抽象类🍑…...
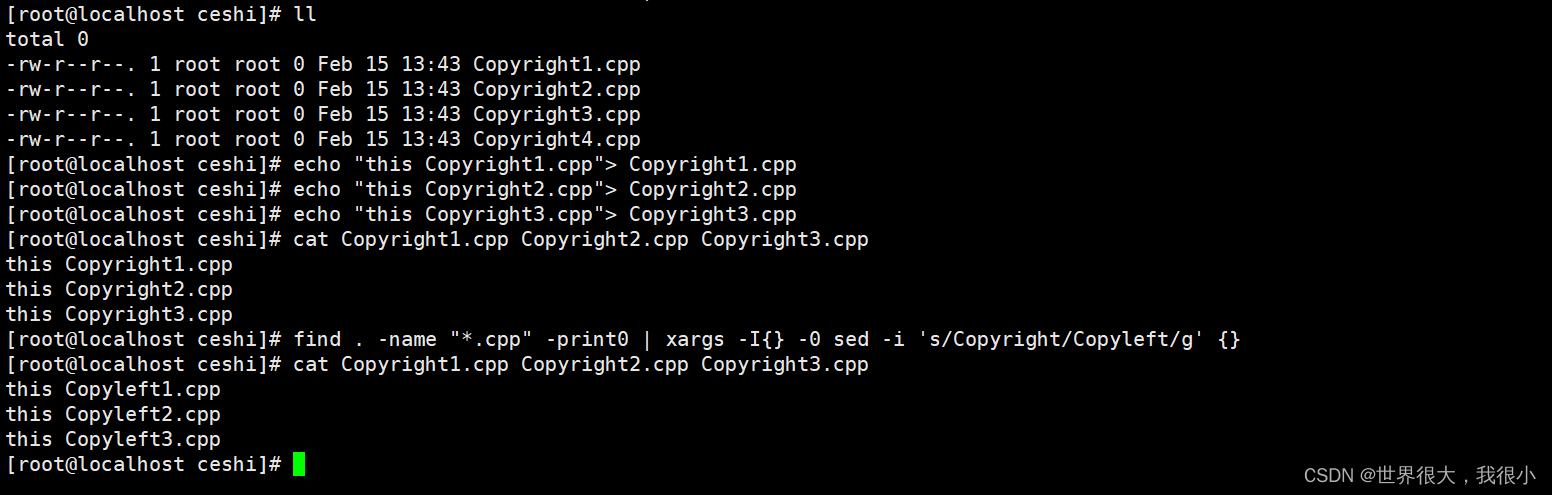
shell学习4
目录 一、统计文本中的词频 二、压缩javascript 三、打印文件的或行中的第n个单词或列---awk 3.1 利用awk打印文件中每行中的第五个单词。 3.2 利用awk打印当前目录下的文件的权限和文件名 3.3 利用awk打印从M行到N行这个范围内的所有文本 3.4 利用awk 部分提取文件中的内…...

VR全景行业的应用价值如何呈现?
互联网高速发展的今天,多媒体所包含的种类也是越来越多,而一些较为传统的表现方式已经越来越无法满足大部分客户对展示方式的要求。而在传统的表现方式中,展现的方式无非是静态的平面图片以及动态的视频,但是他们都有一个缺点就是…...
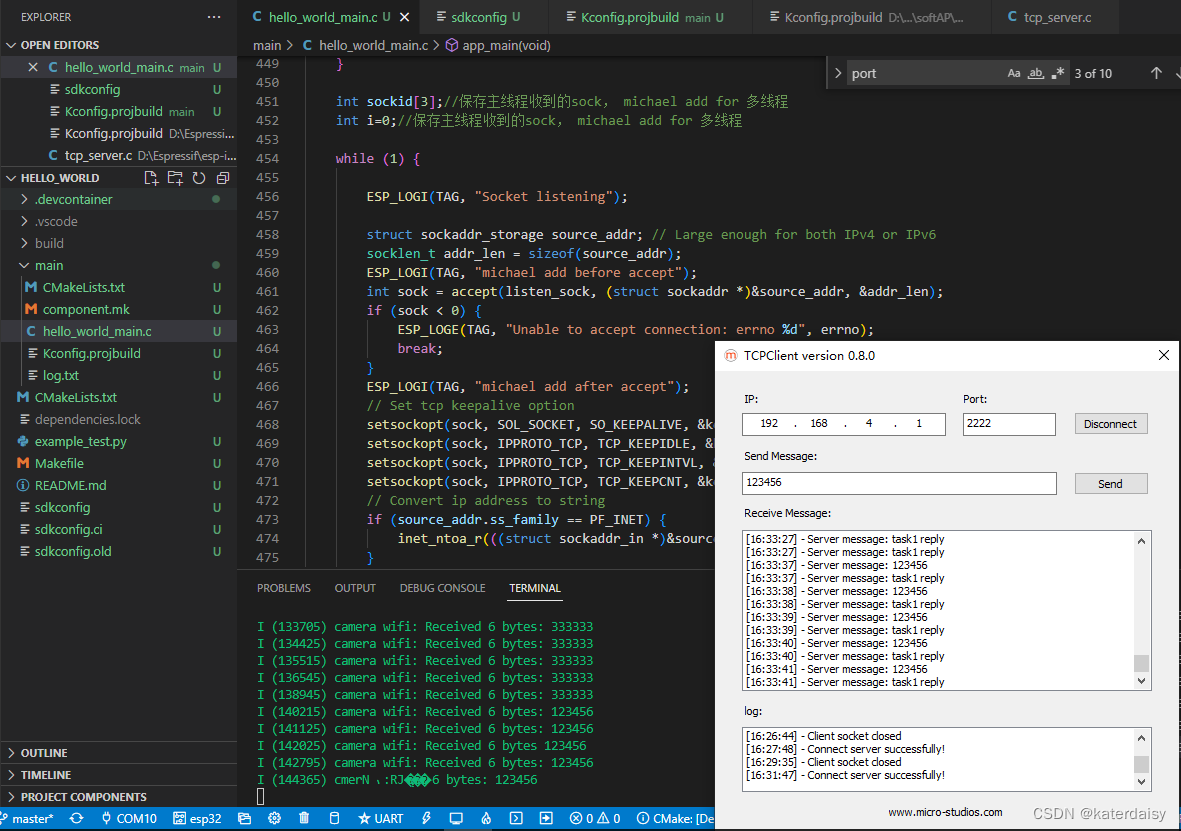
ESP-IDF:TCP多线程并发服务器
核心代码: 核心思想就是主线程只处理socket监听功能,把数据处理部分分配到不同的线程中去处理。来了一个客户端连接,就分配新的线程去处理该客户端的数据请求。 代码: /多线程并发服务器/ #include <stdio.h> #include …...
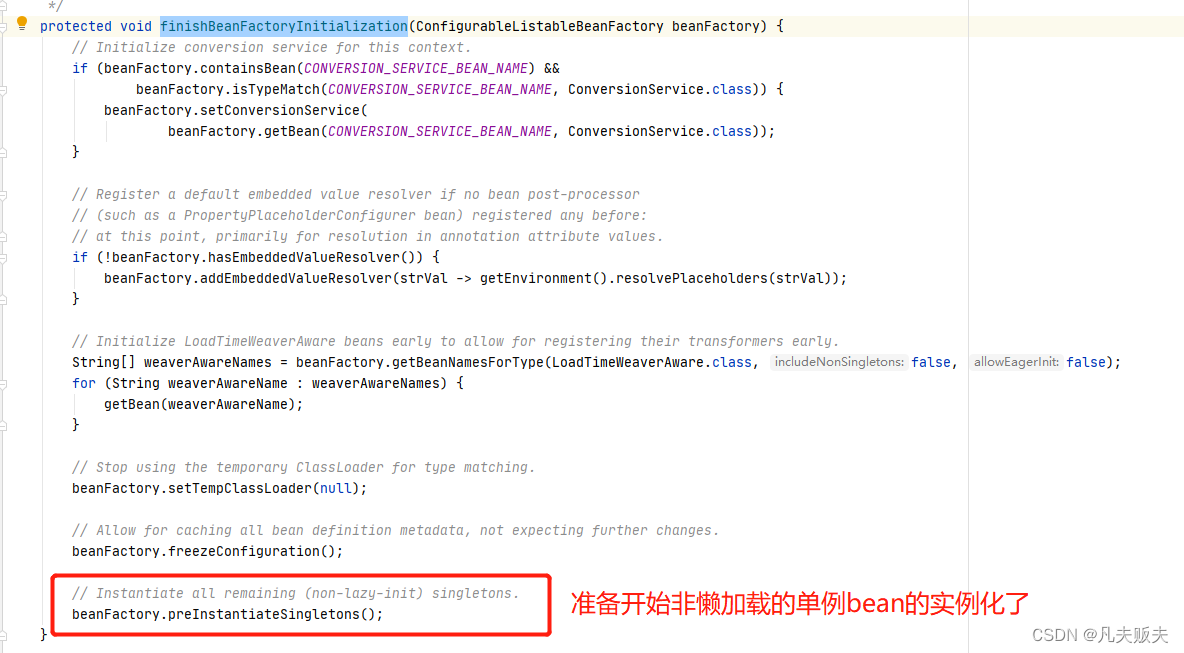
Springboot扩展点之SmartInitializingSingleton
前言这篇文章会重点分析一下SmartInitializingSingleton扩展点的功能 特性、实现方式 、工作原理。SmartInitializingSingleton扩展点内只有一个扩展方法,且执行时机在Spring Bean的生命周期里比较靠后,很重要,但是也很简单。功能特性1、Smar…...

基于linux内核的驱动开发学习
1 驱动 定义:驱使硬件动起来的程序 种类:裸机驱动:需求分析--》查原理图--》查芯片手册--》code 系统驱动:需求分析--》查原理图--》查芯片手册--》设备树--》code --》安装到内核中…...

python3 django gunicorn
首先,Gunicorn是一个高效的Web服务器,地位相当于Java中的Tomcat。简单来说gunicorn封装了HTTP的底层实现,我们通过gunicorn启动服务,用户请求与服务相应都经过gunicorn传输。下载gunicorn的方法也比较简单,在django工程…...
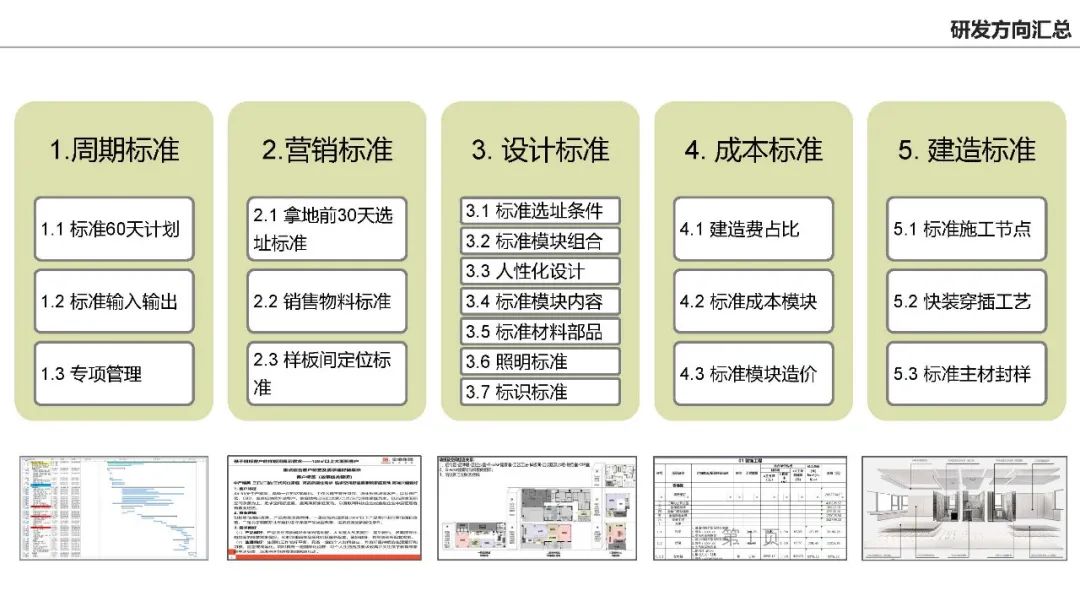
专家分享 | 租赁型售楼处标准化示范区提效研究
2023年2月8日上午,优积科技邀请原金地集团北京公司 高级室内设计专业应锎经理为我司团队分享《租赁型售楼处标准化示范区提效》的专题。 此次专家分享课题加上大家踊跃讨论时间长达3小时,会上应总详细介绍了租赁型售楼处标准化示范区提效,需…...
linux之echo使用技巧
参考文章:linux基本功系列-echo命令实战一、echo 命令是什么?作用: echo命令能将指定文本显示在Linux命令行上,或者通过重定向符写入到指定的文件中。语 法:echo [-ne][字符串] / echo [–help][–version]补充说明&am…...

Keras实例教程(7)之构建模型的第三种方式
多年以前,在TensorFlow中搭建深度学习模型对于很多人来说其实仍然是比较困难的。相比之下,Keras作为独立于TensorFlow的一种深度学习框架则要简单很多。在TensorFlow与PyTorch的竞争中逐渐式微的情况下,TensorFlow团队终于宣布Keras将成为在tensorflow2.0中构建和训练模型的…...
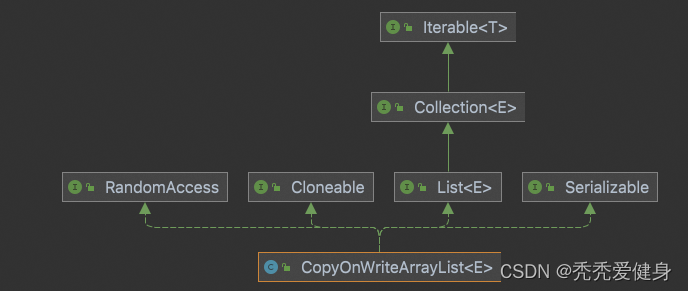
【JUC并发编程】18 CopyOnWriteArrayList源码也就够看2分钟
文章目录1、CopyOnWriteArrayList概述2、原理 / 源码1)构造函数2、add()3)get()4)remove()5)iterator()1、CopyOnWriteArrayList概述 CopyOnWriteArrayList相当于线程安全的ArrayList,底层是一个可变数组。 特点如下…...

如何优雅的实现回调函数?
本篇文章又是一期优雅的代码编程介绍———回调函数。 传统的nodejs编程都是这样的 const fs require(fs) fs.readFile(test.txt,utf8, function(err, dataStr){if(err){} }) 嵌套层级如果多了就成回调地狱了。如果我们将这种风格的代码转换成这样呢? const fs …...
))
3GPP-NR Band20标准定义频点和信道(3GPP V17.7.0 (2022-12))
Reference test frequencies for NR operating band n20 Table 4.3.1.1.1.20-1: Test frequencies for NRoperating band n20 and SCS 15 kHz CBW [MHz]carrierBandwidth...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
