Diffusion model(三): 公式结论
接上文
Diffusion model(一): 公式推导详解
这一节主要总结之前文章的公式结论
1. 已知x0x_{0}x0时,sample过程的均值和方差
q(xt−1∣xt,x0)=(xt−1;μ~(xt,x0),β~tI)\begin{aligned} q(x_{t-1}|x_{t}, x_{0}) = \mathcal(x_{t-1}; \tilde{\mu}(x_{t}, x_{0}), \tilde{\beta}_{t}I) \end{aligned} q(xt−1∣xt,x0)=(xt−1;μ~(xt,x0),β~tI)
得到
{β~t=1−α‾t−11−α‾t⋅βtμ~t(xt,x0)=αt(1−α‾t−1)1−α‾txt+α‾t−1βt1−α‾tx0\left\{ \begin{array}{ll} \tilde{\beta}_{t} = \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_{t}} \cdot \beta_{t} \\ ~~ \\ \tilde{\mu}_{t}(x_{t}, x_{0}) = \frac{\sqrt{\alpha_{t}}(1-\overline{\alpha}_{t-1})}{1-\overline{\alpha}_{t}}x_{t} + \frac{\sqrt{\overline{\alpha}_{t-1}}\beta_{t}}{1-\overline{\alpha}_{t}}x_{0} \end{array} \right. ⎩⎨⎧β~t=1−αt1−αt−1⋅βt μ~t(xt,x0)=1−αtαt(1−αt−1)xt+1−αtαt−1βtx0
2. 已知xtx_{t}xt以及预测噪声ϵ\epsilonϵ,计算x0x_{0}x0
注意这里的噪声是xt−1x_{t-1}xt−1到xtx_{t}xt增加的噪声,已知xt=α‾tx0+1−α‾tz‾tx_{t} = \sqrt{\overline{\alpha}_{t}}x_{0} + \sqrt{1-\overline{\alpha}_{t}}\overline{z}_{t}xt=αtx0+1−αtzt,得
x0=1α‾txt−1−α‾tα‾tztx_{0} = \frac{1}{ \sqrt{\overline{\alpha}_{t}}} x_{t} - \frac{\sqrt{1-\overline{\alpha}_{t}}}{\sqrt{\overline{\alpha}_{t}}} {z}_{t} x0=αt1xt−αt1−αtzt
相关文章:
: 公式结论)
Diffusion model(三): 公式结论
接上文 Diffusion model(一): 公式推导详解 这一节主要总结之前文章的公式结论 1. 已知x0x_{0}x0时,sample过程的均值和方差 q(xt−1∣xt,x0)(xt−1;μ~(xt,x0),β~tI)\begin{aligned} q(x_{t-1}|x_{t}, x_{0}) \mathcal(x_{t-1}; \tilde{\mu}(x_{t}, x_{0}),…...
组件)
Angular笔记(二)组件
组件包括: HTML 模板: 声明页面渲染的内容TypeScript 类: 定义行为CSS 选择器: 定义组件在模板中的使用方式(可选)要应用在模板上的 CSS 样式 一、 创建组件: 使用 Angular CLI 创建一个组件 ng generate component <component-name>…...

微信小程序|基于小程序+C#制作一个超酷的个人简历
你还在用以前的方式投简历吗?趁着金三银四来临之际,跟随此文使用小程序制作一个便携超酷的个人简历,高调炫技,愉快的收offer吧! 一、小程序...
)
华为OD机试 - 最快到达医院的方法(Java JS Python)
题目描述 新型冠状病毒疫情的肆虐,使得家在武汉的大壮不得不思考自己家和附近定点医院的具体情况。 经过一番调查,大壮明白了距离自己家最近的定点医院有两家。其中: 医院A和自己的距离是X公里医院B和自己的距离是Y公里由于武汉封城,公交停运,私家车不能上路,交通十分不…...
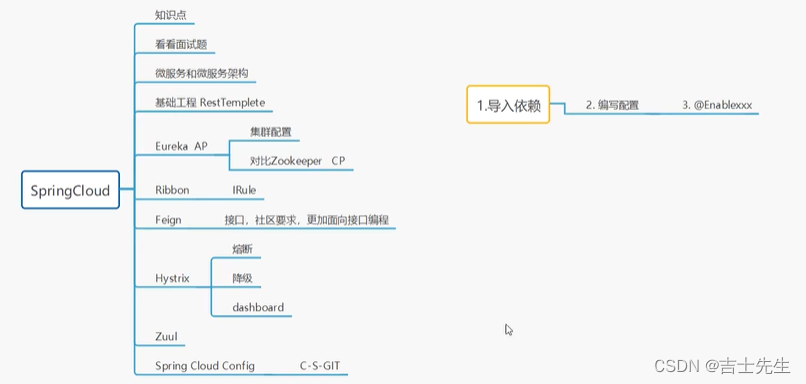
92.【SpringCloud NetFilx】
SpringCloud(一)、这个阶段该如何学习?1.微服务介绍2.面试常见问题(二)、微服务概述1.什么是微服务?2. 微服务与微服务架构(1).微服务(2).微服务架构⭐(3). 微服务优缺点(4). 微服务技术栈有那些?(5). 为什么选择SpringCloud作为微服务架构(三)、SpringCloud入门概…...

[ahk]如何载入Scite的会话Session文件
加载session文件的AutoHotkey代码:oSciTE : ComObjActive("SciTE4AHK.Application") messageloadsession:d:\\ddd\\2023-2-15SciTE.session oSciTE.SendDirectorMsg(message)存储session文件的AutoHotkey代码:messagesavesession:d:\\ddd\\123…...

MyISAM和InnoDb的区别
MySQL 5.0以后的版本默认的存储引擎为InnoDb,之前是MyISAM。 现在说说两者的区别: 1.数据存储结构的不同 MyISAM存储文件:.MYD(存储表数据),.MYI(存储表结构),.FRM(存储表结构) InnoDb存储文件: .FRM(存储表结构)&am…...
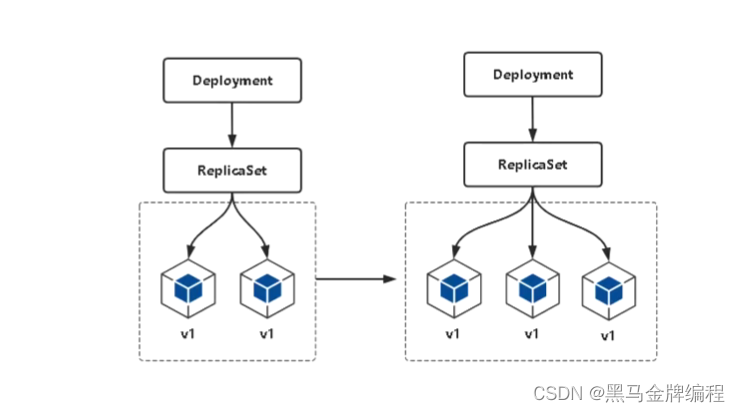
K8s管理应用生命周期-Deployment篇
在k8s中部署应用程序流程 1、使用Deployment部署Java应用 kubectl create deployment web --imageXXX/java-demokubectl get deployment,pods 2、使用Service发布Pod kubectl expose deployment web --port80 --typeNodePort --target-port8080 --namewebkubectl get servic…...
类和对象(下)(二)
类和对象(下)(二)1.友元1.1友元函数1.2友元类2.内部类3.拷贝对象时的一些编译器优化(vs2022)🌟🌟hello,各位读者大大们你们好呀🌟🌟 🚀…...
)
MapBox-draw绘制插件的使用教程(含修改样式和方法封装)
mapbox-draw插件是官方推荐的用于支持在mapbox地图中绘制图形的插件库。好像并不是由官方编写的,但是官方觉得其好用就直接推荐大家也使用了,我用了2天感觉下来还是觉得很鸡肋。对于开发者来讲自由修改的程度不是很高。这篇文章简单说一下对于mapbox-draw的使用和修改。 第一…...
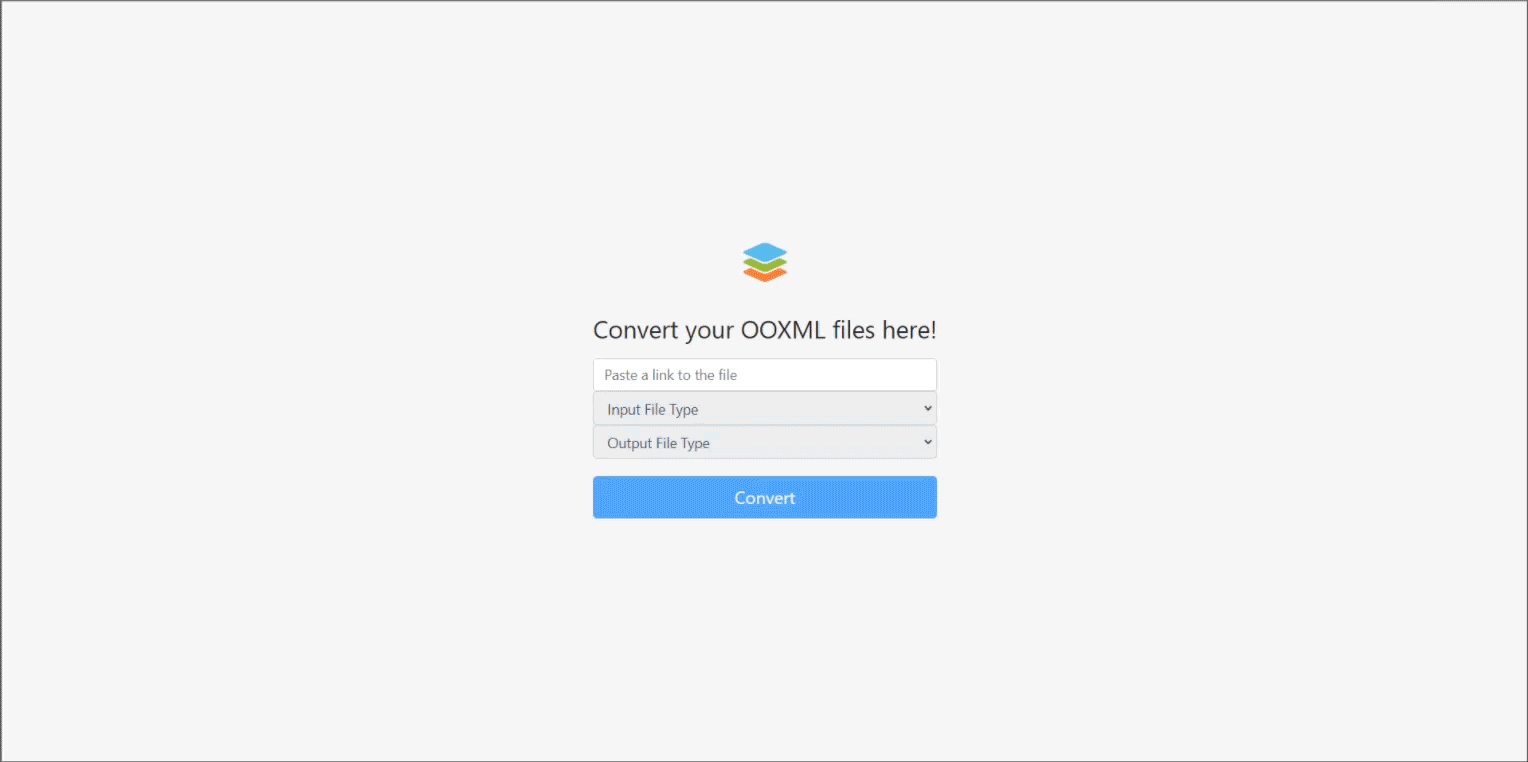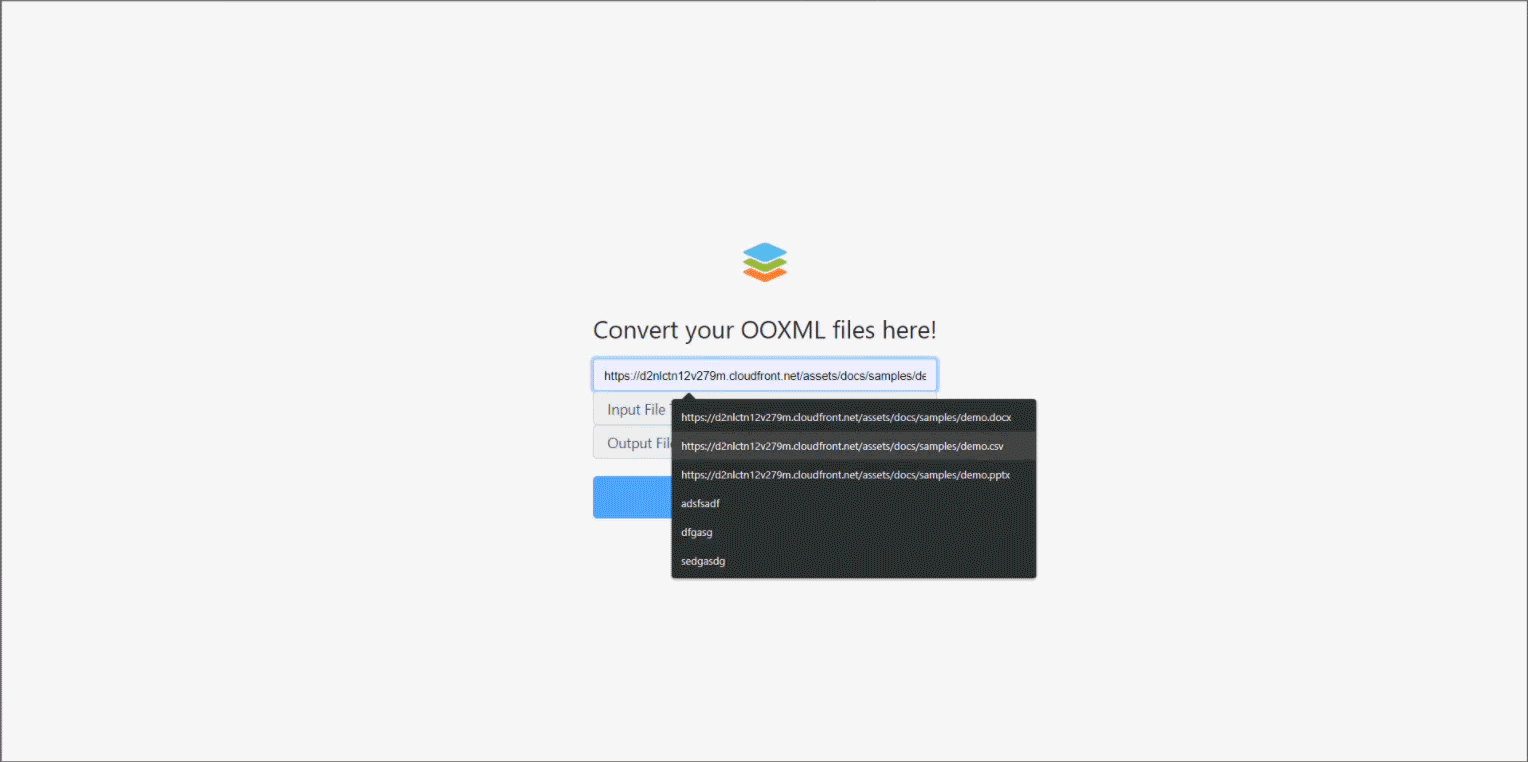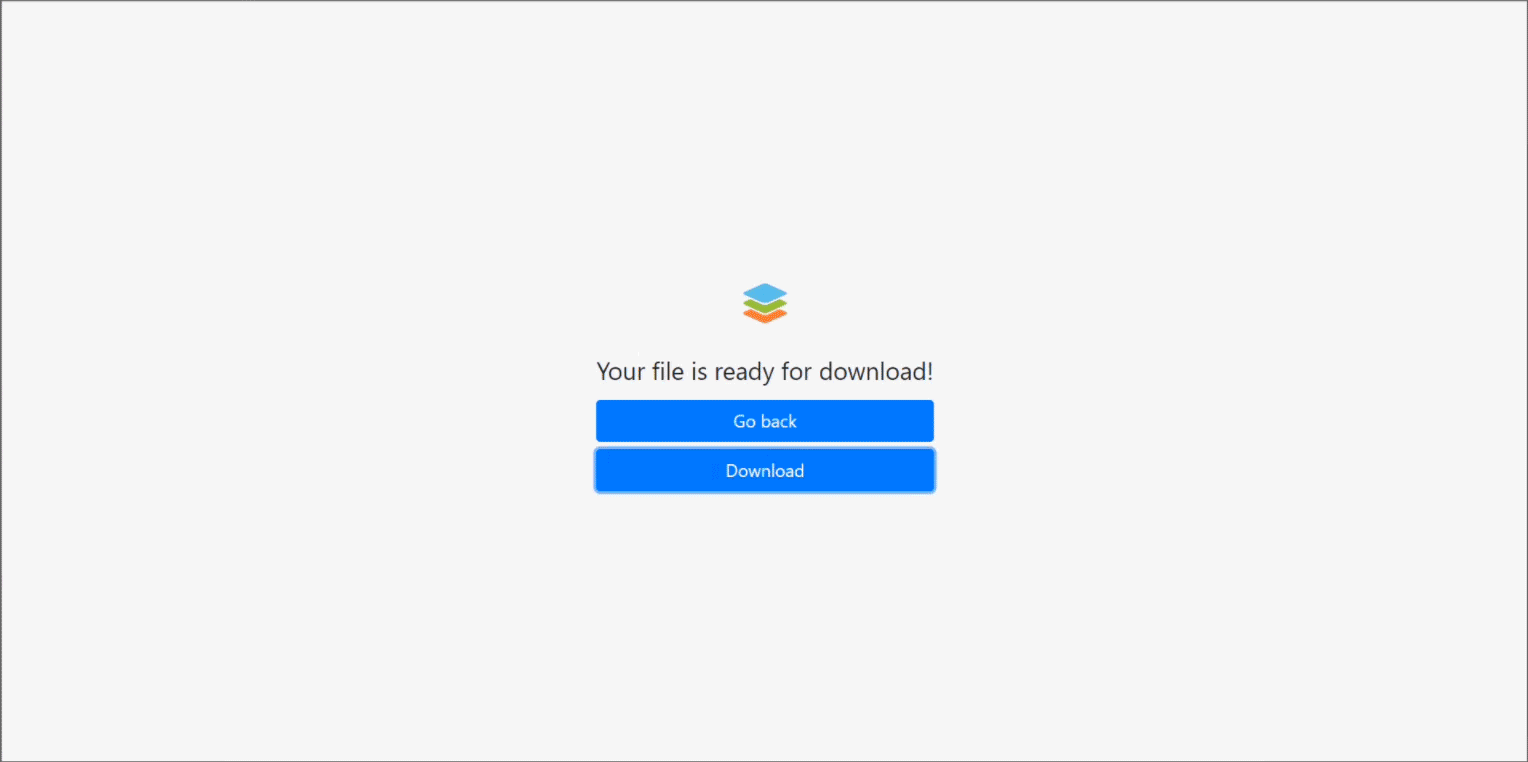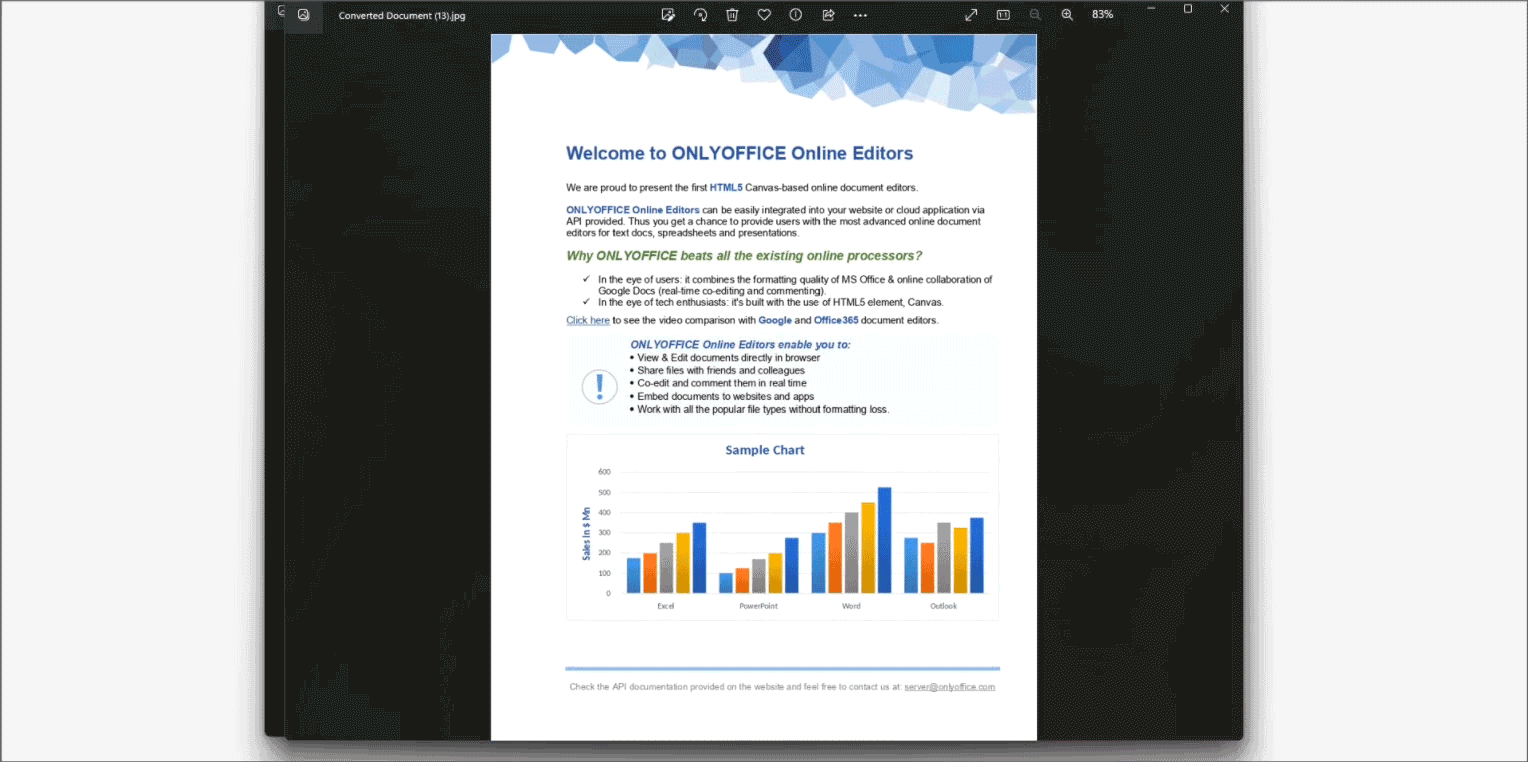
使用 ONLYOFFICE 转换 API 构建在线文档转换器
文档转换是非常常用、非常有价值的功能,可以帮助我们处理多种文档类型。ONLYOFFICE 编辑器可以轻松地将文档转换为多种格式。在这篇博文中,我们会向您展示,如何构建在 ONLYOFFICE 转换 API 上运行的在线转换器。 关于 ONLYOFFICE 转换 API 使…...

Kubernetes的负载均衡方案:MetalLB
私有云裸金属架构(这是相对云上环境来说,不是说无操作系统)上部署的 Kubernetes 集群,通常是无法使用 LoadBalancer 类型的 Service 的。因为 Kubernetes 本身没有为裸机群集提供网络负载均衡器的实现。 如果你的 Kubernetes 集群没有在公有云的 IaaS 平台(GCP,AWS,Azu…...
【项目】Vue3+TS CMS 基本搭建相关配置
💭💭 ✨:Vue3 TS 💟:东非不开森的主页 💜: today beginning💜💜 🌸: 如有错误或不足之处,希望可以指正,非常感谢😉 基本…...

ros2 dds
问题1: fastdds发布的类型,ros2接收不到 原因: 在QoS相互兼容情况下,无法通信是由于idl类型没有使用兼容ros2的格式。如用 ros2 topic list -t 查看时,会发现同一个topic有两个不同的类型,如DDS会显示:myclass::peo…...

chain33架构介绍
chain33架构介绍 Chain33构架主要分为五个层级:数据层、网络层、共识层、激励层及应用层。 应用层:兼容以太坊智能合约,支持发行代币、资产交易、钱包找回,hash锁定等原生能力,同时支持用户可扩展执行器(…...

Lucene学习笔记
lucene结构 索引:概念上的一个表,现实体现就是一个文件目录,一个目录代表一个索引,也视作documents文档集合 文档:document,为索引中的一条数据,一个document可以拥有多个filed(域&a…...

动态规划【Day01】| 669 · 换硬币、114 · 不同的路径、116 · 跳跃游戏
秘诀:确定状态转移方程初始条件和边界情况计算顺序 669 换硬币 669 换硬币 题目描述: 给出不同面额的硬币以及一个总金额. 写一个方法来计算给出的总金额可以换取的最少的硬币数量. 如果已有硬币的任意组合均无法与总金额面额相等, 那么返回 -1。 样…...

1.Hello Python
Python Python 在网络爬虫、数据分析、AI、机器学习、Web开发、金融、运维、测试等多个领域都有不俗的表现,从来没有哪一种语言可以同时在这么多领域扎根。 Python基本语法 python关键字 关键字即保留字,和其他语言一样,这些关键字…...
C语言实例|编写C程序在控制台打印余弦曲线
C语言文章更新目录 C语言学习资源汇总,史上最全面总结,没有之一 C/C学习资源(百度云盘链接) 计算机二级资料(过级专用) C语言学习路线(从入门到实战) 编写C语言程序的7个步骤和编程…...

《Hadoop篇》------大数据及Hadoop入门
目录 一、大数据及Hadoop入门 1.1 单节点、分布式、集群 1.1.1 大数据的概念 1.1.2 大数据的本质 二、HDFS Shell命令 2.1、常用相关命令 2.2、上传文件 2.2.1、上传文件介绍 2.2.2上传文件操作 2.3、下载文件 2.4、删除文件 2.5、创建目录 2.6、查看文件系统 2.…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
