DataWhale-统计学习方法打卡Task01
学习教材《统计学习方法(第二版)》李航
统计学习方法(第2版) by...李航 (z-lib.org).pdf https://www.aliyundrive.com/s/maJZ6M9hrTe 点击链接保存,或者复制本段内容,打开「阿里云盘」APP ,无需下载极速在线查看,视频原画倍速播放。
学习内容:第1章 统计学习及监督学习概论
学习视频:B站视频
第一章 统计学习及监督学习概论 1.1-统计学习_哔哩哔哩_bilibili
【合集】十分钟 机器学习 系列视频 《统计学习方法》_哔哩哔哩_bilibili
第1章 统计学习及监督学习概论
定义:监督学习是从标注数据中心学习模型的机器学习问题,是统计学习或机器学习的额重要组成部分。
1.1 统计学习
1. 统计学习的特点
统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科。
2.统计学习的对象
统计学习的对象是数据data。包括数字、文字、图像、视频、音频数据以及他们的组合。
统计学习的假设,是同类数据具有一定的统计规律性。这是统计学习的前提。
3.统计学习的目的
统计学习用于对数据的预测和分析,特别是对位置新数据的预测与分析。
4. 统计学习的方法
监督学习(supervised learning), 无监督学习(unsupervised learning), 强化学习(reinforecement learning).
学习统计学习方法的步骤:
(1)得到一个有限的训练数据集和;
(2)确定包含所有可能模型的假设空间,即模型的集合;
(3)确定模型选择的准则,即学习的策略;
(4)实现求解最优模型的算法,即学习的算法;
(5)通过学习的方法选择最优模型;
(6)利用学习的最优模型对新数据进行预测或分析。
5.统计学习的研究
6.统计学习的重要性
1.2 统计学习的分类
1.2.1基本分类
1. 监督学习
监督学习是指从标注数据中学习预测模型的机器学习问题。
(1)输入空间、特征空间和输出空间
输入输出变量用大写字母表示,习惯上输入变量写作,输出变量写作
。输入输出变量的取值用小写字母表示,输入变量的取值写作
,输出变量的取值写作
。变量可以是标量或向量,都用相同类型字母表示。除特别说明外,本书中向量均为列向量,输入实例
的特征向量记做:
表示
的第
个特征。注意
与
不同,本书中通常用
表示多个输入变量中第
个变量,即
监督学习从训练数据training data集合中学习模型,对测试数据test data进行预测,训练数据有输入输出对组成。
输入变量和输出变量
有不同的类型,可以是连续的也可以是离散的。输入变量与输出变量均为连续变量的预测问题为回归问题;输入变量为有限个离散变量的预测问题称为分类问题;输入变量与输出变量均为变量序列的预测问题称为标注问题。
(2)联合概率分布
监督学习假设输入与输出的随机变量和
遵循联合概率分布
。
表示分布函数或分布密度函数。假设训练数据与测试数据被看做是依联合概率分布
独立同部分产生的。
(3)假设空间
模型输入由输入空间到输出空间的映射集合,这个集合就是假设空间(hypothesis space)。假设空间的确定意味着学习范围的确定。
监督学习的模型可以是概率模型或非概率模型,由条件概率分布或决策函数(decision function)
表示,随具体学习方法而定。
(4)问题的形式化
监督学习分为学习和预测两个过程,由学习系统和预测系统完成,可用图1.1来描述
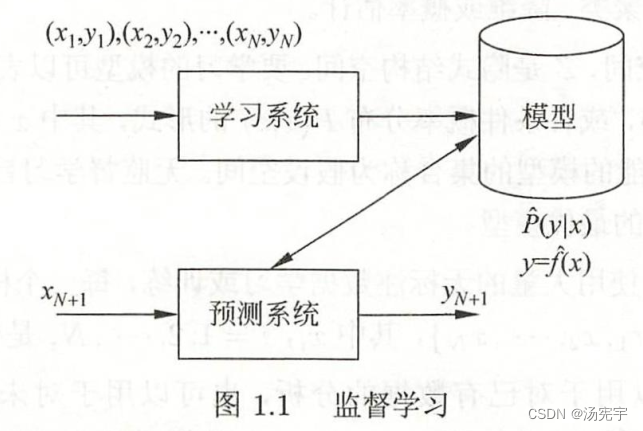
首先给定一个训练集
其中,称为样本或样本点。
是输入的观测值,也称为输入或实例,
是输出的观测值,也称为输出。
监督学习分为学习和预测两个过程,有学习系统和预测系统完成。在学习过程中,学习系统利用给定的数据集,通过学习得到一个模型,表示为条件概率分布或决策函数
。在预测过程中,预测系统对于给定的测试样本集中的输入
由模型
或
给出相应的
。
2.无监督学习
无监督学习(unsupervised learning)是指从无标注数据汇总学习预测模型的机器学习问题。无监督学习的本质是学习数据中心的统计规律或潜在结构。预测模型表示数据的类别、转换或概率。
模型可以是实现对数据的聚类、降维或概率估计。
无监督学习通常使用大量的无标注数据学习或训练,每一个样本是一个实例。训练数据表示为
其中
是样本。
无监督学习可以对已有数据分析,也可以用于对未来数据的预测。分析师使用学习得到的模型即函数, 条件概率分布
或条件概率分布
。

备注:表示在使概率P最大时,z的取值。
3.强化学习
强化学习(reinforcement learning)是指智能系统在于环境的连续互动中学习最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔科夫决策过程(Markov decision process),智能系统能观测到的是与环境互动得到数据序列。强化学习的本质是学习最优的序贯决策。
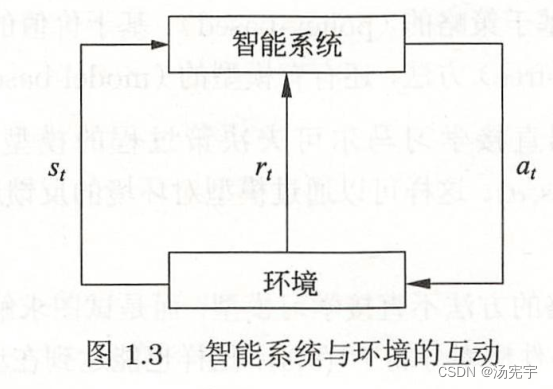
强化学习没有研究过,此书中好像也没有相关的章节,此处略过,后续学习的时候再补上。
4.半监督学习与主动学习
半监督学习是指利用标注数据和未标注数据学习预测模型的机器学习问题。
主动学习是指机器不断主动给出实例让教师进行标注,然后李永彪主数据学习预测模型的机器学习问题。
1.2.2按模型分类
统计学习或机器学习方法可以根据其模型的种类进行分类。
1. 概率模型与非概率模型。
统计学习的模型可以分为概率模型(probabilistic model)和非概率模型(non-probabilistic model)或确定性模型(deterministic model)。
在本书介绍的决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型是概率模型。感知机、支持向量机、k近邻、Adaboost、k均值、潜在语义分析,以及神经网络是非概率模型。逻辑斯蒂回归即可以看做概率模型,又可以看做非概率模型。
2.线性模型与非线性模型
这个比较容易理解。
3.参数化模型与非参数模型
参数化模型假设模型参数的维度固定,模型可以由有限维完全刻画;非参数模型假设模型参数的纬度不固定或者说无穷大,随着训练数据量的增加二不断增大。
1.2.3按算法分类
统计学习根据算法,可以分为在线学习与批量学习。在线学习值每次接受一个样本,进行预测,之后学习模型,并不断重复该操作的机器学习。与之对应,批量学习一次接受所有数据,学习模型,之后进行预测。

1.2.4按技巧学习
1. 贝叶斯学习
朴素贝叶斯、潜在狄利克雷分配的学习属于贝叶斯学习。
假设随机变量D表示数据,随意变量表示模型参数。根据贝叶斯定理,可以用以下公式计算后验概率
:
其中是先验概率,
是似然函数。
此处看不太懂,等到后面学习贝叶斯的时候再进行深入研究
2.核方法
核方法(kernel method)时使用核函数表示和学习非线性模型的一种机器学习方法,可以用于监督学习和无监督学习。
1.3 统计学习方法三要素
统计学习方法都是由模型、策略和算法构成的,即统计学习方法由三要素构成,可以简单表示为:
方法=模型+策略+算法
1.3.1模型
在监督学习过程胡总,模型就是us噢要学习的条件概率分布或决策函数。模型的假设空间(hypothesis space)包含所有可能的条件概率分布或决策函数。
假设空间用表示。假设空间可以定义为决策函数的集合:
其中,X和Y是定义在输入空间和输出空间
上的变量。这是
通常是一个参数向量决定的函数族:
参数向量取值与n维欧式空间
,称为参数空间(parameter space)
1.3.2策略
1.损失函数和风险函数
监督学习问题是在假设空间中选取模型
作为决策函数,对于给定的输入X,由
给出相应的输入Y,这个输出的预测值与真实值Y可能一致也可能不一致,用一个损失函数loss function 或代价函数cost function来度量预测错误的程度。损失函数是
和Y的非负实值函数,记做
(1)0-1损失函数
(2)平方损失函数(quadratic loss function)
(3)绝对值损失函数(absolute loss function)
(4)对数损失函数(logarithmic loss function)或对数似然损失函数
损失函数值越好,模型就越好。由于模型的输入、输出(X,Y)是随机变量,遵循联合分布P(X,Y), 所以损失函数的期望是
这是理论上模型关于联合分布
的平均意义下的损失,称为风险函数(risk function)或期望损失(expected loss)。
学习的目标就是选择期望风险最小的模型。
给定一个训练数据集,模型
关于训练数据集的平均损失函数称为经验风险(empirical risk)或经验损失(empirical loss),记做
根据大数定律,当样本容量N趋近于无穷大时,经验风险趋于期望风险
。这就关系到监督学习的连个策略:经验风险最小化和结构风险最小化。
2.经验风险最小化与结构风险最小化
经验风险最小化(empirical risk minimization, ERM)策略认为,经验风险最小的模型是最优的模型。
但是挡烟本很小时,经验风险最小化学习的效果未必很好,会产生“过拟合”现象。
结构风险最小化(Structural risk minimization, SRM)是为了防止过拟合而提出的策略。结构风险最小化等价于正则化(Regularization)。结构风险在经验风险上加上表示模型复杂度的正则化项和惩罚项。
其中为模型的复杂度,是定义在假设空间
上的泛函。模型
越复杂,复杂度
就越大;反之,模型
越简单,复杂度
就越小。也就是说,复杂度表示了对复杂模型的惩罚。
是系数,用以权衡经验风险和模型复杂度。结构风险小需要经验风险和模型复杂度同时小。结构风险小的模型往往对训练数据以及位置的测试数据都有较好的预测。
1.3.3算法
算法是指学习模型的具体方法。
1.4模型评估与模型选择
1.4.1训练误差与测试误差
假设学习到的模型是,训练误差是模型
关于蓄念书籍的平均损失:
测试误差是模型关于测试数据集的平均损失:
1.4.2过拟合与模型选择
过拟合是指学习时选择的模型所包含的参数过多,以至于出现这一模型对于已知数据预测很好,对位置数据预测很差的现象。可以说模型选择旨在避免过拟合并提高模型的预测能力。
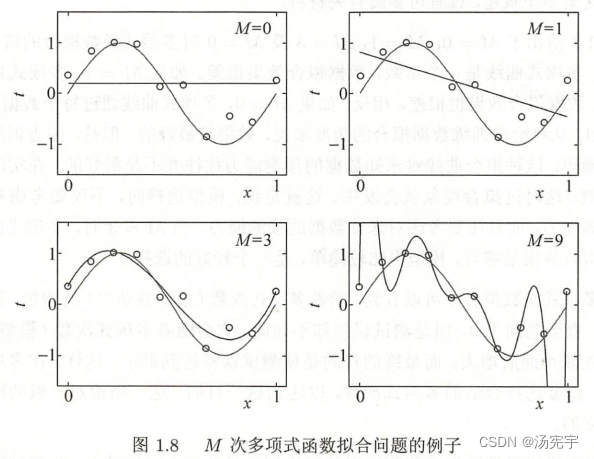
1.5正则化与交叉验证
1.5.1正则化
模型选择的典型方法是正则化。正则化是结构风险最小化策略的实现,是在经验风险上加上一个正则化项或惩罚项。
其中第一项是经验风险,第二项是正则化项,为调整两者之间关系的系数。
正则化可以取不同的形式。有范数。
这里表示参数向量w的
范数。
正则化项也可以是参数向量的范数:
正则化符合奥卡姆剃刀原理。奥卡姆剃刀原理应用于模型选择时变为一下想法:在所有可能选择的模型中,能够很好解释已知数据并且十分简单才是最好的模型,也就是应该选择的模型。
1.5.2交叉验证
另外一种常用的模型选择方法是交叉验证(cross validation)。
将数据集切分为三部分,训练集(training set),验证集(validation set)和测试集(test set)。训练集训练模型,验证集用于模型的选择,二测试集用于对最终学习方法的评估。
1.简单交叉验证
2.S折交叉验证
3.留一交叉验证
1.6泛化能力
1.6.1泛化误差
学习方法的泛化能力是指该方法学习到的模型对位置数据的预测能力,是学习方法本质上重要的性质。现实中采用最多的办法是通过测试误差来评价学习方法的泛化能力。
下面是泛化误差的证明,此处省略没看。
1.6.2泛化误差上界
1.7生成模型与判别模型
监督学习方法又可以分为生成方法(generative approach)和判别方法(discriminative approach)。所学到的模型分别称为生成模型和判别模型。
生成方法有数据学习联合概率分布,然后求出条件概率分布
作为预测的模型,即生成模型:
这样的方法之所以称为生成方法,是因为模型表示了给定输入X产生输出Y的生成关系。典型的生成模型有朴素贝叶斯法和隐马尔可夫模型。
判别方法由数据直接学习决策函数或者条件概率分布
作为预测的模型,即判别模型。
1.8监督学习的应用
监督学习分为:分类问题,标注问题和回归问题。
1.8.1分类问题
在监督学习中,当输出Y取有限个离散值时,预测问题便成为分类问题。分类问题的过程如下:

对于二分类问题评价指标是精确率precision和召回率recall。
TP-----将正类预测为正类
FN-----将正类预测为负类
FP-----将负类预测为正类
TN-----将负类预测为负类
精确率定义为:
召回率定义为:
此外还有F1值,是精确率和召回率的调和均值,即
1.8.2标注问题
标注(tagging)也是一个监督问题。可以认为标注问题是分类问题的一个推广,标注问题优势更复杂的结构预测问题的简单形式。标注问题的输入是一个观测序列,输出是一个标记序列或状态序列。标注问题的目标在于学习一个模型,使它能够对观测序列给出标记序列作为预测。

1.8.3回归问题
回归是监督学习的另一个重要问题。回归用于预测输入变量和输出变量之间关系,特别是当输入变量的发生变化时,输出变量的值随之发生变化。
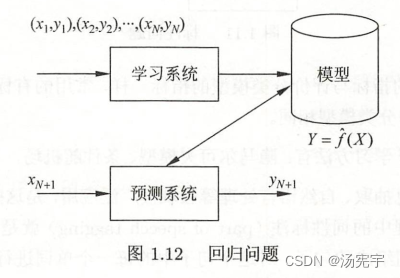
回归问题可以分为一元回归和多元回归;按照输入变量和输出变量之间的关系可以分为线性回归和非线性回归。
课后习题
习题1.1
说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素。伯努利模型是定义在取值为0与1的随机变量上的概率分布。假设观测到伯努利模型�n次独立的数据生成结果,其中�k次的结果为1,这时可以用极大似然估计或贝叶斯估计来估计结果为1的概率。
解:
第一步:伯努利模型
伯努利方程模型定义为:
其中p为随机变量X取值为1的概率,1-p为取0的概率。
则X的概率分布为:
则伯努利的假设空间为:
第二步:伯努利模型的极大似然估计及毕业四估计中的统计学习方法三要素
(1)极大似然估计
模型:伯努利模型
策略:经验风险最小化。极大似然估计,等价于当模型是条件概率分布、损失函数是对数损失函数时的经验风险最小化。
算法:极大化似然,
(2)贝叶斯估计
模型:伯努利模型
策略:结构风险最小化。贝爷估计中的最大后验概率估计,等价于当模型条件是概率分布、损失函数是对数损失函数、模型复杂度有模型的先验概率表示时的风险结构最小化。
算法:最大化后验概率:
第三步:伯努利模型的极大似然估计
对于伯努利模型,可得似然函数:(在n次独立的数据中,k次结构为1,n-k次结构为0)
对似然函数取对数,得到对数似然函数:
求解参数p:
对参数p求导,可求解倒数为0时的p的值:
令
从上式可得即
所以
步骤四:伯努利模型的贝叶斯估计(没看懂)
习题1.2
通过经验风险最小化推导极大似然估计。证明模型是条件概率分布,当损失函数是对数损失函数时,经验风险最小化等价于极大似然估计。
解:
假设模型的条件概率分布是,样本集
,对数损失函数为:
按照经验风险最小化求最优模型就是最优解的结论可得出:
综合上面两个式子可得经验风险最小化函数:
根据似然函数定义:,以及极大似然函数的一般步骤,可得:
相关文章:
DataWhale-统计学习方法打卡Task01
学习教材《统计学习方法(第二版)》李航 统计学习方法(第2版) by...李航 (z-lib.org).pdf https://www.aliyundrive.com/s/maJZ6M9hrTe 点击链接保存,或者复制本段内容,打开「阿里云盘」APP ,无…...
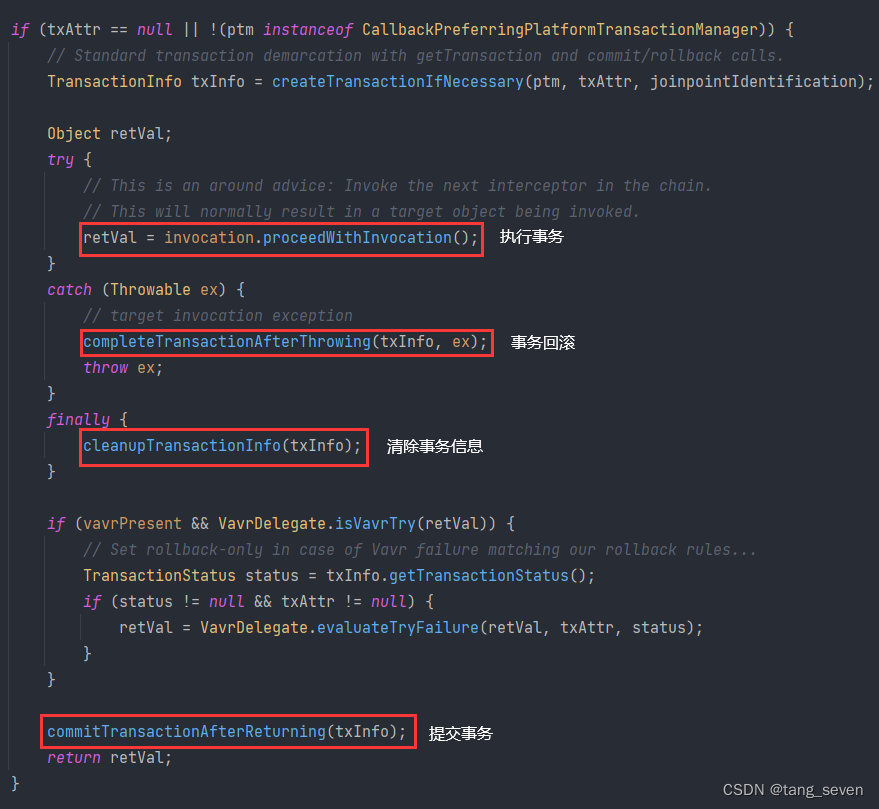
Java面试——Spring 事务
目录 1.什么是Spring 事务 2.Spring 事务的开启方式 3.Spring事务的实现方式/原理 4.事务传播机制 5.事务隔离级别 6.事务失效的原因 1.什么是Spring 事务 事务在逻辑上是一组操作,要么执行,要不都不执行。 如下: Begin; insert into…...
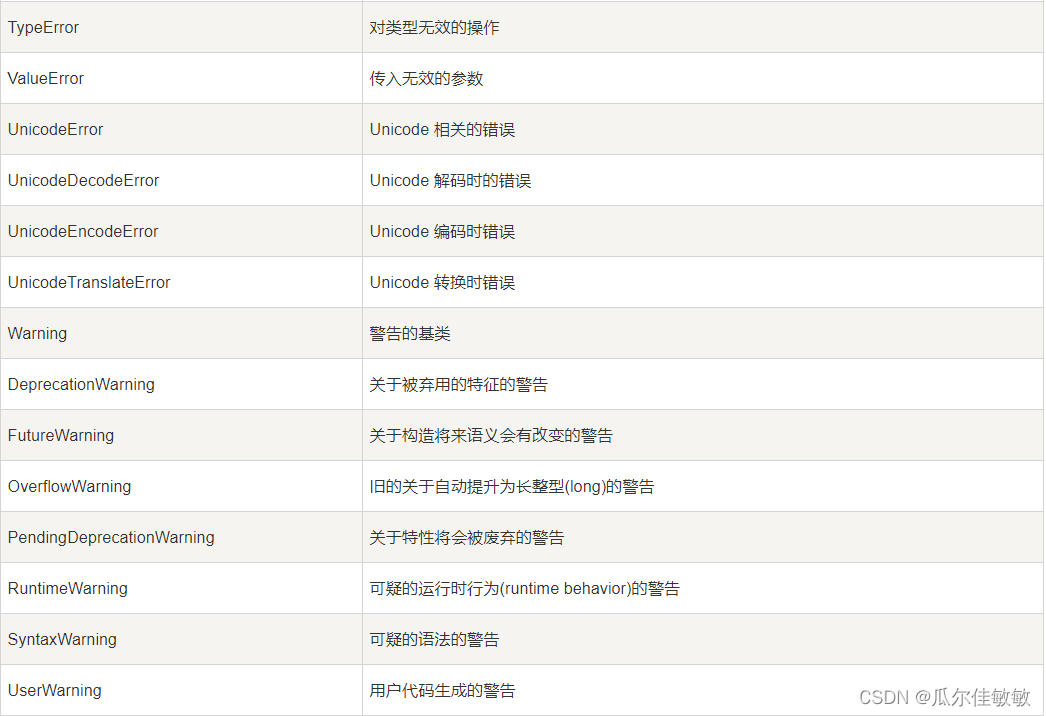
Python语言零基础入门教程(十九)
Python 异常处理 python提供了两个非常重要的功能来处理python程序在运行中出现的异常和错误。你可以使用该功能来调试python程序。 1、异常处理 2、断言(Assertions) python标准异常 什么是异常? 异常即是一个事件,该事件会在程序执行过程中发生&…...
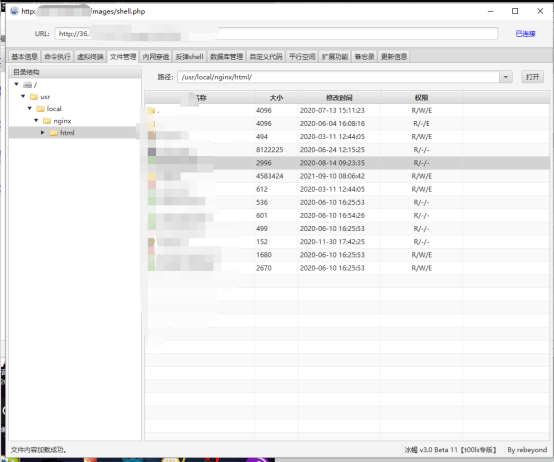
重生之我是赏金猎人-SRC漏洞挖掘(一)-某SRC测试系统无脑Getshell
0x01 前言 https://github.com/J0o1ey/BountyHunterInChina 欢迎大佬们点个star 0x02 资产收集到脆弱系统 在某src挖掘过程中,本人通过ssl证书对域名资产进行了收集,通过计算域名对应ip段的权重 整理出其C段资产,进行了批量目录扫描 查看…...

Sciter 结合 PReact 实现组件公共逻辑抽离
Sciter 结合 PReact 实现组件公共逻辑抽离 下面例子是获取鼠标移动位置,将这部分逻辑进行抽离 一、使用高阶组件抽离公共逻辑 import {Component } from ./preact.js; export const HOCFactory = (Component) => {class HOC...
OpenTracing协议规范链接
一、官网链接 OpenTracing specificationhttps://opentracing.io/specification/不过目前OpenTracing项目已归档,不再维护。需要参考OpenTelemetry官网链接 Migrating from OpenTracing | OpenTelemetryBackward compatibility with OpenTracing has been a prior…...
金三银四面试必看,自动化测试如何解决日志问题
前言 前几天在员群里,有同学问了一个自动化测试实践中遇到的问题: 持续集成的自动化用例很多,测试环境日志level为debug,日志量大概40G/每天,定位问题时日志查询很慢,该怎么解决? 这个问题可…...
微信怎么开小店?【企业商家微信开店】
企业商家入局微信做营销已经是经营规划中必须做的一件事了,对于企业商家来说,最简单直接的方式就是开一个微信小店,然后通过自己宣传推广来在微信小店中成商品。那么企业商家在微信怎么开小店呢?下面内容分享给想在微信开店的企业…...

Java 中FastJson的使用【吃透FastJson】
如果不了解JSON格式,建议先看下:JSON数据格式【学习记录】 JSON序列化、反序列化JavaBean的框架有很多,最常见的Jackson、阿里巴巴开源的FastJson、谷歌的GSON、apache提供的json-lib等,下面我们主要来熟悉一下:Java语…...

Redis5.0集群搭建
Redis集群教程 此文重在介绍 Redis5.0 三主三从集群安装,无复杂难懂的概念,若想深入了解集群原理请参考Redis集群规范。 Redis集群介绍 Redis Cluster 提供一种 Redis 安装方式:数据自动在多个 Redis 节点间分片。 Redis Cluster 提供一定…...
继企业级信息系统开发学习1.1 —— Spring配置文件管理Bean
骑士救美计划采用构造方法注入属性值1、创建救美任务类2、创建救美骑士类2、创建救美骑士类3、创建旧救美骑士测试类3、配置救美骑士Bean5、创建新救美骑士测试类采用构造方法注入属性值 1、创建救美任务类 在net.huawei.spring.day01包里创建RescueDamselQuest类 Rescue Da…...
Web 容器、HTTP 服务器 、Servlet 容器区别与联系
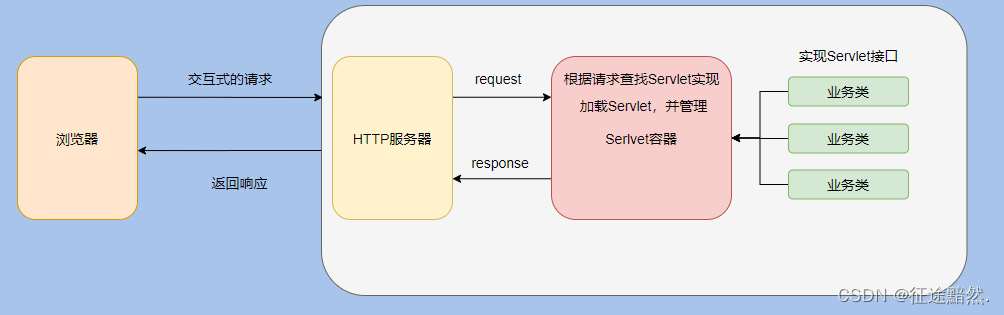
首先浏览器发起 HTTP 请求,像早期的时候只会请求一些静态资源,这时候需要一个服务器来处理 HTTP 请求,并且将相应的静态资源返回。 这个服务器叫 HTTP 服务器。 简单点说就是解析请求,然后得知需要服务器上面哪个文件夹下哪个名字…...

eBPF 进阶: 内核新特性进展一览
Linux 内核在 2022 年主要发布了 5.16-5.19 以及 6.0 和 6.1 这几个版本,每个版本都为 eBPF 引入了大量的新特性。本文将对这些新特性进行一点简要的介绍,更详细的资料请参考对应的链接信息。总体而言,eBPF 在内核中依然是最活跃的模块之一&a…...

2.输入子系统学习-multi-touch-protocol-2023.02
Documentation/input/multi-touch-protocol.txt(百度翻译) Multi-touch (MT) Protocol ------------------------- Copyright (C) 2009-2010 Henrik Rydberg <rydbergeuromail.se> 一、Introduction ------------ In order to utilize t…...
【靶机】vulnhub靶机pylington
靶机下载地址 Pylington: 1 ~ VulnHub kali ip:192.168.174.128 靶机ip:192.168.174.146 arp-scan -l发现靶机ip是192.168.174.146 进行靶机的端口扫描,这里使用的是nmap的gui 可以发现开放了21和80端口,80端口扫描到了robot…...

【大数据】大数据学习路线
职位选择 首先明确一点:大数据涉及的知识面广度还是有的,需要学习的组件繁多,想要每一项精通几乎不可能,所以企业在招聘的时候会进行细分,基于某个方向进行招聘,比如关键字,数据仓库工程师、数…...

【Python爬虫案例教学】采集某网站壁纸,实现壁纸自由
前言 (。・∀・)ノ゙嗨 大家好,这里是小圆 现在开始每天都给大家 分享些关于python爬虫的案例教学 从最简单的开始 — 采集图片壁纸 今天就来扒拉这个优质的壁纸网站~ 网址 👇 顺便瞧一眼 这里的…...

波卡2022年第四季度报告
本文将介绍Messari最新发布的波卡Polkadot 2022年第四季度报告内容。 1 Messari已经发布关于波卡Polkadot最新的报告:显示了2022年第四季度的日活账户增加了64%,新用户增长49%。 2 Messari指出,波卡中继链在2022第四季度的环比增长令人印象…...
第一章:初始化react项目+antd+less
初始化react项目 我们首先使用react脚手架创建一个项目 Ant Design less creact-react-app中文文档 creact-react-app demo生产环境打包运行 当我们执行了 npm run build 打包后直接访问index.html 看效果白屏 这时候就需要安装一个serve包 npm install -g serve当我们安…...
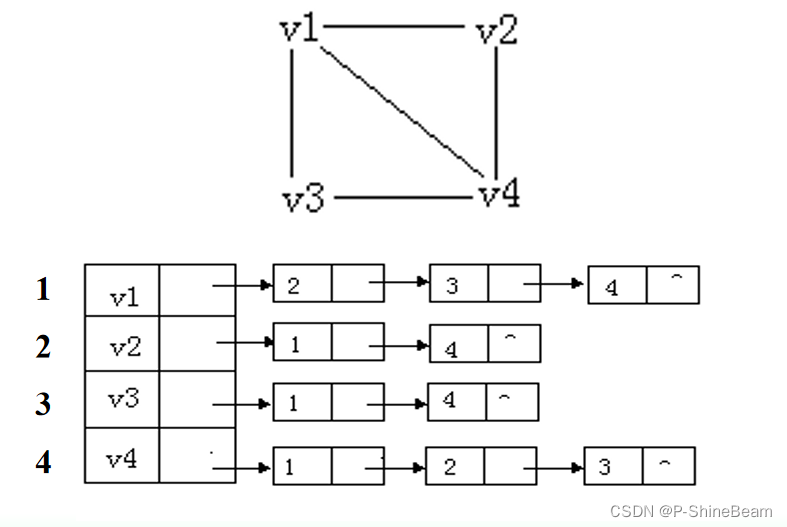
图的基本概念
1、图的概念 G(V,E) 图G由节点集合VV(G)和边集合EE(G)组成,其中V为非空有限集合。 集合V中的节点(node)用红色标出,通过集合E中黑色的边(edge)连接。 G的边:E中的每个顶点对&#x…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
