回溯算法章末总结
-
组合问题的特点
(1)ab=ba 选中a之后,就不再选了
(2)找出所有的组合 (长度可以不相等) -
组合问题模板

-
做回溯题步骤
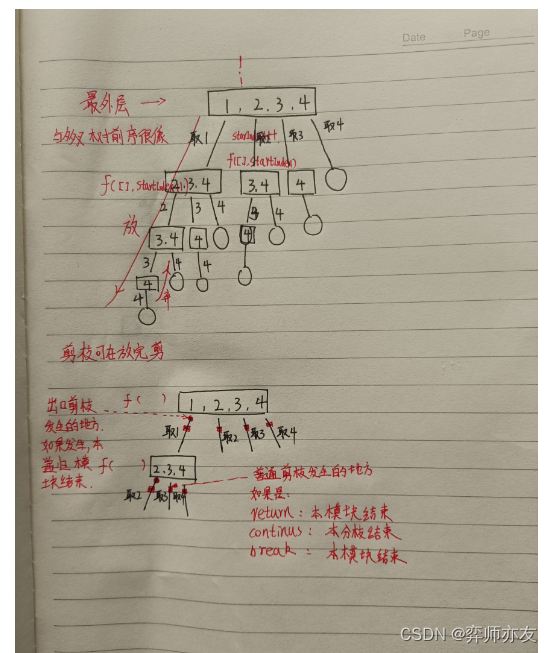
(0)判断问题类型
(1)树状图
(2)递归三部曲
(3)剪枝条件 -
组合问题中的纵横剪枝 ----> 216.组合总和III
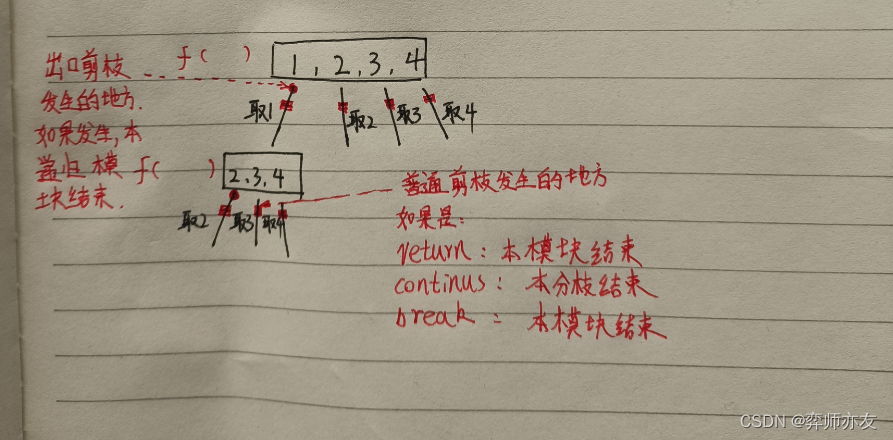
-
去重
(1)横向去重
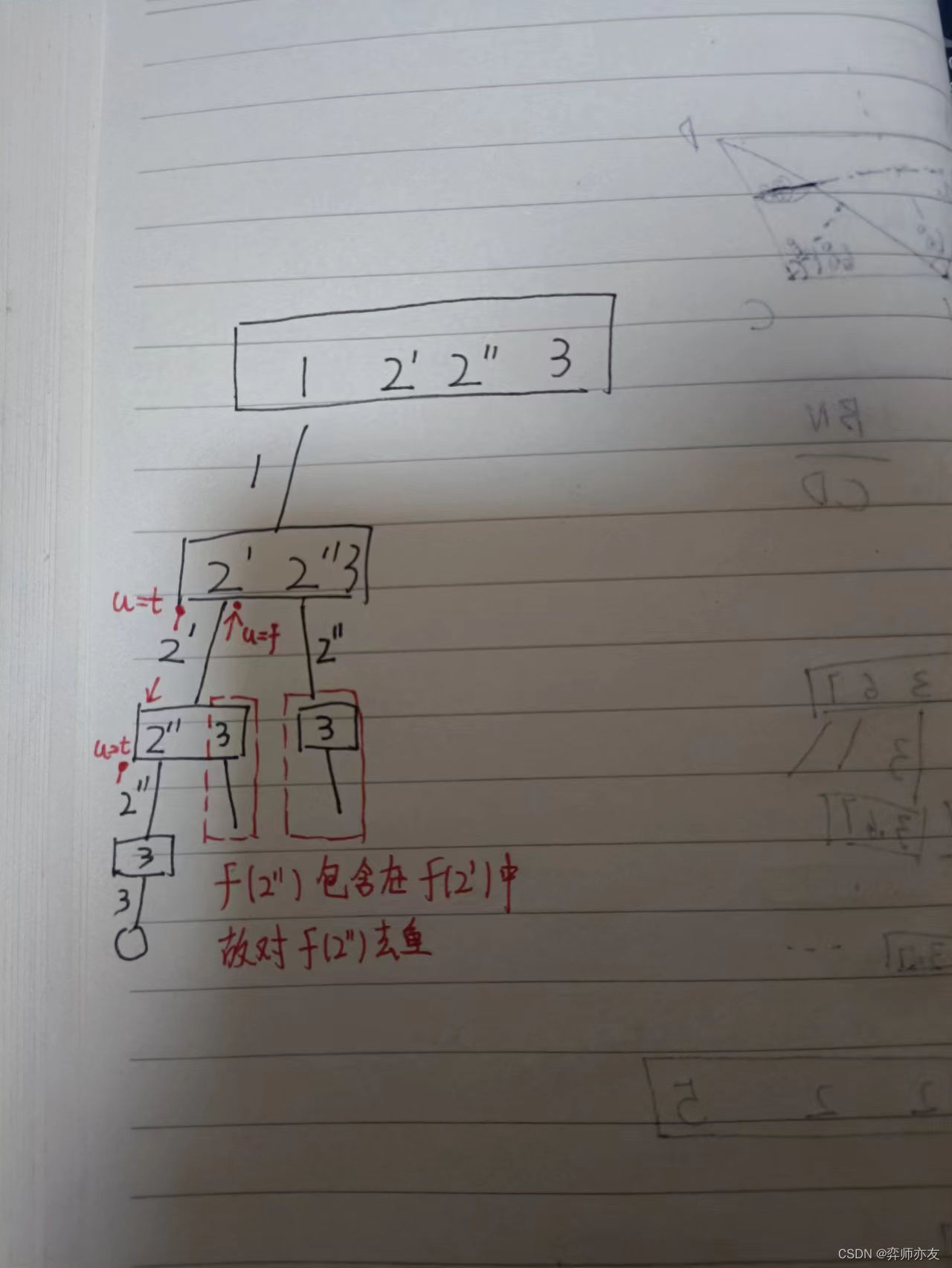
(2)set横向去重
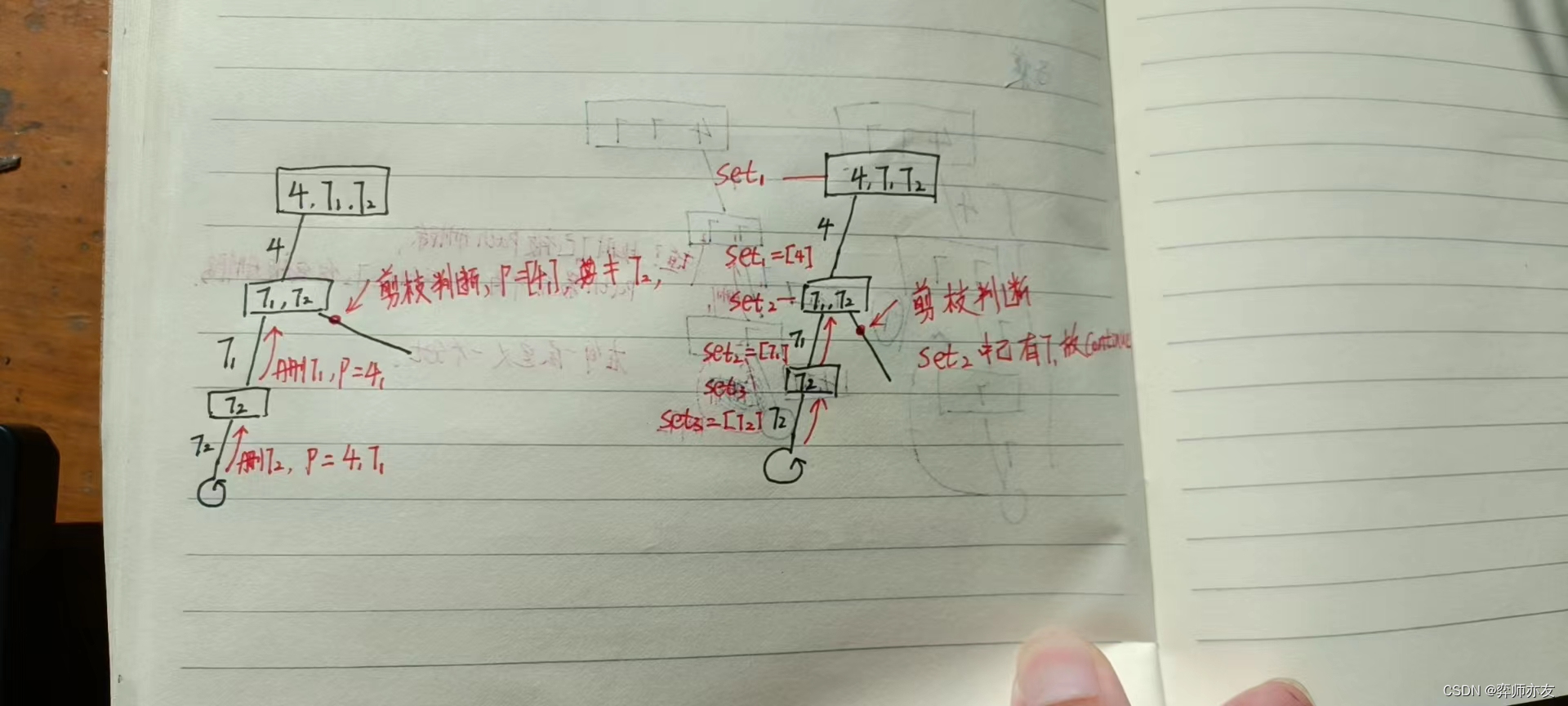
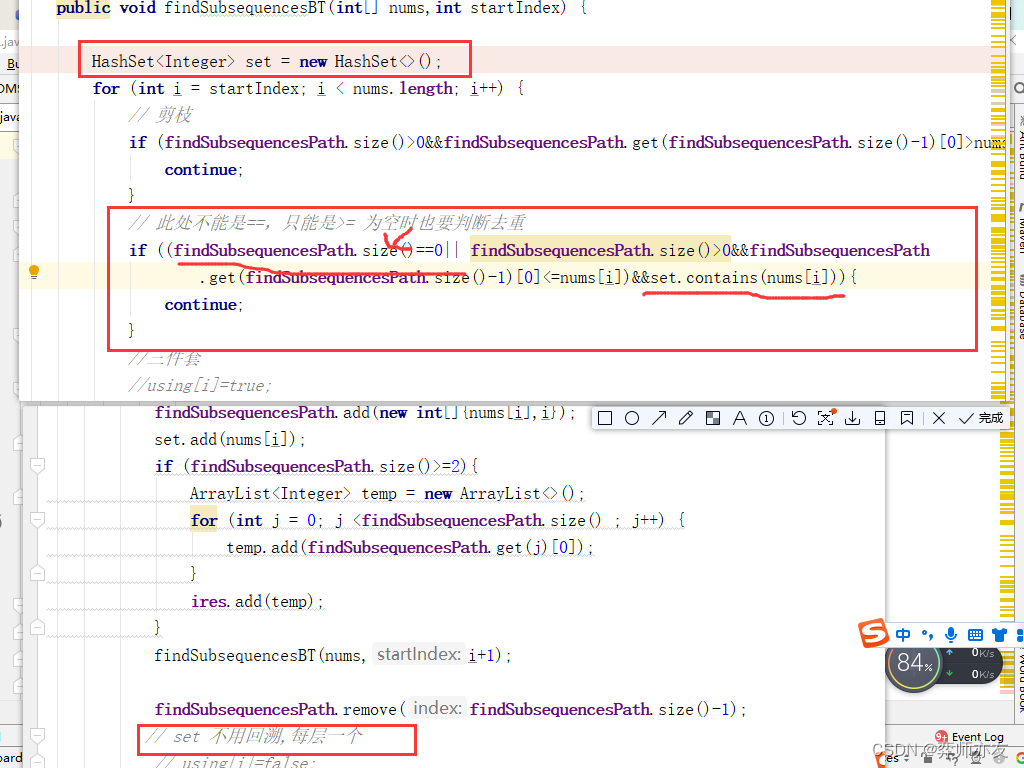
代码
public void findSubsequencesBT(int[] nums,int startIndex) {HashSet<Integer> set = new HashSet<>();for (int i = startIndex; i < nums.length; i++) {// 剪枝if (findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]>nums[i]){continue;}// 此处不能是==,只能是>= 为空时也要判断去重if ((findSubsequencesPath.size()==0||findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]<=nums[i])&&set.contains(nums[i])){continue;}//三件套//using[i]=true;findSubsequencesPath.add(new int[]{nums[i],i});set.add(nums[i]);if (findSubsequencesPath.size()>=2){ArrayList<Integer> temp = new ArrayList<>();for (int j = 0; j <findSubsequencesPath.size() ; j++) {temp.add(findSubsequencesPath.get(j)[0]);}ires.add(temp);}findSubsequencesBT(nums,i+1);findSubsequencesPath.remove(findSubsequencesPath.size()-1);// set 不用回溯,每层一个// using[i]=false;}}
关键
- 分割递归终止条件
分割常用的递归出口
(1)startIndex==数组长度
缺点: 如果是分割有段数要求,例如ip,可能分割很多段后才到递归出口,1.1.1.1.1.1.1 再判断,白白浪费性能。
改进:当已经分割三段时,第四段直接判断,这样可以剪掉部分,但是最后还是会一个一个试
public void restoreIpAddressesBT(String s,int startIndex) {if (startIndex==s.length()){if (restoreIpAddressesPath.size()==4){StringBuilder sb = new StringBuilder();for (String s1 : restoreIpAddressesPath) {sb.append(s1+".");}sb.delete(sb.length()-1,sb.length());slist.add(sb.toString());}return;}for (int i = startIndex; i <s.length() ; i++) {String substring = s.substring(startIndex, i + 1);// 剪枝// 如果已经有3个了,直接看剩下的能不能凑成第四个就行if (restoreIpAddressesPath.size()==3&&valIsValid(s.substring(startIndex))==-1){return; // 本层全不能用}if (valIsValid(substring)==-1){continue;}restoreIpAddressesPath.add(substring);restoreIpAddressesBT(s,i+1);restoreIpAddressesPath.remove(restoreIpAddressesPath.size()-1);}}
(2)如果有段数要求,直接用段数作为剪枝条件
if (restoreIpAddressesPath.size()==4){if (startIndex==s.length()){StringBuilder sb = new StringBuilder();for (String s1 : restoreIpAddressesPath) {sb.append(s1+".");}sb.delete(sb.length()-1,sb.length());slist.add(sb.toString());}return;}
这样只要到段数,就会判断,不会再 1.1.1.1.1.1.1这样分
题型
组合问题
每条从根出发的子路径是一个结果
- 传统组合问题 每一条子路径都是一种组合 —>● 77. 组合● 216.组合总和III
- 从筐中取球类型–>● 17.电话号码的字母组合
- 组合,元素不重,元素可重复取 39. 组合总和
- 组合,元素重复,结果不重,横向去重–> 40.组合总和II
子集问题
- 组合问题之子集问题,找到所有从根节点出发的子路径,包含【】
---->78.子集 - 组合问题之递增序列,本质是子集问题,使用set去重,注意第一层时path可能为空 491.递增子序列
分割
每条路径是一个结果
5. 标准分割 --> 131.分割回文串 ● 93.复原IP地址
排列
- 排列,借助used数组 46.全排列 47.全排列 II
递归树
-
传统组合
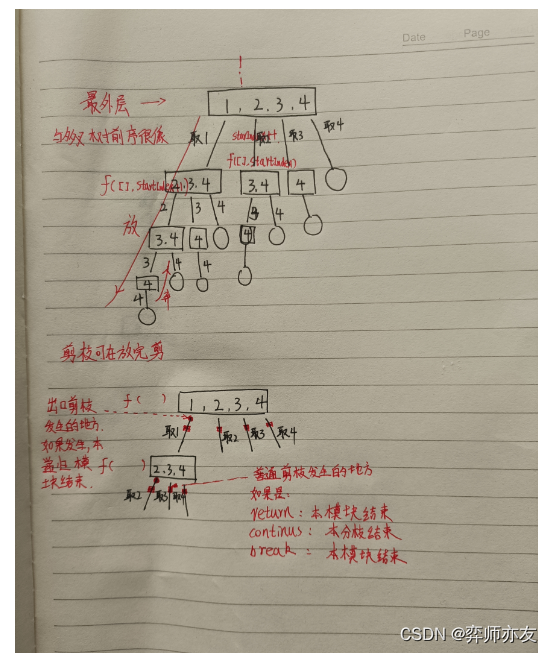
-
筐中取球
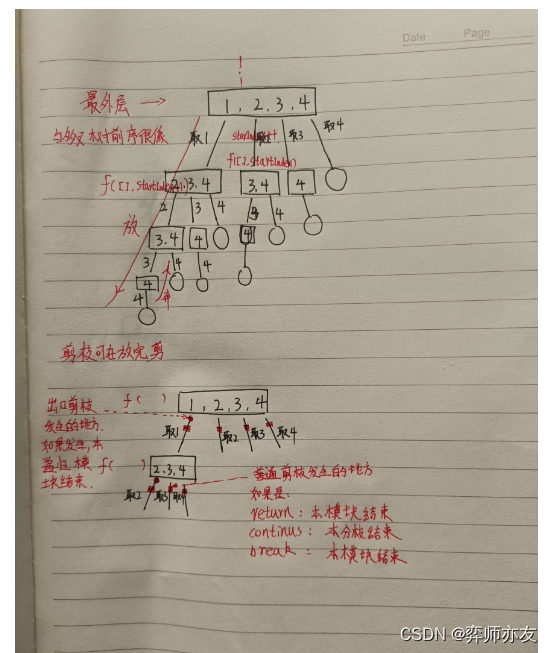
-
组合,每个元素可重复
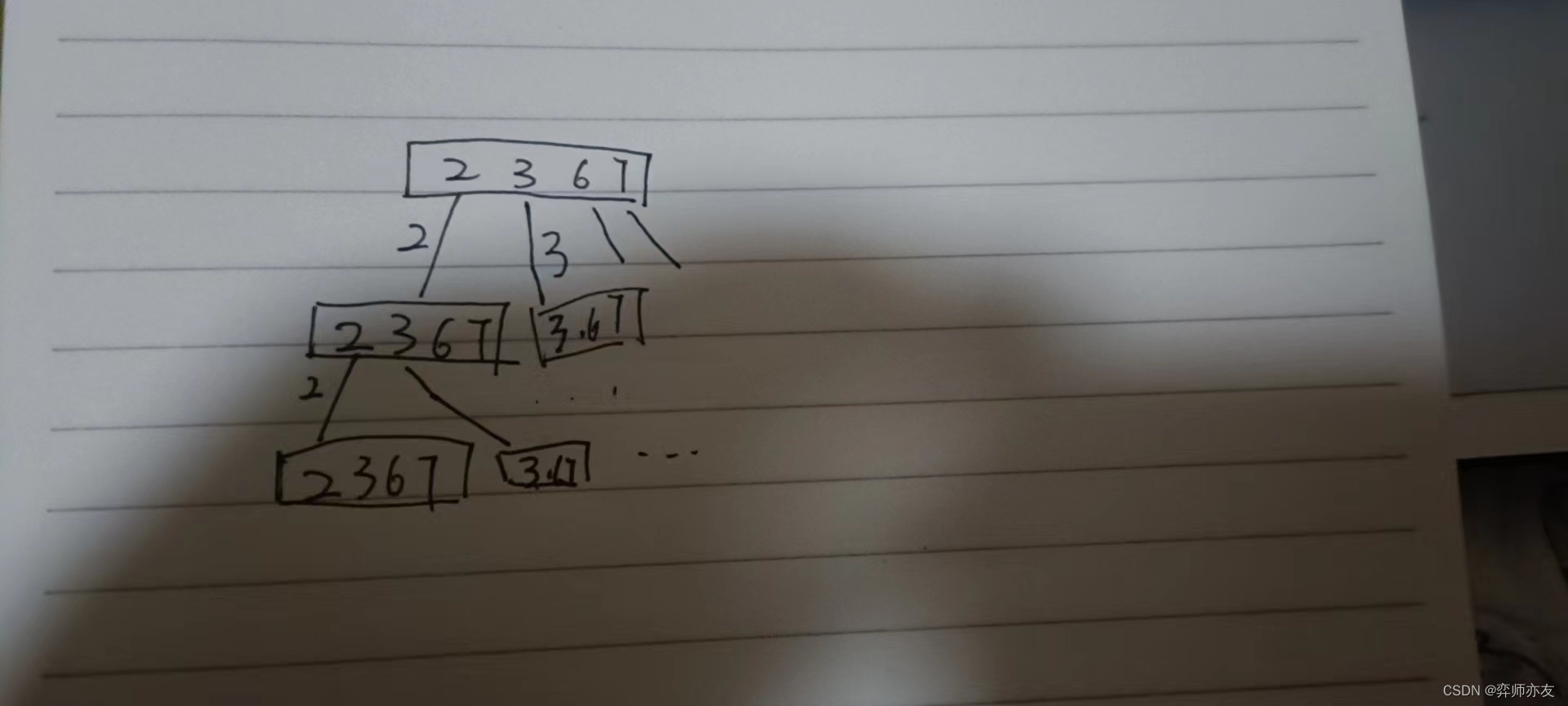
-
组合,元素重复,结果不重,横向去重
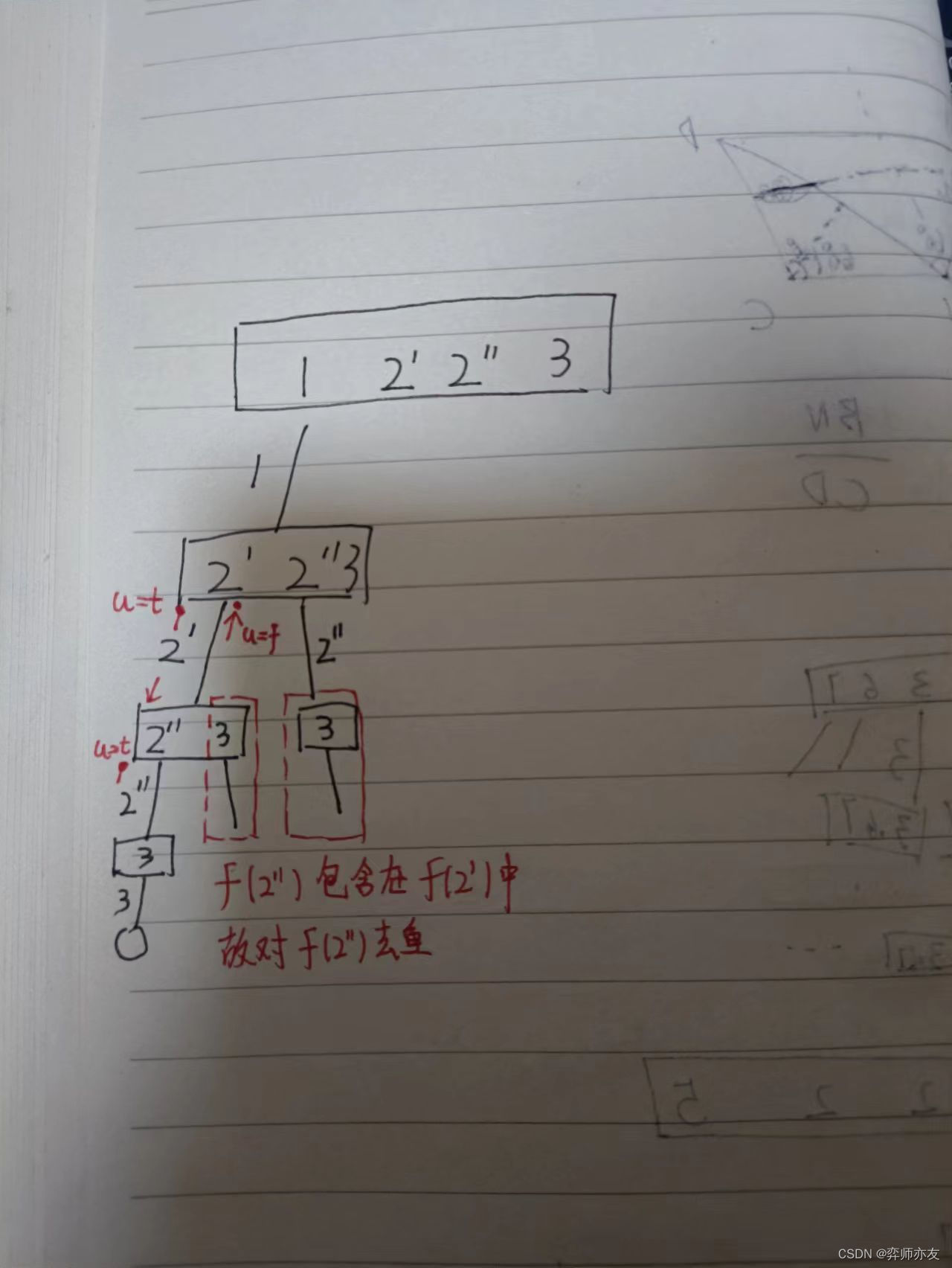
-
标准分割

(2)分割模板
// 131.分割回文串 public void partitionBT(String s,int startIndex) {if (startIndex==s.length()){sres.add(new ArrayList<>(spath));return;}// 引擎for (int i = startIndex; i <s.length() ; i++) {// 剪枝if (!isPalindrome(s,i,startIndex)){return;}spath.add(s.substring(i, startIndex + 1));partitionBT(s,i+1);spath.remove(spath.size()-1);// 本层下一个}}
(3)不同之处

6. 子集问题
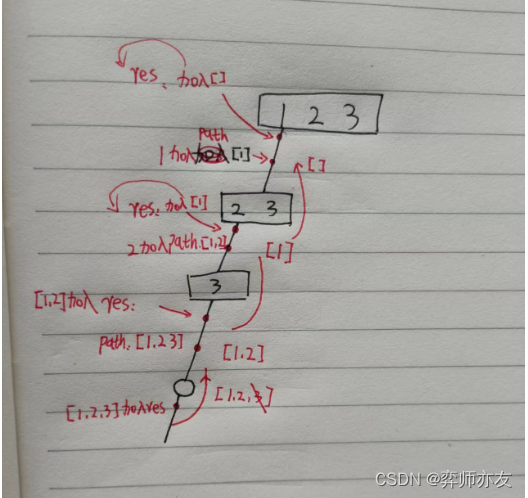
(2)子集问题模板
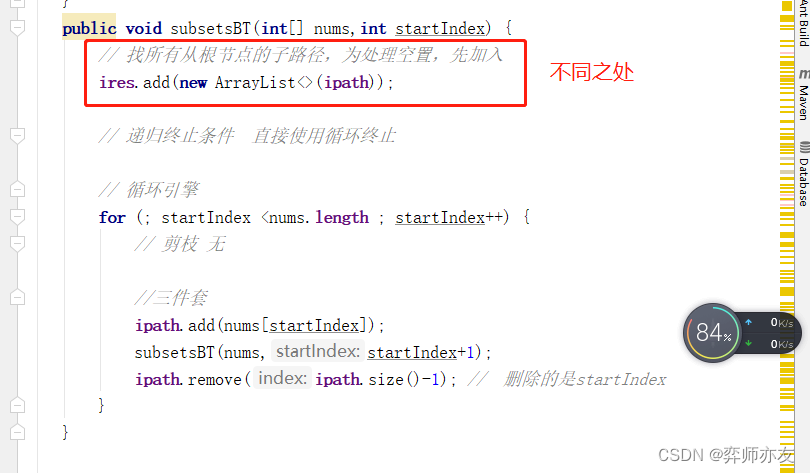
// 78. 子集public void subsetsBT(int[] nums,int startIndex) {// 找所有从根节点的子路径,为处理空置,先加入ires.add(new ArrayList<>(ipath));// 递归终止条件 直接使用循环终止// 循环引擎for (; startIndex <nums.length ; startIndex++) {// 剪枝 无//三件套ipath.add(nums[startIndex]);subsetsBT(nums,startIndex+1);ipath.remove(ipath.size()-1); // 删除的是startIndex}}
(3)不同之处
7. 递增序列问题

代码
public void findSubsequencesBT(int[] nums,int startIndex) {HashSet<Integer> set = new HashSet<>();for (int i = startIndex; i < nums.length; i++) {// 剪枝if (findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]>nums[i]){continue;}// 此处不能是==,只能是>= 为空时也要判断去重if ((findSubsequencesPath.size()==0||findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]<=nums[i])&&set.contains(nums[i])){continue;}//三件套//using[i]=true;findSubsequencesPath.add(new int[]{nums[i],i});set.add(nums[i]);if (findSubsequencesPath.size()>=2){ArrayList<Integer> temp = new ArrayList<>();for (int j = 0; j <findSubsequencesPath.size() ; j++) {temp.add(findSubsequencesPath.get(j)[0]);}ires.add(temp);}findSubsequencesBT(nums,i+1);findSubsequencesPath.remove(findSubsequencesPath.size()-1);// set 不用回溯,每层一个// using[i]=false;}}
关键

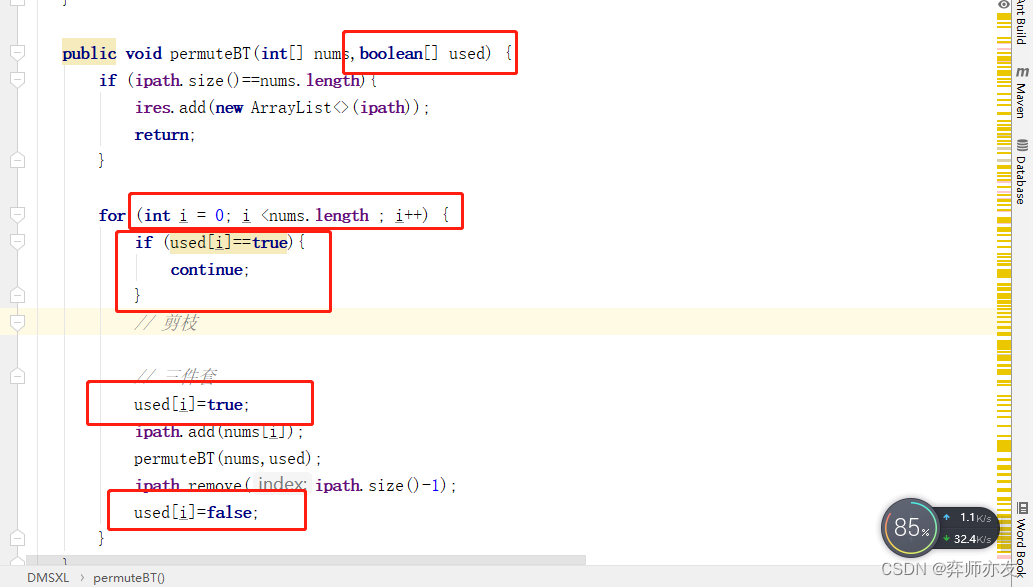
8. 排列
public void permuteBT(int[] nums,boolean[] used) {if (ipath.size()==nums.length){ires.add(new ArrayList<>(ipath));return;}for (int i = 0; i <nums.length ; i++) {if (used[i]==true){continue;}// 剪枝// 三件套used[i]=true;ipath.add(nums[i]);permuteBT(nums,used);ipath.remove(ipath.size()-1);used[i]=false;}}
相关文章:

回溯算法章末总结
组合问题的特点 (1)abba 选中a之后,就不再选了 (2)找出所有的组合 (长度可以不相等) 组合问题模板 做回溯题步骤 (0)判断问题类型 (1)树状图 …...

【SpringBoot】为异步任务规划线程池
一、线程池的作用 防止资源占用无限的扩张调用过程省去资源的创建和销毁所占用的时间 在上一节中,我们的一个异步任务打开了一个线程,完成后销毁。在高并发环境下,不断的分配新资源,可能导致系统资源耗尽。所以为了避免这个问题…...
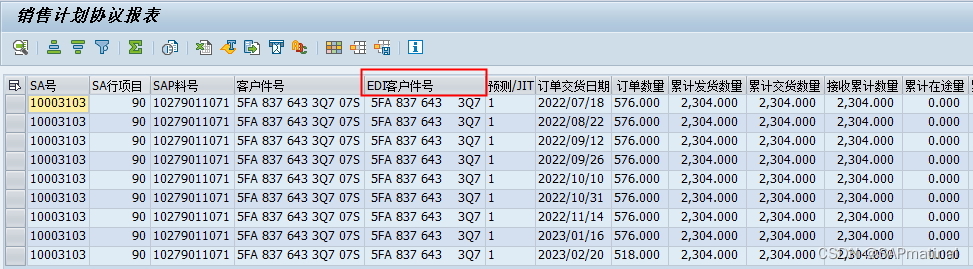
SAP ABAP 输出结果带有空格
方法一: 字段内容前增加空格,需使用全角空格,使用半角空格时,ALV显示无效,空格无法显示, 全角与半角的切换方法:shift空格切换, 如下的标记部分,要想通过ALV显示空格&…...

Opengl ES之踩坑记
前因 最近在尝试使用Opengl ES实现一些LUT滤镜效果,在实现这些滤镜效果的时候遇到一些兼容性的坑,踩过这些坑后我希望把这几个坑分享给读者朋友们, 希望同在学习Opengl ES的朋友们能少走弯路。 关于LUT滤镜相关的介绍,也是这个O…...
设计模式第六讲:责任链模式和迭代器模式详解
一. 责任链模式1. 背景在现实生活中,常常会出现这样的事例:一个请求有多个对象可以处理,但每个对象的处理条件或权限不同。例如,公司员工请假,可批假的领导有部门负责人、副总经理、总经理等,但每个领导能批…...
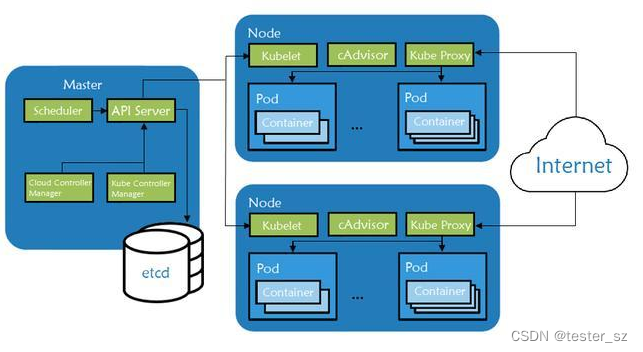
K8s 架构简介(一)
一、前言 在开始学习K8s之前,让我们对容器有一个基本的了解 1.1 什么是容器 一个容器镜像是一个可运行的软件包,其中包含了一个完整的可执行程序,包括代码和运行时需要应用、系统库和全部重要设置的默认值。 通过将应用程序本身ÿ…...
xshell6运行报错:由于找不到mfc110u.dll、MSVCR110.dll无法继续执行代码
今天给大家分享一下我刚装完系统遇到得问题,由于新盟的罗建雨【胡巴】老师帮我给电脑加了固态,又重装了系统,因此电脑里面得所有软件需要重装,在我重装的过程中遇到了一个小问题给大家分享一下,如果大家以后遇到也方便解决。 问题: 安装Xshell时电脑系统报错:“由于找…...
Baklib知识库管理平台,协助组织提升知识管理水平
随着信息时代和知识经济时代的到来,企业内部信息资料繁多冗杂,知识管理逐渐成为各大企业的重要工作之一,企业管理者无不感受到巨大的压力,怎么样将知识进行有效的管理,成为一个难点,并且随着信息不断的更迭…...
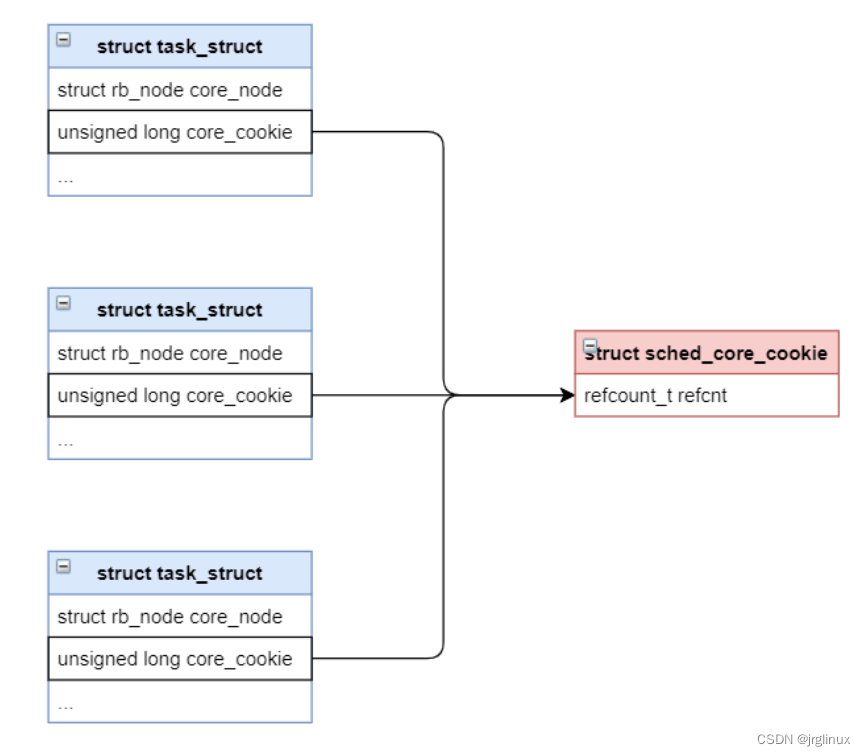
一文搞懂core-scheduling核心机制
cookie的原理借助于unsigned long型,和refcount_t引用计数器。 32位64位char *4字节8字节unsigned long4字节8字节 数据结构修改 首先看看实现core scheduling功能对数据结构有哪些修改 task_struct struct task_struct{struct rb_node core_node;unsigned long…...

IP地址在金融行业有哪些应用?
中国加入WTO以来经济得到迅速发展,金融行业随着经济发展体系越来越完善。随着西方金融公司和理念的加入中国金融行业开始多样化发展。金融行业在快速发展的同时也引发了许多弊端。如何维护挖掘客户更大需求?如何获取更多优质客户?如何提升网络…...
GT-suite v2016解决许可证过期问题(附新版liscense下载地址)
安装GT-suite v2016时遇到了如图报错的问题。当时的报错找不到了,下图是贴吧相同问题的报错图。 为了解决问题,先根据某网友的如下答复操作: 添加环境变量后仍然有相同报错。 看来需要寻找其他方法。 再尝试着卸载GT-suite v2016,…...

小红书商业笔记与普通笔记区别是什么?小红书笔记有哪几种
主攻单一平台,如何迅速打造爆文。针对软文发布类别的选择,小红书商业笔记与普通笔记区别究竟是什么,今天为大家带来的详细分析,告诉你该如何用最少的成本,做出“爆文”。1、小红书的笔记类型我们都知道,小红…...
DataWhale-统计学习方法打卡Task01
学习教材《统计学习方法(第二版)》李航 统计学习方法(第2版) by...李航 (z-lib.org).pdf https://www.aliyundrive.com/s/maJZ6M9hrTe 点击链接保存,或者复制本段内容,打开「阿里云盘」APP ,无…...
Java面试——Spring 事务
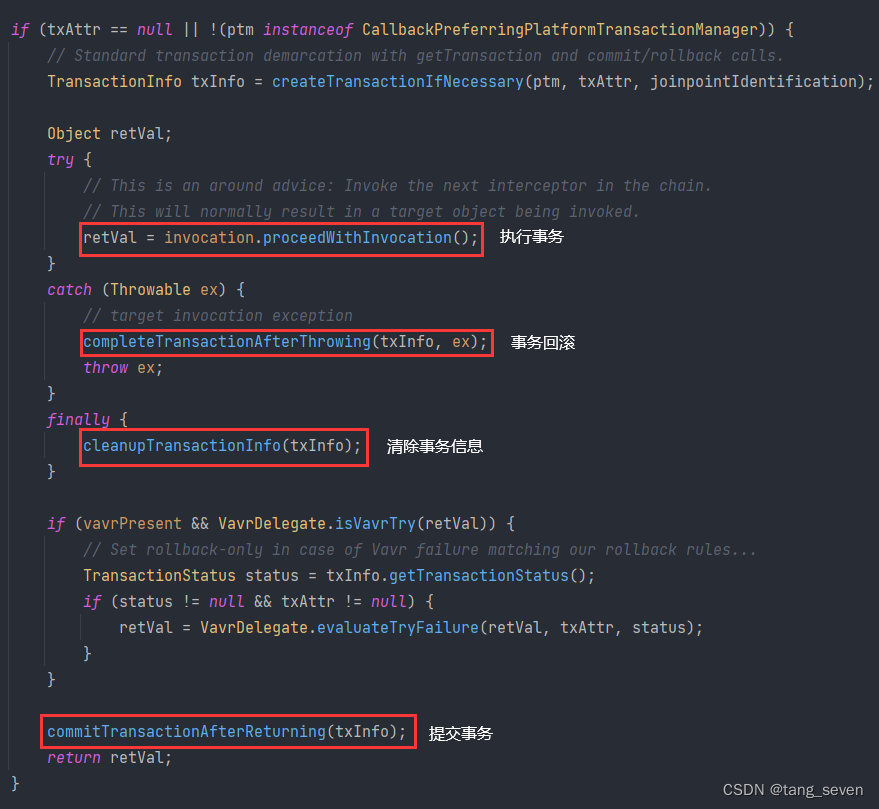
目录 1.什么是Spring 事务 2.Spring 事务的开启方式 3.Spring事务的实现方式/原理 4.事务传播机制 5.事务隔离级别 6.事务失效的原因 1.什么是Spring 事务 事务在逻辑上是一组操作,要么执行,要不都不执行。 如下: Begin; insert into…...
Python语言零基础入门教程(十九)
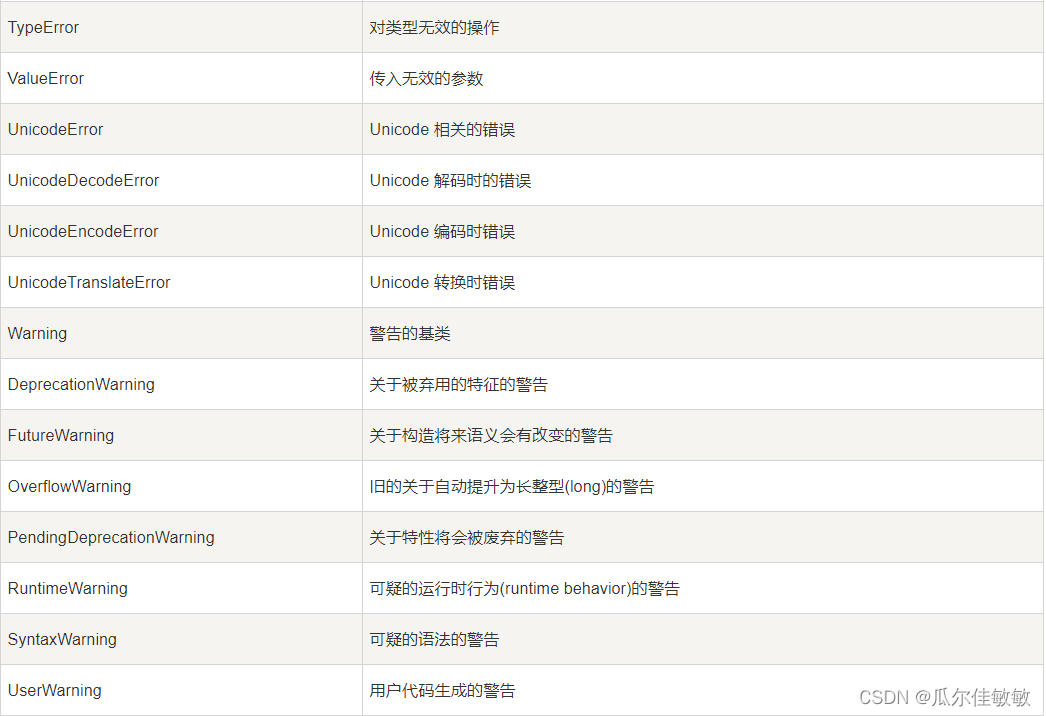
Python 异常处理 python提供了两个非常重要的功能来处理python程序在运行中出现的异常和错误。你可以使用该功能来调试python程序。 1、异常处理 2、断言(Assertions) python标准异常 什么是异常? 异常即是一个事件,该事件会在程序执行过程中发生&…...
重生之我是赏金猎人-SRC漏洞挖掘(一)-某SRC测试系统无脑Getshell
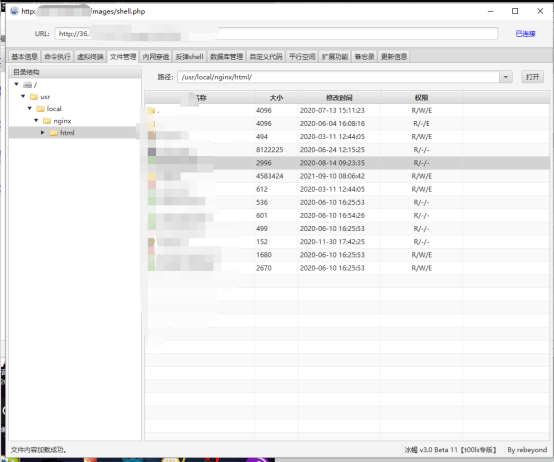
0x01 前言 https://github.com/J0o1ey/BountyHunterInChina 欢迎大佬们点个star 0x02 资产收集到脆弱系统 在某src挖掘过程中,本人通过ssl证书对域名资产进行了收集,通过计算域名对应ip段的权重 整理出其C段资产,进行了批量目录扫描 查看…...

Sciter 结合 PReact 实现组件公共逻辑抽离
Sciter 结合 PReact 实现组件公共逻辑抽离 下面例子是获取鼠标移动位置,将这部分逻辑进行抽离 一、使用高阶组件抽离公共逻辑 import {Component } from ./preact.js; export const HOCFactory = (Component) => {class HOC...
OpenTracing协议规范链接
一、官网链接 OpenTracing specificationhttps://opentracing.io/specification/不过目前OpenTracing项目已归档,不再维护。需要参考OpenTelemetry官网链接 Migrating from OpenTracing | OpenTelemetryBackward compatibility with OpenTracing has been a prior…...
金三银四面试必看,自动化测试如何解决日志问题
前言 前几天在员群里,有同学问了一个自动化测试实践中遇到的问题: 持续集成的自动化用例很多,测试环境日志level为debug,日志量大概40G/每天,定位问题时日志查询很慢,该怎么解决? 这个问题可…...
微信怎么开小店?【企业商家微信开店】
企业商家入局微信做营销已经是经营规划中必须做的一件事了,对于企业商家来说,最简单直接的方式就是开一个微信小店,然后通过自己宣传推广来在微信小店中成商品。那么企业商家在微信怎么开小店呢?下面内容分享给想在微信开店的企业…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
