实现光线追踪重投影的方法
光线追踪重投影方法
重投影这项技术一般用于时间性帧复用技术上,例如TAA(Temporal Anti-Aliasing)反走样或者抗锯齿技术。读这篇文章最好先对TAA这类技术的算法流程有了解。
1.TAA抗锯齿技术简介
先简单介绍下TAA抗锯齿的原理,在游戏中,当前渲染一帧画面的单独拎出来看,是有锯齿的(物体边缘有狗牙),而TAA则将历史帧作为抗锯齿的参考数据(可以一帧也可以多帧)。为当前帧的一个像素找到它在历史帧中对应的那个像素,做个权重混合。如果用多个历史帧的话,那么越久远的帧在混合中使用的权重越低。
大致的原理图如下:

所以TAA技术的重点之一就是上图那根红色箭头,如何为当前像素找到它在上一帧中对应的位置。实现这个红色箭头的就是重投影技术。
2.重投影技术的简介
重投影技术,将当前像素进行投影,分为两种:
- 反向重投影:从当前像素反向寻找其在历史帧中的位置。
- 前向重投影:从历史像素前向寻找其在当前帧中的位置。
我认为区分清楚这两种方向不同的方法非常关键和重要。
TAA抗锯齿技术这类时间性复用技术,几乎只用于光栅渲染,很少在光线追踪中用到。并不是光线追踪渲染的图无锯齿,而是光线追踪渲染无法提供光栅渲染在重投影技术中所需要的数据,因此TAA技术无法或者很难直接从光栅渲染中套用在光线追踪渲染中。
重投影在光栅渲染中已有成熟的方法,但是在光线追踪中的相关研究较少,缺乏通用的方法。光栅渲染做重投影通常用的是反向重投影的方法。例如使用运动矢量(Motion Vecter)方法或者通过投影矩阵反推的方法。
但是运动矢量和投影矩阵方法都是用到光栅渲染过程中可以天然产生的数据,而光线追踪渲染的方法又大大不同,这些数据都没法在渲染过程中天然获得。
3. 光线追踪前向重投影方法
因为接触到查阅到的大多都是反向重投影的思路,所以我想了很久为光线追踪做重投影的路子,都觉得太绕太复杂。
后面读文献才知道还有前向重投影这个方向。我就想反过来从历史像素推出它大概会在当前帧跑到哪里行不行。答案是可以的,前向重投影的思路能够直接使用光线追踪过程中产生的数据。
先假设这个光线追踪场景:场景中物体都是静止不动的,前后帧只有摄影机是运动的,重投影只用到一帧历史帧。
原理图:

具体方法流程:
-
该重投影方法需要缓存历史帧碰撞点坐标。
-
遍历历史像素时,首先取出像素对应的历史碰撞点坐标,利用当前摄像机参数将该坐标从世界坐标系变换到当前帧的摄像机坐标系中。
-
然后利用相似三角形理论将该历史碰撞点的三维坐标变换为当前帧中的 UV 坐标,请看下图。

-
在摄像机坐标系中将摄像机与屏幕像素平面和历史光线碰撞点连接成相似三角形,再利用摄影机到像素平面的距离求该碰撞点在像素屏幕中的x 和y 坐标(即当前帧的UV坐标)。
-
接着将 UV 坐标转换为 NDC 标准设备坐标,再根据当前窗口尺寸计算得到光栅坐标。该光栅坐标即历史像素映射到目标帧中的像素坐标,若映射结果超出目标帧的像素范围则弃用;最后将历史像素颜色值存入重投影缓存中,用于与当前渲染帧像素做加权混合。
算法流程图:

效果:
能够实现光线追踪的重投影算法,那TAA抗锯齿当然能做。我觉得有一块更适合用在光线追踪上的就是降噪,光线追踪采样数低的时候噪点非常严重,结果重投影技术去研究降噪技术,是一种省时间省性能的方法。
下图是我做的对光线追踪采样光线数量只有一条的时候,用了上面重投影技术做的时间性降噪方法,前后对比还是比较明显的。

因为并没有做额外帧的渲染,所以性能额外消耗很少。不过采样数只有1,也是尽力了,把采样次数提高一点的话,降噪效果也挺好,只是1的时候差异很明显。
4.讨论
上面的方法也是限定了场景的:场景中物体都是静止不动的,前后帧只有摄影机是运动的,重投影只用到一帧历史帧。
如果场景中物体会发生变换的话,我没有继续研究下去,不过我的想法是,现在方法是只有摄像机在运动,如果物体发生变换的话,那就是与摄像机发生相对运动。那就记录物体的变换矩阵,把历史帧物体的碰撞点坐标变换到当前帧的新三维坐标,再使用上面介绍的算法去计算历史像素其在当前帧中的目标像素点。
有其他光线追踪重投影想法的,或者我的算法有啥缺点改进的,都欢迎找我交流。
相关文章:

实现光线追踪重投影的方法
光线追踪重投影方法 重投影这项技术一般用于时间性帧复用技术上,例如TAA(Temporal Anti-Aliasing)反走样或者抗锯齿技术。读这篇文章最好先对TAA这类技术的算法流程有了解。 1.TAA抗锯齿技术简介 先简单介绍下TAA抗锯齿的原理,在游戏中,当前…...

Hyperbolic Representation Learning for CV
Contents Hyperbolic geometry[CVPR 2020] Hyperbolic visual embedding learning for zero-shot recognitionIntroductionApproachHyperbolic Label Embedding LearningHyperbolic Image Embedding LearningExperiment[CVPR 2020] Hyperbolic Image EmbeddingsIntroduction...
In Context Learning 相关分享
个人知乎详见 https://zhuanlan.zhihu.com/p/603650082/edit 1. 前言 随着大模型(GPT3,Instruction GPT,ChatGPT)的横空出世,如何更高效地提示大模型也成了学术界与工业界的关注,因此In-context learning…...
【前端笔试题一】:解析url路径中的query参数
前言 本文记录下在笔试过程中的前端笔试编程题目,会持续更新 1. 题目: 解析 url 路径中的 query 参数,比如:‘http://building/#/skeleton?serialNumber2023020818332821073&jobNo210347&target%7B%22a%22%3A%22b%22%2C…...
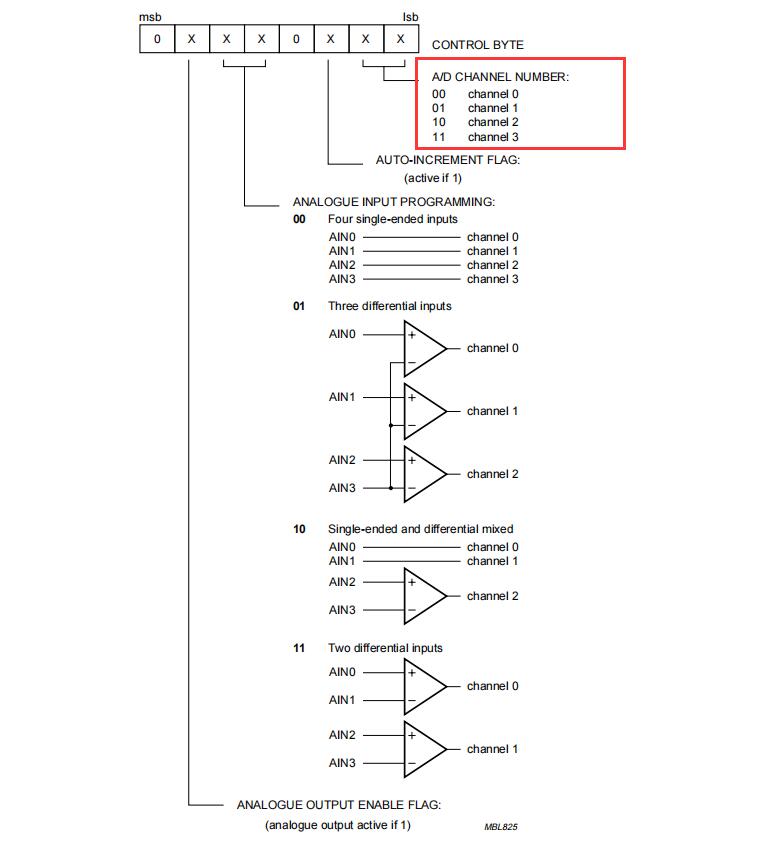
K_A12_001 基于STM32等单片机采集火光火焰传感参数串口与OLED0.96双显示
K_A12_001 基于STM32等单片机采集火光火焰传感参数串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:四、部分代码说明1、接线引脚定义1.1、STC89C52RC火光火焰模块1.2、STM32F103C8T6火光火焰模块五、基础知识学习与相…...
Java基础42 枚举与注解
枚举与注解一、枚举(enumeration)1.1 自定义类实现枚举1.2 enum关键字实现枚举1.2.1 enum的注意事项1.2.2 enum的使用练习1.2.3 enum的常用方法1.2.4 enum的使用细节及注意事项1.2.5 enum练习二、注解(Annotation)2.1 Override&am…...

shell的变量和引用
文章目录二、变量和引用2.1 什么是变量2.2变量的命名2.3 变量的类型2.3.1 根据数据类型分类2.3.2 根据作用域分类2.4 变量的定义2.5 shell中的引用2.6 变量的运算练习:二、变量和引用 在程序设计语言中,变量是一个非常重要的概念。也是初学者在进行Shel…...

基于PHP的招聘网站
摘要在Internet高速发展的今天,我们生活的各个领域都涉及到计算机的应用,其中包括在线招聘的网络应用,在外国在线招聘已经是很普遍的方式,不过国内的在线招聘可能还处于起步阶段。招聘网站具有招聘信息功能的双向选择,…...
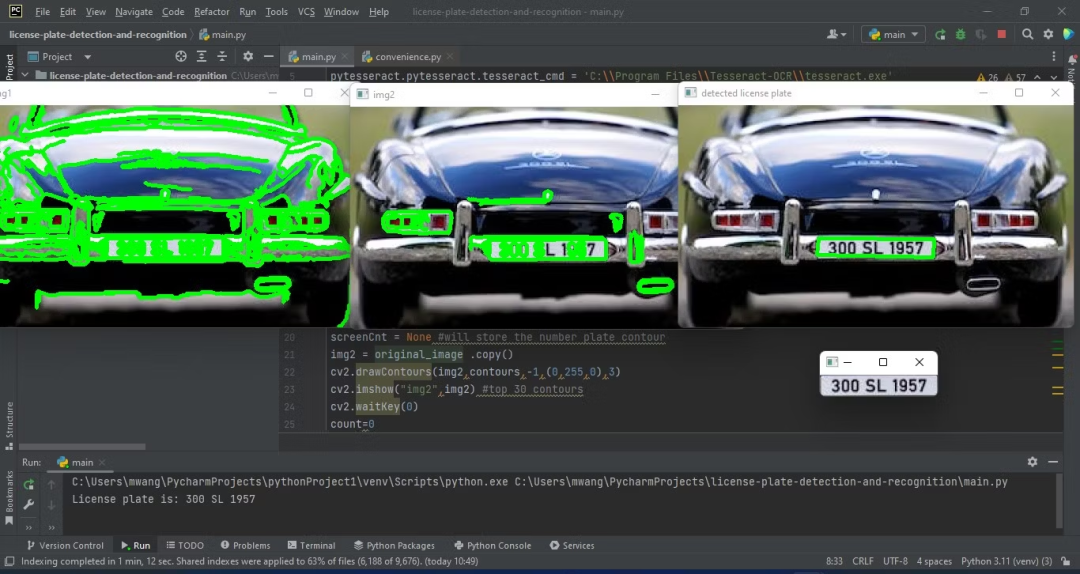
轻松使用 Python 检测和识别车牌(附代码)
车牌检测与识别技术用途广泛,可以用于道路系统、无票停车场、车辆门禁等。这项技术结合了计算机视觉和人工智能。 本文将使用Python创建一个车牌检测和识别程序。该程序对输入图像进行处理,检测和识别车牌,最后显示车牌字符,作为…...
DVWA—CSRF-Medium跨站请求伪造中级
注意: 1、这里对XSS(Stored)关卡不熟悉的可以从这里去看http://t.csdn.cn/ggQDK 2、把难度设置成 Medium 一、这一关同样我们需要埋下伏笔,诱使用户点击来提交,首先从XSS(Stored)入手。 注意:在前面介绍…...
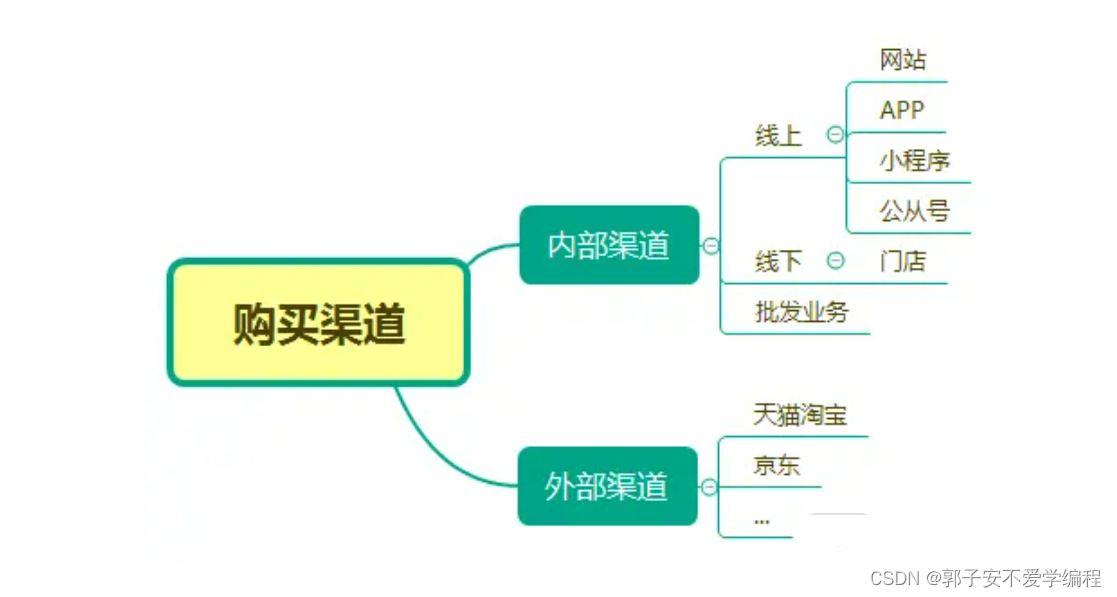
【电商】后台订单生成
结合商品流转的电商系列介绍了一些了,商品已经采购入库、价格税率设置好了、活动及相关模板也已经准备完毕,下面就应该上架销售了,现在接着聊下订单的生成。 订单从产生到最终的关闭需要经历很多的环节,订单也是电商系统的核心数据…...

作为公司,这个5款在线软件工具赶紧安利起来!
2023年了 ,您的企业还没使用在线软件工具吗?自从用了在线工具之后,感觉打开了新办公世界的大门,效率蹭蹭蹭地往上涨啊。对于喜欢追求效率和便捷的我来说,在线实在是太棒了!今天安利几个非常不错的在线软件工…...

面试(七)为什么一般希望将析构函数定义为虚函数
class B { public:~B() // 基类析构函数不为虚函数{cout << "B::~B()" << endl;} };class D : public B { public:~D(){cout << "D::~D()" << endl;} };void Test(B* t) {delete t;t nullptr; }int main() {B *pb new B;Test…...

MySQL必会四大函数-时间函数
一、时间日期获取函数 获取当前日期(date)函数:curdate() mysql> select curdate(); 2023-02-09 获取当前时间(time)函数:curtime() select curtime(); 08:49:27 获取当前时间戳(date &…...
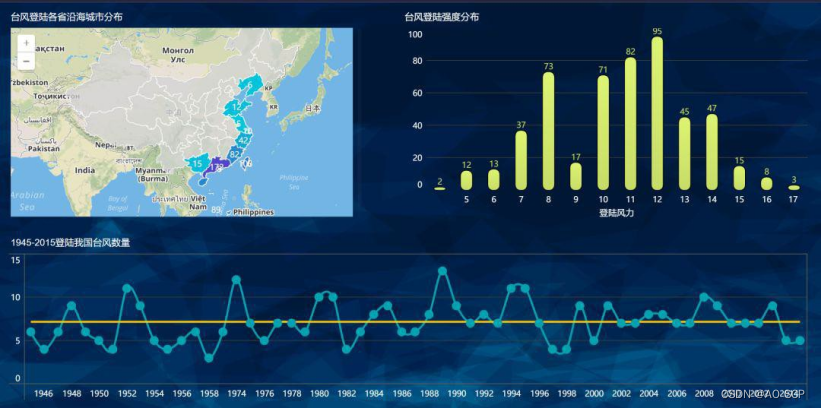
震惊!邻桌的程序猿做可视化报告竟然比我还快,带着好奇心我打开了他的电脑,发现惊天秘密,原因竟是...
其实,本文就是想分享一个做可视化的捷径! 制作可视化的方式有千千万。 Excel 控若能轻车熟路驾驭 VBA,能玩出各种花来,再不济借助图表插件外援也能秒杀一众小白选 手。 会编程的,Echarts 几十行代码,分分…...

mathtype7与word冲突,无法安装,不显示工具栏的问题解决
首先无法安装,或安装出错时,要清理注册表防止以后再次出现该问题,以此记录留作备份。打开注册表的方法是键盘winr键同时按(win就是Alt旁边像窗户图标的键),正常的话会跳出一个叫“运行”的家伙,…...

IBM AIX 升级Openssh 实现篇(编译安装)
升级成功佐证 !!!本文所有内容仅作参考,请在测试环境中具体测试完毕后才能应用于生产环境!!! [1]备份和恢复方案 开启telnet 服务,防止ssh 掉线后无法重连维护。在修复漏洞后关闭telnet。 备份该服务相关的所有文件,以便恢复。 root@TEST:/etc# vi inetd.conf #ftp…...
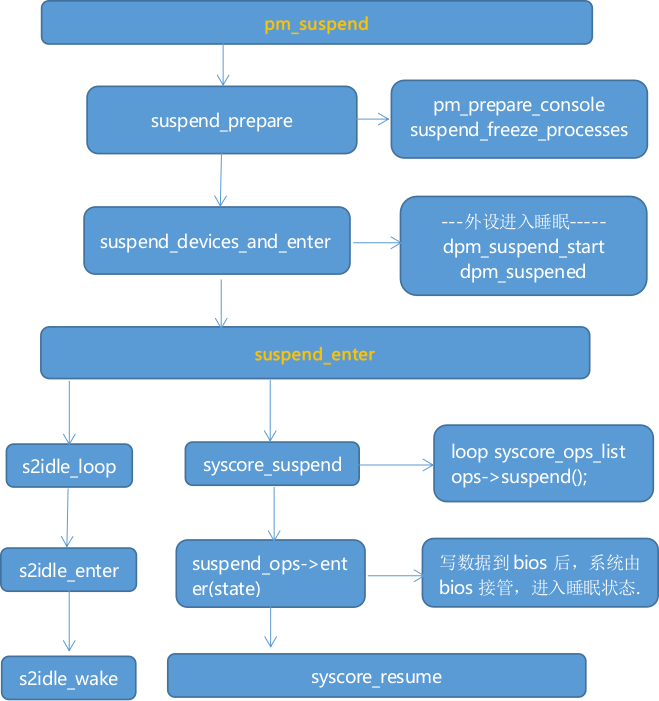
linux的睡眠框架及实现
睡眠 4 种模式:S2I (Suspend-to-Idle): 挂起系统,IO进入低功耗模式。需配置CONFIG_SUSPEND。Standby:执行S2I后,把AP (nonboot CPU) 离线。除了CONFIG_SUSPEND的支持外,还需要向suspend子系统注册ÿ…...
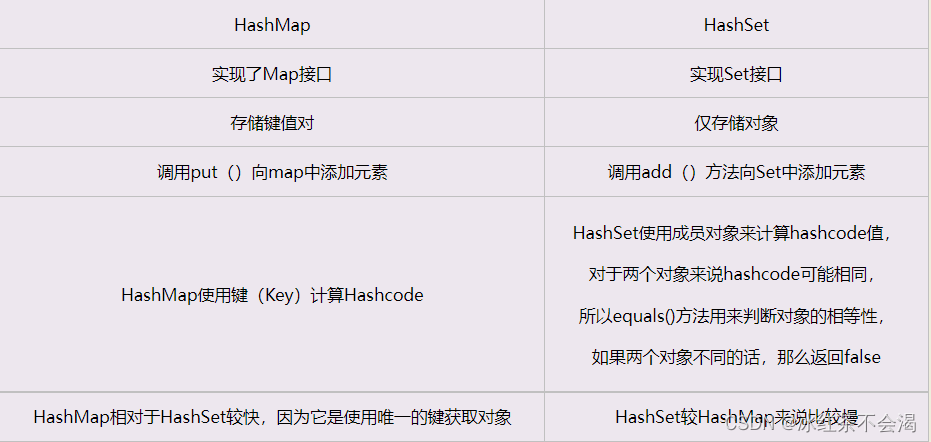
Java面试知识点
工作也有好些年了,从刚毕业到前几年看过无数的面试题,总想着自己写一个面试总结,随着自我认识的变化,一些知识点的理解也越来越不一样了。写下来温故而知新。很多问题可能别人也总结过,但是答案不尽相同,如…...

PTA Advanced 1159 Structure of a Binary Tree C++
目录 题目 Input Specification: Output Specification: Sample Input: Sample Output: 思路 代码 题目 Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, a binary tree can be un…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
