「4」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
第四章 向量组的线性相关性
&2)向量组的线性相关性
&3)向量组的秩
&4)线性方程组的解的结构
第四章 向量组的线性相关性
&2)向量组的线性相关性
&3)向量组的秩
&4)线性方程组的解的结构
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:
)
「4」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 第四章 向量组的线性相关性 &2)向量组的线性相关性 &3)向…...
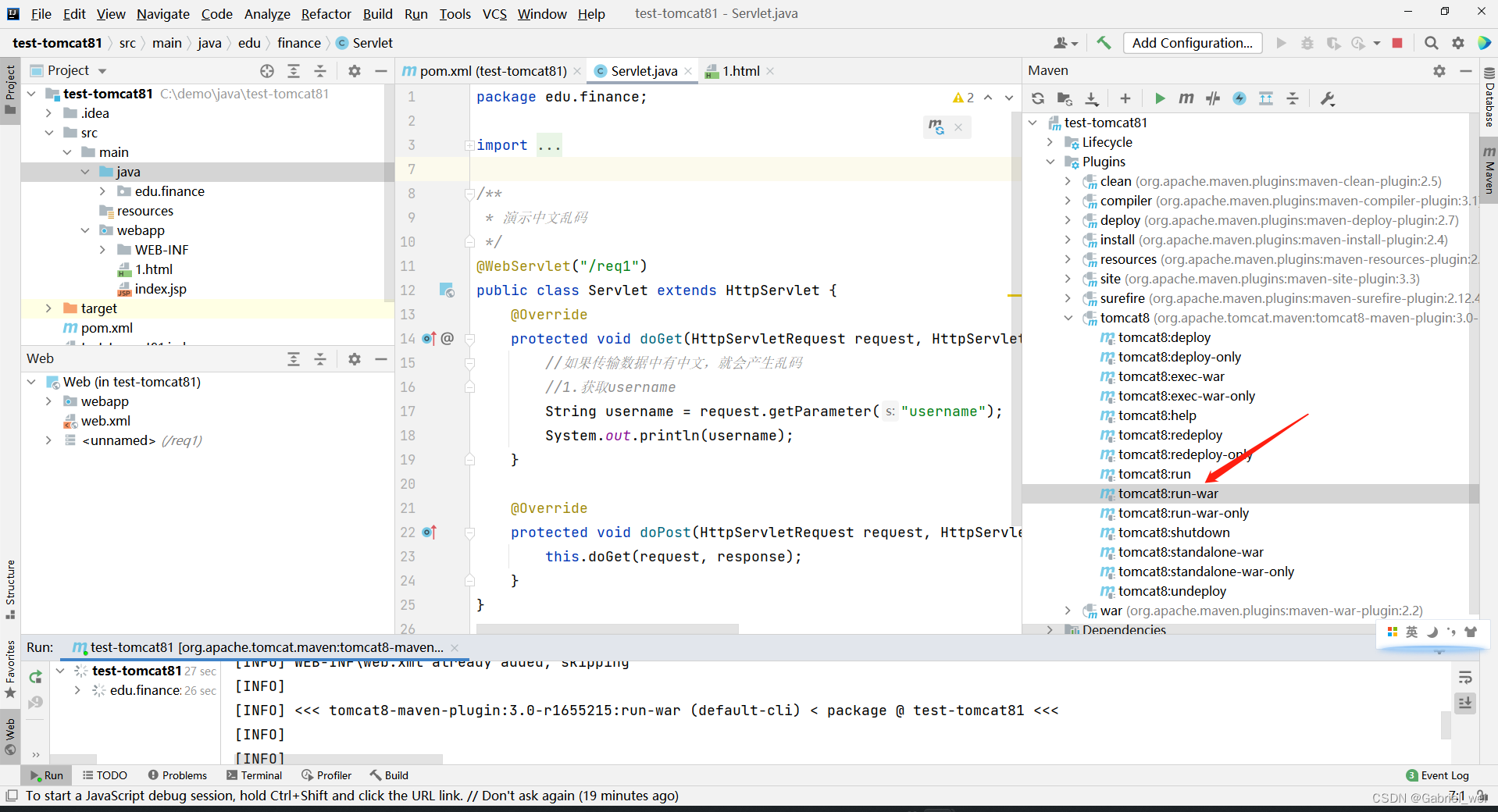
IDEA中使用tomcat8-maven-plugin插件
第一种方式 pom.xml <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.or…...
2023年妇女节是哪一天 妇女节是2023年几月几日?
2023年妇女节是哪一天是2023年几月几日? 2023年妇女节是2023年3月8日 三八妇女节是国家法定节假日吗? 妇女节不是国家法定节假日,而国家法定节假日包括:元旦、春节、清明节、劳动节、端午节、中秋节、国庆节; 关于三…...
如何运维多集群数据库?58 同城 NebulaGraph Database 运维实践
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SktQW2qn-1676450580889)(https://www-cdn.nebula-graph.com.cn/nebula-website-5.0/images/blogs/58.%20Com%20Inc/58%E5%90%8C%E5%9F%8E_%E7%94%BB%E6%9D%BF%201.jpg)] 图计算业务背景介绍 我们为什…...
尚医通(十四)Spring Cloud GateWay网关 | 跨域 | 权限认证
目录一、网关基本概念1、API网关介绍2、Spring Cloud Gateway3、Spring Cloud Gateway核心概念二、创建service_gateway模块(网关服务)1、创建service_gateway模块2、在pom.xml引入依赖3、编写application.properties配置文件4、编写启动类5、前端端口号…...

PO模式在Selenium中简单实践
初识PO模式 PO(PageObject)是一种设计模式。简单来说就是把一些繁琐的定位方法、元素操作方式等封装到类中,通过类与类之间的调用完成特定操作。 PO被认为是自动化测试项目开发实践的最佳设计模式之一。 在学习PO模式前,可以先…...
KubeSphere
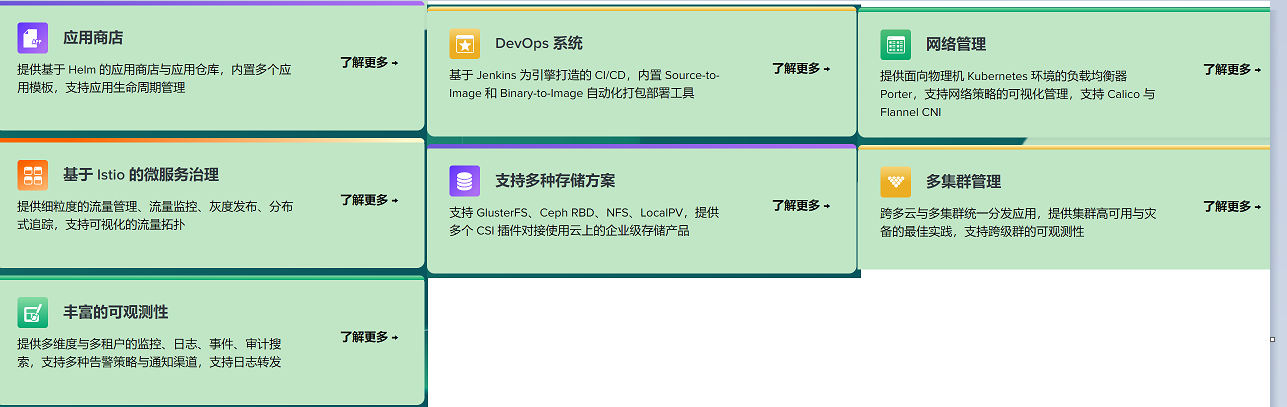
文章目录一、概述二、最小化安装 KubeSphere2.1 前提2.2 安装 nfs 服务器一、概述 KubeSphere是在Kubernetes之上构建的以应用为中心的企业级分布式容器平台,提供简单易用的操作界面以及向导式操作方式,在降低用户使用容器调度平台学习成本的同时&#…...
必备)
JAVA基础阶段面试题(关键点)必备
1、简述什么是 JDK、JRE 和 JVM? JDK : 开发工具包JRE : 运行时环境JVM : java虚拟机2、写出Java的四类八种基本数据类?整数 byte short int long小数(浮点) float double布尔 boolean字符 char3、& 和 && 的区别 ?& 符号的左右两边,无…...
Shiro简介
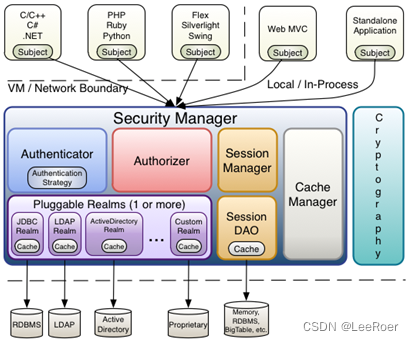
介绍 ApacheShiro 是一个功能强大且易于使用的 Java 安全(权限)框架。Shiro 可以完成:认证、授权、加密、会话管理、与 Web集成、缓存等。借助Shiro 您可以快速轻松地保护任何应用程序一一从最小的移动应用程序到最大的 Web 和企业应用程序。 1.2:为什么要用 shiro 自2003年以…...

cmu 445 poject 3笔记
2022年的任务 https://15445.courses.cs.cmu.edu/fall2022/project3/ task1, 从磁盘读取数据的算子 task2, 聚合和join算子 task3, sort,limit,topn算子,以及sortlimit->TopN优化 leaderboard没做 本文不写代码,只记录遇到的一些思维盲点 Task1 scan…...

CHAPTER 2 Zabbix界面操作
Zabbix界面操作2.1 Zabbix界面操作1.zabbix的web界面安装2.添加监控信息3.查看监控内容4.查看图像2.2 自定义监控与监控报警1.自定义监控1.1 说明1.2 预备知识2.实现自定义监控2.1 自定义语法2.2 agent注册2.3 在server端注册(web操作)2.4 查看监控图形2.3 监控报警1.第三方报警…...

keep-alive的使用-及遇到的问题
被keep-alive包括的的组件,当组件切换是不是走销毁流程,而是缓存起来 keep-alive有三个参数include匹配name名被缓存,exclude匹配name名不会被缓存,max被缓存组件数量 不写,组件默认全部缓存 <keep-alive ><…...
华为OD面试经验分享,尤其注意机试题部分
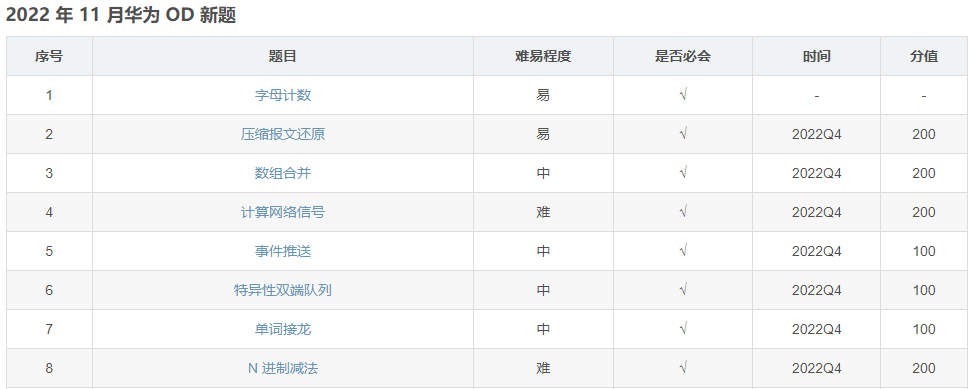
文章目录招聘流程和背景介绍面试准备机试题目类型和解答技巧在算法部分在操作系统部分面试官提问和答题技巧面试总结和建议推荐一些华为 od 常见的机试题题目:两数之和题目:二叉树的遍历题目:链表反转题目:最大子序和招聘流程和背…...

【Java】String、StringBuffer、StringBuilder的区别
一、String 由 char[] 数组构成,使用了 final 修饰,String的值是不可变的,这就导致每次对String的操作都会生成新的String对象,然后把指针指向新的引用对象,不仅效率低下,而且浪费大量优先的内存空间。 二…...

iOS开发:对Block使用的一次研究总结
在开发中Block是经常使用的,那我们就得知其然,知其所以然。 Block是什么? Block可以封装一个匿名函数为对象,并捕获上下文所需的数据,并传给目标对象在适当的时候回调。我们使用Block的目的其实就是回调传值,那我们去看看Block的底层,再深入了解一下Block。 Block的底…...

Spark 3.1.1 shuffle fetch 导致shuffle错位的问题
背景 最近从数据仓库小组那边反馈了一个问题,一个SQL任务出来的结果不正确,重新运行一次之后就没问题了,具体的SQL如下: select col1,count(1) as cnt from table1 where dt 20230202 group by col1 having count(1) > 1这个问题是偶发…...
2月第2周榜单丨飞瓜数据B站UP主排行榜(哔哩哔哩平台)发布!
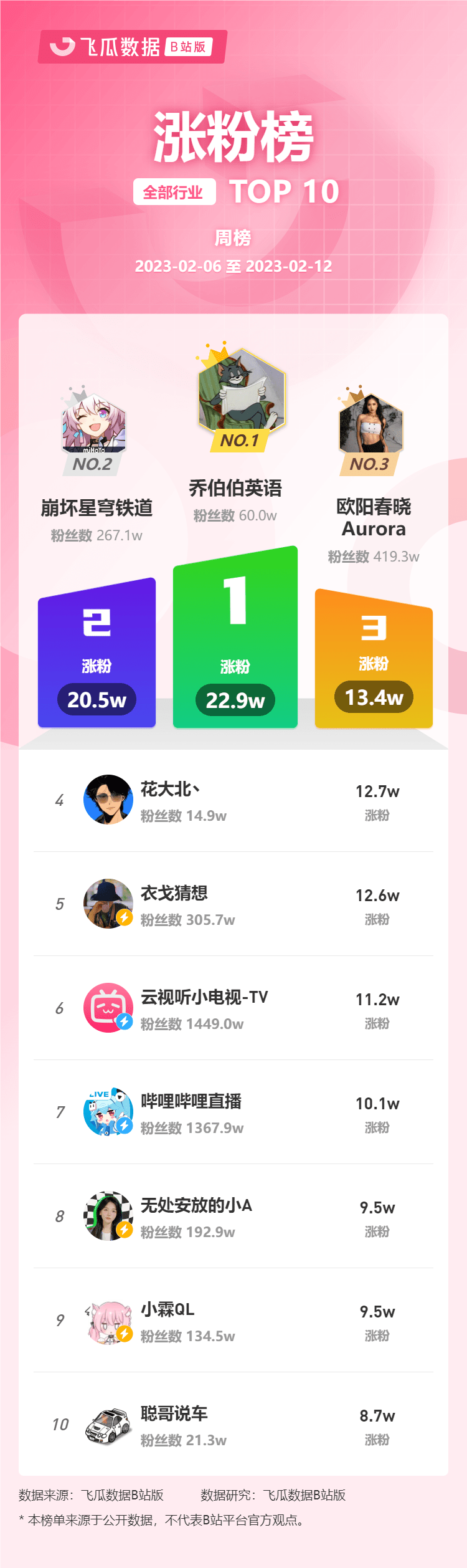
飞瓜轻数发布2023年2月6日-2月12日飞瓜数据UP主排行榜(B站平台),通过充电数、涨粉数、成长指数三个维度来体现UP主账号成长的情况,为用户提供B站号综合价值的数据参考,根据UP主成长情况用户能够快速找到运营能力强的B站…...
Jdk19 动态编译 Java源码为 Class 文件
动态编译 Java 源码为 Class一.背景1.Jdk 版本2.需求二.Java 源码动态编译实现1.Maven 依赖2.源码包装类3.Java 文件对象封装类4.文件管理器封装类5.类加载器6.类编译器三.动态编译测试1.普通测试类2.接口实现类3.测试四.用动态编译 Class 替换 SpringBoot 的 Bean(…...
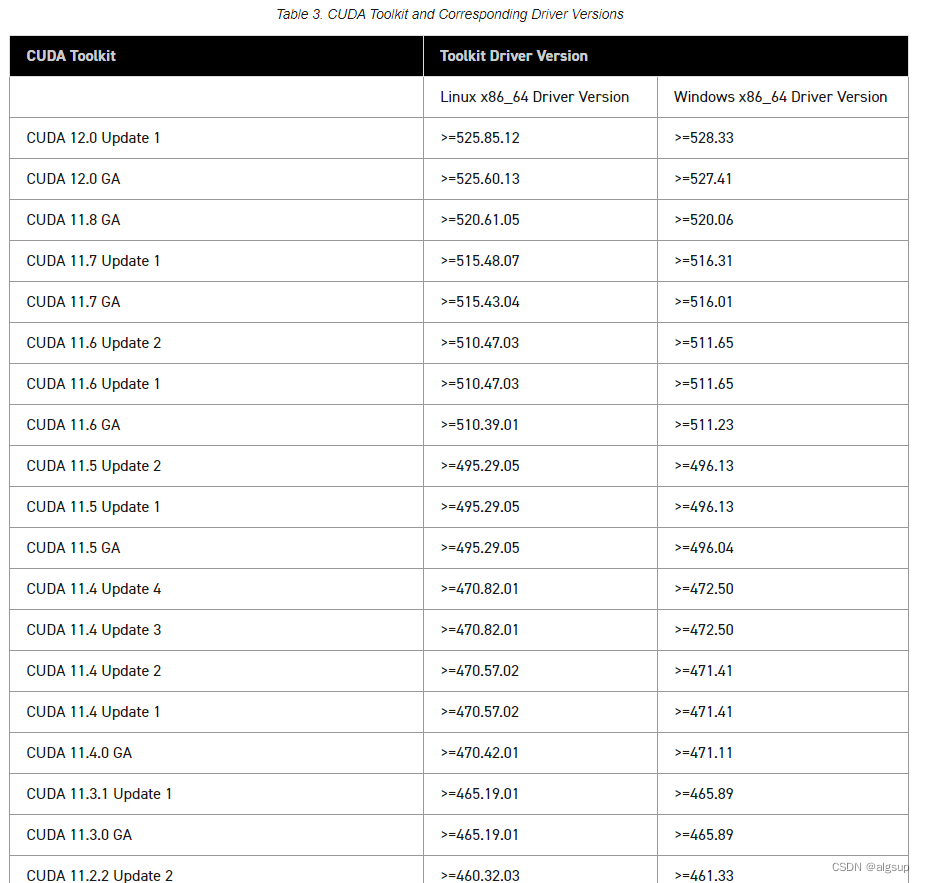
安装 GPU 版本的 tensorflow 完整版本
前言: 之前安装的 CPU 版本的 tensorflow 一直出问题,索性就直接安装 GPU 版本的 tensorflow 了(有了GPU 就不能浪费)。 安装过程: 1)看自己有无 GPU,找到对应 GPU 的版本:任务管理…...

BOM编程-设置地址栏上的URL
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>设置地址栏上的URL</title> </head> <body> <script> function go(){ // 获…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
