凸包及其算法
概念
凸包:一个能够将所有给定点围住的最小周长封闭图形。
稳定凸包:在当前组成凸包的点集 V0V_0V0 中新增一个不在凸包上的点,形成新点集 V1V_1V1,若可以使 V1V_1V1 中所有点都在 V1V_1V1 的点的凸包上,则这个凸包不稳定。反之,则是稳定凸包。
求解凸包
问题
给定在平面直角坐标系中 nnn 个点 Pi(xi,yi)P_i(x_i,y_i)Pi(xi,yi),求解这些点的凸包。
思考
因为凸包是最小周长的封闭图形,所以凸包一定是由多条线段构成的,毕竟两点之间直线最短。
也就是说,凸包一定是多边形。说了跟说了一样
暴力算法
可以发现,对于凸包的一条边,这条边所在的直线一定使得所有点都在其左边或者右边。
所以枚举两个点 P0,P1P_0, P_1P0,P1,判断所有点是否在 P0P1P_0P_1P0P1 同一边。
时间复杂度 O(n2)O(n^2)O(n2)
分治
横坐标最大和最小的两点一定在凸包上。而且这两点将凸包分为上凸和下凸。
然后分别对上凸包和下凸包用分治进行求解。
若是上凸包,假设当前分治到点 Pl,PrP_l, P_rPl,Pr 之间,则 PmidP_{mid}Pmid 为在 PlPrP_lP_rPlPr 上方离 PlPrP_lP_rPlPr 最远的节点,然后继续分治 PlPmid,PmidPrP_lP_{mid}, P_{mid}P_rPlPmid,PmidPr。
若是下凸包,则 PmidP_{mid}Pmid 为在 PlPrP_lP_rPlPr 下方离 PlPrP_lP_rPlPr 最远的节点。其他同理。
时间复杂度 O(nlogn)O(n\log n)O(nlogn)
Graham扫描法
设 P0P_0P0 为 yyy 坐标最小的点。(然后将 yyy 坐标最小的点从 PPP 中删除)
将除 P0P_0P0 外点按照以 P0P_0P0 为极点、任意一条从 P0P_0P0 出发的射线为极轴的极坐标排序。(此处按逆时针方向排序)
然后将 P0P_0P0 丢入当前凸包。
接下来假设 PPP 已经按照极坐标排序,DDD 表示凸包内的点(DDD 内点按照加入顺序排序,即 D0D_0D0 是第一个加入的)。
将排好序的点依次访问,更新凸包,假设当前点为 PiP_iPi,当前凸包内点为 D0,D1,...,DdD_0,D_1,...,D_dD0,D1,...,Dd。
由于是逆时针排序的,所以 DDD 中点按顺序组成的每条边相对与上一条边一定往左偏。
我们判断 PiDdP_iD_dPiDd 与 DdDd−1D_dD_{d -1}DdDd−1 的关系。若 PiDdP_iD_dPiDd 相当于 DdDd−1D_dD_{d -1}DdDd−1 往右偏,则 DdD_dDd 在 PiDd−1P_iD_{d-1}PiDd−1 左侧,我们将 DdD_dDd 删除,然后 ddd 减一。
若PiDdP_iD_dPiDd 相当于 DdDd−1D_dD_{d -1}DdDd−1 往左偏,则不需要删除。继续 Pi+1P_{i+1}Pi+1。
相关文章:

凸包及其算法
概念 凸包:一个能够将所有给定点围住的最小周长封闭图形。 稳定凸包:在当前组成凸包的点集 V0V_0V0 中新增一个不在凸包上的点,形成新点集 V1V_1V1,若可以使 V1V_1V1 中所有点都在 V1V_1V1 的点的凸包上,则这…...

计算机网络学习笔记(二)物理层
物理层(传输比特0/1)基本概念 物理层下的传输媒体 1. 导引型 同轴电缆,双绞线(绞合可抵御干扰),光纤,电力线 2. 非导引型(调制振幅 频率 相位) 无线电波,微…...

为什么职称要提前准备?
职称反映专业技术人员的学术和技术水平、工作能力的工作成就,具有学衔、岗位两种性质。目前中国现状下,职称主要代表社会地位,就业经验,职称等级越高,越容易得到更高的社会经济和福利待遇。 职称通过申报、评审的形式…...

MyBatis详解1——相关配置
一、什么是MyBatis 1.定义:是一个优秀的持久层框架(ORM框架),它支持自定义 SQL、存储过程以及高级映射。MyBatis是一个用来更加简单的操作和读取数据库的工具。 2.支持的操作方式:xml或者注解实现操作(xm…...
字节青训营——秒杀系统设计学习笔记(三)
限流算法 限流顾名思义,就是对请求或并发数进行限制;通过对一个时间窗口内的请求量进行限制来保障系统的正常运行。如果我们的服务资源有限、处理能力有限,就需要对调用我们服务的上游请求进行限制,以防止自身服务由于资源耗尽而…...

每天一道大厂SQL题【Day10】电商分组TopK实战
每天一道大厂SQL题【Day10】电商分组TopK实战 大家好,我是Maynor。相信大家和我一样,都有一个大厂梦,作为一名资深大数据选手,深知SQL重要性,接下来我准备用100天时间,基于大数据岗面试中的经典SQL题&…...
最全的免费录屏工具,这 19 款录屏软件绝对值得你收藏
屏幕录制软件可让您捕获屏幕以与他人共享,创建与产品相关的视频、教程、课程、演示、视频等。这些软件是您能够从网络摄像头和屏幕录制视频。以下是精选的顶级屏幕录像机列表。 适用于 PC 的19 款免费录屏屏幕录像机软件 1)奇客免费录屏 奇客免费录屏&am…...
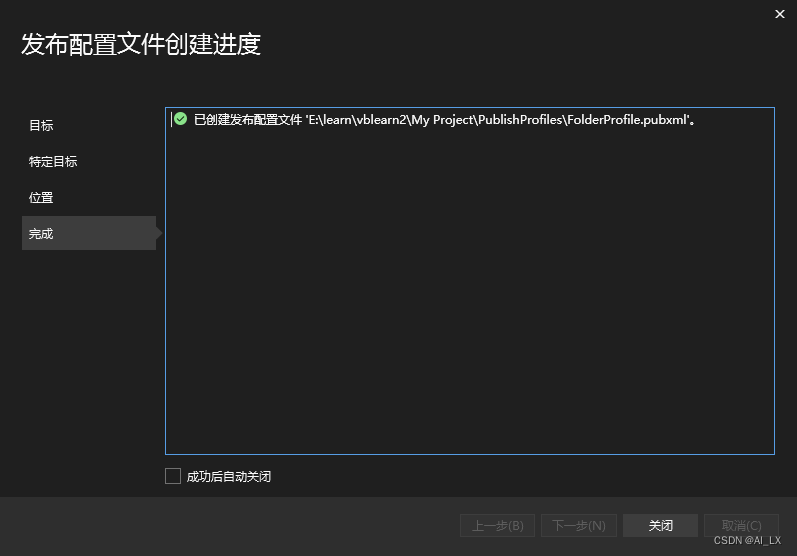
vb.net计算之.net core基础(2)-发布应用
目录 发布程序测试运行运行方式发布程序 首先,将编译配置改为Release 然后,发布应用,在生成菜单下。 选择发布到文件夹 继续选择文件夹 接着,完成 关闭 点击发布标签栏的发布按钮...
微服务项目【商品秒杀接口压测及优化】
生成测试用户 将UserUtils工具类导入到zmall-user模块中,运行生成测试用户信息,可根据自身电脑情况来生成用户数量。 UserUtils: package com.xujie.zmall.utils;import com.alibaba.nacos.common.utils.MD5Utils; import com.fasterxml.j…...

1997. 访问完所有房间的第一天
题目 你需要访问 n 个房间,房间从 0 到 n - 1 编号。同时,每一天都有一个日期编号,从 0 开始,依天数递增。你每天都会访问一个房间。 最开始的第 0 天,你访问 0 号房间。给你一个长度为 n 且 下标从 0 开始 的数组 n…...

通达信交易接口以什么形式执行下单的?
通达信程交易接口 以API形式来执行下单接口,一般不再需要通过接口系统之间进行连接,通过直接调用通达信dll交易函数的方式直接进行交易,包括下单,撤单,查询资金股份、当日委托、当日成交等方面都能很快的执行出来。以a…...

CobaltStrike上线微信通知
CobaltStrike上线微信通知 利用pushplus公众号(每天免费发送200条消息) http://www.pushplus.plus/push1.html 扫码登录后需要复制token 可以测试一下发送一下消息,手机会受到如下消息。可以在微信提示里将消息免打扰关闭(默认…...

喜茶、奈雪的茶“花式”寻生路
配图来自Canva可画 疫情全面开放不少人“阳了又阳”,电解质饮品成为热销品,梨子、橘子、柠檬等水果被卖断货,凉茶、黄桃罐头被抢购一空,喜茶的“多肉大橘”、奈雪的“霸气银耳炖梨”、蜜雪冰城的“棒打鲜橙”、沪上阿姨的“鲜炖整…...

Xstream使用教程
1.Xstream介绍 官网:https://x-stream.github.io/tutorial.html 介绍:XStream 对象序列化和反序列化为 XML的一个JAVA类库。JDK 1.4以上适用。 PS:与JAXB相比,Xstream更好用一些,像XStreamImplicit这种注解,我在JAX…...
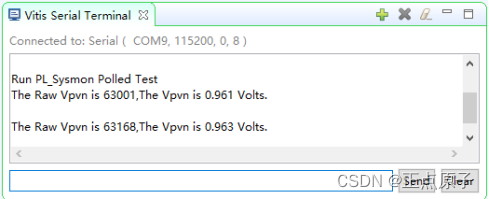
【正点原子FPGA连载】第十一章PL SYSMON测量输入模拟电压 摘自【正点原子】DFZU2EG_4EV MPSoC之嵌入式Vitis开发指南
1)实验平台:正点原子MPSoC开发板 2)平台购买地址:https://detail.tmall.com/item.htm?id692450874670 3)全套实验源码手册视频下载地址: http://www.openedv.com/thread-340252-1-1.html 第十一章PL SYSM…...

纷享销客百思特 | 数字化营销赋能企业新增长沙龙圆满落幕
为进一步帮助企业客户实现数字化转型,纷享销客联合百思特管理咨询集团,于2月10日举办 “数字化营销赋能企业新增长”主题沙龙。本次活动以“新变革新增长”为主题,现场30余位制造企业高管齐聚一堂,共同探讨企业如何在当前复杂的宏…...

oracle查看具体表占用空间 oracle查看表属于哪个用户
文章目录前言oracle查看具体表占用空间1、查看表空间总大小、使用率、剩余空间2、查看具体表的占用空间大小3、查看表空间对应日志文件oracle查看表属于哪个用户1、oracle怎么查看表属于哪个用户2、Oracle查询视图所属用户3、Oracle查询存储过程所属用户总结前言 表空间是数据…...
2.Visual Studio下载和安装
Visual Studio 是微软提供的一个集成开发环境(IDE),主要用于为 Windows 系统开发应用程序。Visual Studio 提供了构建 .Net 平台应用程序的一站式服务,可以使用 Visual Studio 开发、调试和运行应用程序。 1、Visual Studio下载 …...
)
「4」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 第四章 向量组的线性相关性 &2)向量组的线性相关性 &3)向…...
IDEA中使用tomcat8-maven-plugin插件
第一种方式 pom.xml <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.or…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
