LA@特征值和特征向量
文章目录
- 特征值和特征向量
- 例
- 例
- 求解方阵的特征值和特征向量🎈
- 特征多项式@特征方程
- 方阵特征值和特征向量的性质
- 证明
- 推论
- 衍生特征值
- 更一般的
- 转置和特征值
- 其他结论(方阵多项式的特征值与方阵本身特征值的关系)
- 特征向量线性相关性
特征值和特征向量
-
许多定量分析模型中,常常需要寻求数λ\lambdaλ和非零向量α\alphaα,使得Aα=λαA\alpha=\lambda\alphaAα=λα
-
一般特征值和特征向量是成对存在的,在概念上,是不可分割且相互依赖地同时定义出来
-
设A是n阶方阵
-
如果存在数λ\lambdaλ和n维非零列向量α(α≠0)\alpha(\alpha\neq{0})α(α=0),满足
-
Aα=λα或(λα−Aα=0;(λE−A)α=0)A\alpha=\lambda\alpha \\或(\lambda\alpha-A\alpha=0;(\lambda{E}-A)\alpha=0) Aα=λα或(λα−Aα=0;(λE−A)α=0)
-
称λ\lambdaλ是方阵A的一个特征值
-
α\alphaα为方阵A的对应于λ\lambdaλ的一个特征向量
-
-
-
特征值问题是对方阵而言的,如果说矩阵的特征值或特征向量,那么这个矩阵默认是方阵
例
(3122)(11)=(44)=4(11)\begin{pmatrix} 3&1 \\ 2&2 \end{pmatrix} \begin{pmatrix} 1\\ 1 \end{pmatrix} =\begin{pmatrix} 4 \\ 4 \end{pmatrix} =4\begin{pmatrix} 1 \\ 1 \end{pmatrix} (3212)(11)=(44)=4(11)
-
上述等式链告诉我们,矩阵
-
A=(3122)作用在向量α=(11)上的效果和常数4作用在α上的效果在乘法上是一样的A=\begin{pmatrix} 3&1 \\ 2&2 \end{pmatrix} 作用在向量\alpha=\begin{pmatrix} 1\\ 1 \end{pmatrix} \\上的效果和常数4作用在\alpha上的效果在乘法上是一样的 A=(3212)作用在向量α=(11)上的效果和常数4作用在α上的效果在乘法上是一样的
- 也就是说,矩阵左乘特征向量的结果和特征向量左乘特征向量的结果一样
-
例
-
设A2=AA^2=AA2=A,证明A的特征值为0或1
-
Aα=λαA2α=A(Aα)=Aλα=λ(Aα)=λ(λα)=λ2α又A2=A;A2α=Aα=λαA\alpha=\lambda{\alpha} \\A^2\alpha=A(A\alpha)=A\lambda\alpha=\lambda{(A\alpha)}=\lambda(\lambda\alpha)=\lambda^2\alpha \\又A^2=A;A^2\alpha=A\alpha=\lambda\alpha Aα=λαA2α=A(Aα)=Aλα=λ(Aα)=λ(λα)=λ2α又A2=A;A2α=Aα=λα
-
∴λ2α=λα(λ2−λ)α=0,α≠0λ2−λ=λ(λ−1)=0λ=0或1\\\therefore \lambda^2\alpha=\lambda\alpha \\(\lambda^2-\lambda)\alpha=\bold{0},\alpha\neq\bold0 \\\lambda^2-\lambda=\lambda(\lambda-1)=0 \\\lambda=0或1 ∴λ2α=λα(λ2−λ)α=0,α=0λ2−λ=λ(λ−1)=0λ=0或1
-
-
方法2:
-
同时对Aα=λα左乘A:A2α=λ(Aα)Aα=λ2αλα=λ2α同时对A\alpha=\lambda\alpha左乘A: \\A^2\alpha=\lambda(A\alpha) \\A\alpha=\lambda^{2}\alpha \\\lambda\alpha=\lambda^2{\alpha} 同时对Aα=λα左乘A:A2α=λ(Aα)Aα=λ2αλα=λ2α
-
其余和方法1一致
-
求解方阵的特征值和特征向量🎈
-
对于方程组S
(λE−A)α=0;α≠0(\lambda{E}-A)\alpha=\bold0;\alpha\neq{\bold0} (λE−A)α=0;α=0- 由于α≠0由于\alpha\neq{\bold0}由于α=0,所以α\alphaα是齐次线性方程组(λE−A)x=0(\lambda{E}-A)x=\bold0(λE−A)x=0的非零解
- 而上述齐次线性方程组有非零解,仅当其系数行列式为0
- 即矩阵A的特征值λ\lambdaλ是方程∣λE−A∣=0|\lambda{E}-A|=0∣λE−A∣=0的根
- 如果A是一个n阶方阵,则A在复数范围内恰有n个特征值(包括重根)
- 即使矩阵A的元素全为实数,其特征值也可能是复数
特征多项式@特征方程
-
设n阶方阵A=(aij)A=(a_{ij})A=(aij)
-
f(λ)=∣λE−A∣=∣λ−a11−a12⋯−a1n−a21λ−a22⋯−a2n⋮⋮⋮−an1−an2⋯λ−ann∣f(\lambda)=|\lambda{E}-A|= \begin{vmatrix} \lambda-a_{11}& -a_{12}& \cdots&-a_{1n} \\ -a_{21}& \lambda-a_{22}& \cdots&-a_{2n} \\ \vdots& \vdots& &\vdots \\ -a_{n1}& -a_{n2}& \cdots&\lambda-a_{nn} \\ \end{vmatrix} f(λ)=∣λE−A∣=λ−a11−a21⋮−an1−a12λ−a22⋮−an2⋯⋯⋯−a1n−a2n⋮λ−ann
-
−A=(−a11−a12⋯−a1n−a21−a22⋯−a2n⋮⋮⋮−an1−an2⋯−ann)λE=(λ0⋯00λ⋯0⋮⋮⋮00⋯λ)-A=\begin{pmatrix} -a_{11}& -a_{12}& \cdots&-a_{1n} \\ -a_{21}& -a_{22}& \cdots&-a_{2n} \\ \vdots& \vdots& &\vdots \\ -a_{n1}& -a_{n2}& \cdots&-a_{nn} \\ \end{pmatrix} \\ \lambda{E}= \begin{pmatrix} \lambda& 0& \cdots&0 \\ 0& \lambda& \cdots&0 \\ \vdots& \vdots& &\vdots \\ 0& 0& \cdots&\lambda \\ \end{pmatrix} −A=−a11−a21⋮−an1−a12−a22⋮−an2⋯⋯⋯−a1n−a2n⋮−annλE=λ0⋮00λ⋮0⋯⋯⋯00⋮λ
-
f(λ)f(\lambda)f(λ)是A的特征多项式
-
f(λ)=0f(\lambda)=0f(λ)=0(即∣λE−A∣=0|\lambda{E}-A|=\bold{0}∣λE−A∣=0)是A的特征方程
-
-
求解特征方程f(λ)=0f(\lambda)=0f(λ)=0的全部根,他们就是n阶方阵A的特征值,将他们记为λi,i=1,2,⋯,n\lambda_i,i=1,2,\cdots,nλi,i=1,2,⋯,n
-
对于每个λi\lambda_iλi,求解对应的齐次线性方程组(λiE−A)x=0(\lambda_i{E-A})x=\bold0(λiE−A)x=0
- 不妨将方阵Bi=λiE−AB_i=\lambda_{i}E-ABi=λiE−A,便于讨论
- 求齐次线性方程Bix=0B_ix=0Bix=0一组基础解系:Φ=α1,α2,⋯,αsi\Phi=\alpha_1,\alpha_2,\cdots,\alpha_{s_i}Φ=α1,α2,⋯,αsi,si=n−ris_i=n-r_isi=n−ri
- 则方阵A关于λi\lambda_iλi的全部特征向量表示为∑j=1sikjαj\sum\limits_{j=1}^{s_i}k_j\alpha_jj=1∑sikjαj
-
方阵特征值和特征向量的性质
-
代数学基本定理:任何一个非零的一元n次复系数多项式,都正好有n个复数根(重根视为多个根)
-
∑i=1nλi=∑i=1naii,\sum\limits_{i=1}^{n}\lambda_i=\sum\limits_{i=1}^{n}a_{ii}, i=1∑nλi=i=1∑naii,
- 其中∑i=1naii称为矩阵的迹其中\sum_{i=1}^{n}a_{ii}称为矩阵的迹其中∑i=1naii称为矩阵的迹
-
∏i=1nλi=∣A∣\prod_{i=1}^{n}\lambda_{i}=|A| i=1∏nλi=∣A∣
证明
-
对于n次多项式f(λ)f(\lambda)f(λ),他有n个复根,可以因式分解写成如下形式
- f(λ)=(λ−λ1)(λ−λ2)⋯(λ−λn)f(\lambda)=(\lambda-\lambda_1)(\lambda-\lambda_2)\cdots(\lambda-\lambda_n)f(λ)=(λ−λ1)(λ−λ2)⋯(λ−λn)
-
对于
-
f(λ)=∣λE−A∣=∣λ−a11−a12⋯−a1n−a21λ−a22⋯−a2n⋮⋮⋮−an1−an2⋯λ−ann∣不妨把这个行列式记为B,B=f(λ)f(\lambda)=|\lambda{E}-A|= \begin{vmatrix} \lambda-a_{11}& -a_{12}& \cdots&-a_{1n} \\ -a_{21}& \lambda-a_{22}& \cdots&-a_{2n} \\ \vdots& \vdots& &\vdots \\ -a_{n1}& -a_{n2}& \cdots&\lambda-a_{nn} \\ \end{vmatrix} \\不妨把这个行列式记为B,B=f(\lambda) f(λ)=∣λE−A∣=λ−a11−a21⋮−an1−a12λ−a22⋮−an2⋯⋯⋯−a1n−a2n⋮λ−ann不妨把这个行列式记为B,B=f(λ)
-
f(λ)f(\lambda)f(λ)行列式展开后有n!项(未合化简同类项前),把它们记为θk,k=1,2,⋯,n!\theta_k,k=1,2,\cdots,n!θk,k=1,2,⋯,n!
- 是一个n次多项式
- 因为其中有1项是由主对角线元素相乘的积),把它记为
- ξ=θp=(λ−a11)(λ−a22)⋯(λ−ann)\xi=\theta_p=(\lambda-a_{11})(\lambda-a_{22})\cdots(\lambda-a_{nn})ξ=θp=(λ−a11)(λ−a22)⋯(λ−ann)
- 其余项之多含有对角线元素的n-2个元素(因为每个项的因子都取自不同行不同列)
- 如果θk\theta_kθk中有一个元素eije_{ij}eij不在主对角线上(i≠ji\neq{j}i=j)那么以为着θk\theta_{k}θk中不可能含有bii和bjjb_{ii}和b_{jj}bii和bjj
- 因为其中有1项是由主对角线元素相乘的积),把它记为
- 是一个n次多项式
-
现在,我们只对ξ\xiξ这一项感兴趣
- θp=λn−(a11+a22+⋯+ann)λn−1+⋯\theta_p=\lambda^{n}-(a_{11}+a_{22}+\cdots+a_{nn})\lambda^{n-1}+\cdotsθp=λn−(a11+a22+⋯+ann)λn−1+⋯
- f(λ)=θp+∑i,i≠pn!θif(\lambda)=\theta_p+\sum\limits_{i,i\neq{p}}^{n!}\theta_if(λ)=θp+i,i=p∑n!θi
- (注意,展开式中n,n−1n,n-1n,n−1次项的系数是只由θp\theta_pθp提供,其余θi,i≠p\theta_i,i\neq{p}θi,i=p只能够提供不超过n−2n-2n−2次项;
- 常数项可以通过取λ=0\lambda=0λ=0得到,即f(0)=∣0E−A∣=∣−A∣=(−1)n∣A∣f(0)=|0E-A|=|-A|=(-1)^n|A|f(0)=∣0E−A∣=∣−A∣=(−1)n∣A∣
- f(λ)=λn−(a11+a22+⋯+ann)λn−1+⋯∣−A∣λ0f(\lambda)=\lambda^{n}-(a_{11}+a_{22}+\cdots+a_{nn})\lambda^{n-1}+\cdots|-A|\lambda^{0}f(λ)=λn−(a11+a22+⋯+ann)λn−1+⋯∣−A∣λ0
- 为什么是这样的,可以参考:math@多项式@求和式乘法@代数学基本定理_xuchaoxin1375的博客-CSDN博客
-
另一方面,设λ1,⋯,λn\lambda_1,\cdots,\lambda_nλ1,⋯,λn是f(λ)f(\lambda)f(λ)的n个特征值(根)
-
f(λ)=∏i(λ−λi)=λn−(∑i=1nλi)λn−1+⋯+∏i=1n(−λi)f(\lambda)=\prod_{i}(\lambda-\lambda_i) =\lambda^n-(\sum_{i=1}^{n}\lambda_i)\lambda^{n-1}+\cdots+\prod_{i=1}^{n}(-\lambda_i) f(λ)=i∏(λ−λi)=λn−(i=1∑nλi)λn−1+⋯+i=1∏n(−λi)
-
对比n−1n-1n−1次项的系数∑i=1naii=∑i=1nλi\sum_{i=1}^{n}a_{ii}=\sum_{i=1}^{n}\lambda_{i}∑i=1naii=∑i=1nλi
-
对比000此项系数∣−A∣=∏i=1n(−λi)|-A|=\prod_{i=1}^{n}(-\lambda_i)∣−A∣=∏i=1n(−λi),即(−1)n∣A∣=(−1)n∏in(λi)(-1)^n|A|=(-1)^n\prod_{i}^{n}(\lambda_i)(−1)n∣A∣=(−1)n∏in(λi),∣A∣=∏inλi|A|=\prod_{i}^{n}\lambda_i∣A∣=∏inλi
-
-
-
推论
- 方阵A可逆的条件是A的特征值不全为0
衍生特征值
- 设α\alphaα是矩阵A属于特征值λ0\lambda_0λ0的特征向量(记为α,A→λ\alpha,{A}\to{\lambda}α,A→λ,或者更直接的Aα=λ0αA\alpha=\lambda_0\alphaAα=λ0α)
- 设α,γ,A,λ0\alpha,\gamma,A,\lambda_0α,γ,A,λ0满足Aα=λ0α;Aγ=λ0γA\alpha=\lambda_{0}\alpha;A\gamma=\lambda_0\gammaAα=λ0α;Aγ=λ0γ,则:
- β=kα\beta=k\alphaβ=kα满足Aβ=λ0βA\beta=\lambda_0\betaAβ=λ0β
- 因为A(kα)=kAα=kλ0α=λ0(kα)A(k\alpha)=kA\alpha=k\lambda_0{\alpha}=\lambda_{0}(k\alpha)A(kα)=kAα=kλ0α=λ0(kα)
- ϕ=α+γ\phi=\alpha+\gammaϕ=α+γ满足Aϕ=λ0ϕA\phi=\lambda_0\phiAϕ=λ0ϕ
- A(α+γ)=Aα+Aγ=λ0α+λ0γ=λ0(α+γ)A(\alpha+\gamma)=A\alpha+A\gamma=\lambda_0\alpha+\lambda_0\gamma=\lambda_0(\alpha+\gamma)A(α+γ)=Aα+Aγ=λ0α+λ0γ=λ0(α+γ)
- 综合上述结论,可以得出:若αi,i=1,2,⋯,n\alpha_i,i=1,2,\cdots,nαi,i=1,2,⋯,n,λ,A,λ0\lambda,A,\lambda_0λ,A,λ0满足Aαi=αiλ0A\alpha_i=\alpha_i\lambda_0Aαi=αiλ0,则αi\alpha_iαi的任意线性组合θ=∑ikiαi\theta=\sum_i{k_i\alpha_i}θ=∑ikiαi满足Aθ=θλ0A\theta=\theta\lambda_0Aθ=θλ0
- β=kα\beta=k\alphaβ=kα满足Aβ=λ0βA\beta=\lambda_0\betaAβ=λ0β
更一般的
-
设α,A,λ\alpha,A,\lambdaα,A,λ满足Aα=λαA\alpha=\lambda{\alpha}Aα=λα,则:
-
对Aα=λαA\alpha=\lambda{\alpha}Aα=λα同乘以kkk,
- (kA)α=(kλ)α(kA)\alpha=(k\lambda)\alpha(kA)α=(kλ)α,
- A(kα)=λ(kα)A(k\alpha)=\lambda({k\alpha})A(kα)=λ(kα)
-
再次乘以kkk
- (kA)(kα)=(kλ)(kα)(kA)(k\alpha)=(k\lambda){(k\alpha)}(kA)(kα)=(kλ)(kα)
-
对Aα=λαA\alpha=\lambda\alphaAα=λα两边同时左乘AAA
- AAα=Aλα=λAα=λλαAA\alpha=A\lambda\alpha=\lambda{A\alpha}=\lambda{\lambda{\alpha}}AAα=Aλα=λAα=λλα
- A2α=λ2αA^2\alpha=\lambda^2\alphaA2α=λ2α
- A3α=Aλ2α,λ2Aα=λ3αA^3\alpha=A\lambda^2\alpha,\lambda^2A\alpha=\lambda^3\alphaA3α=Aλ2α,λ2Aα=λ3α
- 重复m-1次得到:Amα=λmαA^m\alpha=\lambda^m\alphaAmα=λmα
-
当AAA可逆时
- λ−1α=A−1α\lambda^{-1}\alpha=A^{-1}\alphaλ−1α=A−1α
- 对Aα=λαA\alpha=\lambda{\alpha}Aα=λα同时左乘A−1A^{-1}A−1
- α=λA−1α\alpha=\lambda A^{-1}\alphaα=λA−1α,两边同乘以λ−1\lambda^{-1}λ−1,λ−1α=A−1α\lambda^{-1}\alpha=A^{-1}\alphaλ−1α=A−1α
- (A∗)α=∣A∣λα(A^*)\alpha=\frac{|A|}{\lambda}\alpha(A∗)α=λ∣A∣α
- A−1=1∣A∣A∗A^{-1}=\frac{1}{|A|}A^*A−1=∣A∣1A∗
- λ−1α=(1∣A∣A∗)α\lambda^{-1}\alpha=(\frac{1}{|A|}A^*)\alphaλ−1α=(∣A∣1A∗)α
- ∣A∣λα=(A∗)α\frac{|A|}{\lambda}\alpha=(A^*)\alphaλ∣A∣α=(A∗)α
- (A∗)α=∣A∣λα(A^*)\alpha=\frac{|A|}{\lambda}\alpha(A∗)α=λ∣A∣α
- λ−1α=A−1α\lambda^{-1}\alpha=A^{-1}\alphaλ−1α=A−1α
-
-
推论:
- 特征向量不是被特征值所唯一确定的
- 特征值被特征向量唯一确定(一个特征向量只能属于一个特征值)
- 假设对于给定的α0\alpha_0α0,λ1,λ2,A\lambda_1,\lambda_2,Aλ1,λ2,A间满足:Aα0=λiα0,i=1,2A\alpha_0=\lambda_i\alpha_0,i=1,2Aα0=λiα0,i=1,2
- 因此λ1α0=λ2α0=Aα0\lambda_1\alpha_0=\lambda_2\alpha_0=A\alpha_0λ1α0=λ2α0=Aα0
- (λ1−λ2)α0=0(\lambda_1-\lambda_2)\alpha_0=0(λ1−λ2)α0=0
- 又因为α0≠0\alpha_0\neq{0}α0=0,所以λ1−λ2=0\lambda_1-\lambda_2=0λ1−λ2=0
- 所以λ1=λ2\lambda_1=\lambda_2λ1=λ2
- 所以给定α0\alpha_0α0,A的特征值是唯一确定的
- 假设对于给定的α0\alpha_0α0,λ1,λ2,A\lambda_1,\lambda_2,Aλ1,λ2,A间满足:Aα0=λiα0,i=1,2A\alpha_0=\lambda_i\alpha_0,i=1,2Aα0=λiα0,i=1,2
转置和特征值
-
方阵A的转置ATA^TAT的特征值和A的特征值相同
-
A:f(λ)=∣λE−A∣A:f(\lambda)=|\lambda{E}-A|A:f(λ)=∣λE−A∣
-
AT:f(λ)=∣λE−AT∣=∣(λE)T−AT∣=∣(λE−A)T∣=∣λE−A∣A^T:f(\lambda)=|\lambda{E}-A^T|=|(\lambda{E})^T-A^T|=|(\lambda{E}-A)^T|=|\lambda{E}-A|AT:f(λ)=∣λE−AT∣=∣(λE)T−AT∣=∣(λE−A)T∣=∣λE−A∣
-
可见,A,ATA,A^TA,AT具有相同的特征方程,因此特征值一定像相同
-
但是它们的特征向量不一定相同
- 因为前面我们讨论过,特征值不能够唯一确定特征向量
-
其他结论(方阵多项式的特征值与方阵本身特征值的关系)
-
设p(x)=∑i=0maixi=∑i=0mam−ixm−ip(x)=\sum\limits_{i=0}^{m}a_{i}x^i=\sum\limits_{i=0}^{m}a_{m-i}x^{m-i}p(x)=i=0∑maixi=i=0∑mam−ixm−i
- λ,A,α\lambda,A,\alphaλ,A,α满足Aα=λαA\alpha=\lambda\alphaAα=λα
- 则p(A)α=p(λ)αp(A)\alpha=p(\lambda)\alphap(A)α=p(λ)α
-
证明:
- p(A)α=∑i=0maiAiα=∑i=0maiλiα而p(λ)=∑i=0maiλi从而p(λ)α=∑i=0maiλiα因此p(A)α=p(λ)αp(A)\alpha=\sum\limits_{i=0}^{m}a_{i}A^i\alpha =\sum\limits_{i=0}^{m}a_{i}\lambda^i\alpha \\ 而p(\lambda)=\sum\limits_{i=0}^{m}a_{i}\lambda^i \\从而p(\lambda)\alpha=\sum\limits_{i=0}^{m}a_{i}\lambda^i\alpha \\ 因此p(A)\alpha=p(\lambda)\alpha p(A)α=i=0∑maiAiα=i=0∑maiλiα而p(λ)=i=0∑maiλi从而p(λ)α=i=0∑maiλiα因此p(A)α=p(λ)α
特征向量线性相关性
-
设n阶方阵A的特征向量为λi,i=1,2,⋯,n\lambda_i,i=1,2,\cdots,nλi,i=1,2,⋯,n,(λi≠λj\lambda_i\neq{\lambda_{j}}\,λi=λjif i≠ji\neq{j}i=j)
- 对应的特征向量为αi,i=1,2,⋯,n\alpha_i,i=1,2,\cdots,nαi,i=1,2,⋯,n
- 即:Aαi=λiαi,i=1,2,⋯,nA\alpha_i=\lambda_i\alpha_i,i=1,2,\cdots,nAαi=λiαi,i=1,2,⋯,n
- 那么ϕ=α1,⋯,αn\phi=\alpha_1,\cdots,\alpha_nϕ=α1,⋯,αn线性无关
- 通过数学归纳法证明
- 更一般的,设ψi=αi1,αi2,⋯,αisi\Large\psi_i=\alpha_{i1},\alpha_{i2},\cdots,\alpha_{is_i}ψi=αi1,αi2,⋯,αisi,αi∈{ψi}\alpha_i\in\{\psi_i\}αi∈{ψi}
- ψi\psi_iψi是同一个特征值λi\lambda_iλi的所有特征向量
- Ψ=ψ1,ψ2,⋯,ψn\Psi=\psi_1,\psi_2,\cdots,\psi_nΨ=ψ1,ψ2,⋯,ψn依然线性无关
- 对于ψi\psi_iψi:
- 若λi\lambda_iλi是一个k重特征值
- 那么对应于λi\lambda_iλi线性无关特征向量的个数u⩽ku\leqslant{k}u⩽k
相关文章:

LA@特征值和特征向量
文章目录特征值和特征向量例例求解方阵的特征值和特征向量🎈特征多项式特征方程方阵特征值和特征向量的性质证明推论衍生特征值更一般的转置和特征值其他结论(方阵多项式的特征值与方阵本身特征值的关系)特征向量线性相关性特征值和特征向量 许多定量分析模型中,常常…...
transpose代码学习
论文:TransPose: Keypoint Localization via Transformer Sen Yang Zhibin Quan Mu Nie Wankou Yang* School of Automation, Southeast University, Nanjing 210096, China {yangsenius, 101101872, niemu, wkyang}seu.edu.cn 下载地址:https://arxiv.o…...
【Redis】Redis 常用数据类型操作 ② ( 数据库操作 | 切换数据库 | 查询当前数据库键个数 | 清空当前数据库 | 清空所有数据库 )
文章目录一、Redis 数据库操作1、切换数据库2、查询当前数据库键个数3、清空当前数据库4、清空所有数据库一、Redis 数据库操作 在之前的博客 【Redis】Redis 数据库 安装、配置、访问 ( Redis 简介 | 下载 Redis 安装包 | 安装 Redis 数据库 | 命令行访问 Redis | 使用可视化工…...
最简单的物体识别例子
第一步下载百度EASYDL工具。 网址EasyDL 图像 然后下载本地训练工具包: 本地下载,运行。 首先创建数据集, 完成,创建目标任务。 选择物体检测创建任务 选择训练,将数据集引入 通用型小型设备SDK 选择这个可以本地直…...

指针——“C”
各位CSDN的uu们你们好呀,今天,小雅兰学习的内容是指针,这次只会讲一些很简单的知识点,更详细的指针知识会在以后的博客中逐步剖析清楚,那么现在,就让我们进入指针的世界吧 指针是什么 指针和指针类型 野指…...

学习 Linux 内核书籍推荐
原文链接,欢迎关注: 你为什么学习 Linux 内核? - CodeAllen的回答 - 知乎 https://www.zhihu.com/question/31369673/answer/2894981254 主要是工作需要,其实对于我自己的工作来说,在Linux开发的具体业务和算法才是重…...

深圳硬件黑客松活动,开放报名!
开源社KAIYUANSHE近期微信公众号订阅功能做调整啦!没有被星标的账号在信息流里可能不显示大图了!快星标⭐我们,就可以及时看到发布的文章啦!STEP01 点击右上角标志STEP02 点击【设为星标】近年来,创客文化越来越受到人…...

力扣sql简单篇练习(十七)
力扣sql简单篇练习(十七) 1 销售分析| 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 可以考虑使用all函数 SELECT seller_id FROM Sales GROUP BY seller_id HAVING sum(price)>all(SELECT sum(price)FROM SalesGROUP BY seller_id )1.3 运行…...
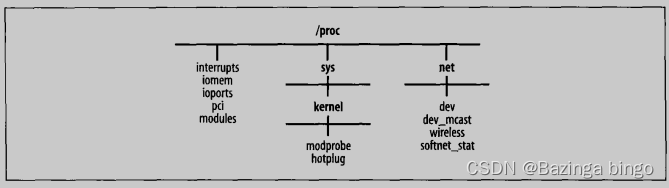
Linux网络技术学习(六)—— 网络设备初始化(II)
文章目录初始化选项模块选项设备处理层初始化:net_dev_init用户空间辅助程序kmod解析热插拔虚拟设备虚拟设备范例通过/proc文件系统调整初始化选项 内核内建的组件以及模块加载的组件都能输入参数,使用户调整组件所实现的功能、重写默认值等 模块选项&…...
一手教你如何搭建Hadoop基于Zookeeper的集群(5台主机)
文章目录一、设计集群图二、准备五台虚拟机2.1、下载安装文件2.2、创建虚拟机2.3、配置网络2.4、修改主机名称2.5、关闭防火墙2.6、同步时间2.7、设置/etc/hosts文件2.8、设置免密登录2.9、为后面可以主备替换安装psmisc三、安装JDK3.1、安装jdk3.2、测试jdk是否安装成功3.3、将…...

Spring Cloud是什么?怎么理解Spring Cloud?
简介Spring Cloud项目的官方网址:https://projects.spring.io/spring-cloud/ Spring Cloud 并不是一个项目,而是一组项目的集合。在 Spring Cloud中包含了很多的子项目,每一个子项目都是一种微服务开发过程中遇到的问题的一种解决方案。它利…...

robotframework + selenium自动化测试常见的问题
1、 插入中文数据提示 FAIL UnicodeEncodeError: ‘latin-1’ codec can’t encode characters in position 92-107: ordinal not in range(25 DataBaseLibrary插入中文乱码的解决:修改D:\Python27\Lib\site-packages\DatabaseLibrary\connection_manager.py里的co…...
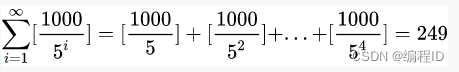
2023春招java面试题及答案
2023春招java面试题及答案总结1.以下Dubbo服务负载均衡策略中,哪一个策略的功能是相同参数的请求总是发到同一个提供者()2.如下代码:请问编译运行的结果是什么?3.给出如下代码:请问编译运行的结果是什么&am…...

QT+OpenGL光照
QTOpenGL光照 本篇完整工程见gitee:QtOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主 颜色 现实生活中看到的物体的颜色并不是这个物体真正拥有的颜色,而是它所反射的颜色 太阳光能被看见的白光是多找演的的组合…...

OpenCV-PyQT项目实战(7)项目案例03:鼠标框选
欢迎关注『OpenCV-PyQT项目实战 Youcans』系列,持续更新中 OpenCV-PyQT项目实战(1)安装与环境配置 OpenCV-PyQT项目实战(2)QtDesigner 和 PyUIC 快速入门 OpenCV-PyQT项目实战(3)信号与槽机制 …...
)
vue2版本《后台管理模式》(上)
后台管理模式项目开发经验总结如下,希望对你们有些帮助: 文章目录一、app 出口位置二 、 index.js 路由配置三、package.json 文件四、 main.js 既然安装插件那就需要引入五、 跨域问题总结首先需要一个完整的v2版本的项目 vue2版本思路:首先…...

C++与C基础重叠部分
Cmake CPP程序开发过程 计算机硬件—>机器语言—>汇编—>cppcpp—>机器(gcc)Make(makefile)—>本地智能批处理翻译机制Cmake—>跨平台生成不同设备上的makefile进行执行 Cpp基础学习 基本知识 基本格式 #include<iostream> using namespace std;…...

神经网络基础部件-卷积层详解
前言 在全连接层构成的多层感知机网络中,我们要通过将图像数据展平成一维向量来送入模型,但这会忽略了每个图像的空间结构信息。理想的策略应该是要利用相近像素之间的相互关联性,将图像数据二维矩阵送给模型中学习。 卷积神经网络(convolu…...
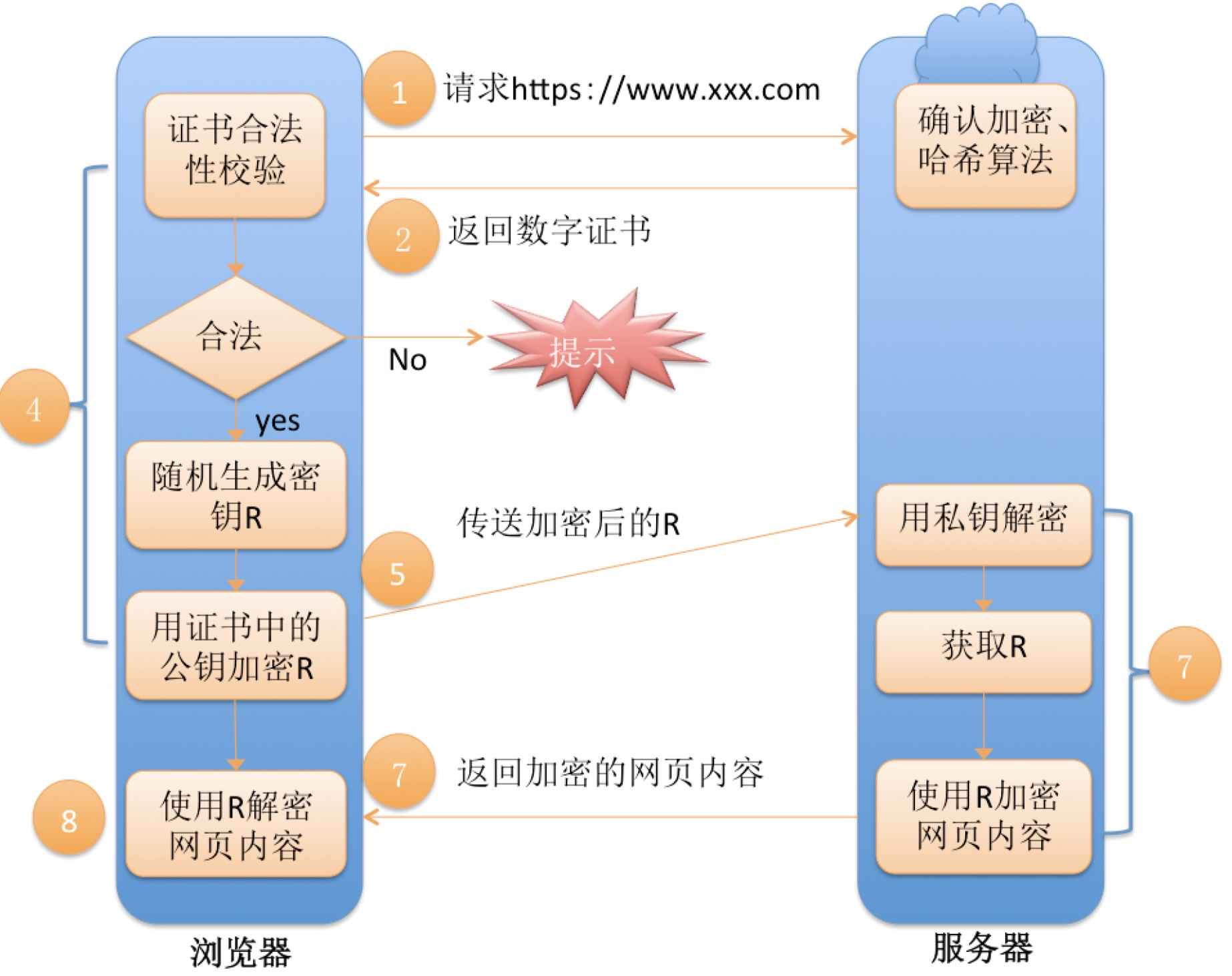
【计算机网络】HTTPS协议原理
文章目录一、认识HTTPS协议二、为什么要发明HTTPS三、HTTP与HTTPS的区别四、常见的加密方式1. 对称加密2. 非对称加密3. 数据摘要4. 数字签名五、HTTPS的原理探究方案1:只使用对称加密方案2:只使用非对称加密方案3:双方都使用非对称加密方案4…...

21岁,华科博士在读,我的赛事Top经验
Datawhale干货 作者:vaew,华中科技大学,博士二年级在读简介笔者vaew,21岁,现为华中科技大学机械科学与工程学院陶波教授课题组博士二年级学生。主要研究方向是基于视触融合的机器人灵巧操作。学业之余的研究兴趣包括图…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
