数仓理论【范式】【维度建模】
数仓理论
1 范式理论
1.1 范式概念
数据建模要遵循一定的规则,在关系建模中,这种规则就是范式
采用范式结构,可以有效的降低数据的冗余性
范式在获取数据时,需要通过join拼接出数据
范式有第一范式(1NF),第二范式(2NF),第三范式(3NF),巴斯-科德范式(BCNF),第四范式(4NF),第五范式(5NF)
一般只遵循到第三范式
1.2 函数依赖
1.2.1 完全函数依赖
通过(学号,课程)可以推断出分数,但是单独用学号或者课程都不能推断出分数,这时可以说分数完全依赖于(学号,课程)
即AB能推断出C,但是A和B单独不能推断出C,这时C完全依赖于AB
1.2.2 部分函数依赖
通过(学号,课程)可以推断出姓名,但是只通过学号就能推断出姓名,这时可以说姓名部分依赖于(学号,课程)
即AB能得出C,A或B单独也能得出C,这时C部分依赖于AB
1.2.3 传递函数依赖
学号可以推断出学院名,学院名可以推断出院长,但是院长推断不出来学号,这时可以说院长传递依赖于学号
即A得出B,B得出C,但是C得不到A,这时C传递依赖于A
1.3三范式的区分
1.3.1 第一范式
1NF的核心原则为:属性不可切割
比如下面的表格,商品列中的数据可以分割成 3台 和 电脑 ,所以下面的表格不遵循1NF
| 商品ID | 商品 | 商家ID | 用户ID |
|---|---|---|---|
| 001 | 3台电脑 | 001 | 001 |
修改成遵循1NF的表格为
| 商品ID | 商品 | 商家ID | 用户ID | 数量 |
|---|---|---|---|---|
| 001 | 电脑 | 001 | 001 | 3 |
1NF时关系型数据库的最基本的要求,在RDBMS中创建表时,如果不符合1NF的要求,操作是不会成功的
1.3.2 第二范式
2NF的原则为:不存在部分函数依赖
比如下面的表格,属性不可切割,满足第一范式,但是课名不完全依赖于(学号,姓名),所以不满足2NF的要求
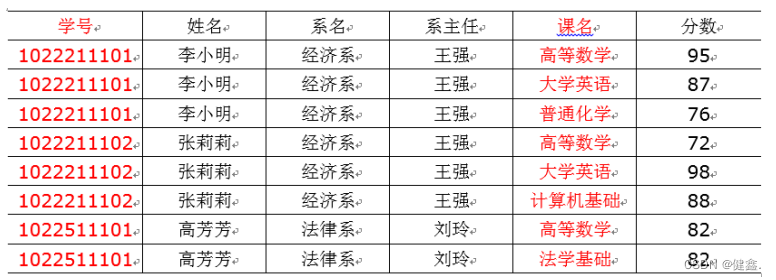
这时将表拆分成以下两个,这时就满足了2NF


1.3.3 第三范式
3NF的原则为:不存在传递函数依赖
拿上面满足2NF的第二章表来说,系主任传递依赖于学号,所以需要进行进一步的拆解
拆分之后的如下两张表满足3NF
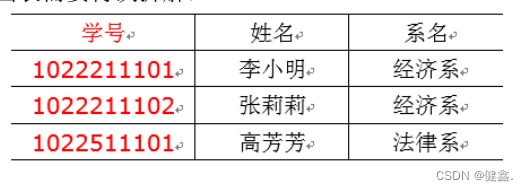

2 关系建模和维度建模
2.2 关系建模
关系建模将数据抽象成两个概念:实体和关系,使用规范化的方式表示出来,如图所示,关系建模较为松散。

关系建模遵循三范式,数据冗余性低,但是查询相对复杂,join操作比较多导致MR较多,查询效率较低
2.3 维度建模
维度建模以数据分析为出发点,不遵循三范式,存在一些数据冗余
面向业务,将业务用事实表和维度表的方式表现出来
查询效率较高

3 维度表和事实表
3.1 维度表
维度表一般是对事实的描述信息,比如:用户、商品、日期等
维度表很宽,具有多个属性,列多
与事实表相比,行数相对较小
内容相对固定
- 比如:时间维度表
| 日期ID | day of week | day of year | 季度 |
|---|---|---|---|
| 2023-2-15 | 3 | 46 | 1 |
| 2023-2-16 | 4 | 47 | 1 |
3.2 事实表
事实表中每行数据代表了一个业务事件(下单,支付等)
实时表示的是实践的度量值(次数,个数,金额等)
比如:2023年2月15日,jx在京东花了40元买了一本书
维度表存储:时间、用户、商家、商品等
实时表存储:数量、价钱(40元,一本)
一个事实表的行包括:度量值、与维度表相连的外键(通常有多个外键)
事实表非常大,相对较窄,列数较少,主要存储的是外键id和度量值
经常会发生变化,会产生很多的新增数据
3.2.1 事务型事实表
以单个事务或时间为单位
比如:一笔支付记录、一个订单记录
事实表中的一行数据,一旦事务被提交,数据被插入,就不能在进行更改
更新方式为增量同步
3.2.2 周期型快照事实表
不会保留所有的数据,只保留固定时间间隔的数据
比如:每天的营业额、每月的账户余额等
再比如:购物车随时都有可能增减商品,但是只关心每天结束时购物车的情况
3.2.3 累积型快照事实表
用于跟踪业务事实的变化
比如:要累积订单从下单开始,到订单商品打包、运输、签收的各个业务阶段的数据来追踪进展情况
这个业务进行时,事实表的记录也要不断更新
4 维度模型的分类
4.1 模型的介绍
维度模型分为三种:星型模型、雪花模型、星座模型
- 星型模型
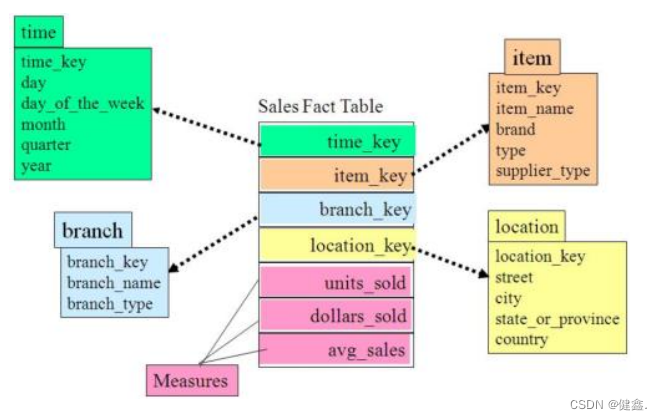
标准的星型模型只有一层
- 雪花模型
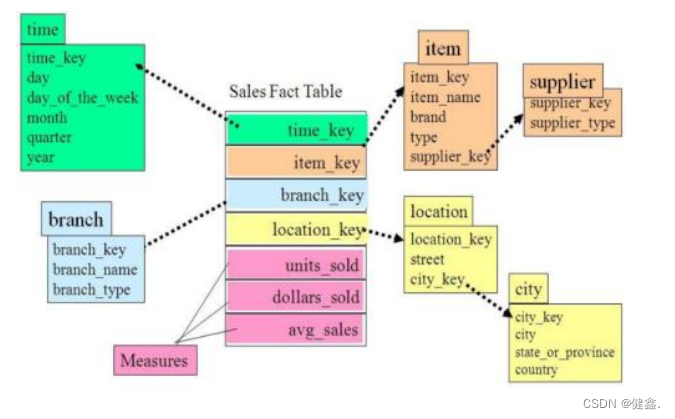
雪花模型和星型模型的区别主要在于维度的层级
雪花模型较为靠近3NF,但是无法完全遵守
- 星座模型

星座模型包含多个事实表,多个事实表共享维度表
多个星型模型或者雪花模型会形成星座模型
4.2 模型的选择
星座模型不用进行原则,多个事实表共享维度表是正常的,是数据仓库的常态
选择星型模型还是雪花模型,取决于是性能优先还是灵活优先,在实际的开发中不会只选择一种,需要根据情况灵活组合
星型模型维度更少,可以减少join,进而减少shuffle
相关文章:

数仓理论【范式】【维度建模】
数仓理论 1 范式理论 1.1 范式概念 数据建模要遵循一定的规则,在关系建模中,这种规则就是范式 采用范式结构,可以有效的降低数据的冗余性 范式在获取数据时,需要通过join拼接出数据 范式有第一范式(1NF),第二范式…...
卷积神经网络
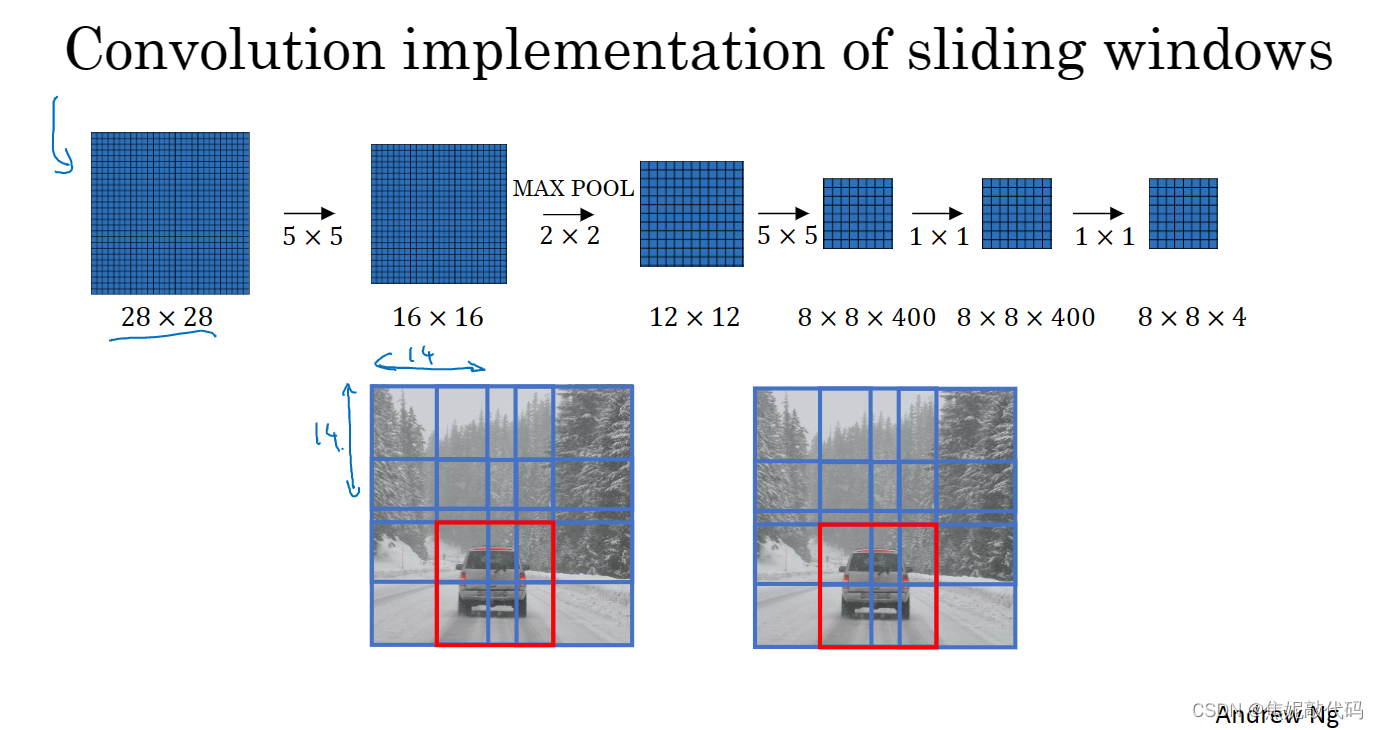
卷积神经网络1. 卷积神经网络边缘检测示例Padding卷积步长三维卷积单层卷积网络简单卷积网络示例池化层卷积神经网络示例2. 深度卷积网络经典网络残差网络残差网络为什么有用1 x 1 卷积谷歌Inception 网络介绍Inception 网络迁移学习数据扩充(数据增强)3…...
问题)
解决Qt提示xxx.so not found( using -rpath or -rpath-link)问题
问题描述: 在QtCreator中交叉编译的时候突然出现了以下动态库找不到的问题: 我这里是aarch64,其他环境类似即可。 /usr/lib/gcc-cross/aarch64-linux-gnu/7/../../../../aarch64-linux-gnu/bin/ld: warning: libwrap.so.0, needed by /home.../../nfsdir///libpulsecommo…...

Blazor 托管模型 BlazorWebAssembly和Blazor Server
BlazorWebAssembly 应用 BlazorWebAssembly 应用使用基于 WebAssembly 的 .NET 运行时在浏览器中直接执行。 BlazorWebAssembly 应用的工作方式类似于 Angular 和 React 等前端 JavaScript 框架。 但不是编写 JavaScript,而是编写 C#。 .NET 运行时与应用、应用程序…...

从未想过制作数据可视化展示竟可以如此简单
还在跟着网络上一节课好几个小时的付费课程学习如何制作数据可视化大屏嘛?还在为不知道怎么设计数据展示排版而苦恼?今天教大家用最简单的方式制作一个数据可视化大屏,首先让我们看一下参考大屏样式:接下来我们将制作数据可视化大…...
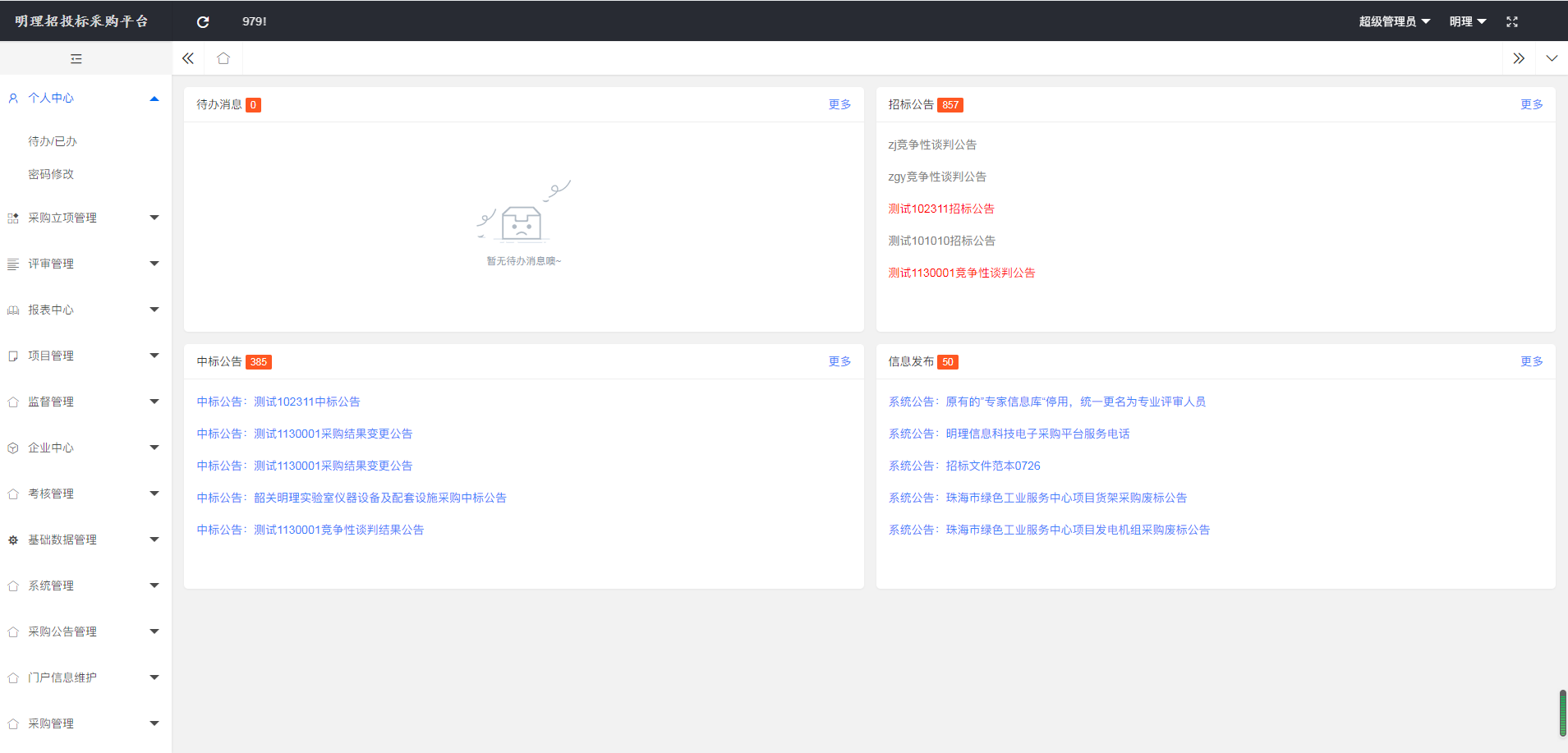
企业电子招投标采购系统源码之功能模块的描述
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外部供…...

LeetCode-2341. 数组能形成多少数对【哈希表,计数】
LeetCode-2341. 数组能形成多少数对【哈希表,计数】题目描述:解题思路一:哈希表,将数组中的数加入哈希表中,若有两个相同的数就记录下来,并消去两个。最后只需遍历哈希表中置为1的个数即可。解题思路二&…...
vue-echarts实现多功能图表
前言作为前端人员,日常图表、报表、地图的接触可谓相当频繁,今天小编隆重退出前端框架之VUE结合百度echart实现中国地图各种图表的展示与使用;作为“你值得拥有”专栏阶段性末篇,值得一看主要实现功能——中国地图——环形图——折…...

C#快键精灵
我发过挺多工作中用到的C#内容,整体链接和内容去这里看下:C#基础知识体系框架图,及起对应我发过的博客_花开莫与流年错_的博客-CSDN博客_c#架构图 可以记住电脑上鼠标、键盘操作记录,用处就很多,比较灵活了,…...

谷歌、微软、Meta?谁才是 Python 最大的金主?
你知道维护 Python 这个大规模的开源项目,每年需要多少资金吗? 答案是:约 200 万美元! PSF(Python 软件基金会)在 2022 年 6 月发布了 2021 的年度报告,其中披露了以下这份支出明细(…...

面向对象笔记
标准JavaBean类1.类名见名知意2.成员变量由private修饰3.提供两个构造方法 无参构造和带全部参数构造4.提供每一个成员变量对应的set/get方法5.如果有其它行为,也要写上空参构造 初始化默认值带参构造 初始化参数 创建对象由虚拟机调用,不能手动调用每创…...

tofu:一款功能强大的模块化Windows文件系统安全测试工具
关于tofu tofu是一款功能强大的针对Windows文件系统安全的模块化工具,该工具可以使用离线方法对目标Windows文件系统进行渗透测试,并通过绕过Windows系统登录界面来帮助广大研究人员测试Windows主机的安全性。除此之外,该工具还可以执行哈希…...
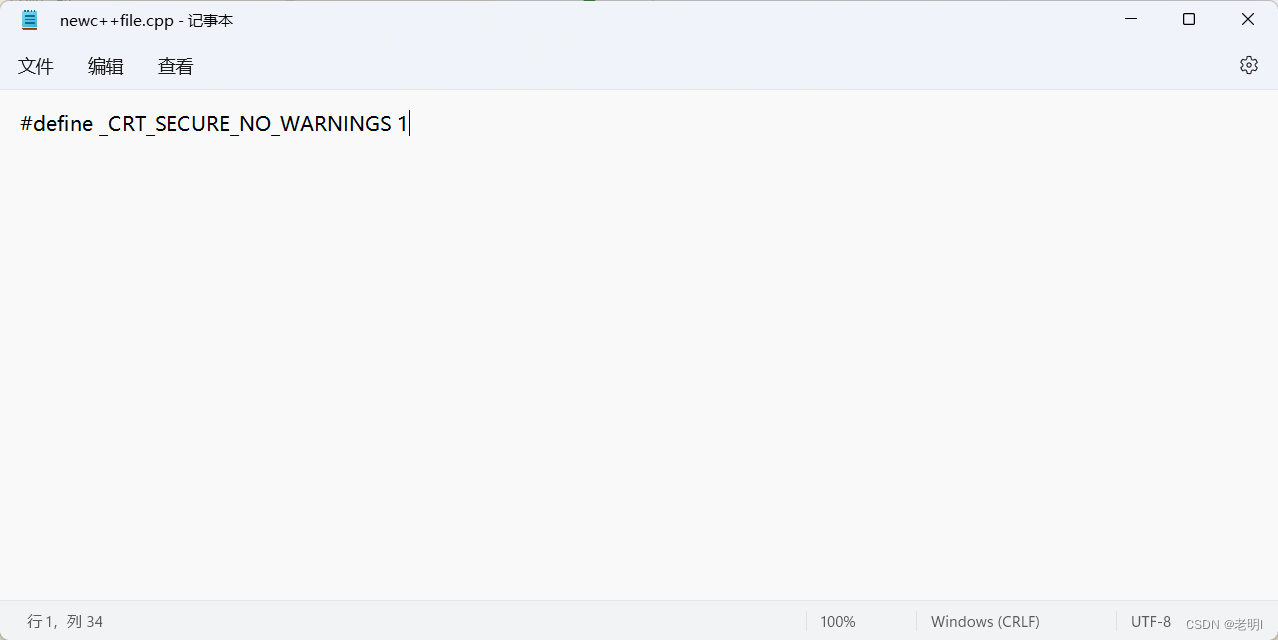
VS中scanf为什么会报错
简单来讲,scanf会强行输入内容,所以是不安全的。 我们来看这样的例子: #include <iostream> using namespace std;int main() {char demo[3];scanf("%s", demo);return 0; }对于以上代码,当我们输入字符不超过3时…...
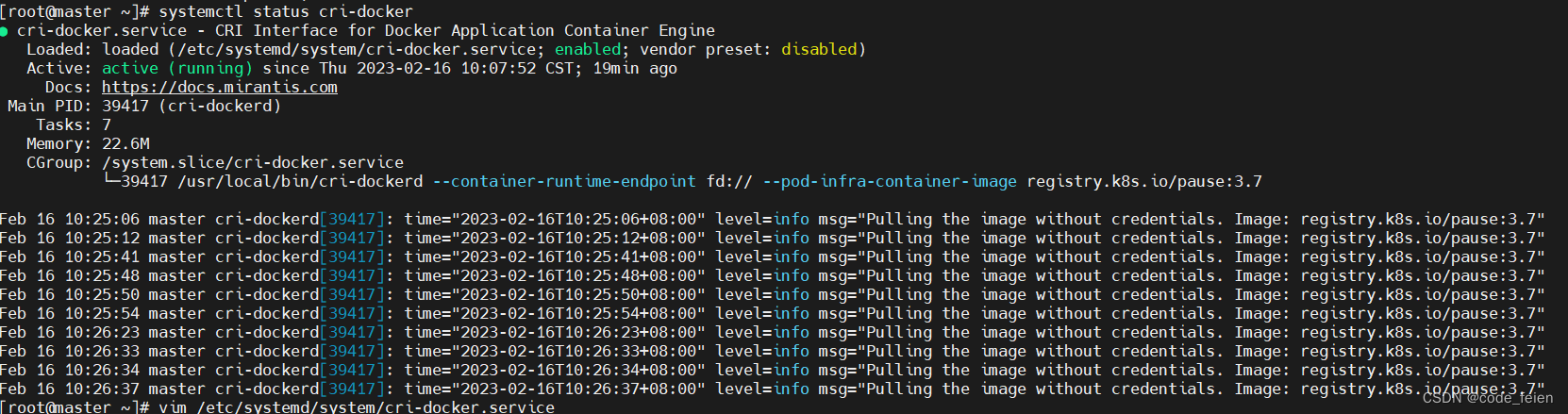
使用kubeadm部署k8s1.24.0版本,遇到的坑总结
使用kubeadm部署k8s1.24.0版本,遇到的坑总结环境安装遇到的问题环境 操作系统:centos7 内核:5.4.231-1.el7.elrepo.x86_64 kubeadm:1.24.0 kubelet:1.24.0 kubectl:1.24.0 cri:docker cni&…...

【C++】特殊类设计
🌈欢迎来到C专栏~~特殊类设计 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&a…...

中创教育PMP如何轻松应对公司90%以上的沟通难题
掌握沟通技能,可以让问题从1变成0; 掌握沟通技能,可以让机会从0变成1; 掌握沟通技能,可以让成功从1变成100; 难题一、当领导问你某件事,但你又不太清楚时 【说话公式】需要思考需要确认晚点回…...

#笨鸟先飞# 数据结构与算法基础 课程笔记 第六章 图
图的定义和基本术语图:G( V , E ) Graph(Vertex,Edge)V:顶点(数据元素)的有穷非空集合;E:边的有穷集合。无向图:每条边都是无方向的有向图:每条边…...

深入浅出带你学习Apache中间件常见漏洞
前言 上一篇文章给大家总结了一下IIS中间件的漏洞,这篇文章就给大家讲一下apache中间件漏洞,说起apache大家一定不会陌生,这是我们日常中经常用到的中间件,下面由我来给大家讲解一下改中间件常见的漏洞。 Apache是什么ÿ…...

用多种指针方法访问数据元素,实现逆序输出
这里注意下数组指针的下标表示: 我们已经知道,数组名a总是指向a[0]的指针,*(ai)是对a[i]的引用,实际上,编译器中,对数组的引用,如a[i],总是被编译器改写成*(ai)的形式。 另外说明下…...

WebDAV之葫芦儿·派盘+NMM
NMM 支持WebDAV方式连接葫芦儿派盘。 推荐一款文件管理器,可以对手机中的文件进行多方面的管理,支持语法高亮和ftp等远程的文件的管理。支持从WebDav服务器连接葫芦儿派盘服务下载文件和上传文件。 NMM文本编辑器是一款文件管理器,在功能上面更加的适合于一些编程人员进行使…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
