【算法 | 例题简答】相关例题讲解
目录
简答题
计算题
时间复杂度的计算
递归算法计算
背包问题(0-1背包问题)
回溯法
动态规划法
编程题
用回溯法解方程
动态规划法解决蜘蛛吃蚊子
用分治法解决抛硬币问题
用二分法分两边求最大值
简答题
1、什么是算法?算法有哪些特征?
算法是求解问题的一系列计算步骤。算法具有有限性、确定性、可行性、输入性和输出性。
2、什么是直接递归和间接递归?消除递归一般要用什么数据结构?
直接递归:一个 f 函数定义中直接调用 f 函数自己。
间接递归:一个 f 函数定义中调用 g 函数,而 g 函数的定义中调用 f 函数。消除递归一般要用栈实现。
3、分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题,分别解决子问题,最后将子问题的解组合起来形成原问题的解。这要求原问题和子问题:
问题规模不同,问题性质相同。
4、在寻找 n 个元素中第 k 小元素问题中,如快速排序算法思想,运用分治算法对 n个元素进行划分,如何选择划分基准?
随机选择一个元素作为划分基准、取子序列的第一个元素作为划分基准、用中位数的中位数方法寻找划分基准。
5、快速排序算法是根据分治策略来设计的,简述其基本思想。
对于无序序列 a[low..high]进行快速排序,整个排序为“大问题”。选择其中的一个基准 base=a[i](通常以序列中第一个元素为基准),将所有小于等于 base 的元素移动到它的前面,所有大于等于 base 的元素移动到它的后面,即将基准归位到 a[i],这样产生a[low..i-1]和 a[i+1..high]两个无序序列,它们的排序为“小问题”。当 a[low..high]序列只有一个元素或者为空时对应递归出口。
所以快速排序算法就是采用分治策略,将一个“大问题”分解为两个“小问题”来求解。由于元素都是在 a 数组中,其合并过程是自然产生的,不需要特别设计。
6、假设含有 n 个元素的待排序的数据 a 恰好是递减排列的,说明调用 QuickSort(a,0,n-1)递增排序的时间复杂度为 O(
)。
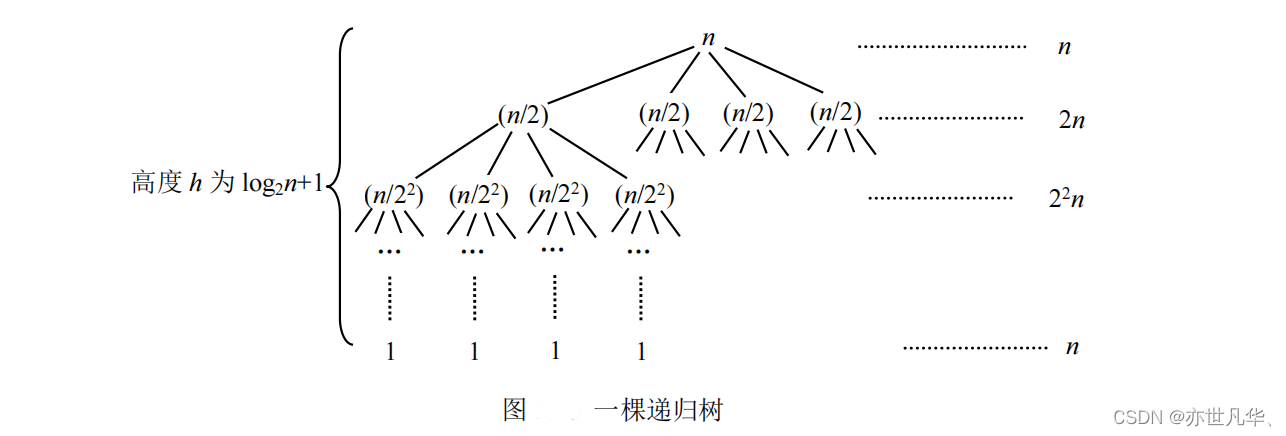
此时快速排序对应的递归树高度为 O(n),每一次划分对应的时间为 O(n),以整个排序时间为 O()。
7、哪些算法采用分治策略。
其中二路归并排序和折半查找算法采用分治策略。
8、适合并行计算的问题通常表现出哪些特征?
1)将工作分离成离散部分,有助于同时解决。例如,对于分治法设计的串行算法,可以将各个独立的子问题并行求解,最后合并成整个问题的解,从而转化为并行算法。
2)随时并及时地执行多个程序指令。
3)多计算资源下解决问题的耗时要少于单个计算资源下的耗时。
9、设有两个复数 x=a+bi 和 y=c+di。复数乘积 xy 可以使用 4 次乘法来完成,即xy=(ac-bd)+(ad+bc)i。设计一个仅用 3 次乘法来计算乘积 xy 的方法。
xy=(ac-bd)+((a+b)(c+d)-ac-bd)i。由此可见,这样计算 xy 只需要 3 次乘法(即ac、bd 和(a+b)(c+d)乘法运算)。
10、 有 4 个数组 a、b、c 和 d,都已经排好序,说明找出这 4 个数组的交集的方法。
采用基本的二路归并思路,先求出 a、b 的交集 ab,再求出 c、d 的交集 cd,最后求出 ab 和 cd 的交集,即为最后的结果。也可以直接采用 4 路归并方法求解。
11、简要比较蛮力法和分治法。
蛮力法是一种简单直接地解决问题的方法,适用范围广,是能解决几乎所有问题的一般性方法,常用于一些非常基本、但又十分重要的算法(排序、查找、矩阵乘法和字符串匹配等),蛮力法主要解决一些规模小或价值低的问题,可以作为同样问题的更高效算法的一个标准。而分治法采用分而治之思路,把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题直到问题解决。分治法在求解问题时,通常性能比蛮力法好。
12、在采用蛮力法求解时什么情况下使用递归?
如果用蛮力法求解的问题可以分解为若干个规模较小的相似子问题,此时可以采用递归来实现算法
13、回溯法在问题的解空间树中,按什么策略,从根结点出发搜索解空间树?
深度优先
14、对于回溯法说法错误的是
回溯算法需要借助队列这种结构来保存从根结点到当前扩展结点的路径
15、回溯法的效率依赖于哪些因素?
满足显约束的值的个数、计算约束函数的时间、计算限界函数的时间
16、什么函数是回溯法中为避免无效搜索采取的策略?
剪枝函数
17、回溯法的搜索特点是什么?
回溯法在解空间树中采用深度优先遍历方式进行解搜索,即用约束条件和限界函数考察解向量元素 x[i]的取值,如果 x[i]是合理的就搜索 x[i]为根结点的子树,如果x[i]取完了所有的值,便回溯到 x[i-1]。
18、用回溯法解 0/1 背包问题时,该问题的解空间是何种结构?用回溯法解流水作业调
度问题时,该问题的解空间是何种结构?
用回溯法解 0/1 背包问题时,该问题的解空间是子集树结构。用回溯法解流水作业调度问题时,该问题的解空间是排列树结构。
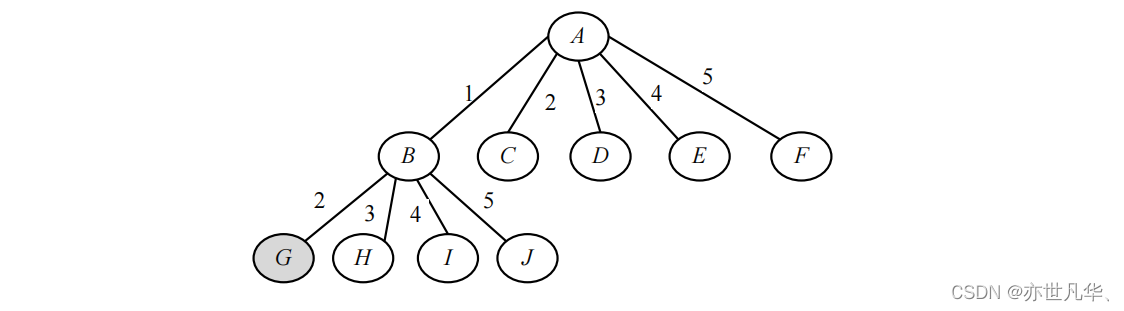
19、对于递增序列 a[]={1,2,3,4,5},采用回溯法求全排列,以 1、2 开头的排列一定最先出现吗?为什么?
是的。对应的解空间是一棵排列树,如图所示给出前面 3 层部分,显然最先产生的排列是从 G 结点扩展出来的叶子结点,它们就是以 1、2 开头的排列。
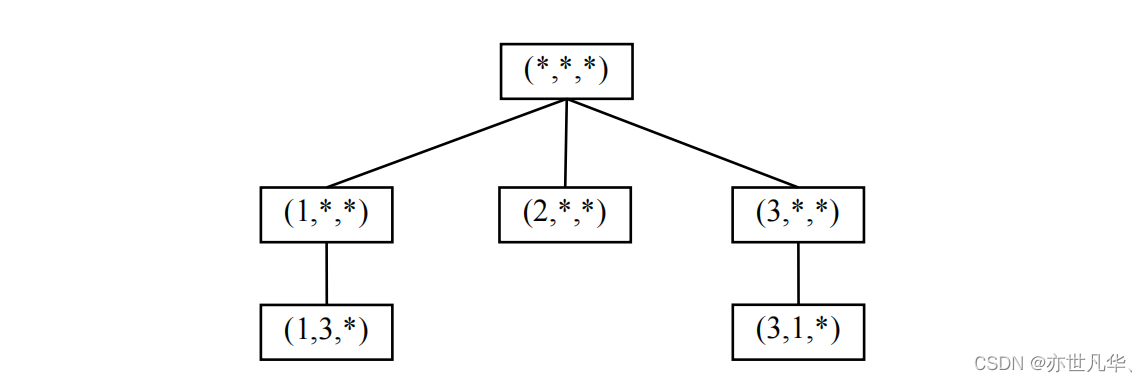
20、考虑 n 皇后问题,其解空间树为由 1、2、…、n 构成的 n!种排列所组成。现用回溯法求解,如下:
(1)通过解搜索空间说明 n=3 时是无解的。
n=3 时的解搜索空间如图所示,不能得到任何叶子结点,所有无解。
(2)给出剪枝操作。
剪枝操作是任何两个皇后不能同行、同列和同两条对角线。
(3)最坏情况下在解空间树上会生成多少个结点?分析算法的时间复杂度。
最坏情况下每个结点扩展 n 个结点,共有个结点,算法的时间复杂度为O(
)
21、分枝限界法在问题的解空间树中,按什么策略,从根结点出发搜索解空间树。
广度优先
22、常见的两种分枝限界法为:
队列式(FIFO)分枝限界法与优先队列式分枝限界法。
23、分枝限界法求解 0/1 背包问题时,活结点表的组织形式是
大根堆
24、采用最大效益优先搜索方式的算法是
分枝限界法
25、优先队列式分枝限界法选取扩展结点的原则是
结点的优先级
26、简述分枝限界法的搜索策略。
分枝限界法的搜索策略是广度优先遍历,通过限界函数可以快速找到一个解或者最优解。
27、有一个 0/1 背包问题,其中 n=4,物品重量为(4,7,5,3),物品价值为(40,42,25,12),背包最大载重量 W=10,给出采用优先队列式分枝限界法求最优解的过程。
求解过程如下:
1)根结点 1 进队,对应结点值:e.i=0,e.w=0,e.v=0,e.ub=76,x:[0,0,0,0]。
2)出队结点 1:左孩子结点 2 进队,对应结点值:e.no=2,e.i=1,e.w=4,e.v=40,e.ub=76,x:[1,0,0,0];右孩子结点 3 进队,对应结点值:e.no=3,e.i=1,
e.w=0,e.v=0,e.ub=57,x:[0,0,0,0]。
3)出队结点 2:左孩子超重;右孩子结点 4 进队,对应结点值:e.no=4,e.i=2,e.w=4,e.v=40,e.ub=69,x:[1,0,0,0]。
4)出队结点 4:左孩子结点 5 进队,对应结点值:e.no=5,e.i=3,e.w=9,e.v=65,e.ub=69,x:[1,0,1,0];右孩子结点 6 进队,对应结点值:e.no=6,e.i=3,e.w=4,e.v=40,e.ub=52,x:[1,0,0,0]。
5)出队结点 5:产生一个解,maxv= 65,bestx:[1,0,1,0]。
6)出队结点 3:左孩子结点 8 进队,对应结点值:e.no=8,e.i=2,e.w=7,e.v=42,e.ub=57,x:[0,1,0,0];右孩子结点 9 被剪枝。
7)出队结点 8:左孩子超重;右孩子结点 10 被剪枝。
8)出队结点 6:左孩子结点 11 超重;右孩子结点 12 被剪枝。
9)队列空,算法结束,产生的最优解:maxv= 65,bestx:[1,0,1,0]。
28、有一个流水作业调度问题,n=4,a[]={5,10,9,7},b[]={7,5,9,8},给出采用优先队列式分枝限界法求一个解的过程。
求解过程如下:
1)根结点 1 进队,对应结点值:e.i=0,e.f1=0,e.f2=0,e.lb=29, x:[0,0,0,0]。
2)出队结点 1:扩展结点如下:
进队(j=1):结点 2,e.i=1,e.f1=5,e.f2=12,e.lb=27,x:[1,0,0,0]。
进队(j=2):结点 3,e.i=1,e.f1=10,e.f2=15,e.lb=34,x:[2,0,0,0]。
进队(j=3):结点 4,e.i=1,e.f1=9,e.f2=18,e.lb=29,x:[3,0,0,0]。
进队(j=4):结点 5,e.i=1,e.f1=7,e.f2=15,e.lb=28,x:[4,0,0,0]。
3)出队结点 2:扩展结点如下:
进队(j=2):结点 6,e.i=2,e.f1=15,e.f2=20,e.lb=32,x:[1,2,0,0]。
进队(j=3):结点 7,e.i=2,e.f1=14,e.f2=23,e.lb=27,x:[1,3,0,0]。
进队(j=4):结点 8,e.i=2,e.f1=12,e.f2=20,e.lb=26,x:[1,4,0,0]。
4)出队结点 8:扩展结点如下:
进队(j=2):结点 9,e.i=3,e.f1=22,e.f2=27,e.lb=31,x:[1,4,2,0]。
进队(j=3):结点 10,e.i=3,e.f1=21,e.f2=30,e.lb=26,x:[1,4,3,0]。
5)出队结点 10,扩展一个 j=2 的子结点,有 e.i=4,到达叶子结点,产生的一个解
是 e.f1=31,e.f2=36,e.lb=31,x=[1,4,3,2]。
该解对应的调度方案是:第 1 步执行作业 1,第 2 步执行作业 4,第 3 步执行作业
3,第 4 步执行作业 2,总时间=36。
29、贪心算法的基本要素的是
贪心选择性质
30、什么问题不能使用贪心法解决。
n 皇后问题
31、采用贪心算法的最优装载问题的主要计算量在于将集装箱依其重量从小到大排序,故算法的时间复杂度为
O(nlog2n)
32、关于 0/ 1 背包问题
对于同一背包与相同的物品,做背包问题取得的总价值一定大于等于做 0/1 背包问题。
33、一棵哈夫曼树共有 215 个结点,对其进行哈夫曼编码,共能得到( )个不同的码字。
108
34、求解哈夫曼编码中如何体现贪心思路?
在构造哈夫曼树时每次都是将两棵根结点最小的树合并,从而体现贪心的思路。
35、举反例证明 0/1 背包问题若使用的算法是按照 vi/wi的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解(此题说明 0/1 背包问题与背包问题的不同)。
例如,n=3,w={3,2,2},v={7,4,4},W=4 时,由于 7/3 最大,若按题目要求的方法,只能取第一个,收益是 7。而此实例的最大的收益应该是 8,取第 2、3个物品。
36、通常以自底向上的方式求解最优解的是
动态规划法
37、备忘录方法是什么算法的变形。
动态规划法
38、动态规划算法基本要素的是。
子问题重叠性质
39、一个问题可用动态规划算法或贪心算法求解的关键特征是问题的:
最优子结构性质
40、简述动态规划法的基本思路。
动态规划法的基本思路是将待求解问题分解成若干个子问题,先求子问题的解,然后从这些子问题的解得到原问题的解。
41、简述动态规划法与贪心法的异同。
动态规划法的 3 个基本要素是最优子结构性质、无后效性和重叠子问题性质,而贪心法的两个基本要素是贪心选择性质和最优子结构性质。所以两者的共同点是都要求问题具有最优子结构性质。
两者的不同点如下:
(1)求解方式不同,动态规划法是自底向上的,有些具有最优子结构性质的问题只能用动态规划法,有些可用贪心法。而贪心法是自顶向下的。
(2)对子问题的依赖不同,动态规划法依赖于各子问题的解,所以应使各子问题最优,才能保证整体最优;而贪心法依赖于过去所作过的选择,但决不依赖于将来的选择,也不依赖于子问题的解。
42、简述动态规划法与分治法的异同。
两者的共同点:
是将待求解的问题分解成若干子问题,先求解子问题,然后再从这些子问题的解得到原问题的解。
两者的不同点是:
适合于用动态规划法求解的问题,分解得到的各子问题往往不是相互独立的(重叠子问题性质),而分治法中子问题相互独立;另外动态规划法用表保存已求解过的子问题的解,再次碰到同样的子问题时不必重新求解,而只需查询答案,故可获得多项式级时间复杂度,效率较高,而分治法中对于每次出现的子问题均求解,导致同样的子问题被反复求解,故产生指数增长的时间复杂度,效率较低
43、哪些属于动态规划算法?
判断算法是否具有最优子结构性质、无后效性和重叠子问题性质。直接插入排序算法、简单选择排序算法 和 二路归并排序算法 均属于动态规划算法。
计算题
时间复杂度的计算
一、


二、

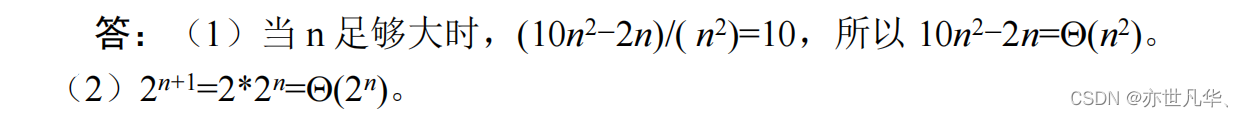
三、
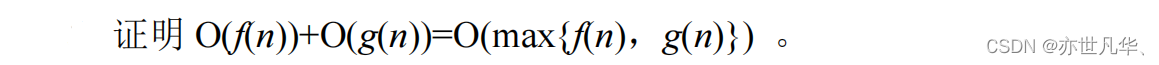

递归算法计算
一、


二、


三、


四、



五、


六、


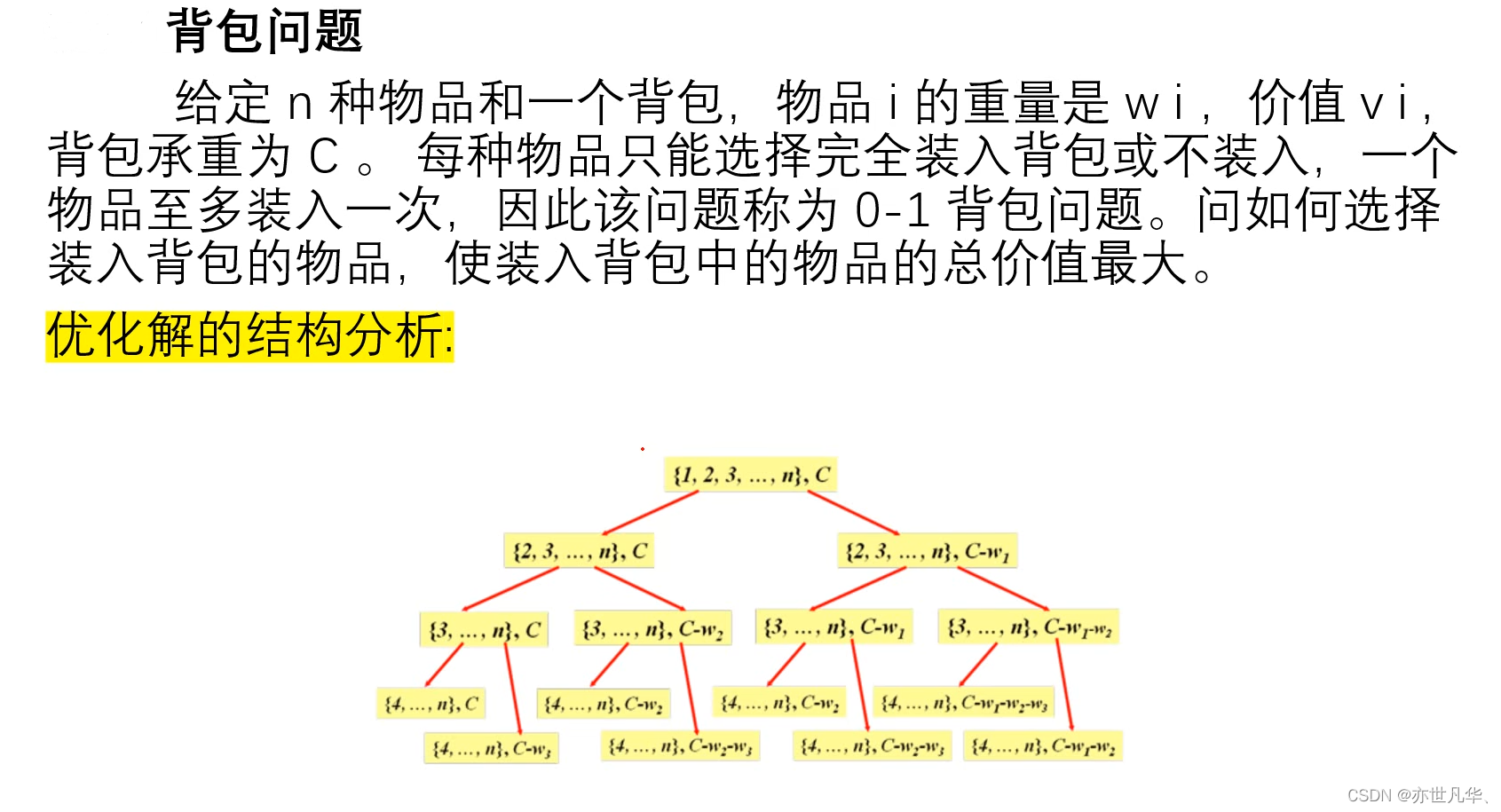
背包问题(0-1背包问题)


回溯法

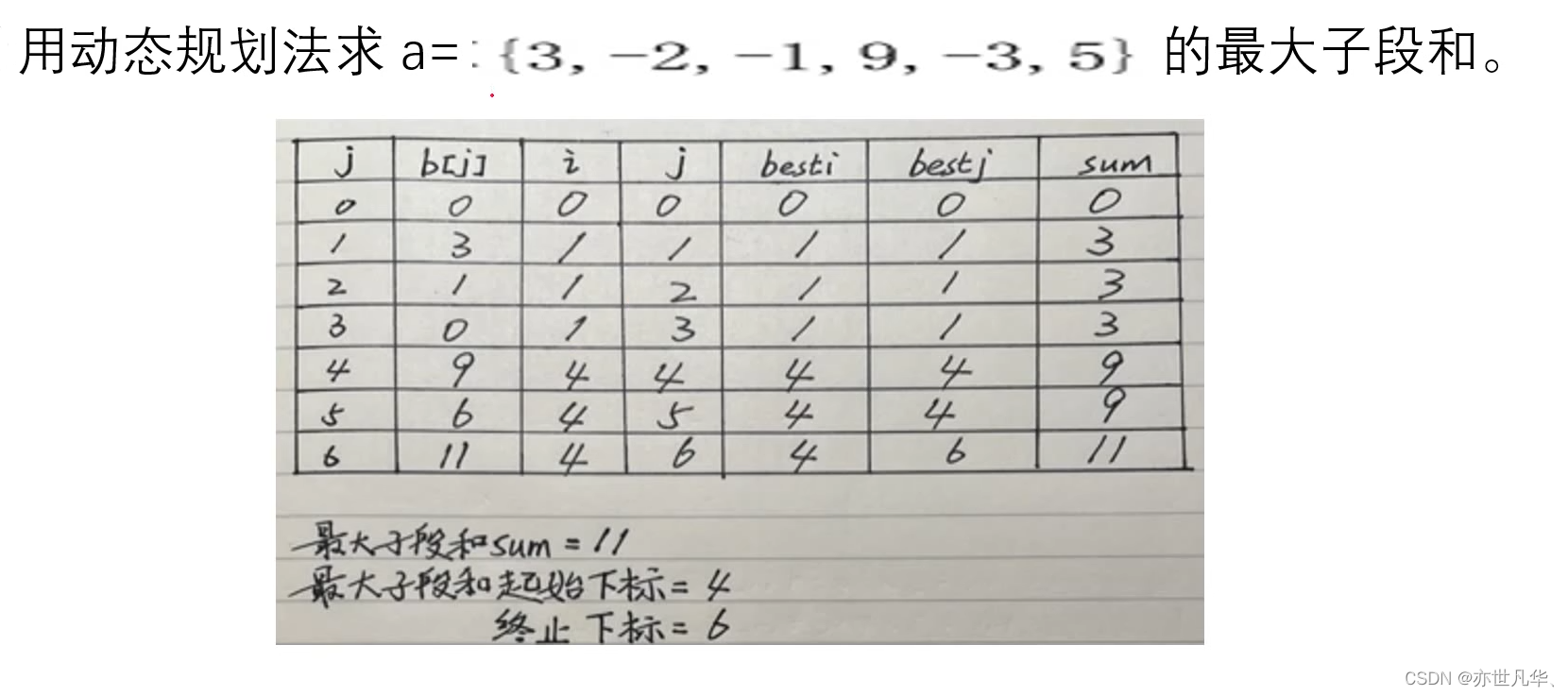
动态规划法



编程题
用回溯法解方程
#include<iostream>
using namespace std;int a[6] = { 0 };
int solution(int b[], int m, int n)
{if (m == n){if (b[0] * b[1] - b[2] * b[3] - b[4] == 1){printf("解为a=%d b=%d c=%d d=%d e=%d\n", b[0], b[1], b[2], b[3], b[4]);}return 0;}for (int i = 1; i <= n; i++){if (a[i] == 0){a[i] = 1;b[m] = i;solution(b, m + 1, n);a[i] = 0;}}
}
int main()
{int c[6];solution(c, 0, 5);return 0;
}
动态规划法解决蜘蛛吃蚊子
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cstdlib>int main(int argc, char** argv)
{int n = 5, i, j;if (argc == 2) n = std::stoi(argv[1]);std::vector<std::vector<int> > dp(n, std::vector<int>(n, 1));for (i = 1; i < n; ++i)for (j = 1; j < n; ++j){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}std::cout << "total path for " << n << "x" << n << " grid: " << dp[n - 1][n - 1] << std::endl;return 0;
}
用分治法解决抛硬币问题
#include <iostream>
#include <vector>
#include <string>
#include <cstdlib>
#include <numeric>
#include <time.h> int solve(std::vector<int>& a, int low, int high);int main(int argc, char** argv)
{int n = 100, m, ans;if (argc == 2) n = std::stoi(argv[1]);std::vector<int> a(n, 2);srand((unsigned)time(NULL));m = rand() % n; std::cout << "m: " << m << std::endl;a[m] = 1;std::cout << "solving ..." << std::endl;ans = solve(a, 0, n - 1);std::cout << "coin " << ans << " is fake" << std::endl;return 0;
}int solve(std::vector<int>& a, int low, int high)
{int sum1, sum2, mid, ret_val;if (low == high) return low; // 只有一个硬币if (low == high - 1) // 只有两个硬币{std::cout << " weighing coin " << low << " and " << high << std::endl;if (a[low] < a[high]) ret_val = low;else ret_val = high;std::cout << " --> coin " << ret_val << " is lighter" << std::endl;return ret_val;}mid = (low + high) / 2;if ((high - low + 1) % 2 == 0) // 硬币数量为偶数{sum1 = std::accumulate(a.begin() + low, a.begin() + mid + 1, 0);sum2 = std::accumulate(a.begin() + mid + 1, a.begin() + high + 1, 0);std::cout << " weighing coin " << low << "-" << mid << " and " << mid + 1 << "-" << high << std::endl;}else // 硬币数量为奇数{sum1 = std::accumulate(a.begin() + low, a.begin() + mid, 0);sum2 = std::accumulate(a.begin() + mid + 1, a.begin() + high + 1, 0);std::cout << " weighing coin " << low << "-" << mid - 1 << " and " << mid + 1 << "-" << high << std::endl;}std::cout << " sum1=" << sum1 << " , sum2=" << sum2 << std::endl;if (sum1 == sum2){std::cout << " --> equal" << std::endl;return mid;}else if (sum1 < sum2){std::cout << " --> the former is lighter" << std::endl;if ((high - low + 1) % 2 == 0) return solve(a, low, mid); // 偶数else return solve(a, low, mid - 1); // 奇数}else{std::cout << " --> the latter is lighter" << std::endl;return solve(a, mid + 1, high);}
}
用二分法分两边求最大值
#include<stdio.h>
void maxmin(int a, int b, int* min, int* max);
int array[9] = { 1,3,4,5,6,7,8,9,2 };int main() {int _max, _min;maxmin(0, 8, &_min, &_max);printf("MAX:%d, MIN:%d", _max, _min);
}void maxmin(int a, int b, int* min, int* max) {int lmax, lmin, rmax, rmin;if (a == b) *min = *max = array[a];else if (a == b - 1) {if (array[a] < array[b]) {*min = array[a];*max = array[b];}else {*min = array[b];*max = array[a];}}else {int mid = (a + b) / 2;maxmin(a, mid, &lmin, &lmax);maxmin(mid + 1, b, &rmin, &rmax);if (lmin < rmin) *min = lmin;else *min = rmin;if (rmax < lmax) *max = lmax;else *max = rmax;}}
相关文章:

【算法 | 例题简答】相关例题讲解
目录 简答题 计算题 时间复杂度的计算 递归算法计算 背包问题(0-1背包问题) 回溯法 动态规划法 编程题 用回溯法解方程 动态规划法解决蜘蛛吃蚊子 用分治法解决抛硬币问题 用二分法分两边求最大值 简答题 1、什么是算法?算法有哪…...
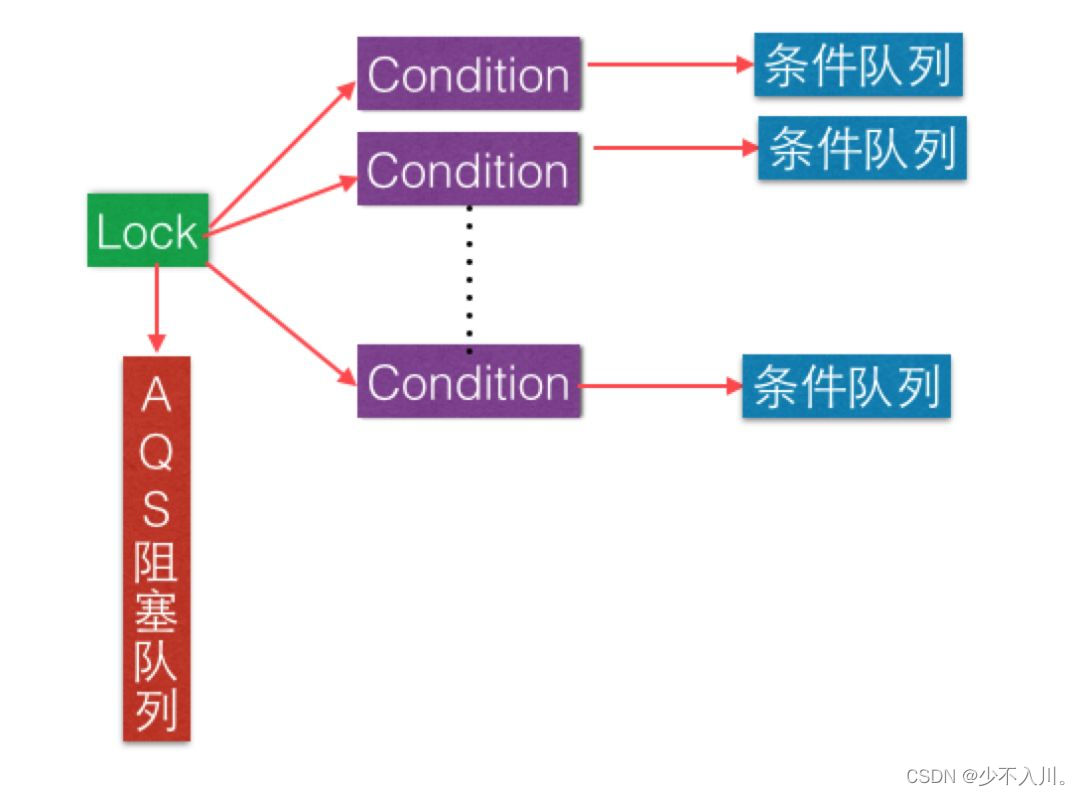
浅谈AQS
1.前言 AQS是AbstractQueuedSynchronizer(抽象同步队列)的简写,它是实现同步器的基础组件,并发包下的锁就是通过AQS实现的。作为开发者可能并不会直接用到AQS,但是知道其原理对于架构设计还是很有帮助的。 那为什么说…...

关于服务连接器(Servlet)你了解多少?
Servlet 1 简介 Servlet是JavaWeb最为核心的内容,它是Java提供的一门动态web资源开发技术。 使用Servlet就可以实现,根据不同的登录用户在页面上动态显示不同内容。 Servlet是JavaEE规范之一,其实就是一个接口,将来我们需要定义…...

面对学员的投诉,中创教育是如何处理的?
客户满意度的检测指标是客户的期望值和服务感知之间的差距。当顾客购买商品时,对商品本身和企业的服务都抱有良好的愿望和期盼值,如果这些愿望和要求得不到满足,就会失去心理平衡,由此产生的抱怨和想"讨个说法"的行为&a…...
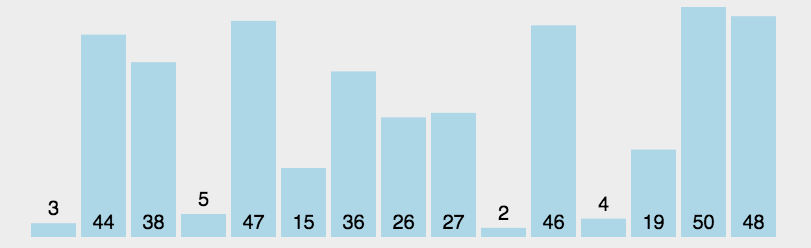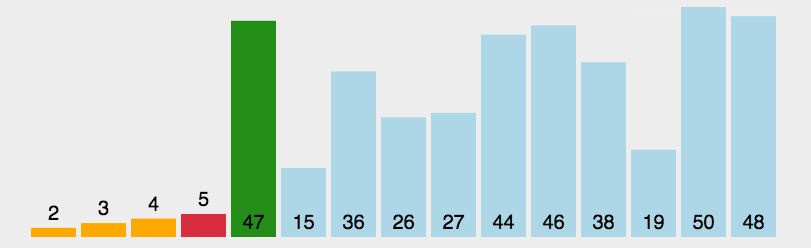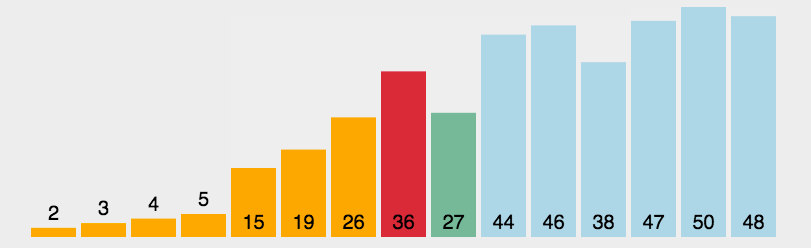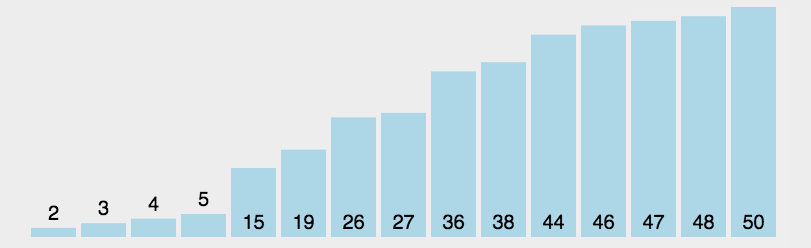
算法问题——排序算法问题
摘要 查找和排序算法是算法的入门知识,其经典思想可以用于很多算法当中。因为其实现代码较短,应用较常见。所以在面试中经常会问到排序算法及其相关的问题。但万变不离其宗,只要熟悉了思想,灵活运用也不是难事。一般在面试中最常…...

ArcGIS网络分析之构建网络分析数据集(一)
说明: 1. 本文主要用于演示网络分析服务的搭建过程。所以在此不会深入讨论网络分析服务的每一个细节,本文的目的就是让初学者学会使用网络分析服务进行基本的分析(主要针对后续的WEB开发):路径分析,最近设施点分析,以及服务区分析。 2.关于OD成本矩阵分析,多路径配送,…...

微电影的行业痛点有哪些?
微电影全称微型电影,又称微影。是指能够通过互联网新媒体平台传播(几分钟到60分钟不等)的影片,适合在移动状态、短时休闲状态下观看,具有完整故事情节的“微(超短)时”(几分钟-60分钟)放映、“微(超短)周期制作(7-15天…...
spark3.0源码分析-driver-executor心跳机制
前言 driver和executor心跳机制分为两种机制: 1、executor发送心跳机制 2、driver接受心跳机制 至于为何要分为两种,原因是在分布式场景中,服务的稳定性是无法保障的,例如executor宕机后无法发送心跳,故driver端需要…...
数据分析就要选择这款免费报表工具
对于一家企业来说,在日常运营的过程中本身就会产出很多的数据,那么这些数据本身就应该形成报表。可是如果只是选择手工的一种操作,确实需要浪费大量的人力物力。伴随着科技进入到快速发展的阶段,市面上更是出现了很多报表工具可以…...
node学习-3:服务器渲染和客户端渲染
1. 概念 一.服务端渲染,后端嵌套模板,后端渲染模板,SSR(后端把页面组装好) 做好静态页面,动态效果 把前端代码提供给后端,后端则把静态html以及里面的假数据给删除掉 通过模板进行动态生成h…...

LeetCode刷题笔记和周赛题解总目录
之前一段时间一直在刷LeetCode,在上面积累了很多笔记,这些笔记是做题过程中的一些重要积累和心得,现在将它们汇总和总结至此,此博客将不断更新。 刷题笔记(提供md和pdf两种格式可供下载,不断更新) LeetCode刷题笔记 …...

用类比方式学习编程中函数递归(个人理解仅供参考)(内含汉诺塔问题的求解)
目录 1.前言 2.递归的数学模型 3.相关的c语法 4.将递归的数学模型写成编程语言 5.利用类比方法将实际问题的代码写成函数递归的形式 例1: 例2: 6.汉诺塔问题的求解 1.前言 本人在学习函数递归编程方法的过程中,发现用类比的方式学习递归法可帮助我们在各种编…...

【云原生之Docker实战】使用Docker部署Taskover开源个人任务管理工具
【云原生之Docker实战】使用Docker部署Taskover 开源个人任务管理工具 一、Taskover介绍1.Taskover 简介2.Taskover功能二、检查本地docker环境1.检查系统版本2.检查docker版本3.检查docker状态4.检查docker compose版本三、下载Taskover镜像四、部署Taskover应用1.创建安装目录…...

5、SQL编程开发与注意事项
1.1 导入数据 导入测试库: 文档地址: https://dev.mysql.com/doc/employee/en/sakila-structure.html下载地址: https://github.com/datacharmer/test_db导入测试库: mysql -uroot -p -S < employees.sql 1.2 库操作 增:create database test character set utf8;删:d…...
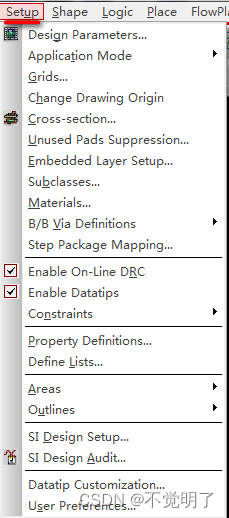
Allegro如何通过视图显示区分动态和静态铜皮操作指导
Allegro如何通过视图显示区分动态和静态铜皮操作指导 用Allegro做PCB设计的时候,通常动态和静态铜皮是无法通过视图显示区分的,只能通过show element查看得知,如下图 左边铜皮是动态铜皮,右边是静态铜皮 但Allegro可以通过一些设置让动静态铜皮以不同效果显示出来 具体操…...

测试开发之Django实战示例 第十一章 渲染和缓存课程内容
第十一章 渲染和缓存课程内容在上一章中,使用了模型继承和通用关系建立弹性的课程、章节和内容的关联数据模型,并且建立了一个CMS系统,在其中使用了CBV,表单集和AJAX管理课程内容。在这一章将要做的事情是:创建公开对外…...
90%企业在探索的敏捷开发怎么做?极狐GitLab总结了这些逻辑与流程
本文来自: 彭亮 极狐(GitLab) 高级产品经理 毛超 极狐(GitLab) 研发工程师 极狐(GitLab) 市场部内容团队 “敏捷” 是指能够驾驭变化,保持组织竞争优势的一种能力。自 2001 年《敏捷宣言》以来,敏捷及敏捷开发理念逐渐席卷全球。中国信通院《…...

LeetCode-257. 二叉树的所有路径
目录题目分析递归法题目来源 257. 二叉树的所有路径 题目分析 前序遍历以及回溯的过程如图: 递归法 1.递归函数参数以及返回值 要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值,代…...

测试用例该怎么设计?—— 日常加更篇(下)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...

Java基础:接口
1.接口的概念 当不是所有子类, 而是多个子类都包含一个方法时, 为了代码书写规范性, 可以用自定义的接口来统一该方法的书写规范. 所以接口可以看作是一种书写规则. 接口是对行为的抽象 抽象类一般是书写在父类当中, 接口是单独书写的, 不是一种类 2.接口的定义和使用 3.接口…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
