「SDOI2009」HH去散步
HH去散步
题目限制
- 内存限制:125.00MB
- 时间限制:1.00s
- 标准输入
- 标准输出
题目知识点
- 动态规划 dpdpdp
- 矩阵
- 矩阵乘法
- 矩阵加速
- 矩阵快速幂
- 思维
- 构造
题目来源
「SDOI2009」HH去散步
题目
题目背景
HH 有个一成不变的习惯,喜欢在饭后散步,就是在一定的时间内,走一定的距离
同时, HH 是一个喜欢变化的人,她不会立刻沿着刚刚走过来的路走回去,她也希望每天走过的路径都不完全一样,她想知道每一天他究竟有多少种散步的方法
题目描述
现在 HH 送给你一张学校的地图,请你帮助她求出从地点 AAA 走到地点 BBB 一共有多少条长度为 TTT 的散步路径(答案对 459894598945989 取模)
格式
输入格式
输入共 M+1M + 1M+1 行:
第 111 行:输入 555 个整数 N,M,T,A,BN, \ M, \ T, \ A, \ BN, M, T, A, B;NNN 表示 学校里的路口的个数(编号为 0∼N−10 \sim N - 10∼N−1),MMM 表示 学校里的道路的条数,TTT 表示 HH 想要散步的距离,AAA 表示 散步的出发点, BBB 表示 散步的终点
接下来 MMM 行:每行 222 个用空格隔开的整数 ui,viu_i, \ v_iui, vi;表示 长度为 111 的第 iii 条路 连接 路口 uiu_iui 和 路口 viv_ivi
输出格式
输出共一行:表示你所求出的答案(对 459894598945989 取模)
样例
样例输入
4 5 3 0 0
0 1
0 2
0 3
2 1
3 2
样例输出
4
提示
数据范围
对于 30%30 \%30% 的数据:满足 N≤4,M≤10,T≤10N \leq 4, \ M \leq 10, \ T \leq 10N≤4, M≤10, T≤10
对于 100%100 \%100% 的数据:满足 N≤50,M≤60,T≤230,ui≠viN \leq 50, \ M \leq 60, \ T \leq 2 ^ {30}, \ u_i \neq v_iN≤50, M≤60, T≤230, ui=vi
思路
这道题如果没有 她不会立刻沿着刚刚走过来的路走回去 的限制,就可以根据点与点的关系先构造出一个 n∗nn * nn∗n 的矩阵 x\mathrm{x}x(x[i][j]\mathrm{x}[i][j]x[i][j] 表示从 iii 走 111 步到 jjj 的方案数),累乘 TTT 次(就是走了 TTT 步),就用矩阵快速幂优化既可以通过了
现在就考虑加上这句话的限制后如何构造矩阵了
分析
考虑矩阵定义大致不变,即 x[i][j]\mathrm{x}[i][j]x[i][j] 表示从 iii 走 111 步到 jjj 的方案数
由于有限制,就要记录刚刚走过来的路是哪一条
不妨把每条边对应的 uiu_iui 和 viv_ivi 拆成两个二元组 (node,id)\mathrm{(node, id)}(node,id),表示刚刚从第 id\mathrm{id}id 条路走到 node\mathrm{node}node,也就是每条无向边 (ui↔,vi)(u_i \leftrightarrow, v_i)(ui↔,vi) 分成两条有向边 (ui→vi)(u_i \to v_i)(ui→vi) 和 (vi→ui)(v_i \to u_i)(vi→ui),其中 node\mathrm{node}node 表示当前这条有向边的终点,id\mathrm{id}id 表示与之对应的无向边的编号
那么 x[i][j]=1\mathrm{x}[i][j] = 1x[i][j]=1 定义就是 第 iii 个二元组 走 111 步到 第 jjj 个二元组 的方案数
其值只可能为 000 或 111(因为只走了 111 步),其中值为 111 的条件就是 idi≠idj\mathrm{id}_i \neq \mathrm{id}_jidi=idj 且 nodei\mathrm{node}_inodei 与 nodej\mathrm{node}_jnodej 有一条边
推出了矩阵,但是还有一个细节,就是第一步的方案数
起始点是没有上一条边的,所以需要预处理一下(这里相当于先走了一次)
预处理矩阵 ×\times× 矩阵快速幂(T−1T - 1T−1 次,预处理走了一次)就可以得到最终的矩阵了
最后把 起始点(超级源点) 到 终点(可能有多个,因为分了边) 的路径加起来取模就可以了
代码
#include <cstdio>
#include <cstring>int rint()
{int x = 0, fx = 1; char c = getchar();while (c < '0' || c > '9') { fx ^= ((c == '-') ? 1 : 0); c = getchar(); }while ('0' <= c && c <= '9') { x = (x << 3) + (x << 1) + (c ^ 48); c = getchar(); }if (!fx) return -x;return x;
}const int MOD = 45989;const int MAX_N = 20;
const int MAX_M = 60;int N, M, T, A, B, node;
int e[MAX_M * 2 + 5][3];struct Matrix
{int mx[MAX_M * 2 + 5][MAX_M * 2 + 5];Matrix () { memset(mx, 0, sizeof(mx)); }void init() { for (int i = 0; i <= node; i++) mx[i][i] = 1; }Matrix operator * (const Matrix &rhs) const{Matrix res;for (int i = 0; i <= node; i++)for (int j = 0; j <= node; j++)for (int k = 0; k <= node; k++)res.mx[i][j] = (res.mx[i][j] + mx[i][k] * rhs.mx[k][j]) % MOD;return res;}
} dp, quick;Matrix qpow(Matrix mx, int k)
{Matrix res; res.init();while (k > 0){if (k & 1) res = res * mx;mx = mx * mx; k >>= 1;}return res;
}int main()
{N = rint(), M = rint(), T = rint();A = rint() + 1, B = rint() + 1;for (int i = 1; i <= M; i++){e[i][0] = rint() + 1, e[i][1] = rint() + 1;e[i + M][0] = e[i][1], e[i + M][1] = e[i][0];if (e[i][0] == A) ++dp.mx[0][i];if (e[i + M][0] == A) ++dp.mx[0][i + M];}node = M << 1;for (int i = 1; i <= node; i++)for (int j = 1; j <= node; j++)if (i + M != j && i - M != j && e[i][1] == e[j][0]) ++quick.mx[i][j];int ans = 0;Matrix res = dp * qpow(quick, T - 1);for (int i = 1; i <= node; i++)if (e[i][1] == B) ans = (ans + res.mx[0][i]) % MOD;printf("%d\n", ans);return 0;
}相关文章:

「SDOI2009」HH去散步
HH去散步 题目限制 内存限制:125.00MB时间限制:1.00s标准输入标准输出 题目知识点 动态规划 dpdpdp矩阵 矩阵乘法矩阵加速矩阵快速幂 思维 构造 题目来源 「SDOI2009」HH去散步 题目 题目背景 HH 有个一成不变的习惯,喜欢在饭后散步…...

用上Visual Studio后,我的世界游戏的构建时间减少了一半
今天我们讲述一个使用 Visual Studio 提升工作效率的案例。 我的世界(Minecraft) 游戏开发商 Mojang Studios 近日联系了 Visual Studio C 团队,因为他们需要将 C 开发扩展到新平台(Linux),同时还希望保留他们现有的技术基础&…...
34、基于51单片机锂电池电压电流容量检测仪表LCD液晶显示 原理图PCB程序设计
方案选择 单片机的选择 方案一:AT89C52是美国ATMEL公司生产的低电压,高性能CMOS型8位单片机,器件采用ATMEL公司的高密度、非易失性存储技术生产,兼容标准MCS-51指令系统,片内置通用8位中央处理器(CPU)和Flash存储单元…...
-基础使用)
【Java基础】泛型(一)-基础使用
本文以Java的官方文档为参考,辅以代码示例,尽可能详尽的叙述泛型的每一个特性 什么是泛型 泛型(Generics)也称为参数化类型(parameterized types),也就是将类型本身作为接口、类、方法中的参数…...

学Python不会不知道NumPy计算包吧,带你五分钟看懂NumPy计算包
从今天我们就开始进入 Python 数据分析工具的教程。 前段时间数据分析和Python都讲了一点点,但是Python的数据库,讲的少了点,所以接下来就讲讲这些重要的常用数据库吧!!! Python 数据分析绝对绕不过的四个…...
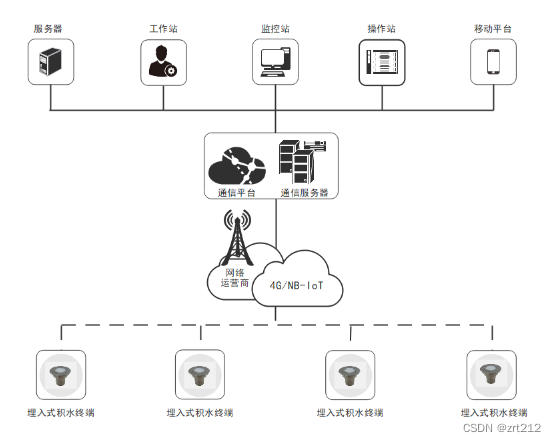
积水内涝监测——埋入式积水终端设备介绍
一、设备概述 埋入式积水终端是针对城市内涝推出的积水信息监测采集设备,采用超声波传感技术,对积水的深度进行精确的测量。产品能够在低温、腐蚀环境下可靠运行本产品特别适用于智慧城市中,对城市道路、社区低洼处的积水进行实时监测上报到…...
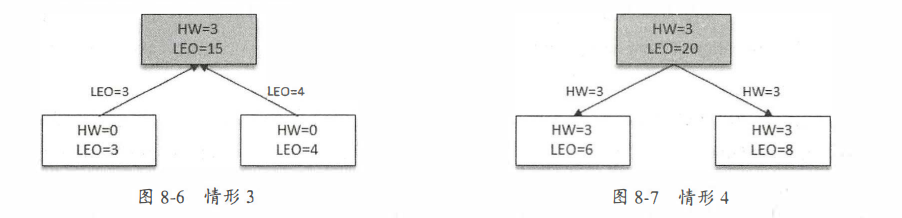
Kafka的日志同步
首先介绍下LEO和HW LEO: 即LogEndOffset,表示该副本下次日志记录的偏移量HW:即HighWatermark,高水位线,是所有ISR副本集合中的LEO最小值上图中,如果此时三个副本都在ISR集合中,那么此时他们的LE…...
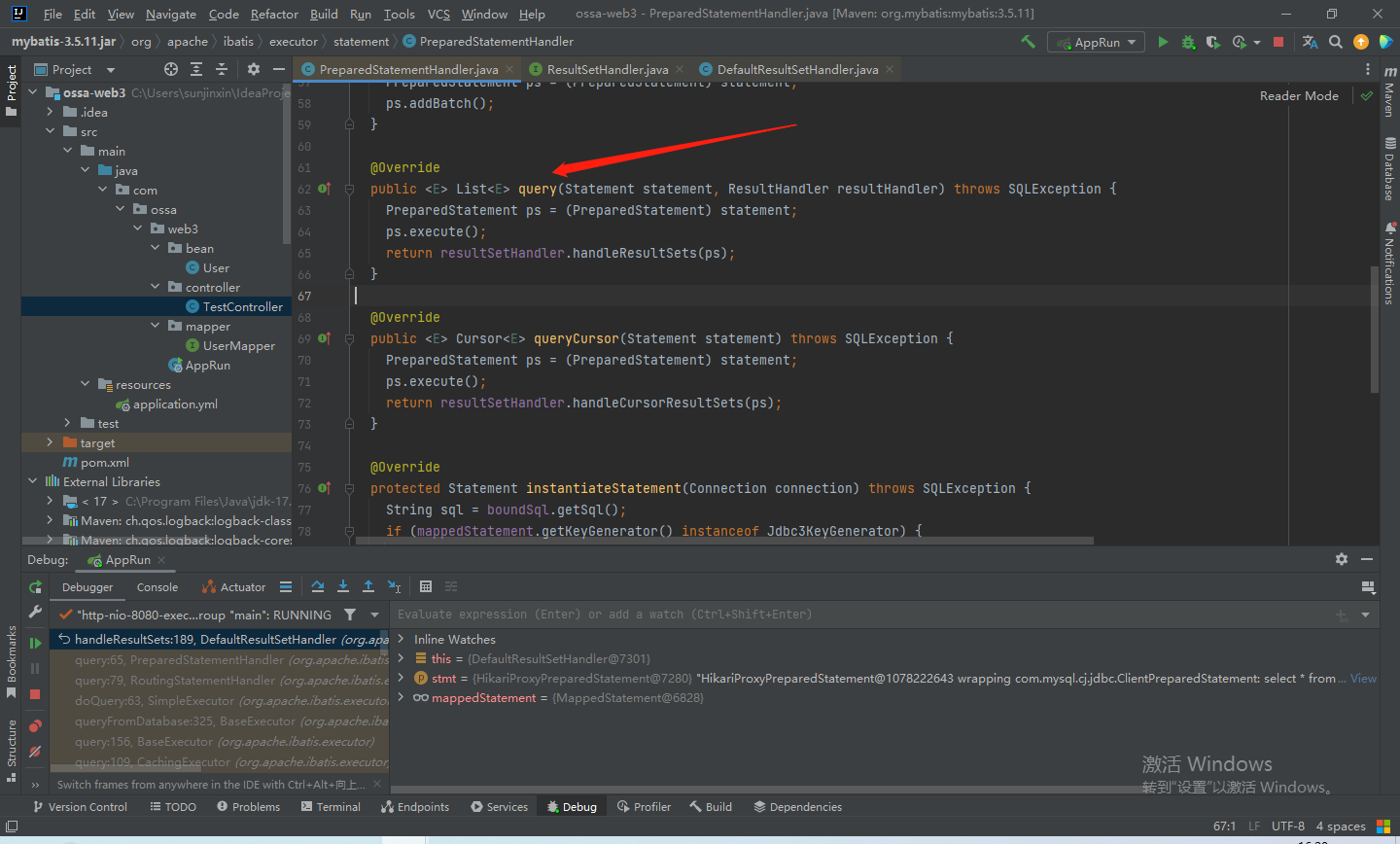
【Mybatis源码解析】mapper实例化及执行流程源码分析
文章目录简介环境搭建源码解析基础环境:JDK17、SpringBoot3.0、mysql5.7 储备知识:《【Spring6源码・AOP】AOP源码解析》、《JDBC详细全解》 简介 基于SpringBoot的Mybatis源码解析: 1.如何对mapper实例化bean 在加载BeanDefinition时&a…...
分布式文件管理系统(MinIO)
1.去中心化,每个点是对等的关系,通过Ngix对负载做均衡工作。 好处: 能够避免单点故障,将多块硬盘组成一个对象存储服务。 2. 使用纠删编码技术来保护数据,是一种回复丢失和损坏的数据的数学算法,他将数据分…...

Springcloud-配置中心config
一、添加依赖<dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-config-server</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId&…...

[项目篇] 音乐播放器开发报告
文章目录1. 项目描述:2. 项目上线展现:3. 项目具体实现:1. 登录2. 注册3.退出系统4.添加音乐4.1前后端交互约定4.2上传文件业务逻辑:4.3创建model包中的music类4.4在MusicMapper接口中,声明insertMusic抽象方法4.5在mybatis包中添…...
Spring Cloud Alibaba--gateway微服务详解之网关(二)
1、网关介绍 上篇对微服务中的nacos注册中心进行集成讲解。nacos主要作用是管理多服务之间复杂关系的组件。微服务是非常庞大且问题突出的架构,HTTP协议具有跨源资源共享 (CORS) Cross- Origin Resource Sharing机制,而处于安全考虑往往前端架构都会对跨…...
Zynq非VDMA方案实现视频3帧缓存输出,无需SDK配置,提供工程源码和技术支持
目录1、前言2、VDMA的不便之处3、FDMA取代VDMA实现视频缓存输出4、Vivado工程详解5、上板调试验证并演示6、福利:工程代码的获取1、前言 对于Zynq和Microblaze的用户而言,要想实现图像缓存输出,多半要使用Xilinx推荐的VDMA方案,该…...

血液透析过滤芯气密性检测装置中的高精度多段压力控制解决方案
摘要:针对目前血液过滤芯气密性检测过程中存在的自动化水平较低、多个检测压力之间需人工切换和压力控制精度较差的问题,为满足客户对高精度和自动化气密性检测的要求,本文提出了相应的解决方案。解决方案的主要特点是全过程的可编程压力控制…...
PDF加密如何批量解除?快来了解下这个方法
在现代办公环境中,PDF文档的使用非常普遍。然而,由于一些安全需求,有时候PDF文档会被加密,使得只有授权人员可以查看或修改它。但是,如果您需要对许多加密PDF文档进行操作,逐个解密这些文档可能非常费时费力…...

C++——哈希4|布隆过滤器
目录 布隆过滤器 完整代码 布隆过滤器应用 布隆过滤器的查找 布隆过滤器删除 布隆过滤器优点 布隆过滤器缺陷 布隆过滤器海量数据处理 布隆过滤器 位图只能映射整形,而对于字符串却无能为力。 把字符串用哈希算法转成整形,映射一个位置进行标…...
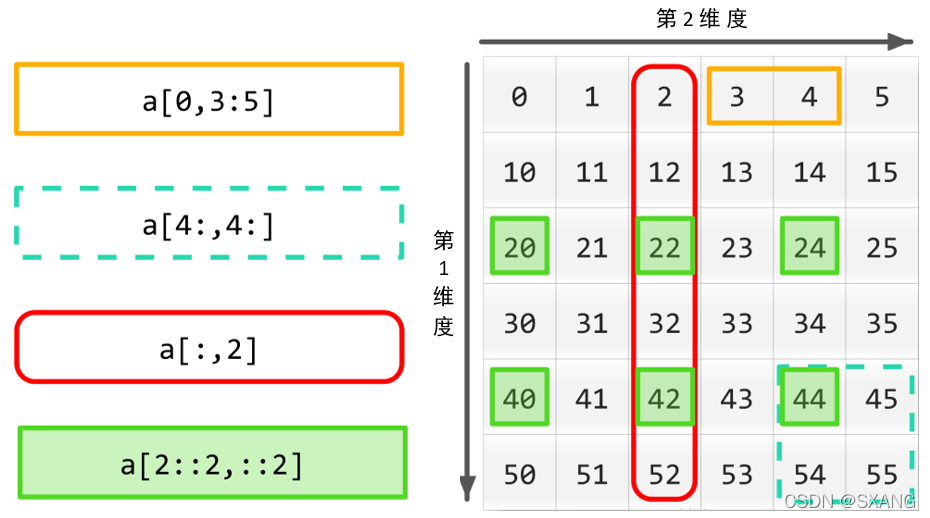
python冒号的用法总结
一维数组 1. 单个冒号的情况 1.1 写完整的情况下 单个冒号的情况下,对数组的遍历操作是从前向后操作。如:arr[a:b] ,冒号前的a含义是从a开始遍历,冒号后的b含义是到b截止(不包括b)。 arr [1, 2, 3, 4,…...

面试题整理
面试题整理 一、Java基础 1、Java 语言有哪些特点 简单易学; 面向对象(封装,继承,多态); 平台无关性( Java 虚拟机实现平台无关性); 支持多线程( C 语言…...
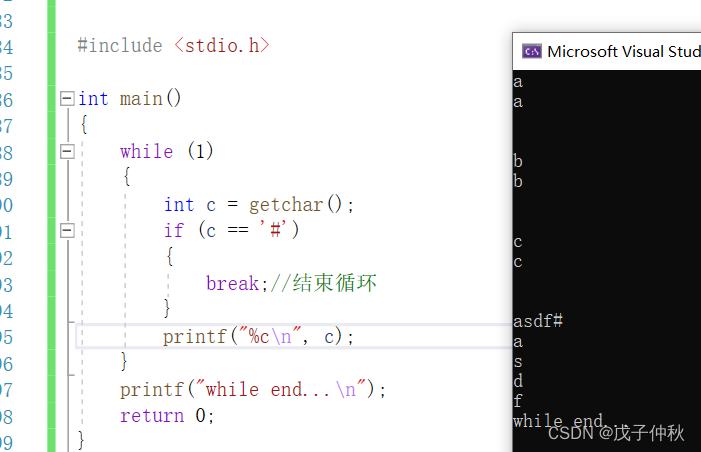
C语言深度解剖-关键字(7)
目录 switch case 语句 理解: 补充: 深入理解: default 语句: case语句: 总结: do、while、for 关键字 while for do while 各种死循环方法: while for do while getchar 写在…...

利用JavaScript编写Python内置函数查询工具
最近我开始学习Python编程语言,我发现Python拥有非常丰富的内置函数,可以用来实现各种不同的功能。但是每当我需要查找一个内置函数时,我总是需要联网使用搜索引擎进行查询。这种方式不仅费时费力,而且需要联网,很不方…...

LeetCode 3296.移山所需的最少秒数:优先队列
【LetMeFly】3296.移山所需的最少秒数:优先队列 力扣题目链接:https://leetcode.cn/problems/minimum-number-of-seconds-to-make-mountain-height-zero/ 给你一个整数 mountainHeight 表示山的高度。 同时给你一个整数数组 workerTimes,表…...

从局部对比度到注意力机制:ALCNet如何革新红外小目标检测
1. 红外小目标检测:一个“大海捞针”的经典难题 大家好,我是老张,在AI和计算机视觉领域摸爬滚打了十几年,尤其对红外图像处理这块儿情有独钟。今天想和大家深入聊聊一个听起来就挺“硬核”的话题——红外小目标检测。你可能觉得这…...

深耕智慧供热 铸就行业口碑|河北唐仪室温采集器市场地位与实力解析
随着智慧供热全面升级、供暖精细化管理成为行业发展主流,室温采集器作为热源调控、能耗优化、用户服务的核心终端设备,市场需求持续增长。河北唐仪自控设备有限公司深耕供热自动化领域多年,专注室温采集设备研发、生产与系统集成,…...

Maxwell Optislang的谐响应与多物理场计算在永磁电机多目标优化参数化建模及电磁振...
maxwell ,optislang 谐响应,,多物理场计算永磁电机多目标优化参数化建模电磁振动噪声仿真永磁电机的多物理场优化就像在玩一场精密的多维拼图游戏。当电磁性能、振动噪声和热特性这几个看似矛盾的指标需要同时满足时,传统单学科优…...

电商品牌数字化获客工具排行榜适配精准需求
电商品牌数字化获客工具排行榜适配精准需求一、行业背景与排行依据据《2026中小企业数字化获客白皮书》数据显示,当前国内83%的电商品牌面临获客成本攀升、用户精准度不足的问题,人工运营效率仅为自动化工具的17%,数字化获客已成为企业增长的…...

Flutter 三方库 rabbit_converter 的鸿蒙化适配指南 - 让消息转换回归“工业化标准”,打造鸿蒙应用专家级的 RabbitMQ 数据适配中台
欢迎加入开源鸿蒙跨平台社区:https://openharmonycrossplatform.csdn.net Flutter 三方库 rabbit_converter 的鸿蒙化适配指南 - 让消息转换回归“工业化标准”,打造鸿蒙应用专家级的 RabbitMQ 数据适配中台 前言 在鸿蒙(OpenHarmony&…...

【MoveIt 2】利用MoveIt任务构造器实现多阶段物体抓取与放置任务
1. 为什么需要MoveIt任务构造器?从“硬编码”到“乐高式”编程 如果你曾经尝试用MoveIt 2的MoveGroupInterface来写一个完整的“抓取-移动-放置”任务,我猜你大概率会经历一段“痛苦”的时光。我刚开始做机械臂应用的时候,也是这么过来的&…...

IPED内存取证流程:从内存镜像到证据报告的完整指南
IPED内存取证流程:从内存镜像到证据报告的完整指南 【免费下载链接】IPED IPED Digital Forensic Tool. It is an open source software that can be used to process and analyze digital evidence, often seized at crime scenes by law enforcement or in a corp…...

揭秘tidytext核心功能:unnest_tokens如何实现文本数据的一键整洁化
揭秘tidytext核心功能:unnest_tokens如何实现文本数据的一键整洁化 【免费下载链接】tidytext Text mining using tidy tools :sparkles::page_facing_up::sparkles: 项目地址: https://gitcode.com/gh_mirrors/ti/tidytext tidytext是一款基于整洁工具的文本…...

Oh My Zsh 使用指南:Zsh 终端配置与插件管理教程
carbon在 Linux 或 macOS 系统中,终端是开发者和运维人员每天都会使用的重要工具。 默认的 Bash 终端虽然功能完整,但在使用体验和效率方面还有很大的提升空间。 例如: 命令自动补全 终端主题美化 插件扩展 Git 快捷命令 因此很多开发者会…...
