【算法】单调栈问题
文章目录
- 题目
- 思路分析
- 代码实现
题目
给定一个不含有重复值的数组arr,找到每一个i位置左边和右边离i位置最近且值比arr[i]小的位置,返回所有位置相应的消息。
比如arr={3,4,1,5,6,2,7},返回如下二位数组作为结果:{[-1, 2], [0, 2], [-1, -1], [2, 5], [3, 5], [2, -1], [5, -1]}
-1表示不存在,比如arr中,0位置的左边没有元素,所以是-1.右边最小的是1这个数据位置,也就是index=2,所以得到{-1,2}。
如果我给定是一个可能含有重复值的数组arr呢?
要求时间复杂度为O(N)。
思路分析
如果是时间复杂度为O(N2)的,那么我们直接暴力解决即可,都是如果这样子做,这道题肯定就g了。
我们先来分析无重复的数组的情况。
原问题:
准备一个栈,记为 Stack<Integer>,栈中放的元素是数组的位置,开始时stack 为空。如果找到每一个i位置左边和右边离i位置最近且值比 arrli]小的位置,那么需要让stack 从栈顶到栈底的位置所代表的值是严格递减的;如果找到每一个i位置左边和右边离i位置最近且值比 arr[i]大的位置,那么需要让 stack 从栈顶到栈底的位置所代表的值是严格递增的。
本题需要解决的是前者,但是对于后者,原理完全是一样的。
下面用例子来展示单调栈的使用和求解流程,初始时 arr = {3,4,1,5,6,2,7},stack 从栈顶到栈底为:{}
遍历到arr[0]==3,发现stack为空,就直接放入0位置。stack 从栈顶到栈底为:{0位置(值是3));
遍历到arr[1]==4,发现直接放入1位置,不会破坏stack 从栈顶到栈底的位置所代表的值是严格递减的,那么直接放入。stack从栈顶到栈底依次为:(1位置(值是4)、0位置(值是3);
遍历到arr[2]==1,发现直接放入2位置(值是1),会破坏stack 从栈顶到栈底的位置所代表的值是严格递减的,所以从 stack开始弹出位置。如果x位置被弹出,在栈中位于x位置下面的位置,就是x位置左边离x位置最近且值比 arr[x]小的位置;
当前遍历到的位置就是x位置右边离x位置最近且值比 arr[x]小的位置。
从 stack弹出位置1,在栈中位于1位置下面的是位置0,当前遍历到的是位置2,所以 ans[1]=(0.2}。
弹出1位置之后,发现放入2位置(值是1)还会破坏stack 从栈顶到栈底的位置所代表的值是严格递减的,所以继续弹出位置0。
在栈中位于位置0下面已经没有位置了,说明在位置О左边不存在比 arr[0]小的值,当前遍历到的是位置2,所以ans[0]=(-1,2}。stack 已经为空,所以放入2位置(值是1),stack从栈顶到栈底为:{2位置(值是1));
遍历到 arr[3]==5,发现直接放入3位置,不会破坏stack 从栈顶到栈底的位置所代表的值是严格递减的,那么直接放入。stack 从栈顶到栈底依次为:3位置(值是5)、2位置(值是1);
遍历到 arr[4]==6,发现直接放入4位置,不会破坏 stack 从栈顶到栈底的位置所代表的值是严格递减的,那么直接放入。stack从
栈顶到栈底依次为:{(4位置(值是6)、3位置(值是5)、2位置(值是1);
遍历到 arr[5]==2,发现直接放入5位置,会破坏stack从栈顶到栈底的位置所代表的值是严格递减的,所以开始弹出位置。弹出位置4,栈中它的下面是位置3,当前是位置5, ans[4]=(3,5}。弹出位置3,栈中它的下面是位置2,当前是位置5,ans[3]=(2,5}。然后放入5位置就不会破坏stack的单调性了。stack从栈顶到栈底依次为:{5位置(值是2)、2位置(值是1)};
遍历到arr[6]==7,发现直接放入6位置,不会破坏stack从栈顶到栈底的位置所代表的值是严格递减的,那么直接放入。stack从栈顶到栈底依次为:{6位置(值是7)、5位置(值是2)、2位置(值是1)}。
遍历阶段结束后,清算栈中剩下的位置。
弹出6位置,栈中它的下面是位置5,6位置是清算阶段弹出的,所以 ans[6]={5,-1];弹出5位置,栈中它的下面是位置2,5位置是清算阶段弹出的,所以 ans[5]={2,-1];弹出2位置,栈中它的下面没有位置了,2位置是清算阶段弹出的,所以 ans[2]=(-1,-1]。
至此,已经全部生成了每个位置的信息。
我们可以按照上面的流程写出如下的代码
public static int[][] monotonicStackNorepeat(int[] arr) {Stack<Integer> stack = new Stack<>();int[][] res = new int[arr.length][2];for (int i = 0; i < arr.length; i++) {//如果当前栈不为空并且当前值比栈顶对应的元素小//那么就开始出栈 因为这说明栈内元素遇到了比自己小的数据了//并且一直出栈直到栈顶元素比当前元素小while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {//出栈得到栈顶元素对应的索引int popIndex = stack.pop();//判断栈顶元素的左边是否还有元素 如果有 那么比栈顶元素的左边最小就是这个元素int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();res[popIndex][0] = leftLessIndex;//比栈顶元素右边小的元素的位置为ires[popIndex][1] = i;}//放入当前元素 开启新一轮循环stack.push(i);}//清算阶段 对于还在栈中的元素while (!stack.isEmpty()) {//取出当前元素对应的索引位置int popIndex = stack.pop();//判断是否他们的左边还有值?左边的值都是比他们小的值int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();res[popIndex][0] = leftLessIndex;//清算阶段还在栈中说明他们的右边都是比他们大的或者就是已经没有后面的元素了res[popIndex][1] = -1;}return res;}
对于进阶问题,她的情况是,可能出现重复的数据,但是大体的解答流程差不多,思路如下:
进阶问题,可能含有重复值的数组如何使用单调栈。其实整个过程和原问题的解法差不多。举个例子来说明,初始时 arr={3,1,3,4,3,5,3,2,2],stack从栈顶到栈底为:{};
遍历到 arr[0]==3,发现stack为空,就直接放入0位置。stack 从栈顶到栈底为:{0位置(值是3)};
遍历到arr[1]==1,从栈中弹出位置0,并且得到ans[0]=[-1,1}。位置1进栈,stack从栈顶到栈底为:{1位置(值是1)};
遍历到arr[2]==3,发现位置2可以直接放入。stack从栈顶到栈底依次为:{2位置(值是3).1位置(值是1)};
遍历到 arr[3]==4,发现位置3可以直接放入。stack从栈顶到栈底依次为:{3位置(值是4)、2位置(值是3)、1位置(值是1)};
遍历到arr[4]==3,从栈中弹出位置3,并且得到ans[3]={2,4}。此时发现栈顶是位置2,值是3,当前遍历到位置4,值也是3,所以两个位置压在一起。stack 从栈顶到栈底依次为:{2位置,4位置、1位置(值是1)};
遍历到arr[5]==5,发现位置5可以直接放入。stack 从栈顶到栈底依次为:{5位置(值是5)、2位置,4位置、1位置(值是1));
遍历到arr[6]==3,从栈中弹出位置5,在栈中位置5的下面是[2位置,4位置],选最晚加入的4位置,当前遍历到位置6,所以得到 ans[5]={4,6}。位置6进栈,发现又是和栈顶位置代表的值相等的情况,所以继续压在一起,stack 从栈顶到栈底依次为:{2位置,4位置,6位置、1位置(值是1)};
遍历到arr[7]==2,从栈中弹出[2位置,4位置,6位置],在栈中这些位置下面的是1位置,当前是7位置,所以得到ans[2]=(1,7]、ans[4]=(1,7]、ans[6]={1,7}]。位置7进栈,stack 从栈顶到栈底依次为:{7位置(值是2)、1位置(值是1)};
遍历到arr[8]==2,发现位置8可以直接进栈,并且又是相等的情况,stack从栈顶到栈底依次为:{7位置,8位置、1位置(值是1)}。
遍历完成后,开始清算阶段:
弹出[7位置,8位置],生成ans[7]={1,-1]、ans[8]={1,-1};弹出1位置,生成ans[1]={-1,-1}。
完整代码贴在下面:
代码实现
package com.base.learn.stack;import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;/*** @author: 张锦标* @date: 2023/5/28 11:00* MonotonicStack类* 单调栈题目*/
public class MonotonicStack {public static int[][] violentSolution(int[] arr) {int[][] res = new int[arr.length][2];for (int i = 0; i < arr.length; i++) {int leftMin = -1;int rightMin = -1;int cur = i - 1;while (cur >= 0) {if (arr[cur] < arr[i]) {leftMin = cur;break;}cur--;}cur = i + 1;while (cur < arr.length) {if (arr[cur] < arr[i]) {rightMin = cur;break;}cur++;}res[i][0] = leftMin;res[i][1] = rightMin;}return res;}public static int[][] monotonicStackNorepeat(int[] arr) {Stack<Integer> stack = new Stack<>();int[][] res = new int[arr.length][2];for (int i = 0; i < arr.length; i++) {//如果当前栈不为空并且当前值比栈顶对应的元素小//那么就开始出栈 因为这说明栈内元素遇到了比自己小的数据了//并且一直出栈直到栈顶元素比当前元素小while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {//出栈得到栈顶元素对应的索引int popIndex = stack.pop();//判断栈顶元素的左边是否还有元素 如果有 那么比栈顶元素的左边最小就是这个元素int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();res[popIndex][0] = leftLessIndex;//比栈顶元素右边小的元素的位置为ires[popIndex][1] = i;}//放入当前元素 开启新一轮循环stack.push(i);}//清算阶段 对于还在栈中的元素while (!stack.isEmpty()) {//取出当前元素对应的索引位置int popIndex = stack.pop();//判断是否他们的左边还有值?左边的值都是比他们小的值int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();res[popIndex][0] = leftLessIndex;//清算阶段还在栈中说明他们的右边都是比他们大的或者就是已经没有后面的元素了res[popIndex][1] = -1;}return res;}public static int[][] monotonicStackRepeat(int[] arr) {Stack<List<Integer>> stack = new Stack<>();int[][] res = new int[arr.length][2];for (int i = 0; i < arr.length; i++) {//如果当前栈不为空并且当前值比栈顶对应的元素小//那么就开始出栈 因为这说明栈内元素遇到了比自己小的数据了//并且一直出栈直到栈顶元素比当前元素小while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {//出栈得到栈顶元素对应的索引List<Integer> popList = stack.pop();//判断栈顶元素的左边是否还有元素 如果有 那么比栈顶元素的左边最小就是这个元素int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size()-1);for (Integer popi : popList) {res[popi][0]=leftLessIndex;res[popi][1] = i;}}//判断当前栈是否为空 不为空则取出栈顶列表并且放入当前元素if (!stack.isEmpty() && arr[stack.peek().get(0)]==arr[i]){stack.peek().add(Integer.valueOf(i));}else{//栈为空 或者当前元素与栈顶元素不一样 那么直接创建一个新的listArrayList<Integer> list = new ArrayList<>();list.add(i);stack.push(list);}}//清算阶段 对于还在栈中的元素while (!stack.isEmpty()) {//出栈得到栈顶元素对应的索引List<Integer> popList = stack.pop();//判断栈顶元素的左边是否还有元素 如果有 那么比栈顶元素的左边最小就是这个元素int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size()-1);for (Integer popi : popList) {res[popi][0]=leftLessIndex;res[popi][1] = -1;}}return res;}public static void main(String[] args) {System.out.println(Arrays.deepToString(monotonicStackNorepeat(new int[]{3,4,1,5,6,2,7})));}
}相关文章:

【算法】单调栈问题
文章目录 题目思路分析代码实现 题目 给定一个不含有重复值的数组arr,找到每一个i位置左边和右边离i位置最近且值比arr[i]小的位置,返回所有位置相应的消息。 比如arr{3,4,1,5,6,2,…...
Hack The Box - 关卡Dancing
SMB(全称是Server Message Block)是一个协议名,可用于在计算机间共享文件、打印机、串口等,电脑上的网上邻居就是靠它实现的。 SMB 是一种客户机/服务器、请求/响应协议。通过 SMB 协议,客户端应用程序可以在各种网络环境下读、写服务器上的…...
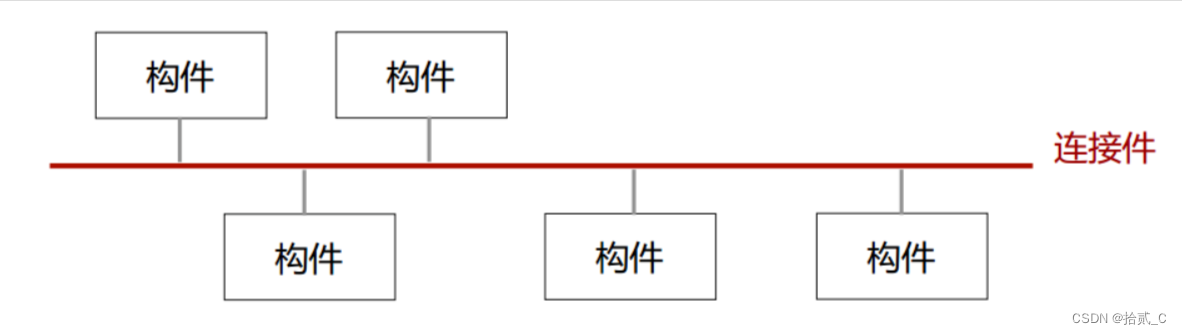
【软件设计与体系结构】 软件体系结构风格
软件体系结构(Software Architecture) 软件体系结构(Software Architecture)包括构成系统的设计元素的描述、 设计元素 之间的交互、 设计元素的组合模式以及在这些模式中的约束。 定义 软件体系结构表示系统的框架结构…...

detectron2 使用教程
本范例演示使用非常有名的目标检测框架detectron2 🤗🤗 在自己的数据集(balloon数据)上训练实例分割模型MaskRCNN的方法。 detectron2框架的设计有以下一些优点: 1,强大:提供了包括目标检测、实例分割、全景分割等非常广泛的视觉任务模型库。 2,灵活:可以通过注册机…...

哈希表常用数据结构
哈希表常用数据结构 查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。 哈希法也是空间换时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。 集合底层实现…...

Java字节流
4 字节流 字节流抽象基类 InputStream:这个抽象类是表示字节输入流的所有类的超类OutputStream:这个抽象类是表示字节输出流的所有类的超类子类名特点:子类名称都是以其父类名作为子类名的后缀4.1 IO流概述和分类 IO流概述: IO: 输入/输出(Input/Output)流:是一种抽象概念…...

arm3399主板-使用ubuntu20.04搭建LVS-DR(netplan)
目录 一、规划 1、网络拓扑 2、检查 二、配置设备 1、配置LVS 1.配置IP转发 2.清除防火墙 3.安装ipvsadm工具 4.配置VIP 5.netplan与NetworkManager介绍 6.添加LVS规则 1.清除防火墙 2.添加伪装IP 3.安装web服务 4. 修改内核参数,防止IP冲突 3、配置w…...
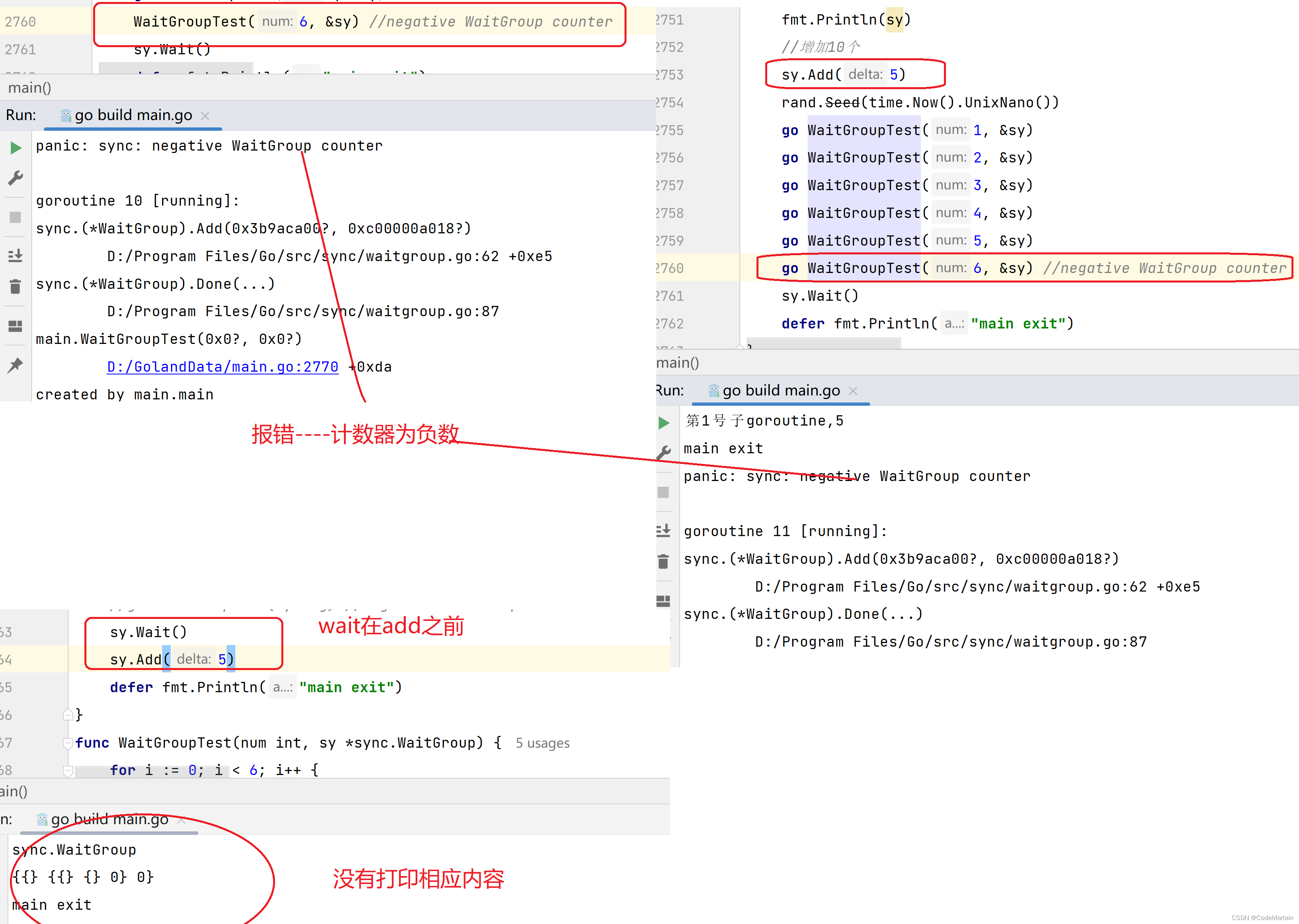
Go中同/异步与锁的应用~~sync包
Go中锁的实现~~sync包 go中sync包中提供了互斥锁; 在前面Go中channel文章中我们使用了time.Sleep()函数使得main函数的Goroutine阻塞至所有协程Goroutine结束,但这并不是一个很好的办法,因为我们实际应用中并不能准确知道协程什么时候结束(这里面要考虑服务器的性能,网络波动以…...

Flask知识点2
1、flash() get_flashed_messages() : 用来消耗flash方法中存储的消息 使用flash存储消息时,需要设置SECRET_KEY flash 内部消息存储依赖了session 2、CSRF(Cross Site Request Forgery) 跨站请求伪造,指攻击者盗用你的身份发送恶意请求 CSRFProt…...

R语言生物群落(生态)数据统计分析与绘图(从数据整理到分析结果展示)
R 语言作的开源、自由、免费等特点使其广泛应用于生物群落数据统计分析。生物群落数据多样而复杂,涉及众多统计分析方法。以生物群落数据分析中的最常用的统计方法回归和混合效应模型、多元统计分析技术及结构方程等数量分析方法为主线,通过多个来自经典…...
代码随想录训练营Day58| 739. 每日温度 496.下一个更大元素 I
目录 学习目标 学习内容 739. 每日温度 496.下一个更大元素 I 学习目标 739. 每日温度 496.下一个更大元素 I 学习内容 739. 每日温度 739. 每日温度 - 力扣(LeetCode)https://leetcode.cn/problems/daily-temperatures/ class Solution:def da…...
设计模式-命令模式
命令模式 问题背景命令模式基本介绍UML类图 解决方案UML类图代码示例 问题背景 1)随着现在科技越来越先进,我们在家庭中对物品的开关都不需要亲自走过去来进行了。我们只需要通过手机APP中的按键来远程执行这个命令。 2)其实这就是命令模式&…...

软考——下午题部分,例题一,二,三,六
例题一 11年上半年 病人,护理人员,医生 D 生命体征范围文件 日志文件 病历文件 治疗意见文件 14年上 E1 巴士司机,2 机械师,3 会计,4 主管,5 库存管理系统 D 巴士列表文件 维修记录文件 部件清单 人事档案 14年下 1 客户 2 供应商 D 销售订单表 库存…...
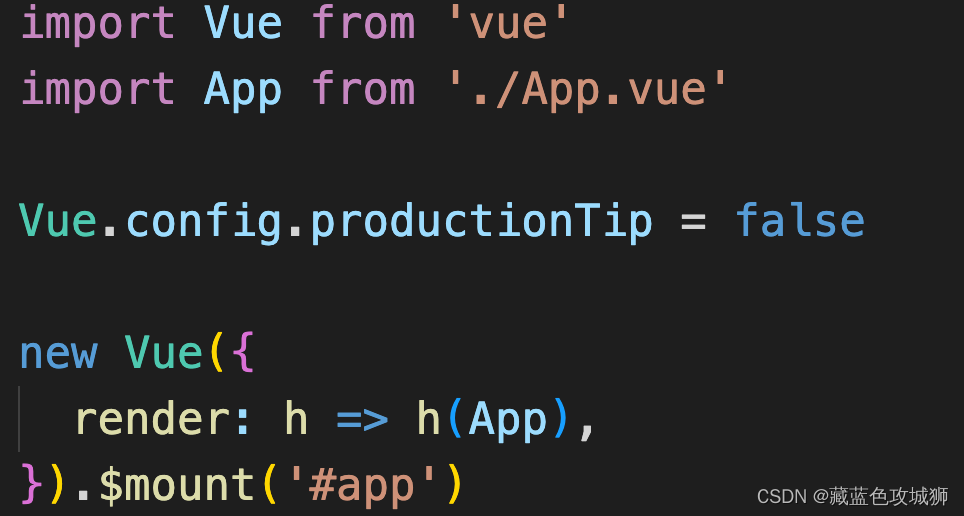
关于render: h => h(App)的解释
当我们第一次安装完脚手架,打开 的时候,我相信,一定有小伙伴和我一样,看到main.js里面的render: h > h(App),感觉懵懵的。 因为,在刚开始接触vue的时候,我们这里是这样写的: 而使用了脚手…...

flask实现简易图书管理系统
项目结构 技术选型 flask 做后端, 提供数据和渲染html 暂时没有提供mysql, 后续会更新操作mysql和样式美化的版本 起一个flask服务 flask是python的一个web框架, 下面演示如何提供http接口, 并返回json数据 main.py # flask创建http接口 from flask import Flask, request, jso…...
全国总决赛获奖名单)
2021 年全国大学生物联网设计竞赛(华为杯)全国总决赛获奖名单
由全国高等学校计算机教育研究会主办,上海交通大学承办,华为技术有限 公司协办,中国电信天翼物联、中国移动中移物联网、霍尼韦尔 Tridium、CSA 联盟、新大陆、德州仪器 (TI)、百度、机械工业出版社华章公司联合支持的 2021 全国大学生物联网…...

操作系统复习2.3.5-管程
引入管程 PV操作困难,容易书写出错,引入管程,作为一种高级同步机制 组成 局限于管程的共享数据结构说明对该数据结构进行操作的一组过程对局部于管程的共享数据结构设置初始值的语句管程有一个名字 基本特征 局限于管程的数据只能被局限…...

List Set Map Queue Deque 之间的区别是什么?
List Set Map Queue Deque 之间的区别是什么? 1. Java 集合框架有那些接口?2. List Set Map Queue Deque 之间的区别是什么? 1. Java 集合框架有那些接口? List、Set、Map、Queue、Deque 2. List Set Map Queue Deque 之间的区别…...

unity行为决策树实战详解
一、行为决策树的概念 行为决策树是一种用于游戏AI的决策模型,它将游戏AI的行为分解为一系列的决策节点,并通过节点之间的连接关系来描述游戏AI的行为逻辑。在行为决策树中,每个节点都代表一个行为或决策,例如移动、攻击、逃跑等…...

Spring学习记录
目录 bean的单例与多例 设置 工厂模式的三种形态 简单工厂模式 代码: 运行结果: 总结: 工厂模式 代码: 运行结果: 总结: 抽象工厂模式 代码: 运行结果: 总结: …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
