【算法】Transform to Chessboard 变为棋盘
Transform to Chessboard 变为棋盘
问题描述:
一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动,你能任意交换两列或是两行的位置。
返回 将这个矩阵变为 棋盘 所需的最小移动次数 。如果不存在可行的变换,输出 -1。
棋盘 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。
n的范围 [ 2,30]
分析
这是一个比较难想的问题,NN的矩阵中要把矩阵通过相邻行或者相邻列交换的方式,最终变成棋盘。
因为限定了必须是相邻行或者相邻列,所以有些特性就必须先抽出来。
当进行swap row时,同一列的元素是不变的,同理swap col时,同一行的元素也是不变的。
让n=2,很明显要是能最终变成棋盘,这2行的元素一定是满足01互补的,其次还会满足10交替或者01交替。
以行为角度,其必须满足只有2种类型的行,而且他们一定是互补的。其次 每一列 和每一行的01数量要满足其对应的棋盘。
因此需要解决的2个问题
1 最终能否变成棋盘
2 如何变成棋盘要移动的最少次数。
需要先通过 必要条件的判断,保证 矩阵最终可以变成棋盘,然后再对矩阵计算。
判断条件
1 行与列的种类必须是2,否则无解
2 A行的0数量一定与B行中1数量相等,
3 n为odd时,1开头,cnt1-cnt0=1,0开头 cnt0-cnt1=1。
n为even时,cnt1=cnt0
如果满足以上条件,说明矩阵最终可以变成棋盘。
而过程,可以是先行后列,或者先列后行,并且实际上只需要考虑第一行和第一列的移动次数。
对于第一行,0或者1开头,一旦第一行移动完成01间隔,为了实现01间隔,实际操作的是相邻列的移动,那么列就已经固定。
同理对于第一列,也是一样。
因为n的范围不超过30,可以利用位运算,将每一行的01状态用数字x表示,同时将目标的状态用y表示。
x^y中1的数量表示需要交换的行/列数。
因为最终的结果是0或者1开头,预设最终结果为tar 以1开头,对于row来说,有2种类型,r1,r2最终变成tar的移动次数可能不一样,最理想的一定是选移动次数最小的,对于col来说,也是一个道理。
代码
class Solution {int n = 0, INF = 0x3f3f3f3f;int getCnt(int a, int b) {return Integer.bitCount(a) != Integer.bitCount(b) ? INF : Integer.bitCount(a ^ b) / 2;}public int movesToChessboard(int[][] g) {n = g.length;int r1 = -1, r2 = -1, c1 = -1, c2 = -1, mask = (1 << n) - 1;for (int i = 0; i < n; i++) {int a = 0, b = 0;for (int j = 0; j < n; j++) {if (g[i][j] == 1) a += (1 << j);if (g[j][i] == 1) b += (1 << j);}if (r1 == -1) r1 = a;else if (r2 == -1 && a != r1) r2 = a;if (c1 == -1) c1 = b;else if (c2 == -1 && b != c1) c2 = b;if (a != r1 && a != r2) return -1;if (b != c1 && b != c2) return -1;}if (r2 == -1 || c2 == -1) return -1;if ((r1 ^ r2) != mask || (c1 ^ c2) != mask) return -1;int t = 0;for (int i = 0; i < n; i += 2) t += (1 << i);int ans = Math.min(getCnt(r1, t), getCnt(r2, t)) + Math.min(getCnt(c1, t), getCnt(c2, t));return ans >= INF ? -1 : ans;}
}时间复杂度 O( N 2 N^2 N2)
空间复杂度: O(1)
代码 来源于 三叶大佬,值得学习
Tag
Array Matrix Bit
相关文章:

【算法】Transform to Chessboard 变为棋盘
文章目录 Transform to Chessboard 变为棋盘问题描述:分析代码 Transform to Chessboard 变为棋盘 问题描述: 一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动,你能任意交换两列或是两行的位置。 返回 将这个矩阵变为 棋盘 所需…...

vue通过封装$on定义全局事件
我们先在vue项目的src跟目录下创建一个文件夹 叫 utils 下面创建一个js文件夹 叫 bus.js 参考代码如下 import Vue from "vue"; export default new Vue();然后 我们就可以来用了 在需要定义事件的组件中编写 <template><div><h1>Hello world!&…...

资产管理规范
生产系统资产管理规范 1. 引言 生产系统的资产管理是确保生产系统正常运行和提高生产效率的关键因素之一。本文档旨在制定一套规范,以确保生产系统中的资产,包括服务器和软件等,得到有效管理和保护。 2. 资产分类 生产系统资产可根据其性质…...
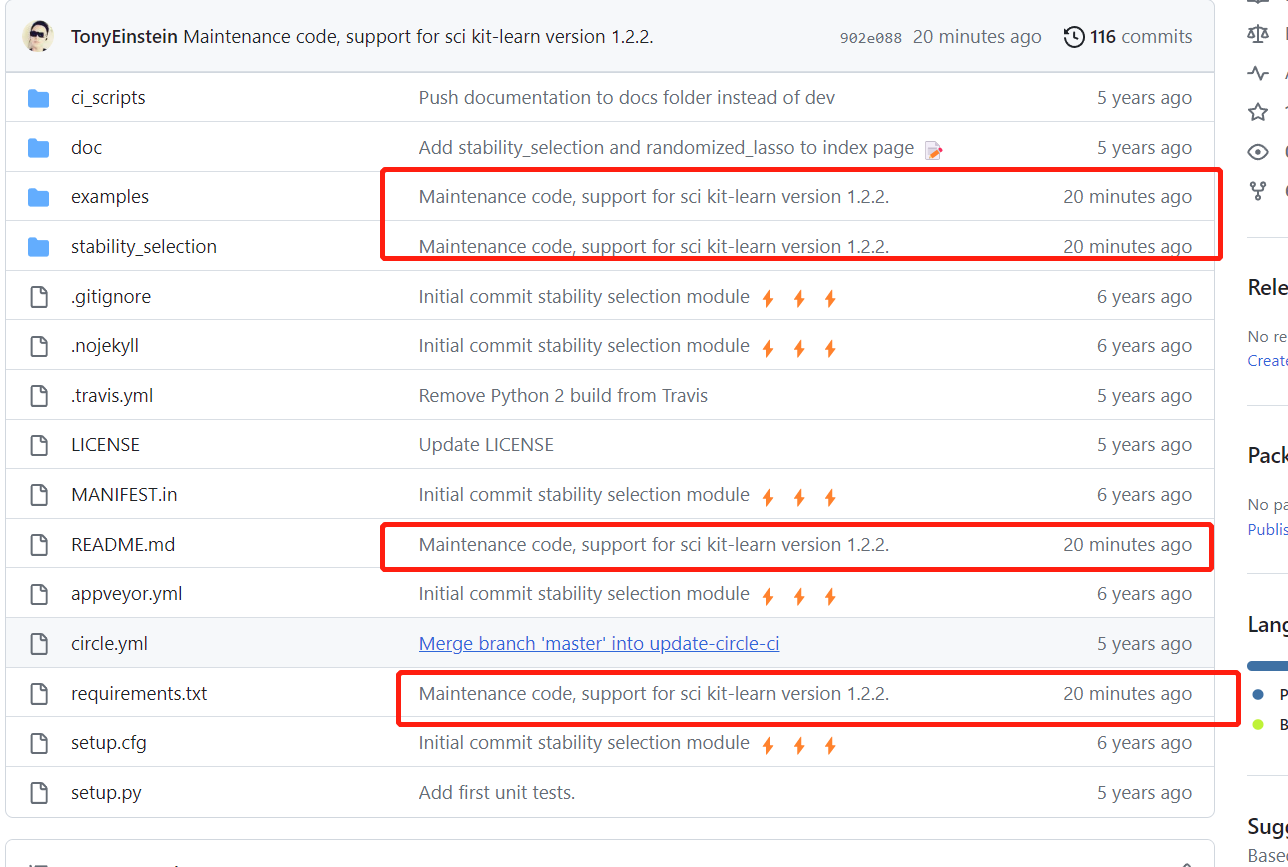
已解决:如何从别人的仓库那里克隆到自己的仓库,并修改代码并提交。
一、场景 拉取项目代码后,如果要共同开发一个项目的自动化代码,此时需要把自己写的代码部分提交到代码仓库。 可以用pycharm把修改的代码push到代码仓库 二、操作方法 1.从别人的仓库那里点击fork,将仓库克隆到自己的仓库。 2.在pychar…...
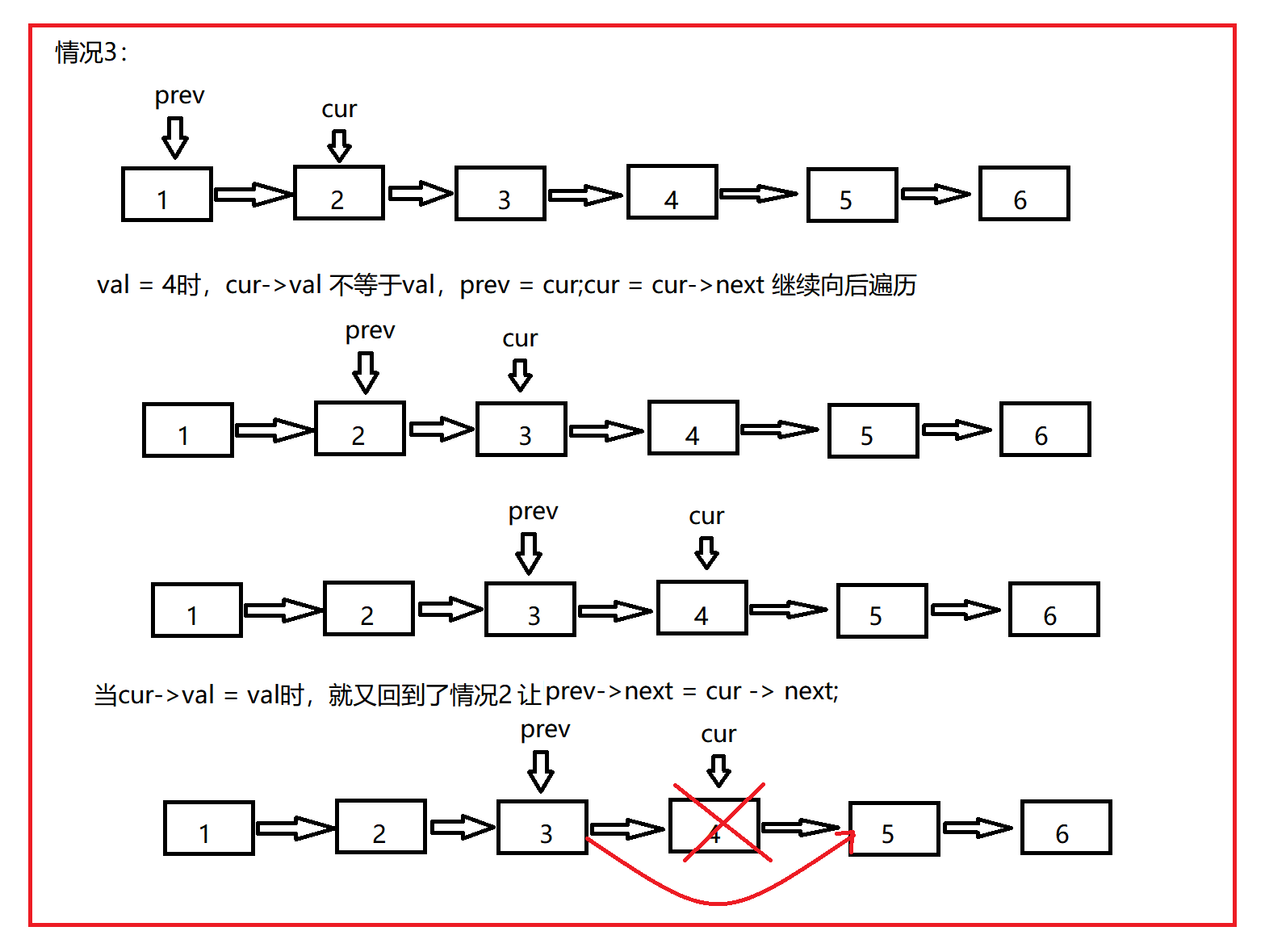
剑指 Offer 18. 删除链表的节点
🚀 作者简介:一名在后端领域学习,并渴望能够学有所成的追梦人。 🚁 个人主页:不 良 🔥 系列专栏:🛸剑指 Offer 📕 学习格言:博观而约取,厚积而薄…...

WiFi 6 vs WiFi 5
在现代无线通信领域,WiFi已经成为人们日常生活中不可或缺的一部分。随着技术的不断发展,WiFi标准也在不断更新和演进。WiFi 6(802.11ax)和WiFi 5(802.11ac)是当前两个主要的WiFi标准。 本文将详细介绍WiFi …...

PHP语言基础
一.标记风格 标记风格分为四类(推荐XML) 1.XML风格 <?php echo这是xml风格‘; ?> 注意:结束标识符必须单独另起一行,并且不能有空格。在标识符前后有其他符号或者字符也会发生错误。 2.脚本风格 <script languagephp> …...

怎么用Excel VBA写一个excel批量合并的程序?
您可以按照以下VBA代码来实现把同一路径上的所有工作簿合并到同一个工作簿中: VBA Option Explicit Sub MergeWorkbooks() Dim path As String, fileName As String, sheet As Worksheet Dim targetWorkbook As Workbook, sourceWorkbook As Workbook Dim workshe…...

WuThreat身份安全云-TVD每日漏洞情报-2023-05-22
漏洞名称:Apple WebKit 任意代码执行漏洞 漏洞级别:中危 漏洞编号:CVE-2023-32373 相关涉及:Apple iOS和iPadOS 16.4.1 漏洞状态:在野 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-12579 漏洞名称:海康威视部分iVMS系统存在文件上传漏洞 漏洞级别:未定义…...
Eclipse教程 Ⅵ
今天分享Eclipse Java 构建路径、Eclipse 运行配置(Run Configuration)和Eclipse 运行程序 Eclipse Java 构建路径 设置 Java 构建路径 Java构建路径用于在编译Java项目时找到依赖的类,包括以下几项: 源码包项目相关的 jar 包及类文件项目引用的的类…...
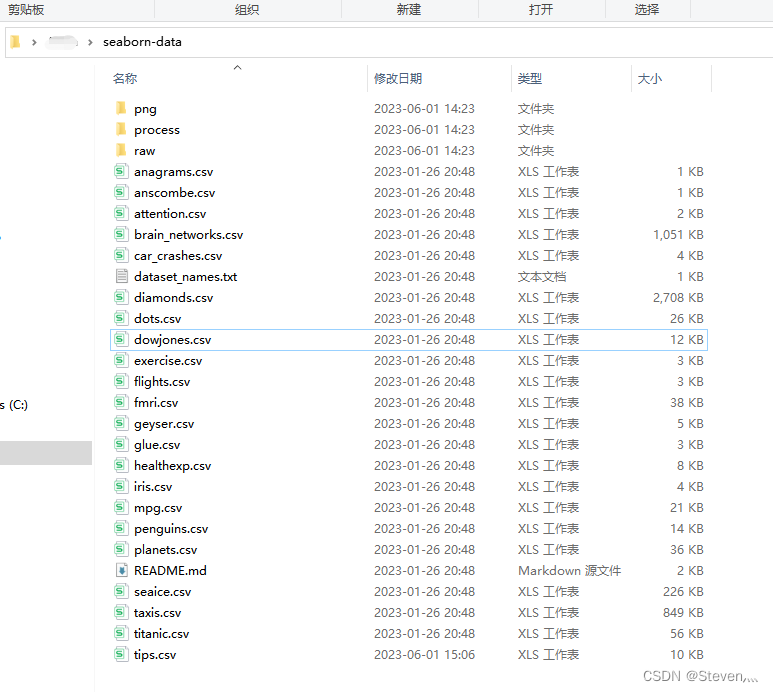
Seaborn.load_dataset()加载数据集失败最佳解决方法
load_dataset() 是 Seaborn 库中提供的一个函数,用于加载一些原始数据集。这些数据集包含了许多经典的数据集,比如鸢尾花数据集、小费数据集等,这些数据集在数据可视化和机器学习中非常常见。 使用 load_dataset() 函数可以方便地获取这些数…...
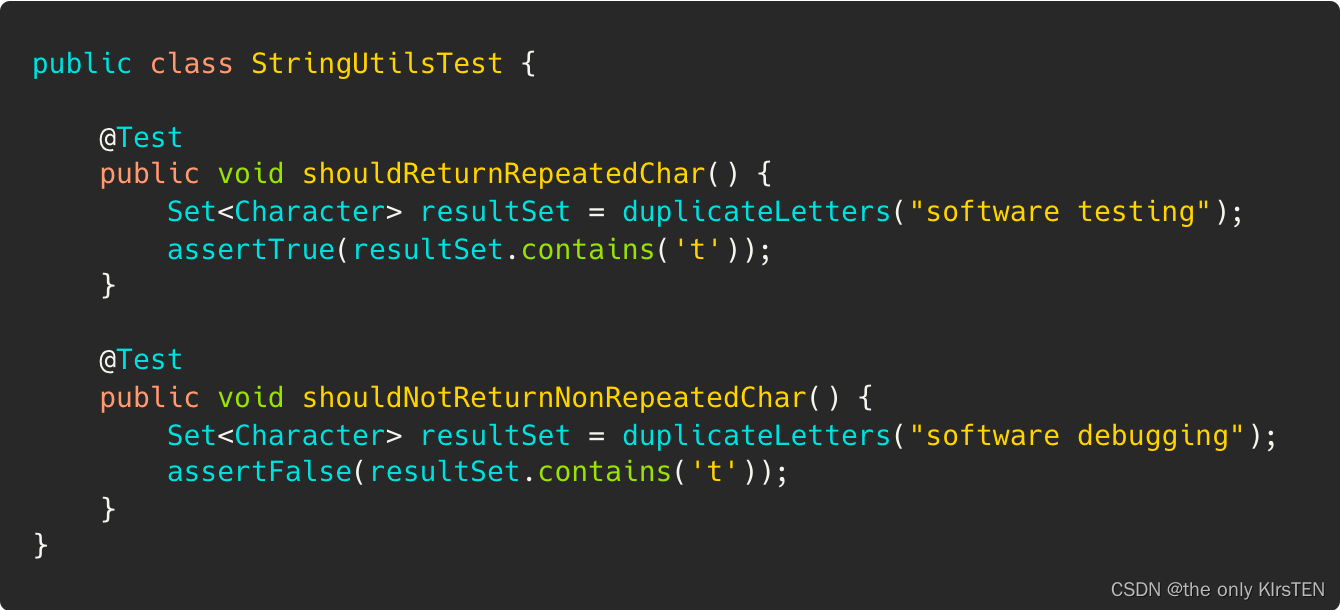
java 区分缺陷Defects/感染Infections/失败Failure
java 区分缺陷Defects/感染Infections/失败Failure 缺陷Defects 软件故障总是从代码中一个或多个缺陷的执行开始。 缺陷只是一段有缺陷、不正确的代码。 缺陷可能是程序语句的一部分或完整部分,也可能对应于不存在但应该存在的语句。 尽管程序员要对代码中的缺陷负…...
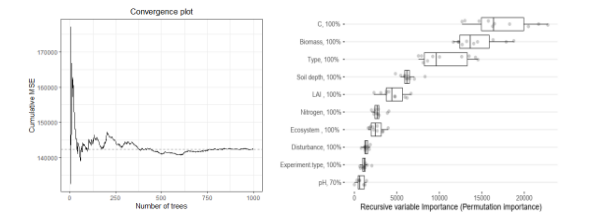
如何学习R-Meta分析与【文献计量分析、贝叶斯、机器学习等】多技术融合?
专题一:Meta分析的选题与文献计量分析CiteSpace应用 1、Meta分析的选题与文献检索 1) 什么是Meta分析 2) Meta分析的选题策略 3) 文献检索数据库 4) 精确检索策略,如何检索全、检索准 5) 文献的管理与清洗,如何制定文献纳入排除标准 6…...
分布式锁的应用场景与分布式锁实现(二):基于Redis实现分布式锁
分布式锁的应用场景与分布式锁实现(一):传统锁处理并发及传统锁的问题 基于Redis实现分布式锁 所有代码已同步到GitCode:https://gitcode.net/ruozhuliufeng/distributed-project.git 基本实现 借助Redis中的命令setnx(key&a…...

【JavaSE】Java基础语法(四十二):NIO
文章目录 1. 概述2. NIO与BIO的区别3. NIO三大模块4. NIO创建缓冲区对象【应用】5. NIO缓冲区添加数据【应用】6. NIO缓冲区获取数据【应用】7. 小结 1. 概述 BIO Blocking IO,阻塞型IONIO No Blocking IO,非阻塞型IO阻塞IO的弊端 在等待的过程中,什么事也做不了非阻塞IO的好处…...

Linux---systemctl
1. systemctl命令 Linux系统很多软件(内置或第三方)均支持使用systemctl命令控制:启动、停止、开机自启。 能够被systemctl管理的软件,一般也称之为:服务 语法:systemctl start | stop | status | enabl…...

零钱兑换,凑零钱问题,从暴力递归到动态规划(java)
凑零钱问题,从暴力递归到动态规划 leetcode 322 题 零钱兑换暴力递归(这个会超时,leetcode 跑不过去)递归缓存动态规划优化暴力递归动态规划专题 leetcode 322 题 零钱兑换 322 零钱兑换 - 可以打开链接测试 给你一个整数数组 c…...

Vue登录界面精美模板分享
文章目录 🐒个人主页🏅Vue项目常用组件模板仓库📖前言:🎀源码如下: 🐒个人主页 🏅Vue项目常用组件模板仓库 📖前言: 本篇博客主要提供vue组件之登陆组件源码…...
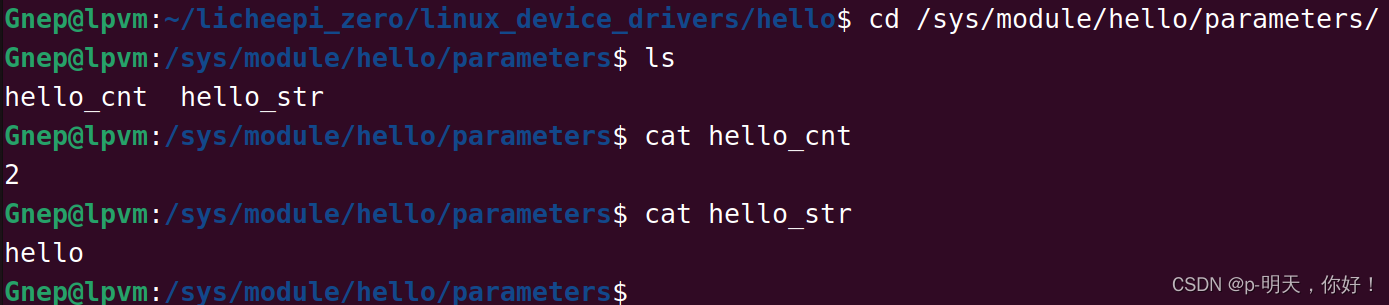
Linux设备驱动程序(二)——建立和运行模块
文章目录 前言一、设置测试系统二、Hello World 模块1、代码详解2、执行效果 三、内核模块相比于应用程序1、用户空间和内核空间2、内核的并发3、当前进程4、几个别的细节 四、编译和加载1、编译模块2、加载和卸载模块3、版本依赖 五、内核符号表六、预备知识七、初始化和关停1…...

【算法】单调栈问题
文章目录 题目思路分析代码实现 题目 给定一个不含有重复值的数组arr,找到每一个i位置左边和右边离i位置最近且值比arr[i]小的位置,返回所有位置相应的消息。 比如arr{3,4,1,5,6,2,…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
