【学习笔记】DFA的构造
虽然平时做过但是考场上肯定还是不会,不过没事干还是写一下吧
Myhill-Nerode\text{Myhill-Nerode}Myhill-Nerode 定理:给定一个语言LLL,定义在字符串上一个关系为,若对于所有的zzz,xzxzxz在LLL中当且仅当yzyzyz在LLL中,则称x,yx,yx,y在同一个等价类中。因此它把所有有限字符串的集合划分成一个或多个等价类。
Myhill-Nerode\text{Myhill-Nerode}Myhill-Nerode 定理声称在LLL的最小自动机中状态的数目等价于在LLL中诱导出的等价类的数目。
容易发现,语言LLL可以被有限状态机接受,当且仅当等价类的数目是有限的。
Gym 102586J
考虑用等价类构造DFADFADFA,还要为每一类找一个代表元。这里必须指出的是,LLL中的字符串一定在同一个等价类中,这个等价类也是接收点。
这里假定有限字符串集合长度不超过LLL,然后暴搜求出每个字符串的等价类即可。
如何证明取L=10L=10L=10的正确性?思维小实验
假设存在一个DFADFADFA d(k)d(k)d(k)能正确识别长度不超过kkk的好串,据此可以构造出一个NFANFANFA能正确识别长度不超过k+2k+2k+2的好串(其构造方法是,在原DFADFADFA的基础上建立ϵ\epsilonϵ,然后建一个子DFADFADFA表示操作的长度为333的段,再用ϵ\epsilonϵ连回在原DFADFADFA中所对应的字符边即可),再将其转化为DFADFADFA d(k+2)d(k+2)d(k+2)(最常用的方法是幂极构造),并最小化。
如果d(k)d(k)d(k)等价于d(k+2)d(k+2)d(k+2),我们就能得到d(k)=d(k+2)=d(k+4)=⋯d(k)=d(k+2)=d(k+4)=\cdotsd(k)=d(k+2)=d(k+4)=⋯ ,这也就是我们所要求的DFADFADFA。验证即可。
CF956F
考虑构造一个FAFAFA来识别不超过nnn位的f(m)≤kf(m)\le kf(m)≤k的数字串
FAFAFA的状态是背包容量,字母表是0∼90\sim 90∼9,原来状态是ccc,读入一个数字ddd,可以转移到c+dc+dc+d和∣c−d∣|c-d|∣c−d∣,显然这是一个NFANFANFA,可以设置状态数为100100100,然后大力幂集转移。
可以用长度为100100100的bitset\text{bitset}bitset实现幂集,用一个哈希表记录某个bitset\text{bitset}bitset出现过没有。
理论复杂度O(2100)O(2^{100})O(2100)。这非常不科学。这种方法还是比较大胆的。
我完全没这个魄力好吧
#include<bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N=1e5+5;
int n,K,tot,to[N][10],c[100],len;
ll l,r,dp[N][20][10];
map<__int128,int>id;
__int128 has(bitset<100>&b){__int128 x=0;for(int i=99;i>=0;i--){x*=2;if(b[i])x++;}return x;
}
int dfs(bitset<100>&b){int x;if(id[has(b)])return id[has(b)];x=id[has(b)]=++tot;for(int i=0;i<10;i++){if(b._Find_first()<=i)dp[tot][0][i]=1;}for(int i=0;i<10;i++){bitset<100>b2=(b<<i)|(b>>i);for(int j=0;j<i;j++)if(b[j])b2[i-j]=1;to[x][i]=dfs(b2);}return x;
}
ll dfs2(int x,int y,int z){if(!z)return dp[y][x][K];if(x==0)return dp[y][0][K];ll res=0;for(int i=0;i<=c[x];i++){res+=dfs2(x-1,to[y][i],i==c[x]);}return res;
}
ll solve(ll x){len=0;while(x)c[++len]=x%10,x/=10;return dfs2(len,1,1);
}
int main(){bitset<100>e;e[0]=1;int T;cin>>T,dfs(e);for(int l=0;l<10;l++){for(int i=1;i<=18;i++){for(int j=1;j<=tot;j++){for(int k=0;k<10;k++){dp[j][i][l]+=dp[to[j][k]][i-1][l];}}} }while(T--){cin>>l>>r>>K;cout<<solve(r)-solve(l-1)<<"\n";}
}
相关文章:

【学习笔记】DFA的构造
虽然平时做过但是考场上肯定还是不会,不过没事干还是写一下吧 Myhill-Nerode\text{Myhill-Nerode}Myhill-Nerode 定理:给定一个语言LLL,定义在字符串上一个关系为,若对于所有的zzz,xzxzxz在LLL中当且仅当yzyzyz在LLL中…...
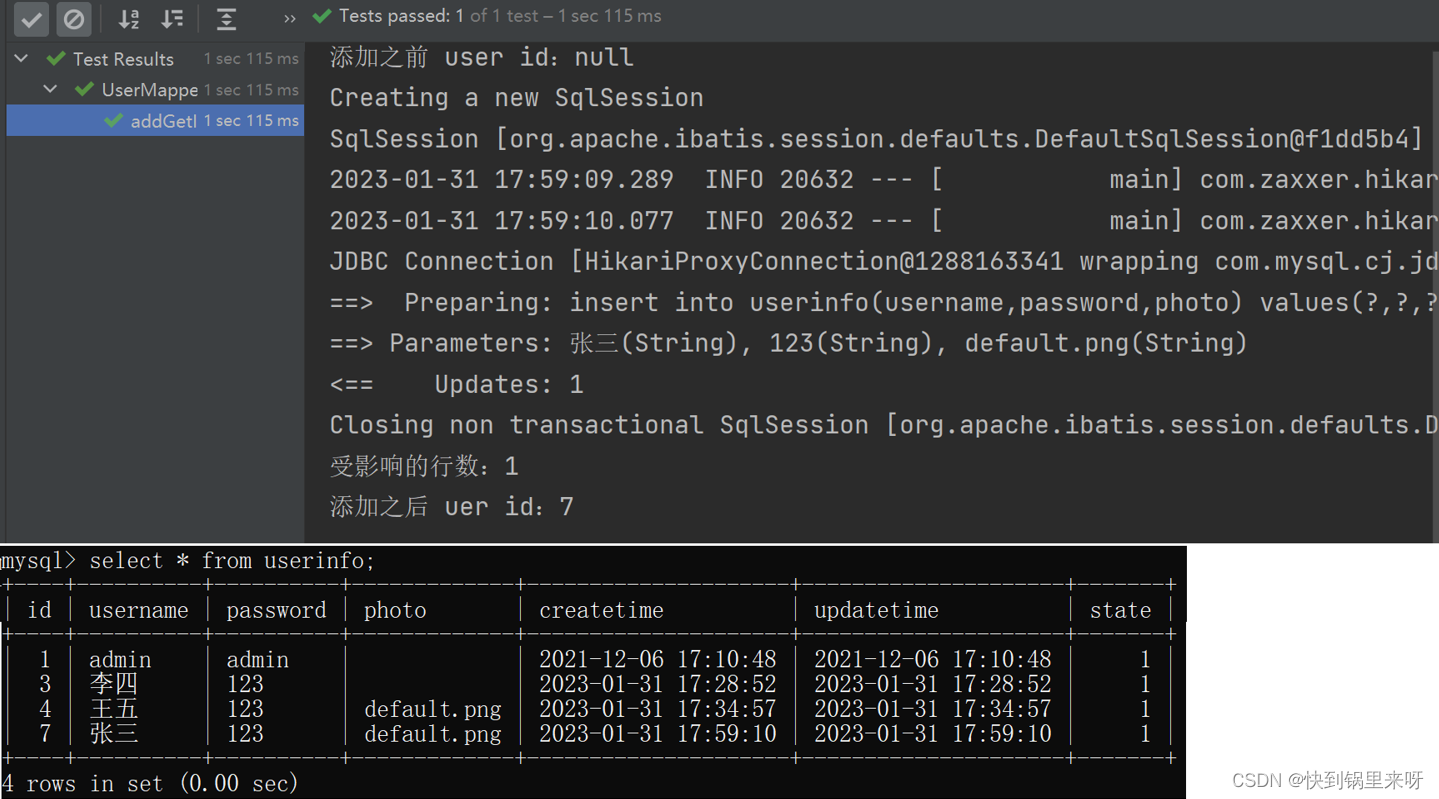
MyBatis 之二(增、删、改操作)
文章目录1. 修改操作1.1 在 mapper(interface)里面添加修改方法的声明1.2 在 XMl 中添加 <update> 标签和修改的 sql 代码1.3 在 UserMapper 中右键 Generate 点击 Test 生成 update 测试类2. 删除操作2.1 在 mapper (interface&#x…...
28k入职腾讯测试岗那天,我哭了,这5个月付出的一切总算没有白费~
先说一下自己的个人情况,计算机专业,16年普通二本学校毕业,经历过一些失败的工作经历后,经推荐就进入了华为的测试岗,进去才知道是接了个外包项目,不太稳定的样子,可是刚毕业谁知道什么外包不外…...
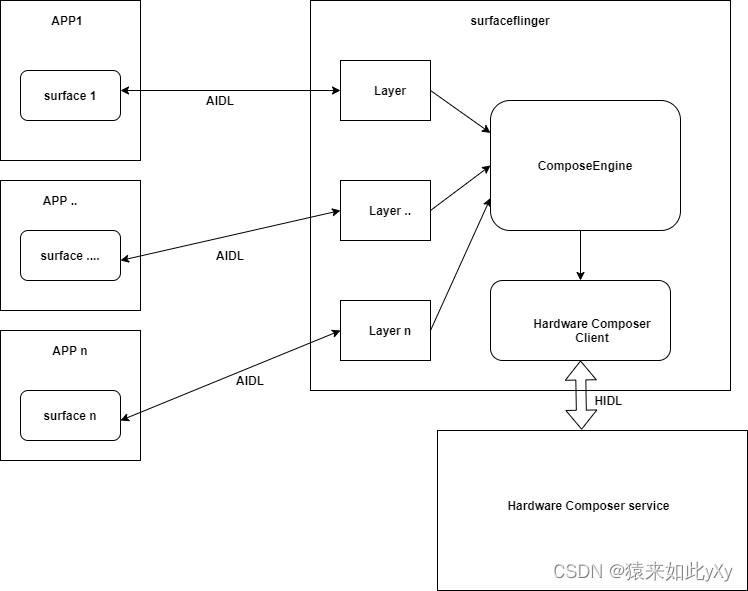
【surfaceflinger源码分析】surfaceflinger进程的消息驱动模型
概述 对于surfaceflinger大多数人都知道它的功能是做图形合成的,用英语表示就是指composite。其大致框图如下: 各个Android app将自己的图形画面通过surface为载体通过AIDL接口(Binder IPC)传递到surfaceflinger进程surfaceflinger进程中的composition engine与HW…...

「架构师」001计算机组成与体系结构
文章目录 前言一、计算机结构1.1 计算机组成结构1.2 CPU组成1.3 冯诺依曼结构与哈佛结构二、存储结构2.1 层次化存储结构2.2 Cache三、数据传输控制方式四、总线五、CISC与RISC六、流水线七、校验码八、嵌入式前言 本文主要介绍计算机组成与体系结构。 一、计算机结构 1.1 计…...
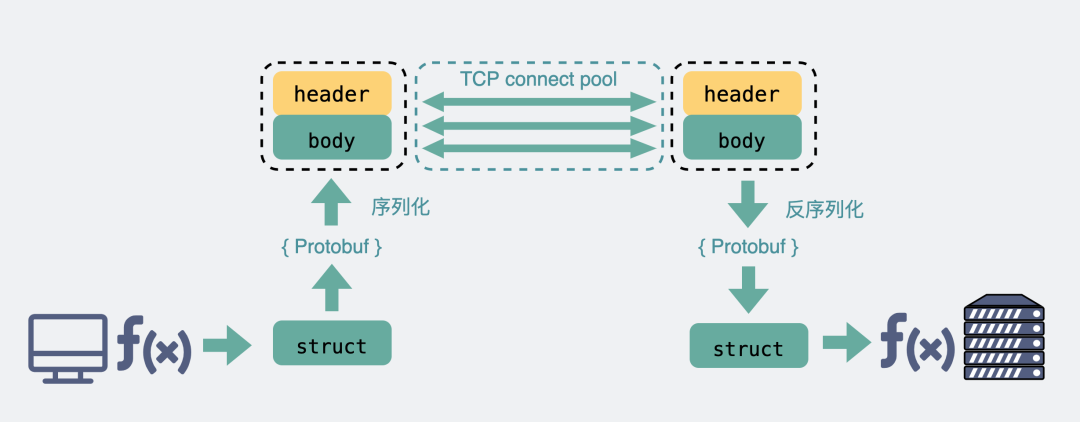
既然有HTTP协议,为什么还要有RPC
既然有HTTP协议,为什么还要有RPC? 从TCP聊起 作为一个程序员,假设我们需要在A电脑的进程发一段数据到B电脑的进程,我们一般会在代码里使用socket进行编程。 这时候,我们可选项一般也就TCP和UDP二选一。TCP可靠&…...
)
【新2023】华为OD机试 - 选座位(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 选座位 题目 疫情期间需要大家保证一定的社交距离 公司组织开交流会议,座位有一排共N个座位 编号分别为[0...n-1] 要求员工一个接着一个进入会议室 并且还可以在任何时候离开会议室 每当一个员工进入时…...

数据分析与SAS学习笔记4
INPUT语句:格式修饰符: “:” 修饰符。表示从下一个非空格列读入数据,直到:1 遇到再下一个空格列; 2 读到预先定义的变量长度; 3 数据行结束。哪个先出现就在哪儿结束。 “&” 修饰符。表示从下一个非空格列读入…...

Xepor:一款针对逆向工程和安全分析的Web路由框架
关于Xepor Xepor是一款专为逆向分析工程师和安全研究专家设计的Web路由框架,该工具可以为研究人员提供类似Flask API的功能,支持以人类友好的方式拦截和修改HTTP请求或HTTP响应信息。 该项目需要与mitmproxy一起结合使用,用户可以使用Xepor…...
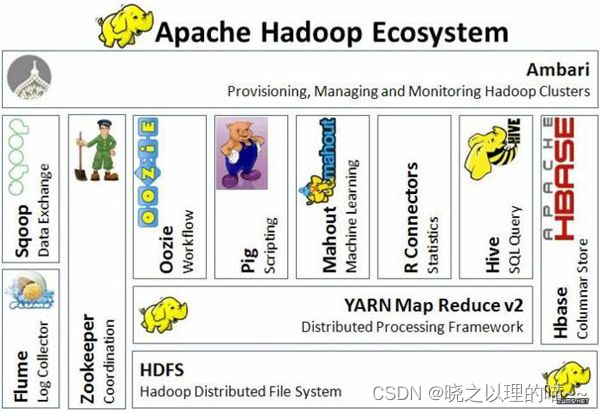
Hadoop核心组成和生态系统简介
一、Hadoop的概念 Hadoop是一个由Apache基金会所开发的分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。充分利用集群的威力进行高速运算和存储。Hadoop实现了一个分布式文件系统( Distributed File System)&am…...
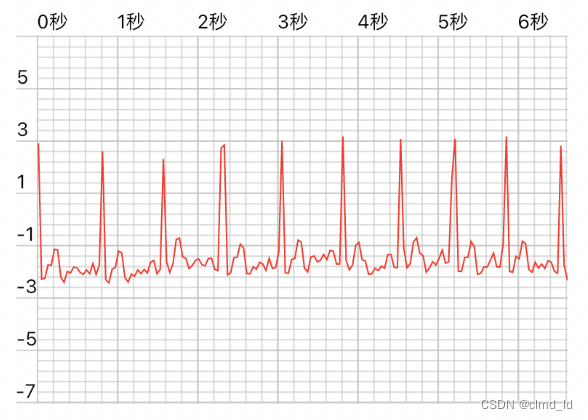
Flutter-Charts_painter大数据量绘制性能优化-数据收敛
Flutter-Charts_painter大数据量绘制性能优化-数据收敛 1、背景介绍 HRV测量仪器上传的数据,每秒有250个数据,业务上需要测量180秒,预计有3w-5w个数据点需要绘制到折线图上去。Charts_painter绘制这么大的数据是时候会有些卡顿,…...

使用 GeForce Experience 更新 NVIDIA GPU 显卡驱动
使用 GeForce Experience 更新 NVIDIA GPU 显卡驱动1. NVIDIA GeForce Experience 2. 驱动程序 -> 检查更新文件 3. 下载 如果有可用的新版驱动的话,点击后方的 [下载] 按钮即可。 4. 安装 [快速安装] 按照默认设置安装驱动,[自定义安装] 可以自行…...

Java泛型的<? super T>,<? extend T>的区别
? extends T ? extends T 描述了通配符上界, 即具体的泛型参数需要满足条件: 泛型参数必须是 T 类型或它的子类, 例如: List<? extends Number> numberArray new ArrayList<Number>(); // Number 是 Number 类型的 List<? extends Number>…...

如何做出好看的Excel可视化图表?
可视化死磕excel是不行的,作为数据分析行业的偷懒大户,分享一些我在可视化工具上的使用心得,总结了三大类:快速出图类、专业图表类、高端大屏类。个人经验,大家按需采纳: 一、快速出图类 如果你只是因为偶…...

智能吸吹一体式方案设计特点
一、家用吸吹一体吸尘器方案研发设计要素: 1.小巧的机身设计,一手掌握,无论是床底、沙发下还是家具缝隙之中都能够使用。 2.无线,插电两用,在家方便可插电使用。内置可充电锂电池,充满电也可无线使用。 3.采…...

CSDN 编辑器 Marddown 语法备忘
原文链接:https://blog.csdn.net/blogdevteam/article/details/103478461 本文对其二次加工,增加渲染样式、补充例程、添加未收录的常用语法。 CSDN Markdown 编辑器遵循 CommonMark spec 语法规范。 快捷键 撤销:Ctrl/Command Z 重做&…...

回归预测 | MATLAB实现NGO-BiLSTM北方苍鹰算法优化双向长短期记忆网络多输入单输出回归预测
回归预测 | MATLAB实现NGO-BiLSTM北方苍鹰算法优化双向长短期记忆网络多输入单输出回归预测 目录回归预测 | MATLAB实现NGO-BiLSTM北方苍鹰算法优化双向长短期记忆网络多输入单输出回归预测预测效果基本介绍程序设计参考资料预测效果 基本介绍 Matlab实现NGO-BiLSTM北方苍鹰算法…...
Linux——操作系统安装
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。个人爱好: 编程,打篮球,计算机知识个人名言:海不辞水,故能成其大;山不辞石…...
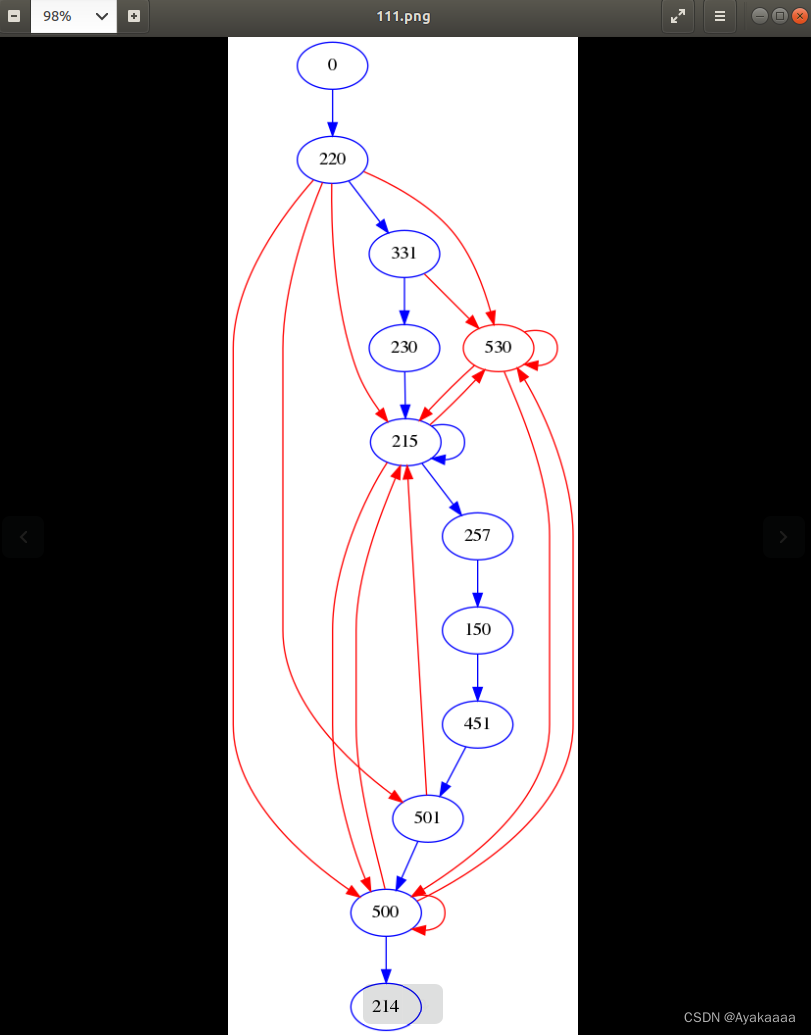
AFLNET lightftp项目报错解决方法
在学习AFLNET的时候,本人尝试对示例项目中的lightftp进行fuzz,而后出现如下报错: AFLNet - the states hashtable should always contain an entry of the initial state 在github项目issue里看到了有人的问题和我一摸一样,Stack Overflow里…...

av 146 003
121. 团队章程的目标是什么? A. 使团队正规化,以便能够清楚地了解资源分配和参与情况 B. 创造一个团队可以自我管理和自我指导的环境 C. 创造一个环境,使团队成员能够尽其所能地工作 D. 创造一种团队归属感,促进包容性和协作性的行为 12…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
