ARC140D One to One
ARC140D One to One
题目大意
对于一个长度为nnn的整数序列X=(x1,x2,…xn)X=(x_1,x_2,\dots x_n)X=(x1,x2,…xn),每个元素都在111到nnn之间,令f(X)f(X)f(X)表示以下问题的答案:
- 有一个nnn个顶点nnn条边的无向图(可能有重边和自环),第iii条边连接iii和XiX_iXi,求联通块的数量
给一个正整数nnn和一个长度为nnn的序列A=(a1,a2…an)A=(a_1,a_2\dots a_n)A=(a1,a2…an),其每一个元素都在111到nnn之间,或者为−1-1−1。
你可以将每个值为−1-1−1的aia_iai变为任意一个111到nnn之间的数,求所有情况下f(A)f(A)f(A)的和。输出答案对998244353998244353998244353取模。
题解
令kkk表示ai=−1a_i=-1ai=−1的元素的个数。
我们可以先将ai≠−1a_i\neq -1ai=−1的边连上,那么现在图上的每一个连通块都是树或环或基环树。
如果是树的话,则这个连通块有且只有一个ai=−1a_i=-1ai=−1的点
如果是环或基环树的话,则这个连通块没有ai=−1a_i=-1ai=−1的点
我们可以先把环和基环树的贡献算出来,每个环或基环树的贡献为nkn^knk,因为不管怎么连,环或基环树都会有111的贡献。那么如果有树向环或基环树连边,则这棵树不计算贡献。
树与环或基环树连边的贡献不需计算,那么我们只需要求树与树连边的贡献了。
因为每棵树只有一条边连出去,所以我们可以将每棵树看成一个点。
如果不连向环和基环树,那么这些树一定会形成一个环。对于一个顺序已确定的环,形成这样的环的方案数为∏sizi\prod siz_i∏sizi。
我们考虑DP。设fif_ifi表示形成长度为iii的环的方案数,那么对于每个点jjj,有转移式
fi=fi+fi−1×sizkf_i=f_i+f_{i-1}\times siz_kfi=fi+fi−1×sizk
求出fff后我们考虑如何计算答案。对于所有长度为iii的环的贡献为fi×(i−1)!×nk−if_i\times (i-1)!\times n^{k-i}fi×(i−1)!×nk−i。其中(i−1)!(i-1)!(i−1)!表示iii个点按不同顺序可以构成(i−1)!(i-1)!(i−1)!个不同的环,nk−in^{k-i}nk−i表示其他n−kn-kn−k个点可以任意连边。
这样问题就解决了,时间复杂度为O(n2)O(n^2)O(n2)。
code
#include<bits/stdc++.h>
using namespace std;
int n,tot=0,vt=0,a[2005],d[5005],l[5005],r[5005],s[2005],z[2005],siz[2005];
long long ans,f[2005],jc[2005],mi[2005];
long long mod=998244353;
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void dfs(int u){z[u]=1;siz[u]=1;for(int i=r[u];i;i=l[i]){if(!z[d[i]]){dfs(d[i]);siz[u]+=siz[d[i]];}}
}
int main()
{scanf("%d",&n);jc[0]=mi[0]=1;for(int i=1;i<=n;i++){jc[i]=jc[i-1]*i%mod;mi[i]=mi[i-1]*n%mod;}for(int i=1;i<=n;i++){scanf("%d",&a[i]);if(a[i]==-1) continue;add(i,a[i]);add(a[i],i);}for(int i=1;i<=n;i++){if(a[i]==-1){dfs(i);s[++vt]=siz[i];}}for(int i=1;i<=n;i++){if(!z[i]){dfs(i);ans=(ans+mi[vt])%mod; }}f[0]=1;for(int i=1;i<=vt;i++){for(int j=i;j>=1;j--) f[j]=(f[j]+f[j-1]*s[i]%mod)%mod;}for(int i=1;i<=vt;i++){ans=(ans+f[i]*jc[i-1]%mod*mi[vt-i]%mod)%mod;}printf("%lld",ans);return 0;
}
相关文章:

ARC140D One to One
ARC140D One to One 题目大意 对于一个长度为nnn的整数序列X(x1,x2,…xn)X(x_1,x_2,\dots x_n)X(x1,x2,…xn),每个元素都在111到nnn之间,令f(X)f(X)f(X)表示以下问题的答案: 有一个nnn个顶点nnn条边的无向图(可能有重边和…...

联合身份验证与Cognito
Hello大家好,我们接下来讨论AWS联合身份验证的内容。 AWS联合身份验证 对于考试,联合身份验证部分是一块非常重要的内容。那什么是联合身份验证,它是做什么用的呢? 联合身份验证,是用来允许AWS外部用户,如…...

day18_常用API之String类丶Object类
String概述 java.lang.String 类代表字符串,String类定义的变量可以用于指向字符串对象,同时String类提供了很多操作字符串的功能,我们可以直接使用。Java 程序中的所有字符串文字(例如“abc”)都为此类的对象 特点:St…...

OSG三维渲染引擎编程学习之五十五:“第五章:OSG场景渲染” 之 “5.13 一维纹理”
目录 第五章 OSG场景渲染 5.13 一维纹理 5.13.1 一维纹理介绍 5.13.2 一维纹理示例 第五章 OSG场景渲染 OSG存在场景树和渲染树,“场景数”的构建在第三章“OSG场景组织”已详细阐明,本章开始...
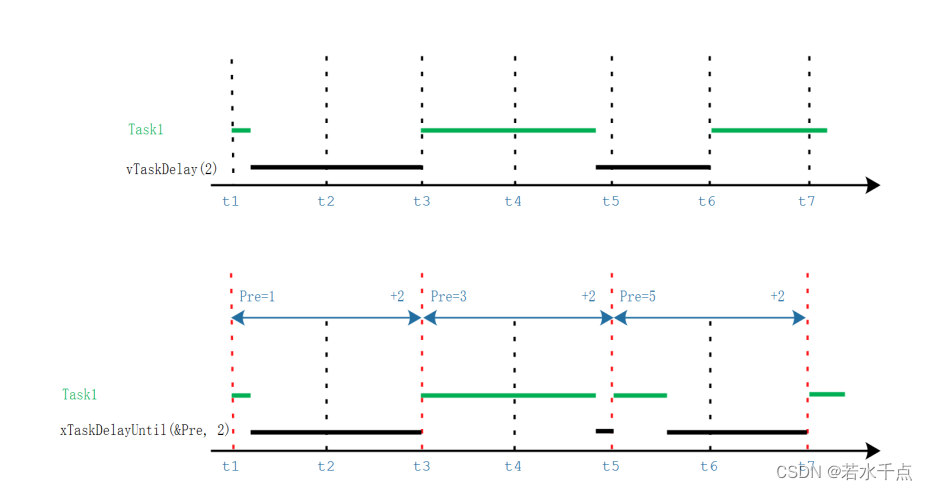
RTOS随笔之FreeRTOS启动与同步方法
RTOS启动与同步机制RTOS启动任务切换场景任务同步机制队列信号量事件组任务通知任务延时RTOS启动 FreeRTOS在任务创建完成后调用函数vTaskStartScheduler()启动任务调度器。 vTaskStartScheduler()任务启动函数详解 void vTaskStartScheduler( void ) {BaseType_t xReturn;xR…...
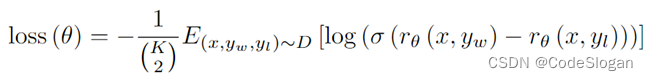
【AI/NLP】InstructGPT数据标注问题
文章目录1 背景介绍2 标记员筛选2.1 标记员筛选标准3 数据集及其标注3.1 预训练3.2 微调3.2.1 SFT-demonstration data3.2.2 RM-comparison data3.3 数据集大小4 模型实现1 背景介绍 ChatGPT的训练过程与InstructGPT相近,大致分为三步: SFT:…...
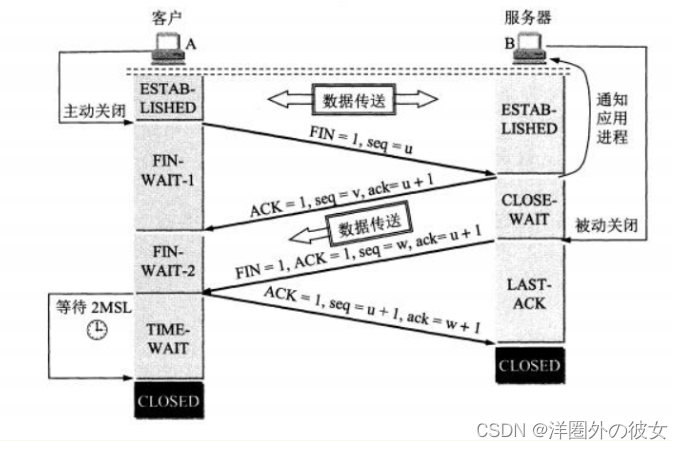
三次握手和四次挥手
文章目录TCP三次握手为什么要三次握手三次握手可以携带数据吗?三次握手失败,服务端会如何处理?ISN代表什么,意义,何要动态随机什么是半连接队列第2次握手传回了ACK,为什么还要传回SYN?为什么要四次挥手TCP…...
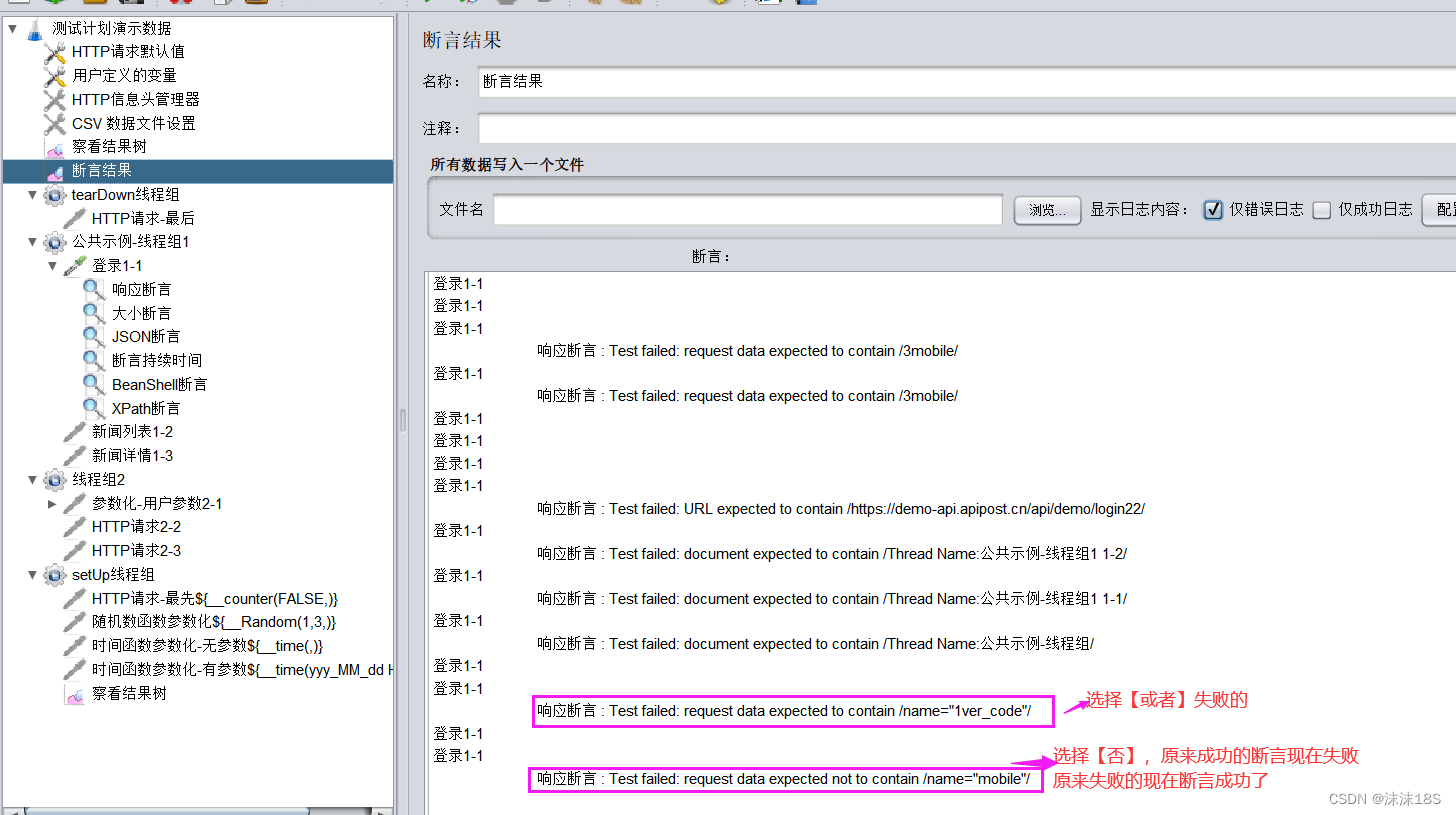
Jmeter常用断言之响应断言详解
响应断言是最常用的一种断言方法,主要是对响应结果中的文本内容进行断言,比如响应结果是否包含指定的值,或者是否等于指定的值。响应断言可以适用各种返回类型的响应结果,如:Test、html、application/json、applicatio…...
)
【Python学习笔记】36.Python3 MySQL - mysql-connector 驱动(1)
前言 MySQL 是最流行的关系型数据库管理系统,本章节为大家介绍使用 mysql-connector 来连接使用 MySQL, mysql-connector 是 MySQL 官方提供的驱动器。 Python3 MySQL - mysql-connector 驱动 我们可以使用 pip 命令来安装 mysql-connector࿱…...

计算机SCI论文课题设计需要注意什么? - 易智编译EaseEditing
课题设计就要本着严谨性和可行性来进行。实验设计的类型要选择准确,统计学的方法要运用合理,研究对象和观察指标的选择也要符合研究目的的要求,技术路线要清晰明了。 关于课题的设计的可行性也要综合考虑,比如前期的相关工作基础…...
Quartz入门教程
本文参考文章编写 Quartz 官网 Quartz 是 OpenSymphony 开源组织在 Job Scheduling 领域又一个开源项目,是完全由 Java 开发的一个开源任务日程管理系统,“任务进度管理器”就是一个在预先确定(被纳入日程)的时间到达时ÿ…...

TypeScript 学习之 function
函数可以实现抽象层,模拟类,信息隐藏和模块。 函数有:有名字的函数、匿名函数 在 JavaScript 中的函数 // 有名字的函数 function add(x, y) {return x y; }// 匿名函数 let myAdd function (x, y) {return x y; };函数类型 typescript 可…...

【云计算自学路线】
云计算包含的技术内容和涉及的方向比较多,一定要进行系统化的学习才能更好的掌握这门技术。 云计算作为互联网新技术领域,现阶段也是出于高速发展期,想学习加入云计算行业的小伙伴可以抓紧机会了,跟着小课一起来了解云计算以及它…...

code01 v2黑屏、花屏、死机、断电重启、休眠死机的进来
症状解决 长话简说,症状如下: 使用浏览器、播放视频等,遇到突然死机或花屏死机的情况 关闭硬件加速,如:浏览器中设置关闭硬件加速,出现这种症状的软件都需要设置 开机电流音、播放与暂停时喇叭吱吱想、打…...

分享107个HTML电子商务模板,总有一款适合您
分享107个HTML电子商务模板,总有一款适合您 107个HTML电子商务模板下载链接:https://pan.baidu.com/s/1VW67Wjso1BRpH7O3IlbZwg?pwd0d4s 提取码:0d4s Python采集代码下载链接:采集代码.zip - 蓝奏云 Aplustemplates 购物模板…...
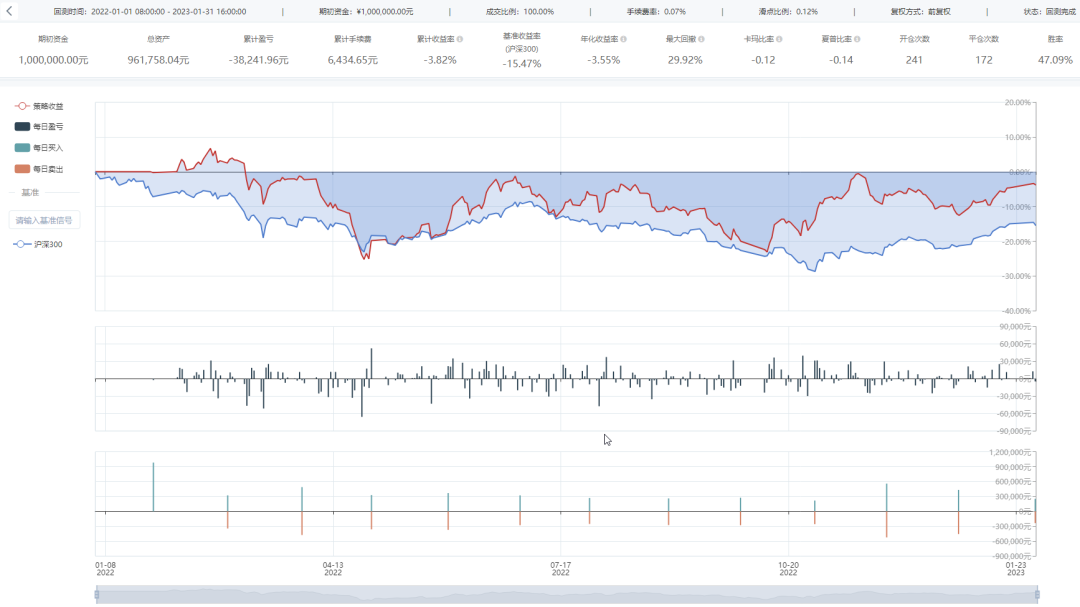
Barra模型因子的构建及应用系列三之Momentum因子
一、摘要 在之前的Barra模型系列文章中,我们已经初步讲解、构建了Size因子和Beta因子,并分别创建了对应的单因子策略。通过回测发现,其中Size因子的小市值效应具有很强的收益能力。而本篇文章将在该系列下进一步构建Momentum因子。 二、模型…...

8.2.1.3 索引合并优化
索引合并访问方法检索具有多个范围扫描的行,并将其结果合并为一个。此访问方法仅合并来自单个表的索引扫描,而不是跨多个表的扫描。合并可以生成其基础扫描的合并、交叉或交叉的合并。 可以使用索引合并的查询示例: SELECT * FROM tbl_name…...

水雨情在线小能手-雨量水位报警站
雨量水位报警站由水位探测器、雨量传感器、报警灯、扩音器、太阳能板和采集传输控制器组成。实时采集水位等级,三个水位探测器对应3个水位等级,当现场水面浸没相应探测器时,本机会实时发出语音报警,同时可发送相应的预警/报警等级…...
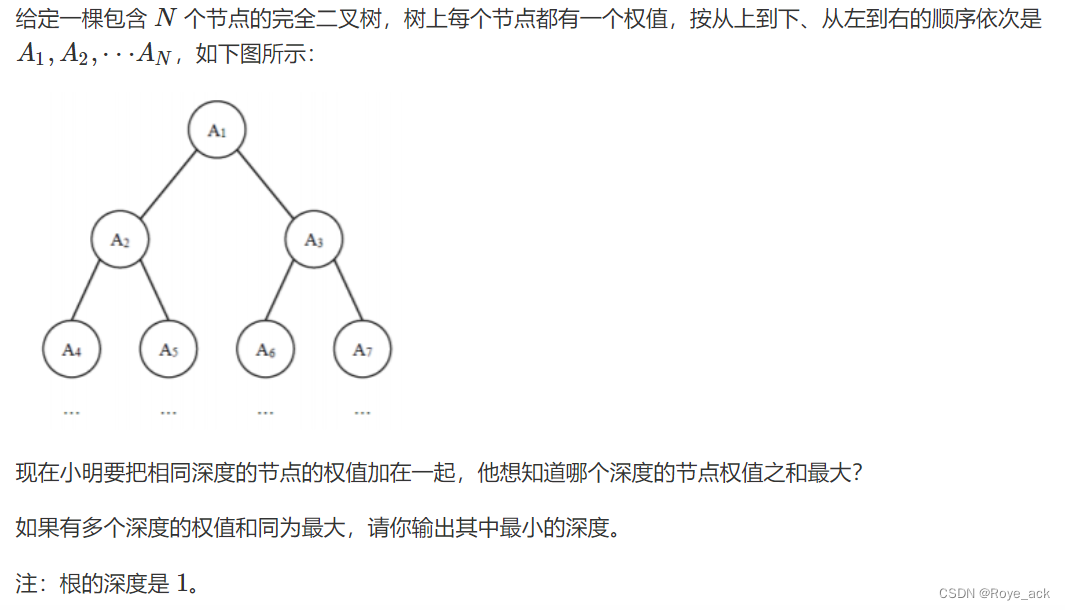
【蓝桥杯集训4】双指针专题(6 / 6)
目录 3768. 字符串删减 - 滑动窗口ac 799. 最长连续不重复子序列 - 滑动窗口 800. 数组元素的目标和 - 二分ac 2816. 判断子序列 - 双指针 1238. 日志统计 - 滑动窗口 1240. 完全二叉树的权值 - 双指针 1、前缀和 - 通过了 5/12个数据 2、双指针 3768. 字符串删减 -…...

文件流,gzip解压,压缩
目录 文件画布 写入 (空文件Foutnew File(Parent,entry.getName());)FileOutputStream outnew FileOutputStream(Fout);BufferedOutputStream Boutnew BufferedOutputStream(out);其他流量基于基础包装文件--文件流---字节流 顺序pbf一般是形成后再压缩目…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
