二叉树详解:带你掌握二叉树
目录
- 前言
- 1. 树型结构
- 1. 1 树的概念
- 1.2 树的特点
- 1.3 树的相关术语
- 2. 二叉树(binary tree)
- 2.1 二叉树的概念
- 2.2 二叉树中的特殊树
- 2.2.1 满二叉树
- 2.2.2 完全二叉树
- 2.3 二叉树的性质
- 3. 二叉树的遍历
- 3.1 前序遍历
- 3.2 中序遍历
- 3.3 后序遍历
- 3.4 层序遍历
- 总结
前言
因为二叉树是一种特殊的树,所以想要学习好二叉树,必须了解树型结构,知道树的基本概念。所以正式开始学习之前,在前面为大家引入了树的概念。
1. 树型结构
1. 1 树的概念
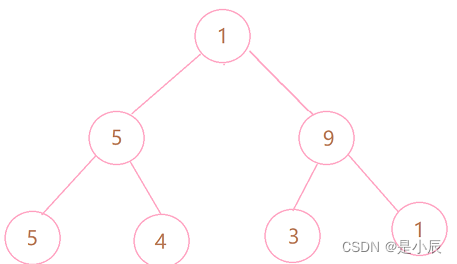
树是一种非线性的数据结构,它是有n个节点构成的集合,把它称为树,是因为这种结构看起来就像一个倒挂的树,根在上面,叶在下面。
1.2 树的特点
- 有一个特殊的节点,没有前驱节点,我们将此称为根节点。
- 树是递归定义的。
- 树的任何节点都可以有任意后继,但是它们不会交叉。
- 树是一个非线性数据结构。
1.3 树的相关术语
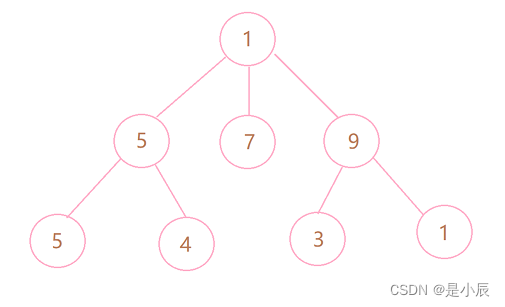
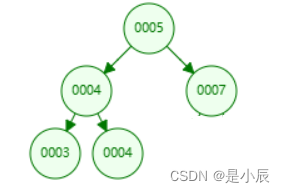
- 根节点:一个特殊节点,没有前驱节点;上图:第一个1 。
- 节点的度:一个节点拥有的子树的多少,就是该节点的度;上图:9的度为:2 。
- 树的度:一棵树最大节点的度就是树的度; 上图:最大的节点的度为3 ,则树的度为3 。
- 叶节点:又称叶子节点,终端节点,度为零的节点;上图:3、4等都是叶节点。
- 父节点:又称双亲节点,父亲节点,一个节点有子节点,则就是这是字节点的父节点;上图:9是3的父节点。
- 子节点:又称孩子节点,一个节点下面与连接的节点就是子节点;上图:3是9的子节点。
- 节点的层次:根节点为第一层,根节点的子节点为第二层,以此类推。
- 树的高度或深度:树中最大的节点的层次。
2. 二叉树(binary tree)
2.1 二叉树的概念
二叉树是一种树形数据结构,是一种特殊的树,二叉树中每个节点最多只能有两个子节点,并且二叉树的次序是不可颠倒的,是一颗有序树。
2.2 二叉树中的特殊树
二叉树是一种特殊的树,而特殊树中还会有特殊。
2.2.1 满二叉树
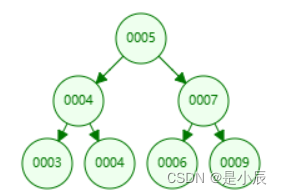
一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵
二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2.2.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n
个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
- 二叉树是由节点和边构成的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点,没有子节点的节点称为叶子节点。
- 二叉树有一个根节点,其它节点都是根节点的子节点。根节点没有父节点。
- 对于一个有n个节点的二叉树,设其高度为h,则h的取值范围为1到n,且h为log2(n+1)向上取整。
- 在二叉树的第i层上,最多有2^(i-1)个节点。
- 若深度为h的二叉树满足:每个节点都有两个子节点,且所有叶子节点都在第h层或h-1层,则称该树为满二叉树。满二叉树的节点数为2^h-1。
- 若深度为h的二叉树最后一层只有叶子节点,其它层都是满的,则称该树为完全二叉树。完全二叉树的节点数在1到2^(h-1)之间。
- 若二叉树的左右子树可以交换位置且仍为同一棵树,则该二叉树为镜像二叉树。1. 二叉树是由节点和边构成的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点,没有子节点的节点称为叶子节点。
《一些练习的题》
1.某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
答案:
1.B
2.A
3.B
4.B
3. 二叉树的遍历
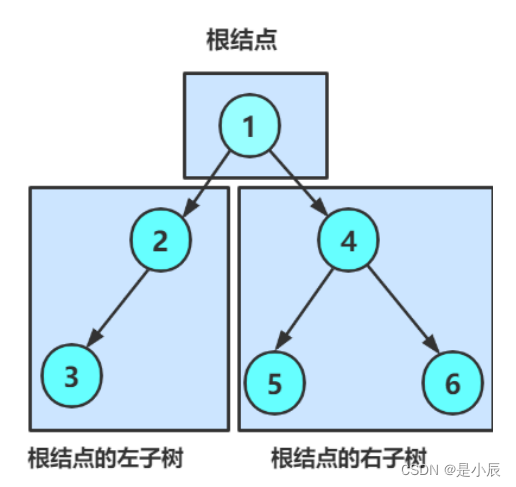
二叉树的遍历是一个重要的点,是一个必须要掌握的点,遍历分为前中后序遍历,层序遍历四种。我们将使用这张图详细介绍一下。
遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
3.1 前序遍历
前序遍历的遍历顺序:访问根结点—>根的左子树—>根的右子树。
遍历结果:123456
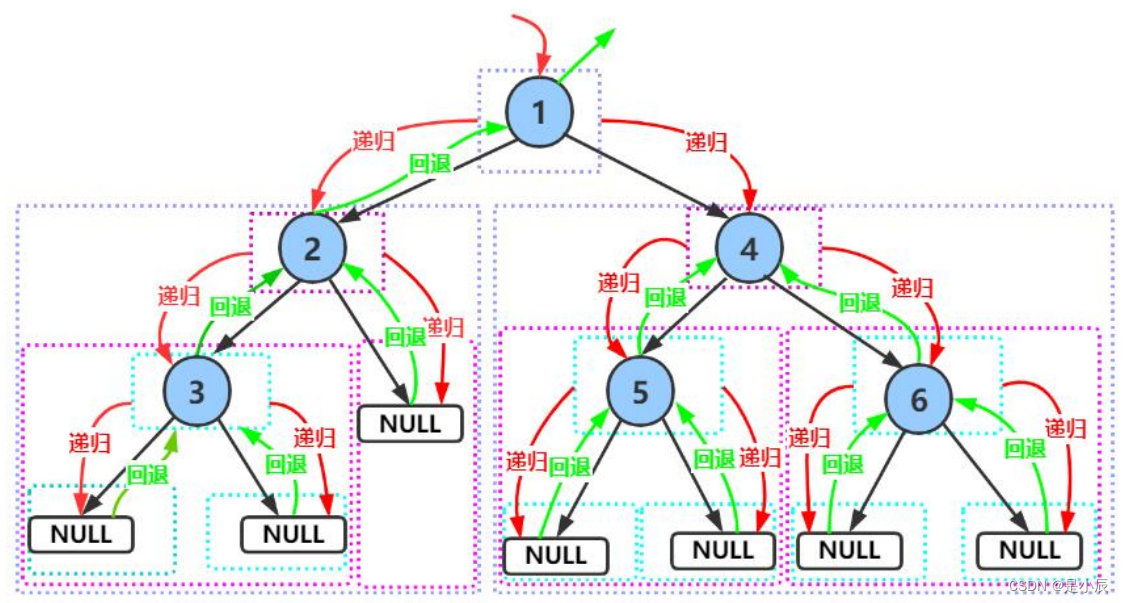
如上图:遍历根节点1,然后遍历左子树2,一直遍历到左子树为null。然后返回途中遍历右子树,3的右子树为null。然后返回到2,2的右子树为null,返回到根节点1。1的左树已经遍历一遍,所以继续遍历1的右子树4,然后先遍历左子树5,5的左右都为空,则返回遍历4的右子树6。6的左右都为空,原路返回,到根节点遍历结束。
3.2 中序遍历
根的左子树—>根节点—>根的右子树。
遍历结果:321546
3.3 后序遍历
根的左子树—>根的右子树—>根节点。
遍历结果:325641
3.4 层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
遍历结果:124356
一些练习选择题
- 某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA- 二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H- 设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde- 某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
【参考答案】 1. A 2. A 3. D 4. A
总结
这篇博客主要为大家带来树及二叉树的基本概念,性质,遍历方式等,下篇博客将为大家带来代码的实现以及应用。
期待大家关注!
最后,祝大家61快乐,天天开心!
相关文章:

二叉树详解:带你掌握二叉树
目录 前言1. 树型结构1. 1 树的概念1.2 树的特点1.3 树的相关术语 2. 二叉树(binary tree)2.1 二叉树的概念2.2 二叉树中的特殊树2.2.1 满二叉树2.2.2 完全二叉树 2.3 二叉树的性质 3. 二叉树的遍历3.1 前序遍历3.2 中序遍历3.3 后序遍历3.4 层序遍历 总…...
LNMP网站框架搭建(编译安装)
目录 一、Nginx的工作原理 工作进程: 二、Nginx编译安装安装 三、mysql的编译安装 四、php的编译安装 验证PHP与nginx的是否连接 验证lnmp的是否搭建成功 五、部署 Discuz!社区论坛 一、Nginx的工作原理 php-fpm.conf 是控制php-fpm守护…...
详解Servlet API
目录 前言 HttpServlet HttpServletRequest 代码实例 打印请求信息 通过URL中的queryString进行传递。 通过post请求的body,使用form表单传递 通过POST 请求中的 body 按照 JSON 的格式进行传递 HttpServletResponse 核心方法代码实例 设置状态码 自动刷…...
【小白教程】Docker安装使用教程,以及常用命令!
【小白教程】Docker安装使用教程,以及常用命令! - 带你薅羊毛最近调试Docker内容,顺手记录一下,我常用的几个命令!这里总结一下,方便自己也同时方便大家使用! 内容慢慢完善更新!如有…...

TypeScript基础
TS编译运行 ts不是在终端运行,是一门中间语言,最终编译为js运行。 手动编译 // 1. ts编译为js npm i -g typescript // 查看版本 tsc -v// 2. ts直接运行,主要用来查看是否报错 npm i -g ts-node // 查看版本 ts-node -v1.手动编译ts代码 …...
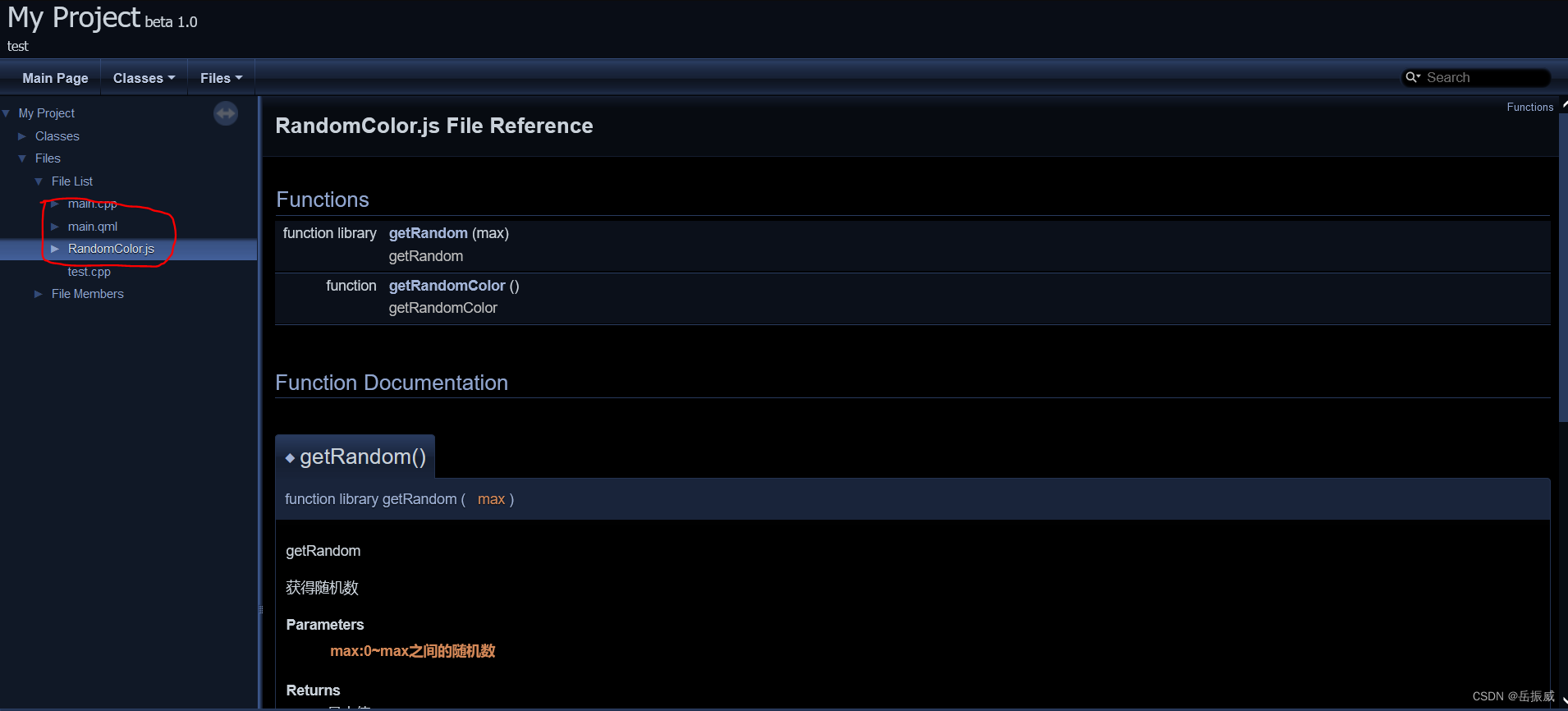
QML学习二:Doxygen为qml工程生成代码文档
效果如下: 设置后能够支持.js和.qml文档。 QML学习二:Doxygen为工程生成注释文档 前言一、安装doxyqml二、Doxygen设置1.文档目录设置2.文档目录设置三、添加注释总结前言 好的代码必须配一个好的文档说明,方便以后维护以及学习。 前提条件: 1.安装好了Doxygen代码生成工…...

Vue 有哪些经典面试题?
前言 下面总结了vue的一些经典的面试题,希望对正在找工作面试的小伙伴们提供一些帮助,我们废话少说直接进入整体、 简述一下什么是MVVM模型 MVVM,是Model-View-ViewModel的简写,其本质是MVC模型的升级版。其中 Model 代表数据模…...
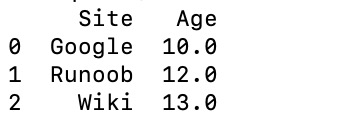
pandas速学-DataFrame
一、理解DataFrame 他是一个表格结构:DataFrame 是一个表格型的数据结构 他是有序的,不同值类型:它含有一组有序的列,每列可以是不同的值类型(数值、字符串、布尔型值)。 他可以被看做一个由series组成的…...

在任务与执行策略之间的隐性耦合
我们已经知道, Executor 框架可以将任务的提交与任务的执行策略解耦开来。就像许多对复杂过程的解耦操作那样,这种论断多少有些言过其实了。虽然Executor 框架为制定和修改执行策略都提供了相当大的灵活性,但并非所有的任务都能适用所有的执行…...

Spring Cloud Alibaba Nacos 构建配置中心
构建配置中心 新建命名空间 登录 Nacos 面板,依次点击左侧菜单栏【命名空间→新建命名空间】、填写命名空间名和描述信息,点击【确定】: 新建配置文件 依次点击左侧菜单栏【配置管理→配置列表】、切换到指定命名空间【此处为 shop】、点击…...

华为OD机试真题 Java 实现【猴子爬山】【2023 B卷 100分】,附详细解题思路
一、题目描述 一天一只顽猴想去从山脚爬到山顶,途中经过一个有个N个台阶的阶梯,但是这猴子有一个习惯: 每一次只能跳1步或跳3步,试问猴子通过这个阶梯有多少种不同的跳跃方式? 二、输入描述 输入只有一个整数N(0<N<=50)此阶梯有多少个阶梯。 三、输出描述 输…...

【19JavaScript for 循环】JavaScript for 循环:掌握重复执行的关键
JavaScript for 循环 在JavaScript中,for循环是一种常用的循环结构,它允许您重复执行一段代码,达到循环的目的。 基本语法 for (initialization; condition; iteration) {// 要执行的代码}for循环由以下几个关键部分组成: init…...
MySQL学习(联结,组合查询,全文本搜索)
联结 SQL最强大的功能之一就是能在数据检索查询的执行中联结表; 关系表 为什么要使用关系表? 使用关系表可以储存数据不重复,从而不浪费时间和空间;如果有数据信息变动,只需更新一个表中的单个记录,相关…...

Nautilus Chain:独特且纯粹的创新型 Layer3
以 Layer3 架构为主要特点的模块化公链 Nautilus Chain 即将在近期上线主网,这也进一步引发了行业关于 Layer3 的讨论。 实际上,在2022年以太坊的创始人 Vitalik 提出了三大目标:Layer2 用于扩展,Layer3 用于定制功能,…...

十六、立方体贴图(天空盒)
第一部分 概念: 1) 引用 OpenGL ES 立方体贴图本质上还是纹理映射,是一种 3D 纹理映射。立方体贴图所使的纹理称为立方图纹理,它是由 6 个单独的 2D 纹理组成,每个 2D 纹理是立方图的一个面。 立方图纹理的采样通过一个 3D 向量…...

UniAD:实现多类别异常检测的统一模型
来源:投稿 作者:Mr.Eraser 编辑:学姐 论文标题:用于多类异常检测的统一模型 论文链接:https://arxiv.org/abs/2206.03687 论文贡献: 提出UniAD,它以一个统一框架完成了多个类别的异常检测。 …...
)
Java 面试 | tcp ip http https(2023版)
文章目录 HTTP&HTTPS1、Http和Https的区别?2、什么是对称加密与非对称加密3、客户端不断进行请求链接会怎样?DDos(Distributed Denial of Service)攻击?4、GET 与 POST 的区别?5、什么是 HTTP 协议无状态协议?怎么解决Http协议无状态协议?6、Session、Cookie 与 Appl…...
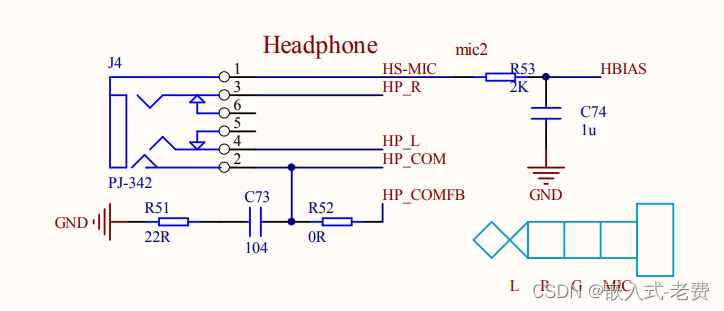
全志V3S嵌入式驱动开发(音频输出和音频录制)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 之前在芯片公司的时候,基本没有看过音频这一块,只知道有个alsa框架这么个知识点。要驱动音频,需要两部分&#…...

使用RP2040自制的树莓派pico—— [2/100] HelloWorld! 和 点亮LED
使用RP2040自制的树莓派pico—— [2/100] HelloWorld! 和 点亮LED 开发环境HelloWorld!闪烁 LED 灯代码 由于比较简单就放在一起写了 开发环境 软件:Thonny HelloWorld! 要想使串口打印HelloWorld! 只需要一行代码 print("HelloWorld!")保…...
康耐视In-Sight2800相机的使用
In-Sight2800相机注册分类程序 一、登录相机 二、图像导入 IS相机支持拍摄图像和从文件中导入图像 如选择从文件中导入图像,文件夹选择位置在页面左下方,如下图 三、注册分类器 在检查模块注册分类器,注册图像需要一张一张去学习&#x…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...