2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
目录
- 2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
- 1、A
- 2、Bx
- 3、Cut
- 4、Diff
- 5、EchoN
- 6、Farmer
- 7、GcdGame
- 8、HouseSub
- 9、IMissYou!
- 10、Jargonless
2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
1、A
题目描述
有一个长为n(1≤n≤1000) 的序列,序列上的元素两两不同。你需要用最少的操作步数翻转这个序列。
每次操作你需要给出三个数 i,j,k(1≤i≤j<k≤n),交换序列中下标属于 [[i,j] 的元素与下标属于[j+1,k] 的元素。例如:对于长为 7 的序列 1,2,3,4,5,6,7,进行操作i=2,j=4,k=6 后序列会变为 1,5,6,2,3,4,7。
给定 n,你需要输出最少的操作步数,并输出每一步的具体操作。保证对于所有输入的 n,均存在至少一个有限步内的合法操作。
输入
一行,一个整数 n。
3
输出
2
1 1 3
1 1 2
第一行一个非负整数 m,表示最少的操作步数。
接下来 m 行,每行三个整数 i,j,k,表示进行题目中描述的操作。
要求 1≤i,j,k≤n,i≤j<k。
你的输出必须保证从上到下执行这 m* 次操作后,整个序列被翻转。
代码
#todo
2、Bx
题目描述
你有一个长度为 n (2≤n≤106) 的 01 序列,你可以执行如下操作若干遍:
每次操作可以选择一个正整数 i,满足 1≤i≤n−k+1,然后选中[i,i+k−1] 这个长度为k (2≤k≤n) 的区间,设这个区间当前的数的最大值为 x*,然后将这个区间中所有的数变成 x。
一个操作序列 i1,i2,⋯,im 是好的当且仅当依次进行这些操作后,整个序列的数都变成 1。
你需要给出一个好的操作序列,使得这个操作序列的长度最小,且满足此情况下,操作序列的字典序最小。
输入
第一行一个整数 T(1≤T≤105),表示数据组数。
对于每组数据:第一行两个整数n,k。
第二行一个长度为 n 的01字符串,表示这个序列。数据保证序列中至少有一个 1和一个 0。
数据保证 ∑n≤106。
2
5 3
00010
6 4
100001
输出
2
3 1
2
1 2
对于每组数据,输出两行:第一行一个整数 m,表示最短的操作次数。
第二行 m 个整数,表示这个操作序列,中间用空格分隔开。
代码
#todo
3、Cut
题目描述
我们可以对数字进行一些有趣的游戏,比如,把数字全部切开又能变成多少?
你现在随意地写下了一个数字n (1≤n<1010),你现在可以任意多次从任意位置切开这个数字,随后将切开的数字加起来,得到一个结果。
你现在想知道所有可能的切法结果的和是多少。
输入
输入一行一个整数 n,表示一开始写下的数字。
125
输出
176
对于样例给出的数字 125,有以下几种切法的可能:
- 125
- 1+25=26
- 12+5=17
- 1+2+5=8
故算式结果的和为 125+26+17+8=176。
代码
s = input()li = []
lis = []
#简单的回溯
def dfs(s):if len(s) < 1:lis.append(li.copy())returnif len(s) == 1:li.append(s)lis.append(li.copy())li.pop()returnfor i in range(1, len(s)+1):li.append(s[0:i])dfs(s[i:len(s)])li.pop()dfs(s)
res = 0
for i in lis:for j in i:res += int(j)
print(res)
4、Diff
题目描述
作为一个居家小能手,你深知收纳之道。
至少,同一种东西不要放在一起,因为同样的东西放在一起容易分不出来……。
现在有n (1≤n≤1000) 个盒子,你现在有 k (2≤k≤1000) 种物品,每种物品的数量有无限个。你现在要在每个盒子里都放一个物品,同时,你不想相邻的位置上摆同样的东西。
想请问有多少种摆放方式可以满足你的要求。
输入
输入一行两个整数 n、k,表示盒子的数量和物品种类的数量。
3 2
输出
2
输出一行一个整数,表示方案数,数据保证答案在 int 范围内。
代码
n, m = map(int, input().split())#简单的数学问题
res = 1
res *= m
for i in range(n-1):res *= (m-1)print(res)
5、EchoN
题目描述
人类的本质是复读机,就是说,人类,人类的本质,是一些东西……人类的本质是什么?人类的本质是复读,人类的本质是复读机。
给定一个字符串 S (∣S∣⩽106),如果其中某一个子串是 S 的前缀,那么我们就说存在一次复读。
想请问一共有多少次复读。
输入
一行一个字符串 S。
aaba
输出
6
一行一个整数,表示复读次数。
代码
s = input()res = len(s)
for i in range(1, len(s)):start = 0while i<=len(s)-1 and s[i] == s[start]:res += 1i += 1start += 1
print(res)
6、Farmer
题目描述
不同的人对于不同的教育方法的接受程度是不一样的,不同的树对于不同的肥料的吸收程度也是不一样的。路边现在种着一排的树,作为新时代新青年的你当然有义务来做些什么,你的手里提着各式各样的化肥。“怎么样才能够成为一个优秀的农民呢?”年纪轻轻的你已经立下了成为农民的远大志向。“这些树,要好好施肥才能茁壮成长啊。”
路边有 n (2⩽n⩽5×103) 棵树,编号从 1 到 n,其中第 i 棵树和第 i+1 棵树之间的距离是 Ai (1⩽Ai⩽109)。现在手上有 m (1⩽m⩽200) 袋肥料,对第 i棵树使用第 j 袋肥料可以获得 Bi,j(1⩽ Bi,j⩽109) 的收益。每一袋肥料只能用在一棵树上,但是一棵树可以用很多袋肥料。
现在定义满意度为得到的收益减去走过的距离,即 ∑B−∑A,如果你可以从任何一棵树开始走,请问你能得到的最大满意度为多少?
需要注意:
1. 你可以按照任意顺序使用化肥,可以先某棵树使用第1、3、5袋化肥,再前往另一棵树使用第2、4袋化肥
2. 你可以在树与树之间任意走动,即可任意往返
输入
第一行两个整数 n、m,表示树的数量和肥料的数量。
接下来一行n−1 个整数 A1,A2,…An−1,表示树之间的距离。
接下来 n行,每行 m 个整数Bij,表示每袋肥料的收益。
3 4
1 4
2 2 5 1
1 3 3 2
2 2 5 1
输出
11
输出一行一个整数,表示最大满意度。
代码
#todo
7、GcdGame
题目描述
有一个长为n (1≤n≤105)的正整数序列,第i个数为ai (2≤ai≤108)。你在这个序列上进行q (1≤q≤105)轮单人游戏,每轮游戏之间相互独立。
在一轮游戏中,你有两个棋子,初始放在序列的第x个位置和第y个位置(1≤x,y≤n);棋子有权值,初始分别为ax和ay。你的目标是让这两个棋子上的权值不互质。每一步,你可以选择一枚棋子,将其移动到序列上相邻的一个位置,即从第i个位置移动到第i−1或第i+1个位置,同时这个棋子上的权值会乘上ai−1或ai+1。注意,第1个位置只能移动到第2个位置,第n个位置只能移动到第n−1个位置。
对于这q轮游戏,请输出每轮游戏达成目标的最小操作步数。
输入
第一行,两个正整数n,q,分别表示序列长度和询问次数。
第二行,n个正整数,第i个数表示ai的值。
接下来q行,每行两个正整数x,y,表示一轮游戏的初始状态。
6 4
2 9 5 7 4 3
4 1
2 6
3 4
5 2
输出
1
0
1
1
q行,每行一个整数,第i行的整数表示第i次询问的答案。
代码
#todo
8、HouseSub
题目描述
一个图称之为“房子”当且仅当这个图是这样的:
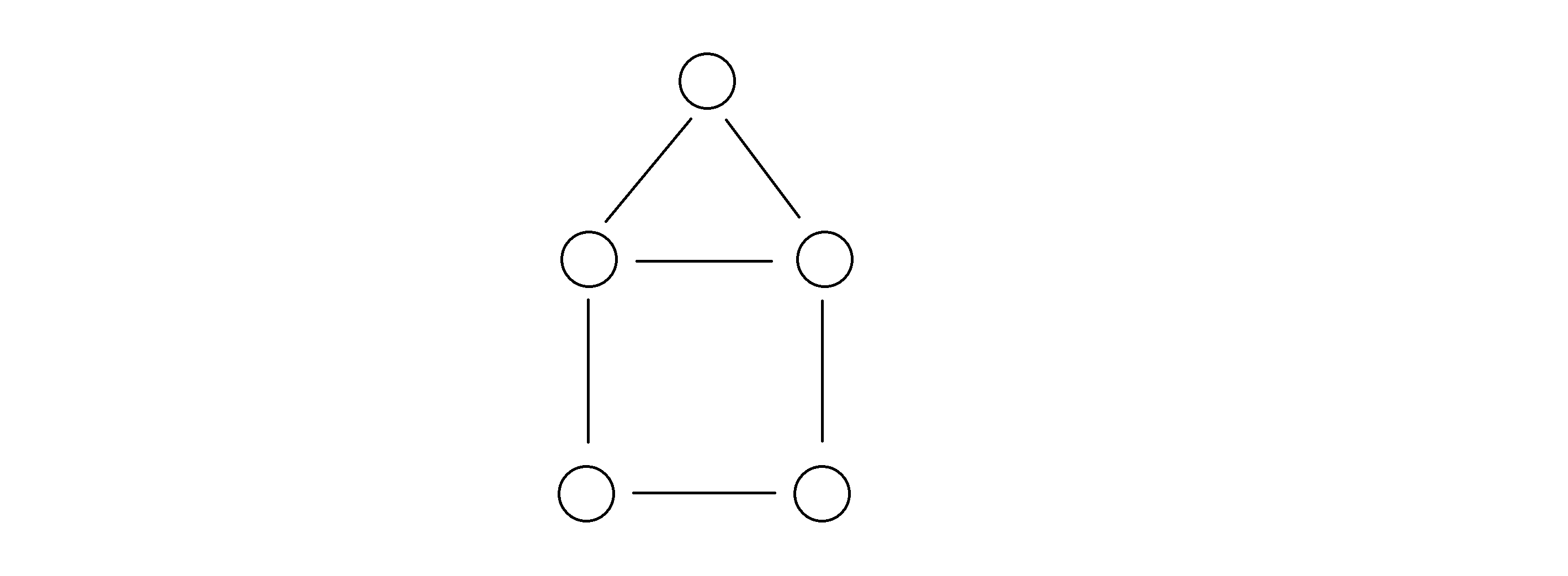
有一个 n (5≤n≤105) 个点 m (5≤m≤105) 条边的无向图,小L想找到 5 个不同的点,并满足这 5 个点能构成一个房子。但对于这 5 个点,下方的四元环必须是“纯四元环”。也就是说,不能出现以下几种情况:
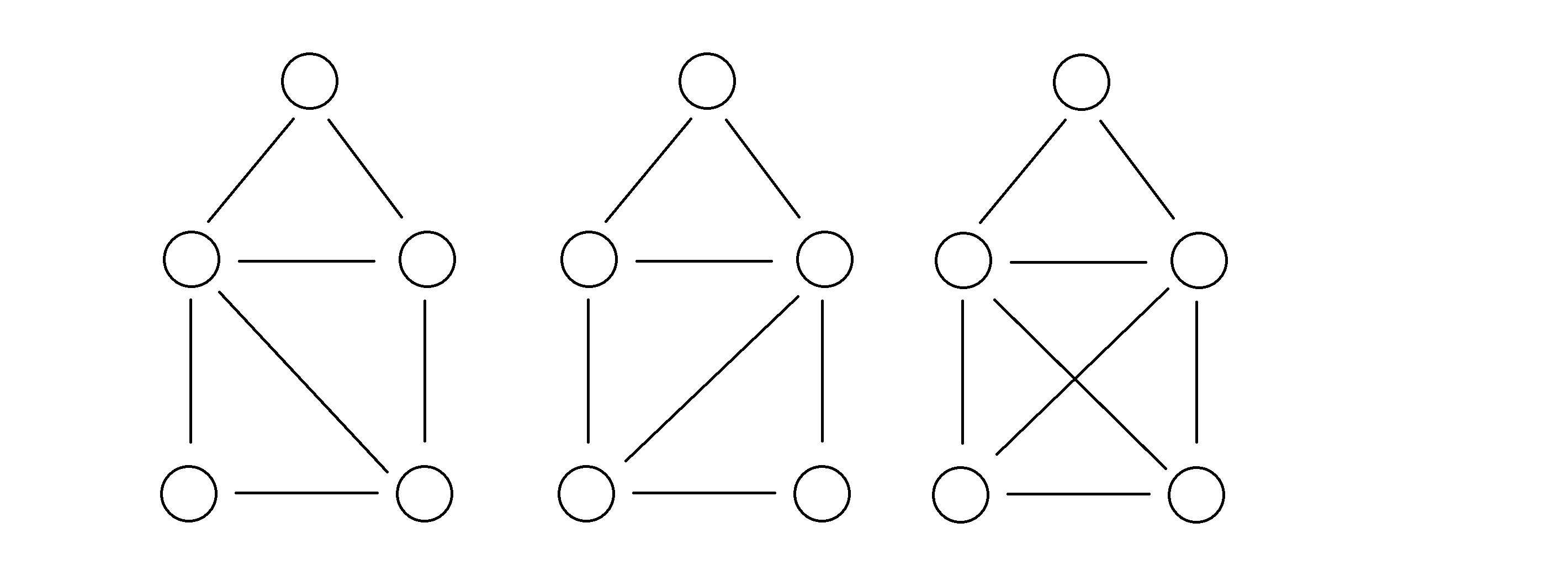
需要注意的是,以下情况是合法的,因为下方的四元环不相邻的两个点对间没有边相连:
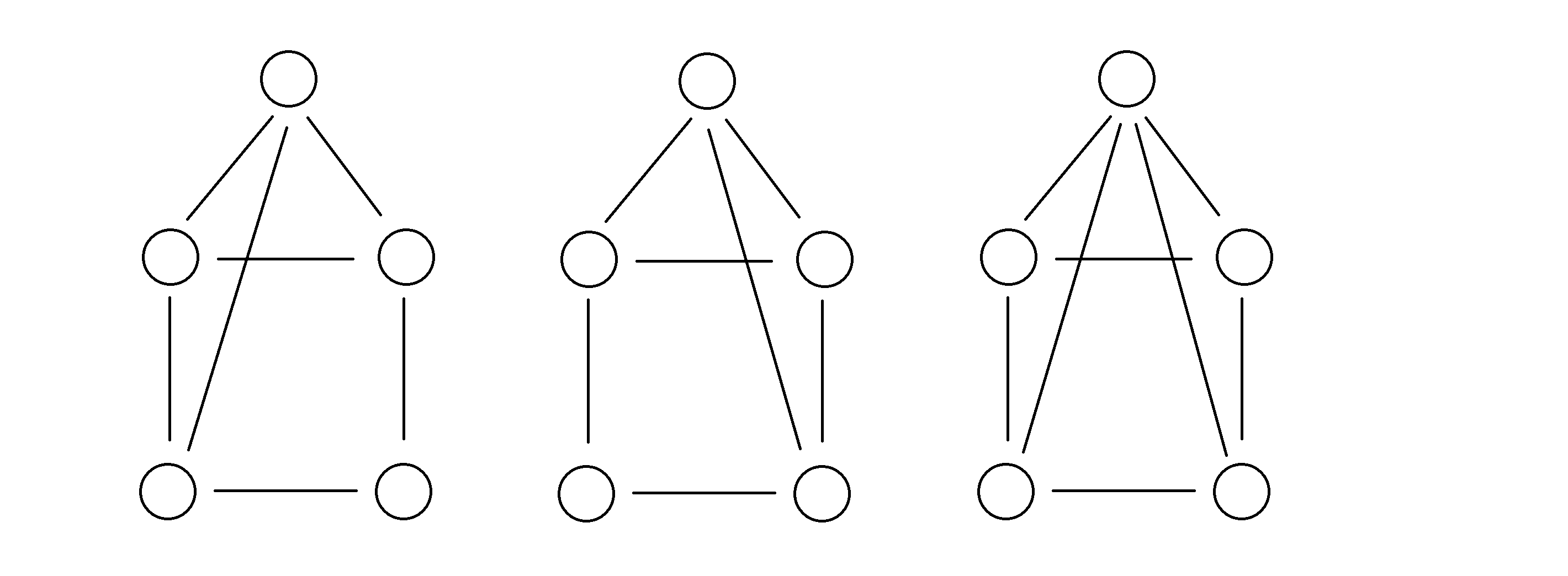
具体地,设这 5 个互不相同的点为u1,u2,u3,u4,u5,小L 想找到满足 u1<u2 且(u1,u2),(u1,u3),(u2,u3),(u1,u4),(u4,u5),(u5,u2) 间有边相连,但 (u1,u5) 和(u2,u4) 间不存在边相连的,(u1,u2,u3,u4,u5) 五元组的方案数。
输入
第一行一个整数 T,表示数据组数。
对于每组数据:第一行两个整数n,m ,表示无向图的点数和边数。
第2∼(m+1) 行,每行两个整数 x,y(1≤x,y≤n,x!=y),表示无向图中的一条边。
保证无向图不存在重边或自环。保证 1≤∑n,∑m≤105。
5 6
1 2
1 3
2 3
1 4
4 5
2 5
输出
1
一行一个整数,表示方案数对 998244353998244353 取模后的结果。
代码
#todo
9、IMissYou!
题目描述
作为一个离家千里的大学生,夜深时你总会思念你的家人。
为了科学研究深夜思念的规律,你记录了这一周内每天的思念值ai (∣ai∣≤100),你想知道这一周内你有多思念家人。如果你的思念值之和严格大于0,则代表思念家人,反之则不思念。
在思念时请输出’IMissYou!‘,并给出总思念值,反之则单独输出’OvO’。(输出时均不包含单引号)。
输入
第一行七个正整数 ai,意义如上所述。
5 5 5 5 5 -2 -2
输出
IMissYou!
21
一行或两行,表示答案。
代码
li = input().split()sum1 = 0
for i in li:sum1 += int(i)if sum1 > 0:print('IMissYou!')print(sum1)
else:print('OvO')
10、Jargonless
题目描述
很多人一些话翻来覆去说得没有任何营养,有用信息就一点点……如果可以不用废话文学,请不要使用废话文学。
给定一个原始文本字符串 S (∣S∣≤3×105) 和一个有用信息字符串 T (∣T∣≤200),现在可以对 S 进行精简操作,具体来说,就是可以将 S 的开头和结尾分别去掉一段,使得剩下的字符串 ′S′ 中包含有有用信息 T*。
请问有多少种精简 S 的方式?
注意:′S′包含T指的是T*是′S′的子序列,如’aacbac’包含’abc’。
输入
第一行一个字符串 S*,表示原始的文本。
第二行一个字符串 T*,表示有用的信息。
abcabcabc
cba
输出
9
输出一行一个整数,表示精简 S 的方案数。
代码
s = input()
t = input()def conTains(s, t):index1 = 0for i in s:if index1 <len(t) and t[index1] == i:index1 += 1if index1 == len(t):return Trueelse:return Falseres = 0
l = 0
r = 0while conTains(s[l:], t):r = 1res += 1while conTains(s[l:len(s) - r], t):# print(f'left:{l}, right:{r}')res += 1r += 1l += 1print(res)
相关文章:

2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
目录 2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)1、A2、Bx3、Cut4、Diff5、EchoN6、Farmer7、GcdGame8、HouseSub9、IMissYou!10、Jargonless 2023年度第四届全国大学生算法设计与编程挑战赛(春季赛) 1、A 题目描述…...

如何用PHP获取各大电商平台的数据
PHP获取API数据是指使用PHP语言从web服务中提取数据。API是指应用程序接口,它允许应用程序之间进行交互和通信,并且允许一个应用程序从另一个应用程序获取数据。PHP是一种网站开发语言,它可以使用多种方式来获取API数据。 在PHP中࿰…...
一站式完成车牌识别任务:从模型优化到端侧部署
交通领域的应用智能化不断往纵深发展,其中最为成熟的车牌识别早已融入人们的日常生活之中,在高速公路电子收费系统、停车场等场景中随处可见。一些企业在具体业务中倾向采用开源方案降低研发成本,但现有公开的方案中少有完成端到端的车牌应用…...
Linux4.8Nginx Rewrite
文章目录 计算机系统5G云计算第六章 LINUX Nginx Rewrite一、Nginx Rewrite 概述1.常用的Nginx 正则表达式2.rewrite和location3.location4.实际网站使用中,至少有三个匹配规则定义5.rewrite6.rewrite 示例 计算机系统 5G云计算 第六章 LINUX Nginx Rewrite 一、…...
DHT11温湿度传感器
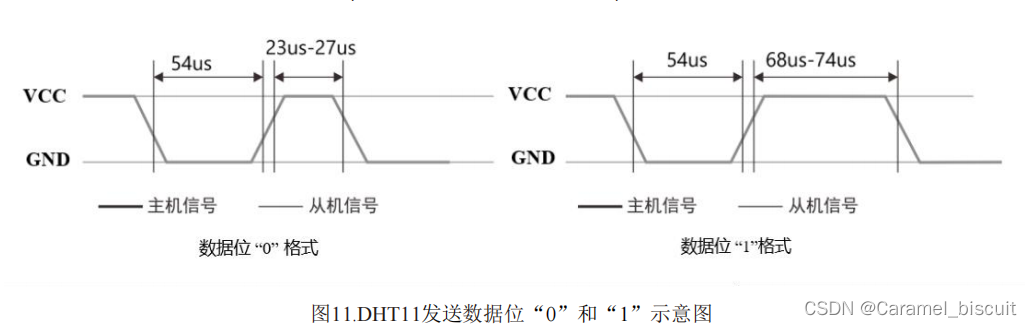
接口定义 传感器通信 DHT11采用简化的单总线通信。单总线仅有一根数据线(SDA),通信所进行的数据交换、挂在单总线上的所有设备之间进行信号交换与传递均在一条通讯线上实现。 单总线上必须有一个上拉电阻(Rp)以实现单…...

RestTemplate超简单上手
目录 1.什么是RestTemplate? 2.RestTemplate的使用 2.1spring环境下 注意1:RestTemplate中发送请求execute()和exchange()方法的区别 execute()方式 exchange()方式 二者的区别 注意2:进阶配置——底层HTTP客户端 2.2非spring环境下 1.什么是R…...

监控系统设计原则及实现目标
1.1.1.1 1 .完善的设计理念: 包括符合国际发展潮流的特性化设计,完整的安防监控及围墙周界报警系统 的布线、设备安装、调试、测试、验收的“交钥匙”工程管理制度,以及符合标 准的质量控制体系。 1.1.1.2 设计原则…...

VulnHub项目:MONEYHEIST: CATCH US IF YOU CAN
靶机名称: MONEYHEIST: CATCH US IF YOU CAN 地址:MoneyHeist: Catch Us If You Can ~ VulnHub 这个系列是一部剧改编,还是挺好看的,大家有兴趣可以去看看! 废话不多说,直接上图开始! 渗透…...

对象存储OSS简介,一分钟了解对象存储OSS
对象存储(Object Storage)是一种新兴的数据存储方式,与传统的文件系统和块存储不同,对象存储以对象为基本单位进行数据管理和存储。在对象存储中,每个对象都有唯一的标识符,并包含了数据本身以及与之相关的…...

SpringCloud_微服务基础day2(Eureka简介与依赖导入,服务注册与发现)
p6:Eureka简介与依赖导入 前面我们了解了如何对单体应用进行拆分,并且也学习了如何进行服务之间的相互调用,但是存在一个问题,就是虽然服务拆分完成,但是没有一个比较合理的管理机制,如果单纯只是这样编写,…...

#tmux# #终端# 常用工具tmux
tmux tmux是一个终端复用工具,允许用户在一个终端会话中同时管理多个终端窗口,提高了终端使用效率,尤其在服务器上进行远程管理时更加实用。在tmux中,可以创建多个终端窗口和窗格,并在这些窗口和窗格之间自由切换&…...

后端服务架构高性能设计之道
“N 高 N 可”,高性能、高并发、高可用、高可靠、可扩展、可维护、可用性等是后台开发耳熟能详的词了,它们中有些词在大部分情况下表达相近意思。本序列文章旨在探讨和总结后台架构设计中常用的技术和方法,并归纳成一套方法论。 前言 本文主…...

Python中的Time和DateTime
Python在处理与时间相关的操作时有两个重要模块:time和datetime。在本文中,我们介绍这两个模块并为每个场景提供带有代码和输出的说明性示例。 time模块主要用于处理时间相关的操作,例如获取当前时间、时间的计算和格式化等。它提供了一些函数…...

UNIX网络编程卷一 学习笔记 第十九章 密钥管理套接字
随着IP安全体系结构(IPsec)的引入,密钥加密和认证密钥的管理越来越需要一套标准机制。RFC 2367介绍了一个通用密钥管理API,可用于IPsec和其他网络安全服务,该API创建了一个新协议族,即PF_KEY域,…...

excel如何实现识别文本在对应单元格填上数据?
要实现 Excel 识别文本在对应单元格填上数据,有以下两种方法: 方法一:使用 VLOOKUP 函数 1. 在 Excel 工作表中,输入一个表格,列名为对应的文本,行名为不同条目。 2. 准备输入数据,在一个新的…...

Groovy 基本语法
一、简介 类型转换:当需要时,类型之间会自动发生类型转换: 字符串(String)、基本类型(如int) 和类型的包装类(如Integer) 类说明:如果在一个groovy 文件中没有任何类定义,它将被当做script 来处理,也就意味着这个文件将…...

系统学习IT技术的方法与实践
系统学习IT技术的方法与实践 作为一名技术人员,在学习新的IT技术时,采取系统性的学习方法是至关重要的。这样可以帮助我们更好地理解和掌握技术,并提高学习效率。下面我将分享一些我个人在系统学习IT技术方面的方法和实践。 1. 设定明确的学…...

聊聊TCP协议的粘包、拆包以及http是如何解决的?
目录 一、粘包与拆包是什么? 二、粘包与拆包为什么发生? 三、遇到粘包、拆包怎么办? 解决方案1:固定数据大小 解决方案2:自定义请求协议 解决方案3:特殊字符结尾 四、HTTP如何解决粘包问题的…...
一百二十、Kettle——用kettle把Hive数据同步到ClickHouse
一、目标 用kettle把hive数据同步到clickhouse,简单运行、直接全量导入数据 工具版本:kettle:8.2 Hive:3.1.2 ClickHouse21.9.5.16 二、前提 (一)kettle连上hive (二)kettle连上cli…...

PyTorch 提示和技巧:从张量到神经网络
张量和梯度 我们将深入探讨使用 PyTorch 构建自己的神经网络必须了解的 2 个基本概念:张量和梯度。 张量 张量是 PyTorch 中的中央数据单元。它们是类似于数组的数据结构,在功能和属性方面与 Numpy 数组非常相似。它们之间最重要的区别是 PyTorch 张量…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
