机器学习 | 降维问题
目录
一、主成分分析
二、奇异值分解
2.1 奇异值分解原理
2.2 奇异值分解实践
三、特征值与特征向量
一、主成分分析
主成分有如下特征:
- 每个主成分是原变量的线性组合;
- 各个主成分之间互不相关;
- 主成分按照方差贡献率从大到小依次排列;
- 所有主成分的方差贡献率求和为1;
- 提取后的主成分通常小于原始数据变量的数量;
- 提取后的主成分尽可能地保留了原始变量中的大部分信息。
我们仍以经典的鸢尾花数据集对主成分分析进行介绍。
通过导入PCA进行主成分分析。
#导入库
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris#导入数据
data=load_iris()#主成分分析
model=PCA()
model.fit(data.data)#显示主成分信息
pd.DataFrame(model.transform(data.data),columns=["PC{}".format(x+1) for x in range(data.data.shape[1])])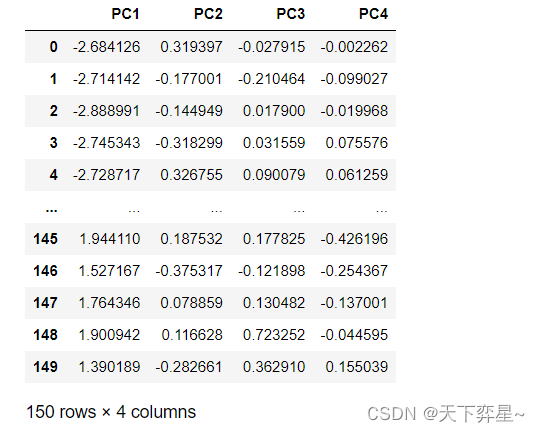
上述结果给出了鸢尾花数据集的4个(全部)主成分,然而选择几个主成分需要进一步判断。这里可以通过计算主成分的累计贡献率进行判断,代码如下:
import matplotlib.ticker as ticker
import matplotlib.pyplot as plt
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0]+list(np.cumsum(model.explained_variance_ratio_)),"-")
plt.xlabel("Number of principal componets")
plt.ylabel("Cumulative contribution rate")
plt.show()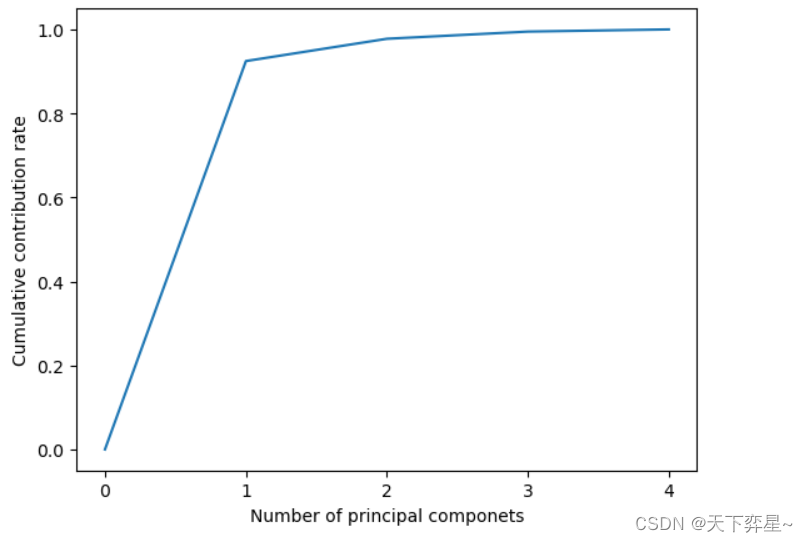
从上图可以看出,主成分从0~1时非常陡峭,而从1往后区域平缓,因此,针对4维鸢尾花数据,我们只需要保留1个主成分,即将原4维数据降维到现在的1维。
利用下面的代码,我们可以用更加量化的方式查看主成分累积贡献率。
model.explained_variance_ratio_![]()
结果显示,1个主成分就已经达到了92.46%,保留了原数据中绝大部分信息。
综上,主成分分析的全部代码如下:
#导入库
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris#导入数据
data=load_iris()#主成分分析
model=PCA()
model.fit(data.data)#显示主成分信息
pd.DataFrame(model.transform(data.data),columns=["PC{}".format(x+1) for x in range(data.data.shape[1])])#绘制主成分的累积贡献率的折线图
import matplotlib.ticker as ticker
import matplotlib.pyplot as plt
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0]+list(np.cumsum(model.explained_variance_ratio_)),"-")
plt.xlabel("Number of principal componets")
plt.ylabel("Cumulative contribution rate")
plt.show()#量化主成分的累计贡献率
model.explained_variance_ratio_二、奇异值分解
2.1 奇异值分解原理
奇异值分解(SVD)将一个任意矩阵进行分解,无须考虑特征值分解时需要矩阵是方阵的前提。
假设矩阵M是一个阶矩阵,则可以将其分解为下面的三个矩阵相乘:
其中:
- U是
阶正交矩阵,
,
为单位矩阵;
是
阶正交矩阵,
;
是
阶非负实数对角矩阵,
。
这种将矩阵M分解的方法就被称为奇异值分解,矩阵上对角线上的元素即为M的奇异值。
考虑一个的任意矩阵,此时
的秩为n,矩阵中不同深度的灰色表示奇异值大小不同,对角线上的奇异值(假设存在n个非零的奇异值)依次从大到小进行排列。在这种情况下,矩阵U的最后m-n列失去了意义。
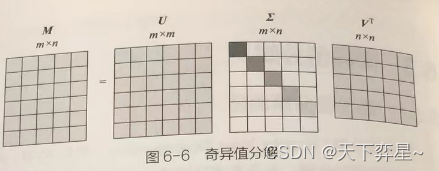
因此可以做进一步的变化,此时阶的矩阵U变为
阶的矩阵
,
阶的矩阵
变为
阶的矩阵
。
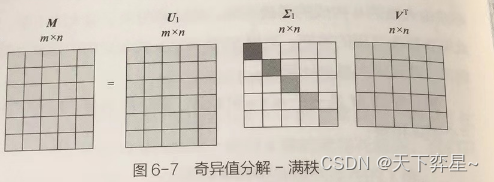
当我们取k<n,比如k=2时,即认为前两个奇异值占总奇异值之和的比例非常大,因此可以如下图进行运算,尽管此时,但是由于删除的奇异值占比很小,我们可以认为
。
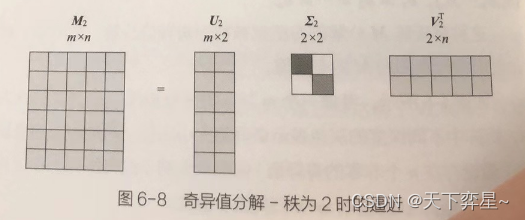
2.2 奇异值分解实践
利用python可以很方便实现对矩阵的奇异值分解,例如对阶的矩阵M进行奇异值分解:
代码如下:
import numpy as np
M=np.array([[1,0,0,0,2],[0,0,3,0,0],[0,0,0,0,0],[0,4,0,0,0]])
U,Sigma,VT=np.linalg.svd(M)
print("U:",U)
print("Sigma:",Sigma)
print("VT:",VT)
导入一张图片,下面的代码给出了地秩近似序列使用奇异值分解逼近的图片。
import numpy as np
import matplotlib.pyplot as plt
from PIL import Imager_max=300 #设置最大的秩
Pic="C:\\Users\\LEGION\\Pictures\\Saved Pictures\\暨大logo.png"image=Image.open(Pic).convert("L")
img_mat=np.asarray(image)U,s,V=np.linalg.svd(img_mat,full_matrices=True)
s=np.diag(s)for k in range(r_max+1):approx=U[:,:k] @ s[0:k,:k] @ V[:k,:]img=plt.imshow(approx,cmap='gray')plt.title("SVD approximation with degree of %d"%(k))plt.plot()plt.pause(0.001)plt.clf()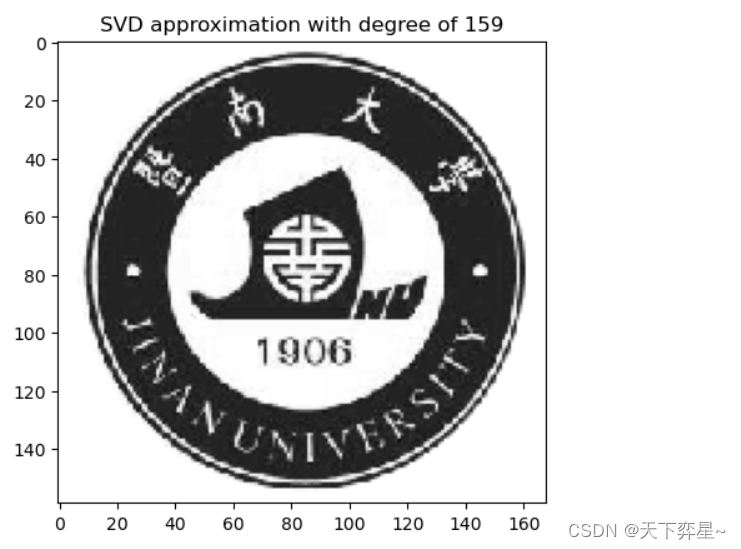
三、特征值与特征向量
利用python与Numpy库,很容易得到一个矩阵的特征值和特征向量。
import numpy as np
A=np.array([[1,2],[3,4]])
a,b=np.linalg.eig(A)
print("A的特征值为:\n",a)
print('A的特征向量为:\n',b) 
通过np.lianlg.eig()函数得到的特征向量是已经标准化的向量, 即长度为1.改函数给出的特征值未按大小顺序排序。
除了特征值和特征向量外,协方差矩阵与相关系数矩阵也是降维分析中的重要概念。以鸢尾花的4个特征向量为例,协方差矩阵的每个元素是各个向量元素之间的协方差,相关系数矩阵的各元素是由各特征间的相关系数构成的。
import numpy as np
from sklearn.datasets import load_iris#导入数
data=load_iris()
X=data.dataCov_X=np.cov(X.T) #求解协方差矩阵
Cor_X=np.corrcoef(X.T) #求解相关系数矩阵print("协方差矩阵:\n",Cov_X)
print("相关系数矩阵:\n",Cor_X)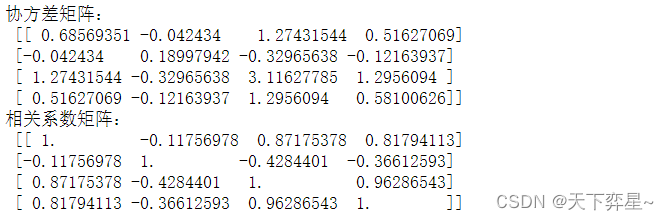
利用协方差矩阵和相关系数矩阵可以求解主成分。这里以利用协方差矩阵为例进行说明。
沿用上面的协方差矩阵数据,可以求得其特征值和特征向量:
import numpy as np
from sklearn.datasets import load_iris#导入数
data=load_iris()
X=data.dataCov_X=np.cov(X.T) #求解协方差矩阵a,b=np.linalg.eig(Cov_X)
print("协方差矩阵的特征值为:\n",a)
print('协方差矩阵的特征向量为:\n',b)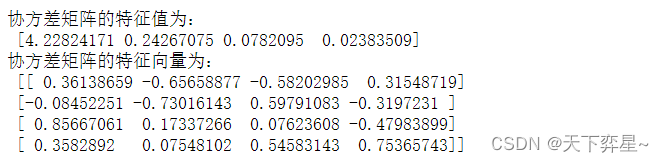
协方差矩阵的特征值即为主成分的方差贡献率:
第一个主成分(解释方差)所占比例已经高达92.46%,说明已经可以在这个比例上解释原始数据信息,因此可以将鸢尾花数据从四维降至一维。第一主成分如下:
其中,表示该列特征的均值,等式右边的系数为协方差矩阵的特征向量的第一列(与第一个特征值相对应的数值)。
除了协方差矩阵,相关系数矩阵也可以求解主成分。但是两种不同的求解方法结果通常会有一定的差别。此外,值得注意的是,如果对已经标准化的数据求协方差矩阵,实际上就是对原变量求相关系数矩阵。
在求解主成分时,如果变量间的单位不同,应该先将变量标准化后进行计算。否则由于单位不同导致的取值范围悬殊太大会影响最终的结果。
相关文章:
机器学习 | 降维问题
目录 一、主成分分析 二、奇异值分解 2.1 奇异值分解原理 2.2 奇异值分解实践 三、特征值与特征向量 一、主成分分析 主成分有如下特征: 每个主成分是原变量的线性组合;各个主成分之间互不相关;主成分按照方差贡献率从大到小依次排列&…...
Ubuntu20.04平台下使用二进制包部署MongoDB-6.0.4单实例
文章目录 1.1 准备服务器的基本信息1.2 操作系统上创建其用户1.3 部署MongoDB服务端1.4 部署MongoDB客户端1.5 部署MongoDB 27017实例1.5.1 创建相关目录1.5.2 准备配置文件1.5.3 准备启停脚本1.5.4 进行启停测试1.5.5 加入开机自启动 1.6 创建超级管理员用户1.6.1 创建本地的超…...
Snipaste工具推荐
Snipaste Snipaste 不只是截图,善用贴图功能将帮助你提升工作效率! 新用户? 截图默认为 F1,贴图为 F3,然后请对照着 快捷键列表 按一遍,体会它们的用法,就入门啦! 遇到了麻烦&…...
MinIO快速入门——在Linux系统上安装和启动
1、简介 MinIO 是一款基于Go语言发开的高性能、分布式的对象存储系统。客户端支持Java,Net,Python,Javacript, Golang语言。MinIO系统,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。 2、环境搭建&#…...
07.JavaWeb-Vue+elementUI
1.Vue 功能替代JavaScript和jQuery,基于JavaScript实现的前端框架 1.1配置Vue 1.1.1引入vue库 方法一:通过cdn链接引入最新版本的vue(可能会慢些) <head><script src"https://cdn.jsdelivr.net/npm/vue">…...
经典面试题---【第一档】
1.如果你想new一个Quene,你有几种方式?他们之间的区别是什么? 2.Redis 是如何判断数据是否过期的呢? Redis 通过一个叫做过期字典(可以看作是 hash 表)来保存数据过期的时间。过期字典的键指向 Redis 数据…...

欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)正式启动,开启报名通道
6月8日,欧美同学会第三届“双创”大赛——空天装备产业赛区(浙江诸暨)启动仪式暨北京推介会圆满举行。活动由欧美同学会(中国留学人员联谊会)主办,中共浙江省委统战部支持,浙江省欧美同学会、中…...

python3 爬虫相关学习8:python 的常见报错内容 汇总收集
目录 1 拼写错误 AttributeError: NameError: 等等 2 类型错误 TypeError: 如字符串连接错误 TypeError: can only concatenate str (not “int“) to str 3 意外缩进 IndentationError: unexpected indent 4 找不到对应模块 ModuleNotFoundError: 5 语法错误 Syntax…...
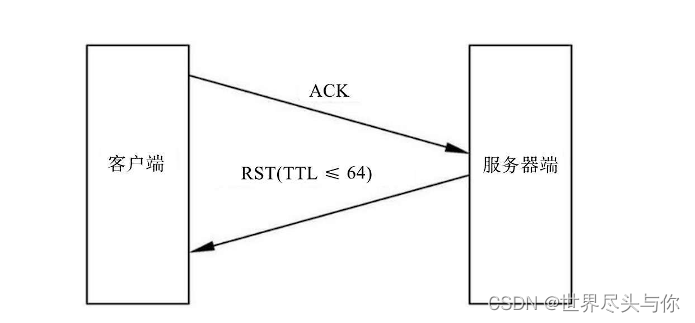
活跃主机发现技术指南
活跃主机发现技术指南 1.活跃主机发现技术简介2.基于ARP协议的活跃主机发现技术3.基于ICMP协议的活跃主机发现技术4.基于TCP协议的活跃主机发现技术5.基于UDP协议的活跃主机发现技术6.基于SCTP协议的活跃主机发现技术7.主机发现技术的分析 1.活跃主机发现技术简介 在生活中有这…...
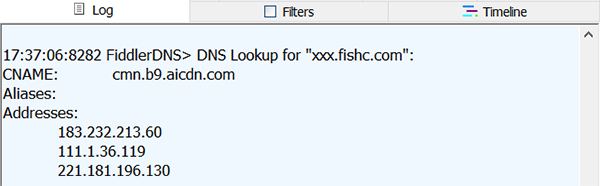
手机抓包fiddler配置及使用教程
本文基于Fiddler4讲解基本使用 fiddler抓包原理 注意:Fiddler 是以代理web服务器的形式工作的,它使用代理地址:127.0.0.1,端口:8888。当Fiddler退出的时候它会自动注销,这样就不会影响别的 程序。不过如果Fiddler非正常退出&…...
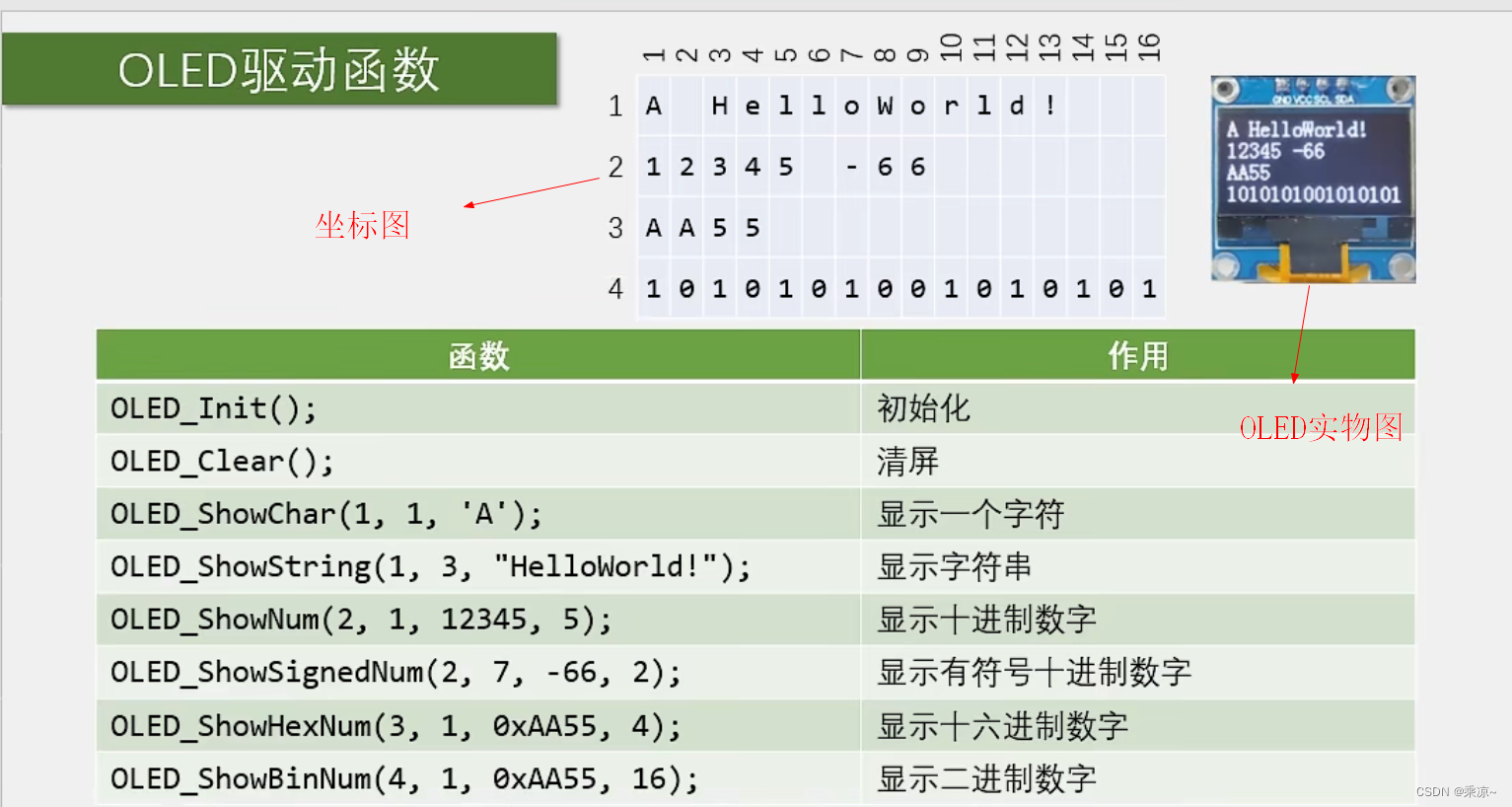
STM32单片机(四)第一节:OLED调试工具
❤️ 专栏简介:本专栏记录了从零学习单片机的过程,其中包括51单片机和STM32单片机两部分;建议先学习51单片机,其是STM32等高级单片机的基础;这样再学习STM32时才能融会贯通。 ☀️ 专栏适用人群 :适用于想要…...

自用的一些网址,码住!
京东羚珑智能抠图网站https://ling.jd.com/live/fm#all:主要用于商品抠图,而且还有多种直播背景设计,非常方便。国外的免费抠图网站https://www.remove.bg/zh/upload:有一个魔法棒的设计,可以自己选择抠图的范围和形状…...

银行vr元宇宙全景虚拟展馆提供更加真实、立体、高效的数字资产交易场景
为了贯彻国家普惠金融政策,使金融如无惠及广大群体,宇宙技术在金融行业中的应用将进一步提升金融消费体验感觉和金融管理水平。打造元宇宙金融服务平台,构建虚实结构的金融服务世界,培育和管理好数字机器人员工队伍,提升金融业务各…...
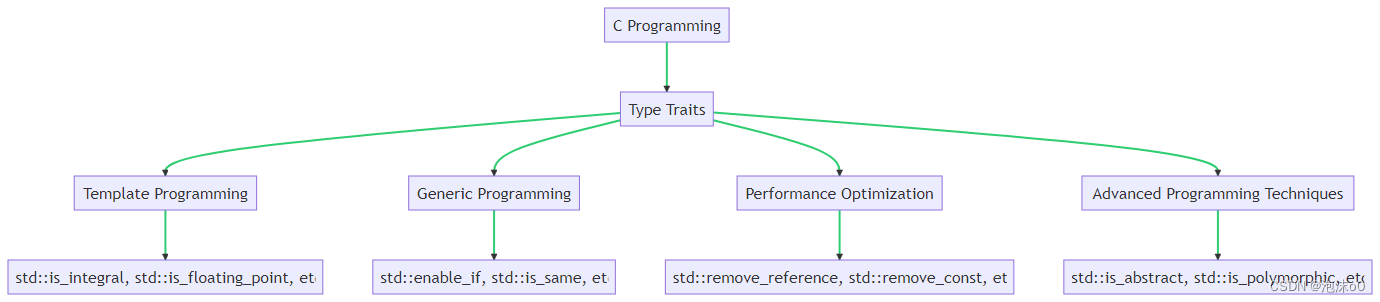
C++ 泛型编程 类型萃取器的运用
C 泛型编程 类型萃取器的运用 一、C类型萃取器的基本概念与应用(Type Traits in C)1.1 类型萃取器的定义与作用(Definition and Role of Type Traits)1.2 类型萃取器的分类与特性(Classification and Characteristics …...
C++ String类(上篇)
绪论 放弃时间的人,时间也会放弃他。——莎士比亚 ; 本篇章是关于string类内一些函数的介绍以及使用方法,都是我们编程必须掌握的基础! 全文共7000字左右. 话不多说安全带系好,发车啦(建议电脑观看&…...

nested exception is java.lang.NoClassDefFoundError
出现这种问题,一般都是jar有问题,排查是哪个jar包,重新导入maven仓库一下就行了,有的时候需要把原来仓库里的包删掉,重新打包,有的时候要切换分支,到其他分支打包。 打包时候没有打进去…...

科普:python怎么使用Pyinstaller模块打包成可执行文件
目录 1. 使用conda创建虚拟环境2. 列出所有虚拟环境查看是否创建成功3. 激活虚拟环境4. 安装Pyinstaller模块5. Pyinstaller模块常用参数6. 例子:Windows打包成单个文件并可使用命令行窗口并自定义文件logo 1. 使用conda创建虚拟环境 创建个虚拟环境来打包…...

企业级应用高性能可扩展架构设计
前言 马上又要618了,每年到了这个时候,商家就开始促销,价格低会吸引来超多用户,对系统来说就是更多的流量,技术上如何确保网站稳定运行,且不被超卖,同时还要让用户有个良好的购物体验。 12306…...

【安全架构】
概念 安全是产品的属性,安全的目标是保障产品里信息资产的保密性(Confidentiality)、完整性(Integrity)和可用性(Availability),简记为CIA。 保密性: 保障信息资产不被未…...
RabbitMq-高级
参考:https://blog.csdn.net/dingd1234/article/details/125032383 1 TTL TTL QUEUE 声明args TTL MESSAGE postmessage中设置 区别:过期消息会直接删除消息,过期队列若配置死信队列会移到死信队列 ps:同时配置两个已小的为准 2…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
